Using Progenitor Strain Information to Identify Quantitative Trait Nucleotides in Outbred Mice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
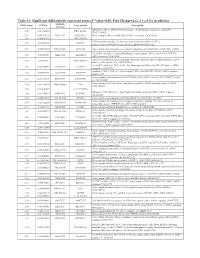
(P -Value<0.05, Fold Change≥1.4), 4 Vs. 0 Gy Irradiation
Table S1: Significant differentially expressed genes (P -Value<0.05, Fold Change≥1.4), 4 vs. 0 Gy irradiation Genbank Fold Change P -Value Gene Symbol Description Accession Q9F8M7_CARHY (Q9F8M7) DTDP-glucose 4,6-dehydratase (Fragment), partial (9%) 6.70 0.017399678 THC2699065 [THC2719287] 5.53 0.003379195 BC013657 BC013657 Homo sapiens cDNA clone IMAGE:4152983, partial cds. [BC013657] 5.10 0.024641735 THC2750781 Ciliary dynein heavy chain 5 (Axonemal beta dynein heavy chain 5) (HL1). 4.07 0.04353262 DNAH5 [Source:Uniprot/SWISSPROT;Acc:Q8TE73] [ENST00000382416] 3.81 0.002855909 NM_145263 SPATA18 Homo sapiens spermatogenesis associated 18 homolog (rat) (SPATA18), mRNA [NM_145263] AA418814 zw01a02.s1 Soares_NhHMPu_S1 Homo sapiens cDNA clone IMAGE:767978 3', 3.69 0.03203913 AA418814 AA418814 mRNA sequence [AA418814] AL356953 leucine-rich repeat-containing G protein-coupled receptor 6 {Homo sapiens} (exp=0; 3.63 0.0277936 THC2705989 wgp=1; cg=0), partial (4%) [THC2752981] AA484677 ne64a07.s1 NCI_CGAP_Alv1 Homo sapiens cDNA clone IMAGE:909012, mRNA 3.63 0.027098073 AA484677 AA484677 sequence [AA484677] oe06h09.s1 NCI_CGAP_Ov2 Homo sapiens cDNA clone IMAGE:1385153, mRNA sequence 3.48 0.04468495 AA837799 AA837799 [AA837799] Homo sapiens hypothetical protein LOC340109, mRNA (cDNA clone IMAGE:5578073), partial 3.27 0.031178378 BC039509 LOC643401 cds. [BC039509] Homo sapiens Fas (TNF receptor superfamily, member 6) (FAS), transcript variant 1, mRNA 3.24 0.022156298 NM_000043 FAS [NM_000043] 3.20 0.021043295 A_32_P125056 BF803942 CM2-CI0135-021100-477-g08 CI0135 Homo sapiens cDNA, mRNA sequence 3.04 0.043389246 BF803942 BF803942 [BF803942] 3.03 0.002430239 NM_015920 RPS27L Homo sapiens ribosomal protein S27-like (RPS27L), mRNA [NM_015920] Homo sapiens tumor necrosis factor receptor superfamily, member 10c, decoy without an 2.98 0.021202829 NM_003841 TNFRSF10C intracellular domain (TNFRSF10C), mRNA [NM_003841] 2.97 0.03243901 AB002384 C6orf32 Homo sapiens mRNA for KIAA0386 gene, partial cds. -

WO 2012/174282 A2 20 December 2012 (20.12.2012) P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2012/174282 A2 20 December 2012 (20.12.2012) P O P C T (51) International Patent Classification: David [US/US]; 13539 N . 95th Way, Scottsdale, AZ C12Q 1/68 (2006.01) 85260 (US). (21) International Application Number: (74) Agent: AKHAVAN, Ramin; Caris Science, Inc., 6655 N . PCT/US20 12/0425 19 Macarthur Blvd., Irving, TX 75039 (US). (22) International Filing Date: (81) Designated States (unless otherwise indicated, for every 14 June 2012 (14.06.2012) kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BR, BW, BY, BZ, English (25) Filing Language: CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, DO, Publication Language: English DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, HN, HR, HU, ID, IL, IN, IS, JP, KE, KG, KM, KN, KP, KR, (30) Priority Data: KZ, LA, LC, LK, LR, LS, LT, LU, LY, MA, MD, ME, 61/497,895 16 June 201 1 (16.06.201 1) US MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, 61/499,138 20 June 201 1 (20.06.201 1) US OM, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SC, SD, 61/501,680 27 June 201 1 (27.06.201 1) u s SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, 61/506,019 8 July 201 1(08.07.201 1) u s TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, ZW. -

35Th International Society for Animal Genetics Conference 7
35th INTERNATIONAL SOCIETY FOR ANIMAL GENETICS CONFERENCE 7. 23.16 – 7.27. 2016 Salt Lake City, Utah ABSTRACT BOOK https://www.asas.org/meetings/isag2016 INVITED SPEAKERS S0100 – S0124 https://www.asas.org/meetings/isag2016 epigenetic modifications, such as DNA methylation, and measuring different proteins and cellular metab- INVITED SPEAKERS: FUNCTIONAL olites. These advancements provide unprecedented ANNOTATION OF ANIMAL opportunities to uncover the genetic architecture GENOMES (FAANG) ASAS-ISAG underlying phenotypic variation. In this context, the JOINT SYMPOSIUM main challenge is to decipher the flow of biological information that lies between the genotypes and phe- notypes under study. In other words, the new challenge S0100 Important lessons from complex genomes. is to integrate multiple sources of molecular infor- T. R. Gingeras* (Cold Spring Harbor Laboratory, mation (i.e., multiple layers of omics data to reveal Functional Genomics, Cold Spring Harbor, NY) the causal biological networks that underlie complex traits). It is important to note that knowledge regarding The ~3 billion base pairs of the human DNA rep- causal relationships among genes and phenotypes can resent a storage devise encoding information for be used to predict the behavior of complex systems, as hundreds of thousands of processes that can go on well as optimize management practices and selection within and outside a human cell. This information is strategies. Here, we describe a multi-step procedure revealed in the RNAs that are composed of 12 billion for inferring causal gene-phenotype networks underly- nucleotides, considering the strandedness and allelic ing complex phenotypes integrating multi-omics data. content of each of the diploid copies of the genome. -

Full-Text.Pdf
Systematic Evaluation of Genes and Genetic Variants Associated with Type 1 Diabetes Susceptibility This information is current as Ramesh Ram, Munish Mehta, Quang T. Nguyen, Irma of September 23, 2021. Larma, Bernhard O. Boehm, Flemming Pociot, Patrick Concannon and Grant Morahan J Immunol 2016; 196:3043-3053; Prepublished online 24 February 2016; doi: 10.4049/jimmunol.1502056 Downloaded from http://www.jimmunol.org/content/196/7/3043 Supplementary http://www.jimmunol.org/content/suppl/2016/02/19/jimmunol.150205 Material 6.DCSupplemental http://www.jimmunol.org/ References This article cites 44 articles, 5 of which you can access for free at: http://www.jimmunol.org/content/196/7/3043.full#ref-list-1 Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision by guest on September 23, 2021 • No Triage! Every submission reviewed by practicing scientists • Fast Publication! 4 weeks from acceptance to publication *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2016 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. The Journal of Immunology Systematic Evaluation of Genes and Genetic Variants Associated with Type 1 Diabetes Susceptibility Ramesh Ram,*,† Munish Mehta,*,† Quang T. -

Variation in Protein Coding Genes Identifies Information Flow
bioRxiv preprint doi: https://doi.org/10.1101/679456; this version posted June 21, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Animal complexity and information flow 1 1 2 3 4 5 Variation in protein coding genes identifies information flow as a contributor to 6 animal complexity 7 8 Jack Dean, Daniela Lopes Cardoso and Colin Sharpe* 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Institute of Biological and Biomedical Sciences 25 School of Biological Science 26 University of Portsmouth, 27 Portsmouth, UK 28 PO16 7YH 29 30 * Author for correspondence 31 [email protected] 32 33 Orcid numbers: 34 DLC: 0000-0003-2683-1745 35 CS: 0000-0002-5022-0840 36 37 38 39 40 41 42 43 44 45 46 47 48 49 Abstract bioRxiv preprint doi: https://doi.org/10.1101/679456; this version posted June 21, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Animal complexity and information flow 2 1 Across the metazoans there is a trend towards greater organismal complexity. How 2 complexity is generated, however, is uncertain. Since C.elegans and humans have 3 approximately the same number of genes, the explanation will depend on how genes are 4 used, rather than their absolute number. -

Content Based Search in Gene Expression Databases and a Meta-Analysis of Host Responses to Infection
Content Based Search in Gene Expression Databases and a Meta-analysis of Host Responses to Infection A Thesis Submitted to the Faculty of Drexel University by Francis X. Bell in partial fulfillment of the requirements for the degree of Doctor of Philosophy November 2015 c Copyright 2015 Francis X. Bell. All Rights Reserved. ii Acknowledgments I would like to acknowledge and thank my advisor, Dr. Ahmet Sacan. Without his advice, support, and patience I would not have been able to accomplish all that I have. I would also like to thank my committee members and the Biomed Faculty that have guided me. I would like to give a special thanks for the members of the bioinformatics lab, in particular the members of the Sacan lab: Rehman Qureshi, Daisy Heng Yang, April Chunyu Zhao, and Yiqian Zhou. Thank you for creating a pleasant and friendly environment in the lab. I give the members of my family my sincerest gratitude for all that they have done for me. I cannot begin to repay my parents for their sacrifices. I am eternally grateful for everything they have done. The support of my sisters and their encouragement gave me the strength to persevere to the end. iii Table of Contents LIST OF TABLES.......................................................................... vii LIST OF FIGURES ........................................................................ xiv ABSTRACT ................................................................................ xvii 1. A BRIEF INTRODUCTION TO GENE EXPRESSION............................. 1 1.1 Central Dogma of Molecular Biology........................................... 1 1.1.1 Basic Transfers .......................................................... 1 1.1.2 Uncommon Transfers ................................................... 3 1.2 Gene Expression ................................................................. 4 1.2.1 Estimating Gene Expression ............................................ 4 1.2.2 DNA Microarrays ...................................................... -

Molecular Signatures of the Pathogenesis ISBN-10: 90-9021312-0 ISBN-13: 978-90-9021312-5
GENOMICS OF COELIAC DISEASE Molecular Signatures of the Pathogenesis ISBN-10: 90-9021312-0 ISBN-13: 978-90-9021312-5 Cover, layout and print: Budde Grafimedia bv, Nieuwegein The work presented in this thesis was performed at the DBG - Department of Medical Genetics of the University Medical Center Utrecht, and financially supported by the Dutch Digestive Disease Foundation (MLDS) grants WS 00-13 and WS 97-44, the Netherlands Organization for Medical and Health Research (NWO) grants 902-22-094 and 912-02-028, and by the Celiac Disease Consortium, an Innovative Cluster approved by the Netherlands Genomics Initiative and partially funded by the Dutch Government (BSIK03009). The publication of this thesis was facilitated by a financial contribution from the Department of Medical Genetics and generous donations from the Dutch Digestive Disease Foundation (MLDS); the Section of Experimental Gastroenterology (SGE) of the Netherlands Society of Gastroenterology (NVGE); the JE Juriaanse Stichting; and the Dr Ir JHJ van der Laar Stichting. GENOMICS OF COELIAC DISEASE Molecular Signatures of the Pathogenesis GENOMICS VAN COELIAKIE Moleculaire Kenmerken van de Pathogenese (met een inleiding en samenvatting in het Nederlands) Proefschrift ter verkrijging van de graad van doctor aan de Universiteit Utrecht op gezag van de rector magnificus, prof. dr. W.H. Gispen, ingevolge het besluit van het college voor promoties in het openbaar te verdedigen op dinsdag 28 november 2006 des middags te 2.30 uur door Mari Cornelis Wapenaar geboren op 14 juli 1958 te -

Rabbit Anti-NAT9 Antibody-SL19029R
SunLong Biotech Co.,LTD Tel: 0086-571- 56623320 Fax:0086-571- 56623318 E-mail:[email protected] www.sunlongbiotech.com Rabbit Anti-NAT9 antibody SL19029R Product Name: NAT9 Chinese Name: 乙酰转移酶9抗体 EBSP; Embryo brain specific protein; Embryo brain-specific protein; N- Alias: acetyltransferase 9; Nacetyltransferase 9; Nat9; NAT9_HUMAN. Organism Species: Rabbit Clonality: Polyclonal React Species: Human,Mouse,Rat,Dog, ELISA=1:500-1000IHC-P=1:400-800IHC-F=1:400-800ICC=1:100-500IF=1:100- 500(Paraffin sections need antigen repair) Applications: not yet tested in other applications. optimal dilutions/concentrations should be determined by the end user. Molecular weight: 23kDa Cellular localization: The nucleuscytoplasmicThe cell membraneExtracellular matrix Form: Lyophilized or Liquid Concentration: 1mg/ml immunogen: KLH conjugated synthetic peptide derived from human NAT9:101-200/207 Lsotype: IgGwww.sunlongbiotech.com Purification: affinity purified by Protein A Storage Buffer: 0.01M TBS(pH7.4) with 1% BSA, 0.03% Proclin300 and 50% Glycerol. Store at -20 °C for one year. Avoid repeated freeze/thaw cycles. The lyophilized antibody is stable at room temperature for at least one month and for greater than a year Storage: when kept at -20°C. When reconstituted in sterile pH 7.4 0.01M PBS or diluent of antibody the antibody is stable for at least two weeks at 2-4 °C. PubMed: PubMed NAT-9 is a 207 amino acid protein belonging to the acetyltransferase family and the GNAT subfamily. Containing a N-acetyltransferase domain, NAT-9 may be associated with psoriasis and psoriatic arthritis, a type of inflammatory/autoimmune disease that Product Detail: affects skin, tendons and/or joints of the hands and feet. -

Genome and Transcriptome Analysis of the Mealybug Maconellicoccus Hirsutus: a Model For
bioRxiv preprint doi: https://doi.org/10.1101/2020.05.22.110437; this version posted May 22, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. 1 Genome and transcriptome analysis of the mealybug Maconellicoccus hirsutus: A model for 2 genomic Imprinting 3 Surbhi Kohli 1¶, Parul Gulati 1¶, Jayant Maini 1, Shamsudheen KV2, Rajesh Pandey2, Vinod 4 Scaria2, Sridhar Sivasubbu2, Ankita Narang1 * #, Vani Brahmachari1* 5 6 7 1 Dr.B.R.Ambedkar Center for Biomedical Research, University of Delhi, Delhi, India 8 2 CSIR-Institute of Genomics and Integrative Biology, Delhi, India 9 # Current Address: Departments of Medical Genetics, Psychiatry, and Physiology & 10 Pharmacology, University of Calgary, 254 HMRB, 3330 Hospital Dr NW Calgary, AB T2N 11 4N1, CANADA 12 13 14 * Corresponding authors. 15 16 Email: [email protected], [email protected] (AN) 17 18 Email:[email protected] (VB) 19 20 21 ¶ These authors contributed equally to this work 22 23 Key words: Genomic Imprinting, epigenetics, mealybug, genome annotation, expansion, 24 horizontal gene transfer, transcriptome 25 26 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.05.22.110437; this version posted May 22, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. -

Genomic Analysis of the HER2/TOP2A Amplicon in Breast
Laboratory Investigation (2008) 88, 491–503 & 2008 USCAP, Inc All rights reserved 0023-6837/08 $30.00 Genomic analysis of the HER2/TOP2A amplicon in breast cancer and breast cancer cell lines Edurne Arriola1,*, Caterina Marchio1,2, David SP Tan1, Suzanne C Drury3, Maryou B Lambros1, Rachael Natrajan1, Socorro Maria Rodriguez-Pinilla4, Alan Mackay1, Narinder Tamber1, Kerry Fenwick1, Chris Jones5, Mitch Dowsett3, Alan Ashworth1 and Jorge S Reis-Filho1 HER2 and TOP2A are targets for the therapeutic agents trastuzumab and anthracyclines and are frequently amplified in breast cancers. The aims of this study were to provide a detailed molecular genetic analysis of the 17q12–q21 amplicon in breast cancers harbouring HER2/TOP2A co-amplification and to investigate additional recurrent co-amplifications in HER2/ TOP2A-co-amplified cancers. In total, 15 breast cancers with HER2 amplification, 10 of which also harboured TOP2A amplification, as defined by chromogenic in situ hybridisation, and 6 breast cancer cell lines known to be amplified for HER2 were subjected to high-resolution microarray-based comparative genomic hybridisation analysis. This revealed that the genomes of 12 cases were characterised by at least one localised region of clustered, relatively narrow peaks of amplification, with each cluster confined to a single chromosome arm (ie ‘firestorm’ pattern) and 3 cases displayed many narrow segments of duplication and deletion affecting the vast majority of chromosomes (ie ‘sawtooth’ pattern). The smallest region of amplification (SRA) on 17q12 in the whole series extended from 34.73 to 35.48 Mb, and encompassed HER2 but not TOP2A.InHER2/TOP2A-co-amplified samples, the SRA extended from 34.73 to 36.54 Mb, spanning a region of B1.8 Mb. -

Synaptic Signal Transduction and Transcriptional Control
Synaptic signal transduction and transcriptional control Thesis by Holly C. Beale In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy California Institute of Technology Pasadena, California 2010 (Submitted Friday 21st May, 2010) ii c 2010 Holly C. Beale All Rights Reserved iii This thesis is dedicated to Gwen Murdock Pollard, to the many people whose friendship and support exceeded anything I could have anticipated, and to Julia Scheinmann. iv Acknowledgments First I would like to thank my advisor, Mary Kennedy, for the the insights she pro- vided over the past seven years and for the freedom she gave me. The breadth of her scientific interest is inspiring. I would also like to thank the other members of my thesis committee, Paul Patterson, Paul Sternberg and the chair, Henry Lester, for their time and feedback over the years. In particular, I thank Paul Patterson for his writing suggestions, which have transformed how I think about my writing, and Henry Lester for his advice and teaching example. As a body, members of the Kennedy lab have been exemplars of insight, collabora- tion and persistence. Holly Carlisle, Tinh Luong and Tami Ursem were invaluable in the completion of this thesis. Andrew Medina-Marino provided a critical opportunity and example of kindness. Dado Marcora has been terrific geek company, a walking encyclopedia of methods and an asker of fundamental questions. Leslie Schenker has been the silent engine of the lab and is a delight every day. It has been an honor to work with these lab members and others past and present, including Mee Choi, Cheryl Gause, Irene Knuesel, Pat Manzerra, Ward Walkup, and Lori Washburn. -

Analysis of Novel Steroidogenic Factor-1 Targets in the Human Adrenal Gland
Analysis of novel Steroidogenic Factor-1 targets in the human adrenal gland Bruno Ferraz de Souza UCL Institute of Child Health University College London Thesis submitted for the degree of Doctor of Philosophy (Ph.D.) 2011 Declaration I, Bruno Ferraz de Souza, confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. Signed ……………………………………………………. Date …………………. 2 Abstract Steroidogenic Factor-1 (SF-1, NR5A1 ) is a nuclear receptor transcription factor that plays a central role in adrenal and reproductive biology. In humans, SF-1 regulates adrenal development and disruption of SF-1 or its known targets is associated with impaired adrenal function. Therefore, the identification of novel SF-1 targets could reveal important new mechanisms in adrenal development and disease. This thesis describes three approaches to identifying SF-1 targets in NCI-H295R human adrenocortical cells. SF-1-dependent regulation of CITED2 and PBX1 was investigated since these factors regulate adrenal development in mice through pathways shared with Sf-1. Expression of CITED2 and PBX1 was confirmed in the developing human adrenal, and SF-1 was found to bind to and activate the CITED2 promoter and to cooperate with DAX1 to activate the PBX1 promoter. SF-1 binding was investigated using chromatin immunoprecipitation microarrays (ChIP-on-chip). These studies revealed that SF-1 binds to the extended promoter of 445 genes, including factors involved in angiogenesis. Angiopoietin 2 ( ANGPT2 ) emerged as a key novel SF-1 target, confirmed by transactivational studies, suggesting that regulation of angiogenesis might be an important additional action of SF-1 during adrenal development and tumorigenesis.