Superstars in Two-Sided Markets: Exclusives Or Not?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Drafts April
ACTION ADVENTURE FIRST PERSON SHOOTER THIRD PERSON SHOOTER Star Wars: Jedi Fallen Dragon Quest Wolfenstein: Ace Combat 7: SU 81 Sea of Solitude Metro: Exodus 83 Anthem 61 The Darwin Project Order Builders II Youngblood Ancestors; The Shenmue 3 Devil May Cry 5 88 The Dark Pictures Halo: Infinite Far Cry New Dawn 74 Control The Division 2 83 Human Kind Odyssey Earth Defense Force: Skull and Bones Nioh 2 Skull and Bones The Sinking City Rage 2 Doom Eternal Left Alive 37 Iron Rain Mechwarrior 5: Mechwarrior 5: Remnant Rise From Dying Light 2 The Blackout Club Deep Rock Galactic Generation Zero 49 Gears 5 Mercenaries Mercenaries The Ashes FIGHTING SPORTS RACING STRATEGY Jump Force 58 Mortal Kombat 11 NBA 2K ‘20 NBA Live ‘20 Sonic Team Racing Trials Rising 80 Age of Empires 4 Wargroove 83 Total War Dead or Alive 6 75 Dirt Rally 2.0 83 GTR 3 Conan Unconquered Samurai Shodown NHL ‘20 Madden ‘20 Three Kingdoms Granblue Fantasy Shovel Knight: MLB The Show 19 85 PES 2020 Dangerous Driving Xenon Racer 57 Tropico 6 78 Re-Legion 52 Versus Showdown Them’s Fighting Pro Fishing Monster Energy The Grand Tour KILL la KILL - IF FIFA ‘20 - 73 48 Imperator Rome Phoenix Point Herds Simulator Supercross 2 Game RPG ACTION RPG INDIE & ARCADE GAMES (PICK 2) Indivisible Digimon Survive God Eater 3 73 Kingdom Hearts 3 85 UFO50 Streets of Rage 4 Jenny LeClue Tunche Away: Journey To Town Greedfall Biomutant Code Vein 61 Hyper Jam 74 Toe Jame & Earl:BitG 72 Sayonara Wild Hearts The Unexpected Wasteland 3 Torchlight: Frontiers The Outer Worlds The Surge 2 Moving Out Untitled -

Family Friendly Magazine 142 in PDF Format
Family Friendly Gaming The VOICE of TM the FAMILY in GAMING The Lego Move 2 Videogame wants you to build it! Pokemon Sword, Pokemon Shield, Snooker 19, and more in this fabu- lous issue!! ISSUE #142 May 2019 CONTENTS ISSUE #142 May 2019 CONTENTS Links: Home Page Section Page(s) Editor’s Desk 4 Female Side 5 Comics 7 Sound Off 8 - 10 Look Back 12 Quiz 13 Devotional 14 Helpful Thoughts 15 In The News 16 - 23 We Would Play That! 24 Reviews 25 - 37 Sports 38 - 41 Developing Games 42 - 67 Now Playing 68 - 83 Last Minute Tidbits 84 - 106 “Family Friendly Gaming” is trademarked. Contents of Family Friendly Gaming is the copyright of Paul Bury, and Yolanda Bury with the exception of trademarks and related indicia (example Digital Praise); which are prop- erty of their individual owners. Use of anything in Family Friendly Gaming that Paul and Yolanda Bury claims copyright to is a violation of federal copyright law. Contact the editor at the business address of: Family Friendly Gaming 7910 Autumn Creek Drive Cordova, TN 38018 [email protected] Trademark Notice Nintendo, Sony, Microsoft all have trademarks on their respective machines, and games. The current seal of approval, and boy/girl pics were drawn by Elijah Hughes thanks to a wonderful donation from Tim Emmerich. Peter and Noah are inspiration to their parents. Family Friendly Gaming Page 2 Page 3 Family Friendly Gaming Editor’s Desk FEMALE SIDE are new to us. We are adapting and chang- diction is a serious problem. Yes there needs On the Cusp ing as we have been required to. -
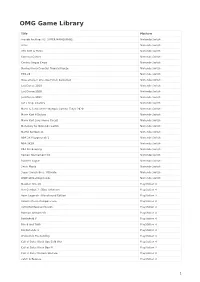
OMG Game Library
OMG Game Library Title Platform Arcade Archives VS. SUPER MARIO BROS. Nintendo Switch Arms Nintendo Switch ATV Drift & Tricks Nintendo Switch Carnival Games Nintendo Switch Contra: Rogue Corps Nintendo Switch Donkey Kong Country: Tropical Freeze Nintendo Switch FIFA 20 Nintendo Switch Guacamelee! One-Two Punch Collection Nintendo Switch Just Dance 2019 Nintendo Switch Just Dance 2020 Nintendo Switch Just Dance 2021 Nintendo Switch Let’s Sing: Country Nintendo Switch Mario & Sonic at the Olympic Games: Tokyo 2020 Nintendo Switch Mario Kart 8 Deluxe Nintendo Switch Mario Kart Live: Home Circuit Nintendo Switch Monopoly for Nintendo Switch Nintendo Switch Mortal Kombat 11 Nintendo Switch NBA 2K Playgrounds 2 Nintendo Switch NBA 2K20 Nintendo Switch PBA Pro Bowling Nintendo Switch Pokkén Tournament DX Nintendo Switch Rocket League Nintendo Switch Sonic Mania Nintendo Switch Super Smash Bros. Ultimate Nintendo Switch WWE 2K Battlegrounds Nintendo Switch Madden NFL 20 PlayStation 4 Ace Combat 7: Skies Unknown PlayStation 4 Apex Legends - Bloodhound Edition PlayStation 4 Assetto Corsa Competizione PlayStation 4 Astro Bot Rescue Mission PlayStation 4 Batman Arkham VR PlayStation 4 Battlefield V PlayStation 4 Blood and Truth PlayStation 4 Borderlands 3 PlayStation 4 Brunswick Pro Bowling PlayStation 4 Call of Duty: Black Ops Cold War PlayStation 4 Call of Duty: Black Ops III PlayStation 4 Call of Duty: Modern Warfare PlayStation 4 catch & Release PlayStation 4 1 OMG Game Library country lets sing PlayStation 4 Creed: Rise to Glory PlayStation 4 -
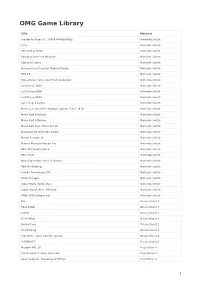
OMG Game Library
OMG Game Library Title Platform Arcade Archives VS. SUPER MARIO BROS. Nintendo Switch Arms Nintendo Switch ATV Drift & Tricks Nintendo Switch Bendy and the Ink Machine Nintendo Switch Carnival Games Nintendo Switch Donkey Kong Country: Tropical Freeze Nintendo Switch FIFA 20 Nintendo Switch Guacamelee! One-Two Punch Collection Nintendo Switch Just Dance 2019 Nintendo Switch Just Dance 2020 Nintendo Switch Just Dance 2021 Nintendo Switch Let’s Sing: Country Nintendo Switch Mario & Sonic at the Olympic Games: Tokyo 2020 Nintendo Switch Mario Kart 8 Deluxe Nintendo Switch Mario Kart 8 Deluxe Nintendo Switch Mario Kart Live: Home Circuit Nintendo Switch Monopoly for Nintendo Switch Nintendo Switch Mortal Kombat 11 Nintendo Switch Namco Museum Arcade Pac Nintendo Switch NBA 2K Playgrounds 2 Nintendo Switch NBA 2K20 Nintendo Switch New Super Mario Bros. U Deluxe Nintendo Switch PBA Pro Bowling Nintendo Switch Pokkén Tournament DX Nintendo Switch Rocket League Nintendo Switch Super Mario 3D All-Stars Nintendo Switch Super Smash Bros. Ultimate Nintendo Switch WWE 2K Battlegrounds Nintendo Switch Bait Oculus Quest 2 Beat Saber Oculus Quest 2 Creed Oculus Quest 2 Pistol Whip Oculus Quest 2 Racket Fury Oculus Quest 2 Real Fishing Oculus Quest 2 Stat Wars : Tales from the galaxy Oculus Quest 2 SUPERHOT Oculus Quest 2 Madden NFL 20 PlayStation 4 Ace Combat 7: Skies Unknown PlayStation 4 Apex Legends - Bloodhound Edition PlayStation 4 1 OMG Game Library Assetto Corsa Competizione PlayStation 4 Astro Bot Rescue Mission PlayStation 4 Batman Arkham VR -

FTC Inside the Game: Unlocking the Consumer Issues Surrounding Loot Boxes Workshop Transcript Segment 1
Inside the Game: Unlocking the Consumer Issues Surrounding Loot Boxes – An FTC Workshop August 7, 2019 Segment 1 Transcript MARY JOHNSON: Good morning, everyone. My name is Mary Johnson. I'm an attorney in the division of Advertising Practices in FTC's Bureau of Consumer Protection. Thank you for your interest in today's topic, "Consumer Issues Related to Video Game Loot Boxes and Microtransactions." Before we get started with the program, I need to review some administrative details. I don't have a catchy video to hold your attention, so please listen carefully. Please silence any mobile phones and other electronic devices. If you must use them during the workshop, please be respectful of the speakers and your fellow audience members. Please be aware that if you leave the Constitution Center building for any reason during the workshop, you will have to go back through security screening again when you return. So bear this in mind and plan ahead, especially if you are participating on a panel, so we can do our best to remain on schedule. If you received a lanyard with a plastic FTC event security badge, please return your badge to security when you leave for the day. We do reuse those for multiple events. So now some important emergency procedures. If an emergency occurs that requires evacuation of the building, an alarm will sound. Everyone should leave the building in an orderly manner through the main 7th Street exit. After leaving the building, turn left and proceed down 7th Street to E Street to the FTC emergency assembly area. -

Lemasters-Mastersreport
The Report Committee for William Norman LeMasters Certifies that this is the approved version of the following report: Representation in Action: An Overview of the Avatar/Attribute Relationship in Sports-Themed Video Games APPROVED BY SUPERVISING COMMITTEE: Kathryn Fuller-Seeley, Supervisor Alisa Perren Representation in Action: An Overview of the Avatar/Attribute Relationship in Sports-Themed Video Games by William Norman LeMasters Report Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Master of Arts The University of Texas at Austin August 2020 Abstract Representation in Action: An Overview of the Avatar/Attribute Relationship in Sports-Themed Video Games by William Norman LeMasters, M.A. The University of Texas at Austin, 2020 Supervisor: Kathryn Fuller-Seeley Representation in video games has thus far centered primarily on the aesthetics of a digital avatar. Using sports-themed video games, we can broaden the understanding of representation to include action or the ways athletes perform within any given game by analyzing attribute allocation, the primary method of avatar differentiation within the sports genre, and how digital bodies play a role in shaping an athlete’s real-world identity. Sports-themed video games are immensely popular with the big 3 franchises, Madden, FIFA and the NBA 2K series, routinely finishing among the best-selling video game titles year in and year out. Due to their popularity, scholars have turned some attention toward this genre of games although almost all articles pertain solely to the aesthetic representations of athlete avatars while comparatively few attempts have been made to breakdown the relationship between an athlete’s real statistics and how these statistics figure into the representation of their digitized body. -

How to Download Mlb the Show 15 Roster Update
How to download mlb the show 15 roster update LINK TO DOWNLOAD rows · The Show Nation is where you talk about MLB The Show! Please Wait. News; Games; . For MLB The Show on the PlayStation 4, a GameFAQs message board topic titled "How to undate MLB 15 to current rosters". 13/4/ · The first in-season roster update for MLB The Show arrived today. It represents the first opportunity for SCEA to add players to the game who made their Major League debuts over the course of the season’s opening week. 22/7/ · MLB The Show Last Gen Rosters. All roster talk for the PS3 and Vita versions of MLB: The Show Below you will find a list of discussions in the MLB The Show Last Gen Rosters forums at the Operation Sports Forums. For the most realistic baseball experience, MLB The Show 18, gives players the feature to save the most recent roster update to their game, and doing so is quite easy. If you don't know how to. rows · Roster Update Select Roster Update September 27, September 20, . 38 rows · MLB 18 The Show. Shop Buy Stubs; Buy Packs; Ticket Counter; Community Market Roster . MLB 18 The Show. Shop Buy Stubs; Buy Packs; Ticket Counter; Community Market Roster Updates Leaderboards Home Run Derby; Challenge of the Week; Dynasty Seasons; Battle Royale; Community; Hello Guest PSN Login Roster Update Attribute Changes +15 ARM STR. 63 +15 ARM ACC. 51 +5 RCT. 54 +10 SPD. 54 +16 Ben Zobrist #18 2B: Cubs: 74 Anytime there's a roster update, it should give you the option to download it when you first start up the game (if your roster isn't up to date). -

Drafts URNK April
CHRISTIAN ALEX GENRE ACTIVE ROSTER SCORE BENCH GENRE ACTIVE ROSTER SCORE BENCH Action Ace Combat 7 81 Star Wars: JFO Action Devil May Cry 5 88 - Adventure Ancestors - The Blackout Club Adventure DQ Builders 2 - Sea of Solitude FPS Metro: Exodus 83 - FPS Far Cry New Dawn 74 Atomic Heart TPS Control - - TPS Anthem 62 - Fighting Granblue F Versus - KILL la KILL - IF Fighting Jump Force 58 - Sports FIFA ‘20 - - Sports MLB The Show ‘19 85 - Racing Trials Rising 80 - Racing Dirt Rally 2.0 83 - Strategy Phoenix Point - - Strategy Wargroove 83 Imperator Rome RPG Town - Torchlight RPG Star Renegade - - Action RPG Rebel Outlaw Galaxy - The Outer Worlds Action RPG Code Vein - - Indie & Arcade UFO 50 - Children Morta Indie & Arcade Sayonara Wild Hearts - Goose Game Indie & Arcade Harold Halibut - - Indie & Arcade Toe Jam and Earl: BITG 72 Super Animal Royal Platformer Spelunky 2 - - Platformer Yoshi’s Crafted World 80 Psychonauts 2 Nintendo Switch Luigi’s Mansion 3 - - Nintendo Switch Animal Crossing - - Playstation 4 Dreams - TLOU 2 Playstation 4 Babylon’s Fall - - Xbox One Ooblets - Session Xbox One Crackdown 63 Sable - Battletoads CURRENT TOTAL SCORE: 244 CURRENT TOTAL SCORE: 749 DAN TOM GENRE ACTIVE ROSTER SCORE BENCH GENRE ACTIVE ROSTER SCORE BENCH Action Shenmue 3 - Dying Light 2 Action Nioh 2 - - Adventure The Sinking City - - Adventure Judgement - - FPS Rage 2 - - FPS Doom Eternal - Wolfenstein TPS Left Alive 37 Gears of War 5 TPS Division 2 83 - Fighting Dead or Alive 6 75 - Fighting Mortal Kombat 11 - - Sports Madden ‘20 - NHL ‘20 Sports -
Inside the Game: Unlocking the Consumer Issues
1 2 3 4 5 6 INSIDE THE GAME: UNLOCKING THE CONSUMER ISSUES 7 SURROUNDING LOOT BOXES 8 AUGUST 7, 2019 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2 Workshop Inside the Game: Unlocking the Consumer Issues Surrounding Loot Boxes 8/7/2019 1 C O N T E N T S 2 PAGE 3 Welcome and Opening Remarks 7 4 5 Panel 1: Treasure or Trifle? A Macro Look 6 at Microtransactions 13 7 8 Panel 2: Head in the Game - What Drives Loot 9 Box Spending? 112 10 11 Panel 3: A Level Playing Field - What’s Fair 12 Game 167 13 14 Closing Remarks 232 15 16 17 18 19 20 21 22 23 24 25 For The Record, Inc. (301) 870-8025 - www.ftrinc.net - (800) 921-5555 3 Workshop Inside the Game: Unlocking the Consumer Issues Surrounding Loot Boxes 8/7/2019 1 P R O C E E D I N G S 2 INSIDE THE GAME: UNLOCKING THE CONSUMER ISSUES 3 SURROUNDING LOOT BOXES 4 MS. JOHNSON: Good morning, everyone. My 5 name is Mary Johnson. I’m an attorney in the Division 6 of Advertising Practices in FTC’s Bureau of Consumer 7 Protection. Thank you for your interest in today’s 8 topic, “Consumer Issues Related to Video Game Loot 9 Boxes and Microtransactions.” 10 Before we get started with the program, I 11 need to review some administrative details. I don’t 12 have a catchy video to hold your attention, so please 13 listen carefully. -
An Investigation of Monetization Strategies in Aaa Video Games
Master Thesis MSc in Management of Innovation and Business Development AN INVESTIGATION OF MONETIZATION STRATEGIES IN AAA VIDEO GAMES By Mariusz Patryk Diaczok & Patrick Tronier Supervisor: Just Pedersen Date of submission: 14th of May 2019 Character count / number of pages: 270.395 / 119 Abstract The AAA video game industry has recently been associated with multiple controversies and community outrages, most commonly attributed to aggressive monetization strategies. Due to the rapid evolution of the industry in question, the body of academic literature is quite lacking, especially with regard to developments that are more recent. The authors gathered research investigating the impact of a number of factors, related to the most prevalent monetization strategies, on the games themselves, and combine these insights, in order to create a foundation for a holistic theory of these relationships. A qualitative study, in the form of a literature review, was undertaken to explore the various factors impacted by the chosen monetization strategy. In addition, a quantitative study was conducted to investigate how the choice of monetization strategy affects the rating scores given by critics and consumers. These studies add to the understanding of how a chosen strategy can affect the consumer perception of the game, which is directly related to the generated revenue. Furthermore, the literature review provides a rough outline for the interaction between consumer purchase motivations, purchase incentives implemented into the games and their effectiveness. -

OMG Game Library
OMG Game Library Title Platform Arcade Archives VS. SUPER MARIO BROS. Nintendo Switch Arms Nintendo Switch ATV Drift & Tricks Nintendo Switch Carnival Games Nintendo Switch Contra: Rogue Corps Nintendo Switch Donkey Kong Country: Tropical Freeze Nintendo Switch FIFA 20 Nintendo Switch Guacamelee! One-Two Punch Collection Nintendo Switch Just Dance 2019 Nintendo Switch Just Dance 2020 Nintendo Switch Let’s Sing: Country Nintendo Switch Mario & Sonic at the Olympic Games: Tokyo 2020 Nintendo Switch Mario + Rabbids Kingdom Battle Nintendo Switch Mario Kart 8 Deluxe Nintendo Switch Mortal Kombat 11 Nintendo Switch NBA 2K Playgrounds 2 Nintendo Switch NBA 2K20 Nintendo Switch Pokkén Tournament DX Nintendo Switch Sonic Mania Nintendo Switch Star Wars Pinball Nintendo Switch Super Mario Odyssey Nintendo Switch Super Smash Bros. Ultimate Nintendo Switch WWE 2K Battlegrounds Nintendo Switch Madden NFL 20 PlayStation 4 Ace Combat 7: Skies Unknown PlayStation 4 Angry Birds: Star Wars PlayStation 4 Apex Legends - Bloodhound Edition PlayStation 4 Astro Bot Rescue Mission PlayStation 4 Batman Arkham VR PlayStation 4 Battlefield V PlayStation 4 Borderlands 3 PlayStation 4 Brunswick Pro Bowling PlayStation 4 Call of Duty: Black Ops III PlayStation 4 Call of Duty: Modern Warfare PlayStation 4 catch & Release PlayStation 4 country lets sing PlayStation 4 Creed: Rise to Glory PlayStation 4 dick wilde 2 PlayStation 4 DOOM VFR PlayStation 4 1 OMG Game Library EA Sports UFC 3 PlayStation 4 Fortnite PlayStation 4 Ghost Giant PlayStation 4 Gran Turismo Sport -

2019 Hip2save Black Friday Price Comparison Spreadsheet
Hip2Save's BLACK FRIDAY Comparison Cheat Sheet – HOTTEST Buys at the CHEAPEST Prices! Item/Product Price Store Notes Electronics DVD PLAYERS BLU-RAY PLAYERS LG Streaming Audio Blu-Ray Player $49.99 Best Buy Best Buy Exclusive; Doors Open Thurs 11/28 at 5pm; Shop Online All Day LG Streaming Audio Wi-Fi Built-In Blu-Ray Player $49.99 Best Buy Doors Open Thurs 11/28 at 5pm; Shop Online All Day LG UBK80 4K Ultra HD Blu-Ray Player $99.99 Best Buy Doors Open Thurs 11/28 at 5pm; Shop Online All Day Samsung Streaming 4K Ultra HD Audio Wi-Fi Built-In Blu-Ray Player $149.99 Best Buy Doors Open Thurs 11/28 at 5pm; Shop Online All Day Sony 4K Ultra HD Blu-Ray Player $129.99 Target Doors Open 5pm Thurs, Close 1am Fri, Re-Open 7am Fri; Friday 11/29 ONLY Spend $50 in a single transaction In-Store or Online and Receive a Coupon for 20% Off a Future Shopping Trip Between 12/3-12/14; Friday 11/29 ONLY Spend $50 in a single transaction In-Store or Online and Receive a Coupon for 20% Off a Future Shopping Trip Between 12/3-12/14 Sony Streakming 4K Ultra HD Hi-Res Audio Wi-Fi Built-In Blu-Ray Player $129.99 Best Buy Doors Open Thurs 11/28 at 5pm; Shop Online All Day Sony UBP-X800M2 Streaming 4K Ultra HD Hi-Res Audio Wi-Fi Built-In Blu-Ray Player $199.99 Best Buy Doors Open Thurs 11/28 at 5pm; Shop Online All Day APPLE PRODUCTS Apple AirPods Pro $249.99 Target Doors Open 5pm Thurs, Close 1am Fri, Re-Open 7am Fri; Friday 11/29 ONLY Spend $50 in a single transaction In-Store or Online and Receive a Coupon for 20% Off a Future Shopping Trip Between 12/3-12/14