Distinguishing Between Stellar and Planetary Companions with Phase Monitoring
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Phases of Venus and Galileo
Galileo and the phases of Venus I) Periods of Venus 1) Synodical period and phases The synodic period1 of Venus is 584 days The superior2 conjunction occured on 11 may 1610. Calculate the date of the quadrature, of the inferior conjunction and of the next superior conjunction, supposing the motions of the Earth and Venus are circular and uniform. In fact the next superior conjunction occured on 11 december 1611 and inferior conjunction on 26 february 1611. 2) Sidereal period The sidereal period of the Earth is 365.25 days. Calculate the sidereal period of Venus. II) Phases on Venus in geo and heliocentric models 1) Phases in differents models 1) Determine the phases of Venus in geocentric models, where the Earth is at the center of the universe and planets orbit around (Venus “above” or “below” the sun) * Pseudo-Aristoteles model : Earth (center)-Moon-Sun-Mercury-Venus-Mars-Jupiter-Saturne * Ptolemeo’s model : Earth (center)-Moon-Mercury-Venus-Sun-Mars-Jupiter-Saturne 2) Determine the phases of Venus in the heliocentric model, where planets orbit around the sun. Copernican system : Sun (center)-Mercury-Venus-Earth-Mars-Jupiter-Saturne 2) Observations of Galileo Galileo (1564-1642) observed Venus in 1610-1611 with a telescope. Read the letters of Galileo. May we conclude that the Copernican model is the only one available ? When did Galileo begins to observe Venus? Give the approximate dates of the quadrature and of the inferior conjunction? What are the approximate dates of the 5 observations of Galileo supposing the figure from the Essayer, was drawn in 1610-1611 1 The synodic period is the time that it takes for the object to reappear at the same point in the sky, relative to the Sun, as observed from Earth; i.e. -

Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation
Lurking in the Shadows: Wide-Separation Gas Giants as Tracers of Planet Formation Thesis by Marta Levesque Bryan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2018 Defended May 1, 2018 ii © 2018 Marta Levesque Bryan ORCID: [0000-0002-6076-5967] All rights reserved iii ACKNOWLEDGEMENTS First and foremost I would like to thank Heather Knutson, who I had the great privilege of working with as my thesis advisor. Her encouragement, guidance, and perspective helped me navigate many a challenging problem, and my conversations with her were a consistent source of positivity and learning throughout my time at Caltech. I leave graduate school a better scientist and person for having her as a role model. Heather fostered a wonderfully positive and supportive environment for her students, giving us the space to explore and grow - I could not have asked for a better advisor or research experience. I would also like to thank Konstantin Batygin for enthusiastic and illuminating discussions that always left me more excited to explore the result at hand. Thank you as well to Dimitri Mawet for providing both expertise and contagious optimism for some of my latest direct imaging endeavors. Thank you to the rest of my thesis committee, namely Geoff Blake, Evan Kirby, and Chuck Steidel for their support, helpful conversations, and insightful questions. I am grateful to have had the opportunity to collaborate with Brendan Bowler. His talk at Caltech my second year of graduate school introduced me to an unexpected population of massive wide-separation planetary-mass companions, and lead to a long-running collaboration from which several of my thesis projects were born. -

Planetary Phase Variations of the 55 Cancri System
The Astrophysical Journal, 740:61 (7pp), 2011 October 20 doi:10.1088/0004-637X/740/2/61 C 2011. The American Astronomical Society. All rights reserved. Printed in the U.S.A. PLANETARY PHASE VARIATIONS OF THE 55 CANCRI SYSTEM Stephen R. Kane1, Dawn M. Gelino1, David R. Ciardi1, Diana Dragomir1,2, and Kaspar von Braun1 1 NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue, Pasadena, CA 91125, USA; [email protected] 2 Department of Physics & Astronomy, University of British Columbia, Vancouver, BC V6T1Z1, Canada Received 2011 May 6; accepted 2011 July 21; published 2011 September 29 ABSTRACT Characterization of the composition, surface properties, and atmospheric conditions of exoplanets is a rapidly progressing field as the data to study such aspects become more accessible. Bright targets, such as the multi-planet 55 Cancri system, allow an opportunity to achieve high signal-to-noise for the detection of photometric phase variations to constrain the planetary albedos. The recent discovery that innermost planet, 55 Cancri e, transits the host star introduces new prospects for studying this system. Here we calculate photometric phase curves at optical wavelengths for the system with varying assumptions for the surface and atmospheric properties of 55 Cancri e. We show that the large differences in geometric albedo allows one to distinguish between various surface models, that the scattering phase function cannot be constrained with foreseeable data, and that planet b will contribute significantly to the phase variation, depending upon the surface of planet e. We discuss detection limits and how these models may be used with future instrumentation to further characterize these planets and distinguish between various assumptions regarding surface conditions. -

On the Use of Planetary Science Data for Studying Extrasolar Planets a Science Frontier White Paper Submitted to the Astronomy & Astrophysics 2020 Decadal Survey
On the Use of Planetary Science Data for Studying Extrasolar Planets A science frontier white paper submitted to the Astronomy & Astrophysics 2020 Decadal Survey Thematic Area: Planetary Systems Principal Author Daniel J. Crichton Jet Propulsion Laboratory, California Institute of Technology [email protected] 818-354-9155 Co-Authors: J. Steve Hughes, Gael Roudier, Robert West, Jeffrey Jewell, Geoffrey Bryden, Mark Swain, T. Joseph W. Lazio (Jet Propulsion Laboratory, California Institute of Technology) There is an opportunity to advance both solar system and extrasolar planetary studies that does not require the construction of new telescopes or new missions but better use and access to inter-disciplinary data sets. This approach leverages significant investment from NASA and international space agencies in exploring this solar system and using those discoveries as “ground truth” for the study of extrasolar planets. This white paper illustrates the potential, using phase curves and atmospheric modeling as specific examples. A key advance required to realize this potential is to enable seamless discovery and access within and between planetary science and astronomical data sets. Further, seamless data discovery and access also expands the availability of science, allowing researchers and students at a variety of institutions, equipped only with Internet access and a decent computer to conduct cutting-edge research. © 2019 California Institute of Technology. Government sponsorship acknowledged. Pre-decisional - For planning -
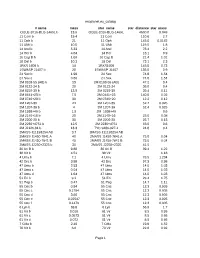
Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55 -

A Search for Variability and Transit Signatures In
A SEARCH FOR VARIABILITY AND TRANSIT SIGNATURES IN HIPPARCOS PHOTOMETRIC DATA A thesis presented to the faculty of 3 ^ San Francisco State University Zo\% In partial fulfilment of W* The Requirements for The Degree Master of Science In Physics: Astronomy by Badrinath Thirumalachari San JVancisco, California December 2018 Copyright by Badrinath Thirumalachari 2018 CERTIFICATION OF APPROVAL I certify that I have read A SEARCH FOR VARIABILITY AND TRANSIT SIGNATURES IN HIPPARCOS PHOTOMETRIC DATA by Badrinath Thirumalachari and that in my opinion this work meets the criteria for approving a thesis submitted in partial fulfillment of the requirements for the degree: Master of Science in Physics: Astronomy at San Francisco State University. fov- Dr. Stephen Kane, Ph.D. Astrophysics Associate Professor of Planetary Astrophysics Dr. Uo&eph Barranco, Ph.D. .%trtJphysics Chairfe Associate Professor of Physics K + A Q , L a . Dr. Ron Marzke, Ph.D. Astronomy Assoc. Dean of College of Science & Engineering A SEARCH FOR VARIABILITY AND TRANSIT SIGNATURES IN HIPPARCOS PHOTOMETRIC DATA Badrinath Thirumalachari San Francisco State University 2018 The study and characterization of exoplanets has picked up pace rapidly over the past few decades with the invention of newer techniques and instruments. Detecting transits in stellar photometric data around stars already known to harbor exoplanets is crucial for exoplanet characterization. Due to these advancements we now have oceans of data and coming up with an automated way of performing exoplanet characterization is a challenge. In this thesis I describe one such method to search for transits in Hipparcos dataset containing photometric data for over 118000 stars. The radial velocity method has discovered a lot of planets around bright host stars and a follow up transit detection will give us the density of the exoplanet. -

ON the INCLINATION DEPENDENCE of EXOPLANET PHASE SIGNATURES Stephen R
The Astrophysical Journal, 729:74 (6pp), 2011 March 1 doi:10.1088/0004-637X/729/1/74 C 2011. The American Astronomical Society. All rights reserved. Printed in the U.S.A. ON THE INCLINATION DEPENDENCE OF EXOPLANET PHASE SIGNATURES Stephen R. Kane and Dawn M. Gelino NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue, Pasadena, CA 91125, USA; [email protected] Received 2011 December 2; accepted 2011 January 5; published 2011 February 10 ABSTRACT Improved photometric sensitivity from space-based telescopes has enabled the detection of phase variations for a small sample of hot Jupiters. However, exoplanets in highly eccentric orbits present unique opportunities to study the effects of drastically changing incident flux on the upper atmospheres of giant planets. Here we expand upon previous studies of phase functions for these planets at optical wavelengths by investigating the effects of orbital inclination on the flux ratio as it interacts with the other effects induced by orbital eccentricity. We determine optimal orbital inclinations for maximum flux ratios and combine these calculations with those of projected separation for application to coronagraphic observations. These are applied to several of the known exoplanets which may serve as potential targets in current and future coronagraph experiments. Key words: planetary systems – techniques: photometric 1. INTRODUCTION and inclination for a given eccentricity. We further calculate projected separations at apastron as a function of inclination The changing phases of an exoplanet as it orbits the host star and determine their correspondence with maximum flux ratio have long been considered as a means for their detection and locations. -

Mètodes De Detecció I Anàlisi D'exoplanetes
MÈTODES DE DETECCIÓ I ANÀLISI D’EXOPLANETES Rubén Soussé Villa 2n de Batxillerat Tutora: Dolors Romero IES XXV Olimpíada 13/1/2011 Mètodes de detecció i anàlisi d’exoplanetes . Índex - Introducció ............................................................................................. 5 [ Marc Teòric ] 1. L’Univers ............................................................................................... 6 1.1 Les estrelles .................................................................................. 6 1.1.1 Vida de les estrelles .............................................................. 7 1.1.2 Classes espectrals .................................................................9 1.1.3 Magnitud ........................................................................... 9 1.2 Sistemes planetaris: El Sistema Solar .............................................. 10 1.2.1 Formació ......................................................................... 11 1.2.2 Planetes .......................................................................... 13 2. Planetes extrasolars ............................................................................ 19 2.1 Denominació .............................................................................. 19 2.2 Història dels exoplanetes .............................................................. 20 2.3 Mètodes per detectar-los i saber-ne les característiques ..................... 26 2.3.1 Oscil·lació Doppler ........................................................... 27 2.3.2 Trànsits -

Search for Brown-Dwarf Companions of Stars⋆⋆⋆
A&A 525, A95 (2011) Astronomy DOI: 10.1051/0004-6361/201015427 & c ESO 2010 Astrophysics Search for brown-dwarf companions of stars, J. Sahlmann1,2, D. Ségransan1,D.Queloz1,S.Udry1,N.C.Santos3,4, M. Marmier1,M.Mayor1, D. Naef1,F.Pepe1, and S. Zucker5 1 Observatoire de Genève, Université de Genève, 51 Chemin des Maillettes, 1290 Sauverny, Switzerland e-mail: [email protected] 2 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany 3 Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal 4 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Portugal 5 Department of Geophysics and Planetary Sciences, Tel Aviv University, Tel Aviv 69978, Israel Received 19 July 2010 / Accepted 23 September 2010 ABSTRACT Context. The frequency of brown-dwarf companions in close orbit around Sun-like stars is low compared to the frequency of plane- tary and stellar companions. There is presently no comprehensive explanation of this lack of brown-dwarf companions. Aims. By combining the orbital solutions obtained from stellar radial-velocity curves and Hipparcos astrometric measurements, we attempt to determine the orbit inclinations and therefore the masses of the orbiting companions. By determining the masses of poten- tial brown-dwarf companions, we improve our knowledge of the companion mass-function. Methods. The radial-velocity solutions revealing potential brown-dwarf companions are obtained for stars from the CORALIE and HARPS planet-search surveys or from the literature. The best Keplerian fit to our radial-velocity measurements is found using the Levenberg-Marquardt method. -

1 Revisiting 154-Day Periodicity in the Occurrence of Hard Flares. A
Revisiting 154-day periodicity in the occurrence of hard flares. A planetary influence? Ian Edmonds 12 Lentara St, Kenmore, Brisbane, Australia 4069. Ph/Fax 61 7 3378 6586, [email protected] Keywords: flare periodicity; planetary model; sunspot emergence; Mercury-Earth conjunction. Abstract. Rieger et al (1984) reported observations of a 154 day periodicity in flares during solar cycle 21. This paper discusses the observations in the light of a simple empirical planetary model of sunspot emergence. The planetary model predicts sunspot emergence when Mercury and Earth approach conjunction and Mercury approaches the Sun. We show that the reported times of flare activity are coherent with the planetary model. While the base period of the model is 170 days, the average model period, over the interval of flare recordings, is 157 days due to a 180 degree phase change in the planetary forcing near the middle of the record interval. We conclude that the periodicity at 154 days arises when the phase change in planetary forcing and the resulting progressive phase change in total sunspot area emergence and flare occurrence shifts the major peak in the flare spectrum from the planetary forcing period, 170 days, to 154 days. 1. Introduction. The observation of an ~ 154 day periodicity in the occurrence of hard flares, Rieger et al (1984), hereafter R84, initiated a now 32 year long investigation of mid-range, 40 – 2000 day, periodicities in solar activity. R84 analysed 139 flares recorded by the gamma ray spectrometer on the Solar Maximum Mission (solar cycle 21) from February 1980 through to the end of 1983 when recording ceased. -

Comprehensive Wide-Band Magnitudes and Albedos for the Planets, with Applications to Exo-Planets and Planet Nine
Comprehensive Wide-Band Magnitudes and Albedos for the Planets, With Applications to Exo-Planets and Planet Nine Anthony Mallama 14012 Lancaster Lane, Bowie, MD, 20715, USA [email protected] Bruce Krobusek 5950 King Hill Drive, Farmington, NY, 14425, USA [email protected] Hristo Pavlov 9 Chad Place, St. Clair, NSW 2759, Australia [email protected] Prepared for Icarus Pages: 49 Figures: 1 Tables: 37 Original version submitted: 2016 April 22 Reviewer comments received: 2016 July 26 Revised manuscript submitted: 2016 August 30 Accepted for publication by Icarus: 2016 September 14 Abstract Complete sets of reference magnitudes in all 7 Johnson-Cousins bands (U, B, V, R, I, RC and IC) and the 5 principal Sloan bands (u’, g’, r’, i', and z’) are presented for the 8 planets. These data are accompanied by illumination phase functions and other formulas which characterize the instantaneous brightness of the planets. The main source of Johnson-Cousins magnitudes is a series of individualized photometric studies reported in recent years. Gaps in that dataset were filled with magnitudes synthesized in this study from published spectrophotometry. The planetary Sloan magnitudes, which are established here for the first time, are an average of newly recorded Sloan filter photometry, synthetic magnitudes and values transformed from the Johnson-Cousins system. Geometric albedos derived from these two sets of magnitudes are consistent within each photometric system and between the systems for all planets and in all bands. This consistency validates the albedos themselves as well as the magnitudes from which they were derived. In addition, a quantity termed the delta stellar magnitude is introduced to indicate the difference between the magnitude of a planet and that of its parent star. -

Tidal Deformation of Planets and Satellites: Models and Methods for Laser- and Radar Altimetry
Tidal Deformation of Planets and Satellites: Models and Methods for Laser- and Radar Altimetry vorgelegt von Diplom Physiker Gregor Steinbr¨ugge geb. in Berlin von der Fakult¨atVI { Planen Bauen Umwelt der Technischen Universit¨atBerlin zur Erlangung des akademischen Grades Doktor der Naturwissenschaften - Dr. rer. nat. - genehmigte Dissertation Vorsitzender: Prof. Dr. Dr. h.c. Harald Schuh Gutachter: Prof. Dr. J¨urgenOberst Gutachter: Prof. Dr. Nicolas Thomas Gutachter: Prof. Dr. Tilman Spohn Tag der wissenschaftlichen Aussprache: 27.03.2018 Berlin 2018 2 Contents Title Page 1 Contents 3 List of Figures 7 List of Tables 9 1 Introduction 15 1.1 Structure of the Dissertation . 16 1.1.1 Icy Satellites . 17 1.1.2 Mercury . 20 1.2 Theory of Tides . 21 1.2.1 Tidal Potentials . 21 1.2.2 Response of Planetary Bodies to Tidal Forces . 23 1.3 Measuring Tidal Deformations . 25 1.3.1 Measurement Concepts . 25 1.3.2 Laser Altimetry . 25 1.3.3 Radar Altimetry . 26 1.4 Missions and Instruments . 27 1.4.1 REASON and the Europa Clipper Mission . 27 1.4.2 GALA and the JUICE Mission . 28 1.4.3 BELA and the BepiColombo Mission . 29 2 Research Paper I 31 2.1 Introduction . 32 2.2 Instrument Performance Modeling . 32 2.2.1 Link Budget . 32 2.2.2 Signal-to-Noise Ratio . 33 2.3 Expected Science Performance . 37 2.3.1 Topographic Coverage . 37 2.3.2 Slope and Roughness . 37 2.4 Tidal Deformation . 40 2.4.1 Covariance Analysis . 40 2.4.2 Numerical Simulation .