DOCSLIB.ORG

Resurrecting the Capital Asset Pricing Model

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Resurrecting the Capital Asset Pricing Model Resurrecting the Capital Asset Pricing Model Hammad Siddiqi University of Queensland [email protected] This Version: October 2016 Abstract The capital asset pricing model is generally considered incapable of explaining the stock market behavior. I show that this conclusion is premature, and incorporating a pragmatic approach to approximating optimal Bayesian inference in the model resurrects CAPM. The adjusted CAPM internalizes the well-known size, value, and momentum effects, high-alpha-of-low-beta-stocks, accruals, low volatility anomaly, stock-split anomaly, and reverse stock-split anomaly. The market equity premium is also larger with anchoring. Immediate applications of the adjusted CAPM include improved cost of equity calculation, and improved evaluation of managed portfolio performance. Keywords: Size Premium, Value Premium, Stock Splits, Equity Premium Puzzle, Anchoring and Adjustment Heuristic, CAPM, Asset Pricing, Accrual Anomaly, Low Volatility Anomaly, Low-beta-high- alpha, Momentum Effect JEL Classification: G12, G11, G02 1 Resurrecting the Capital Asset Pricing Model It is fair to trace the birth of asset pricing theory to the capital asset pricing model (CAPM) of Sharpe (1964) and Lintner (1965). Over five decades later, CAPM is still the most widely used model in practice. However, academic finance has largely moved away from CAPM due to the discovery of a large number of phenomena that are generally considered to be inconsistent with the model.1 Such empirical difficulties have led Fama and French (1992) (and others) to claim that the CAPM is dead. In this article, I show that it is theoretically possible to internalize almost all of the prominent anomalies if a pragmatic approach to approximating optimal Bayesian inference is incorporated in the model. Hence, the conclusion that the CAPM is dead is premature. The key principle on which financial decisions turn is the relationship between risk and return. How are beliefs about risks formed? In general, a large number of factors contribute to risk in any given situation. Consider any given firm. A large number of factors (such as industry structure, regulations, labor relations, technology, input supply constraints, business strategy, and investment policy) matter for the volatility of its stock. There are nearly 5000 firms listed in the New York stock exchange alone, so optimal Bayesian inference requiring an accurate assessment of all the relevant factors for every firm is intractable. The problem becomes more manageable with the realization that many factors are sector-specific, that is, are common to every firm in the same sector. So, instead of re-inventing the wheel for every firm, a pragmatic approach is to leverage such commonalities by using the sector-specific factors to furnish an informative starting point and then attempting to make appropriate adjustments pertaining to individual firms in the same sector. This is the approach taken by brokerage houses, commercial banks, and investment banks, as they typically employ sector specialists who focus on a group of firms in the same sector. To take a concrete example, suppose adverse weather conditions are affecting the supply of coffee beans. Clearly, this is a factor that matters for all coffee producers. A pragmatic approach is to analyze the impact of adverse weather conditions on the sector leader (about which information is readily available) and use it as an informative starting point for other firms. 1 Two prominent CAPM anomalies are size and value effects. Size effect is documented in Banz (1981), Reinganum (1983), Brown et al (1983), and more recently in Hou, Xue, and Zhang (2014), and Fama and French (2015) among many others. Value premium is documented in Fama and French (1998) among many others. 2 This informative starting points needs to be adjusted as other firms may have hedged differently in the futures market, may hold different levels of inventory, and have varying relations with suppliers among other factors. This pragmatic approach has the added advantage of making it likely that an analyst would at least be qualitatively correct in ranking the firms even if he gets the magnitudes wrong. Unsurprisingly, Da and Schaumburg (2011) find that equity analysts are consistently able to rank stocks correctly making them qualitatively or rank-order correct even though they are often quantitatively incorrect. In this article, I study the implications of incorporating this pragmatic approach into CAPM. The surprising finding is that it gives rise to a unified theoretical explanation for almost all of the prominent anomalies concerning CAPM. Without asserting that anomalies are completely resolved, which requires a comprehensive empirical examination of a large number of phenomena, and so is beyond the scope of any single article, this article shows that the reliance on the pragmatic approach must be considered as an alternative explanation before rejecting CAPM. In this respect, the article paves the way for such empirical testing by explicitly deriving CAPM formula, adjusted for reliance on the pragmatic approach, form first principles. In practice, CAPM is also widely used in calculating the cost of equity and in evaluating the performance of managed portfolios. This practice is considered problematic due to various anomalies facing CAPM (Fama and French 2004). As integrating the pragmatic approach with CAPM internalizes the anomalies, immediate applications of the adjusted CAPM are improved estimation of cost of equity and improved evaluation of portfolio performance. This article is organized as follows. Section 1 discusses the importance of informative starting points in decision-making. Section 2 and 3 derive CAPM adjusted for reliance on informative starting points. Section 4 shows how various prominent anomalies are internalized. Section 5 discusses the improved calculation of cost and equity and improved evaluation of managed portfolios with the adjusted CAPM. Section 6 concludes. 1. Reliance on Informative Starting Points Bayesian inference provides a unified framework for making decisions as new information arrives. However, outside of the simplest of situations, exact Bayesian inference is intractable, and must be approximated. Relying on informative starting points that are somewhat incorrect 3 and attempting to adjust them appropriately is a pragmatic solution, which is considered an optimal response of a Bayesian decision-maker facing finite computational resources (Lieder, Griffiths, & Goodman 2013). Evidence of the anchoring-and-adjustment process has been found in brain imaging studies demonstrating that we are hard-wired to rely on informative starting points and then attempting to adjust them (Quo, Zhao, and Luo 2008). It is intractable for anyone to accurately measure all of the risk factors, which is what needs to be done, in order to make the optimal decision. A pragmatic approach is considering the factors that one can assess, and using them to furnish an informative starting point (anchor), and then attempting to adjust the starting point appropriately. Such anchoring-and-adjustment is a robust human decision-making heuristic. Describing the anchoring heuristic, Epley and Gilovich write (2001), “People may spontaneously anchor on information that readily comes to mind and adjust their response in a direction that seems appropriate, using what Tversky and Kahneman (1974) called the anchoring and adjustment heuristic. Although this heuristic is often helpful, the adjustments tend to be insufficient, leaving people’s final estimates biased towards the initial anchor value.” (Epley and Gilovich (2001) page. 1). It is easy to provide several examples of such reliance on informative starring points. When respondents were asked which year George Washington became the first US President, most would start from the year the US became a country (in 1776). They would reason that it might have taken a few years after that to elect the first president so they add a few years to 1776 to work it out, coming to an answer of 1778 or 1779. George Washington actually became president in 1789, implying that, starting from 1776, adjustments are typically insufficient. Another example is the freezing temperature of vodka. People typically know that vodka freezes at a temperature below the freezing point of water (0 Celsius). So, when asked about the freezing point of vodka, they tend to start from the freezing point of water and then adjust downwards to form an estimate. However, their adjustments do not go far enough, and fall short of the right answer (which is -24 Celsius). The adjustments tend to stop once a plausible value is reached leaving the final answer biased towards the starting value (Epley and Gilovich 2006). Hirshleifer (2001) considers anchoring-and-adjustment to be an “important part of psychology based dynamic asset pricing theory in its infancy” (p. 1535). Shiller (1999) argues that anchoring appears to be an important concept for financial markets. This argument has been supported quite strongly by recent empirical research on financial markets. Anchoring-and-adjustment has been found to matter for credit spreads that banks charge to firms (Douglas et al 2015), it matters in determining the price of target firms in mergers and acquisitions (Baker et al 2012), and it also 4 affects the earnings forecasts made by analysts in the stock markets (Cen et al 2013). Furthermore, Siddiqi (2015) shows that anchoring-and-adjustment provides a unified explanation for a number
Load more

Recommended publications
  • Reverse Stock Split Faq
    REVERSE STOCK SPLIT FAQ 1 What is a reverse stock split? A reverse stock split involves replacing, by exchange, a certain number of old shares (in the present case, 20) for one new share, without altering the amount of the company's capital. In practice such an operation creates the following mechanical effects: - the number of new shares in circulation on the market is reduced proportionally to the exchange ratio (several old shares are transformed into one new share); - the par value, and as a consequence, the market price, of each new share are raised proportionally to the exchange ratio. What is the goal of this reverse stock split? The reverse stock split forms part of Soitec’s desire to support its renewed profitable growth momentum, having refocused on its core electronics business. Moreover, the reverse stock split may reduce the volatility of the price of Soitec share caused by its current low price level. What is the proposed exchange ratio for this reverse stock split? The exchange ratio is 1 for 20. In other words, one new share with par value of €2.00 will be exchanged for 20 old shares with par value of €0.10. Why was this 1:20 ratio chosen? This exchange ratio has been chosen for the purpose of positioning the new shares in the average of the values of the shares listed on Euronext. When will the reverse stock split be effective? In accordance with the notice published in the Bulletin des Annonces Légales Obligatoires on 23 December 2016, the reverse stock split will take effect on 8 February 2017, i.e.
    [Show full text]
  • The Future of Computer Trading in Financial Markets an International Perspective
    The Future of Computer Trading in Financial Markets An International Perspective FINAL PROJECT REPORT This Report should be cited as: Foresight: The Future of Computer Trading in Financial Markets (2012) Final Project Report The Government Office for Science, London The Future of Computer Trading in Financial Markets An International Perspective This Report is intended for: Policy makers, legislators, regulators and a wide range of professionals and researchers whose interest relate to computer trading within financial markets. This Report focuses on computer trading from an international perspective, and is not limited to one particular market. Foreword Well functioning financial markets are vital for everyone. They support businesses and growth across the world. They provide important services for investors, from large pension funds to the smallest investors. And they can even affect the long-term security of entire countries. Financial markets are evolving ever faster through interacting forces such as globalisation, changes in geopolitics, competition, evolving regulation and demographic shifts. However, the development of new technology is arguably driving the fastest changes. Technological developments are undoubtedly fuelling many new products and services, and are contributing to the dynamism of financial markets. In particular, high frequency computer-based trading (HFT) has grown in recent years to represent about 30% of equity trading in the UK and possible over 60% in the USA. HFT has many proponents. Its roll-out is contributing to fundamental shifts in market structures being seen across the world and, in turn, these are significantly affecting the fortunes of many market participants. But the relentless rise of HFT and algorithmic trading (AT) has also attracted considerable controversy and opposition.
    [Show full text]
  • Tony Ramirez, Et Al. V. Marathon Patent Group Inc, Et Al. 18-CV
    Case 2:18-cv-06309-FMO-PLA Document 1 Filed 07/20/18 Page 1 of 11 Page ID #:1 Adam C. McCall (SBN 302130) 1 [email protected] 2 LEVI & KORSINSKY, LLP 445 South Figueroa Street, 31st Floor 3 Los Angeles, California 90025 4 Telephone: (213) 985-7290 5 Facsimile: (202) 333-2121 6 Attorneys for Plaintiff 7 [Additional counsel on signature page] 8 9 UNITED STATES DISTRICT COURT 10 11 CENTRAL DISTRICT OF CALIFORNIA 12 TONY RAMIREZ, ) Case No. 18-cv-06309 13 ) Plaintiff, ) CLASS ACTION COMPLAINT FOR 14 vs. ) VIOLATIONS OF FEDERAL 15 ) SECURITIES LAWS MARATHON PATENT GROUP INC., ) 16 DOUG CROXALL, EDWARD KOVALIK, ) JURY TRIAL DEMANDED 17 CHRISTOPHER ROBICHAUD, ) RICHARD TYLER, AND RICHARD ) 18 CHERNICOFF, ) 19 ) Defendants. ) 20 ) 21 22 23 24 25 26 27 28 30 31 32 Case 2:18-cv-06309-FMO-PLA Document 1 Filed 07/20/18 Page 2 of 11 Page ID #:2 1 Plaintiff Tony Ramirez (“Plaintiff”), by his undersigned attorneys, alleges the following 2 on information and belief, except as to those allegations pertaining to its own knowledge and 3 conduct, which is made on personal knowledge: 4 INTRODUCTION 5 1. Plaintiff asserts this action for violating federal securities laws to remedy false 6 and misleading disclosures made by Marathon Patent Group Inc. (“Marathon” or the 7 “Company”) and its Board of Directors (the “Board) in a proxy statement issued in connection 8 with the Company’s 2017 annual meeting of stockholders (the “Annual Meeting”). 9 2. On June 8, 2017, the Company filed a Schedule 14A Proxy Statement (the 10 “Proxy”) with the Securities and Exchange Commission (the “SEC”) for the Annual Meeting.
    [Show full text]
  • Stock Split Quick Tips
    Stock Splits Quick tip This “Quick tip” highlights how stock splits affect grants received through your company’s equity awards program. (Please refer to your official plan documents for the specific terms of your awards.) What is a stock split? A stock split is when a company issues additional shares of its stock to current stockholders. With a 2-for-1 stock split, for example, current shareholders receive one additional share for each share they hold as of the record date. When a company splits its stock, it has more shares outstanding. But its market value does not increase, as the price of its stock (after the split) reflects those additional shares. In the case of a 2-for-1 stock split, the stock price after the split would be half the price before the split (not including any normal market fluctuations). Generally, a company will split its stock to make its stock price appear more affordable to individual investors, as the share price after the split will be lower than before the split. How a stock split affects equity awards A stock split does not directly affect the potential value of any equity awards received through your company’s plan. However, both the grant price of a stock option and the number of stock options (or other awards) will be adjusted to reflect the split. This adjustment is made automatically; there is nothing you need to do. Here’s a stock option example, using a 2-for-1 stock split. Here’s a restricted award example, again using a 2-for-1 stock The number of options is adjusted upwards and the grant split.
    [Show full text]
  • Refinitiv Corporate Actions Methodology
    REFINITIV EQUITY INDICES Corporate Action Methodology April 2020 Published: April 6, 2020 © 2019 Refinitiv Limited. All Rights Reserved. Refinitiv Limited, by publishing this document, does not guarantee that any information contained herein is or will remain accurate or that use of the information will ensure correct and faultless operation of the relevant service or associated equipment. Neither Refinitiv Limited, nor its agents or employees, shall be held liable to any user or end user for any loss or damage (whether direct or indirect) whatsoever resulting from reliance on the information contained herein. This document may not be reproduced, disclosed, or used in whole or part without the prior written consent of Refinitiv. 1 Sensitivity: Confidential Contents Introduction ......................................................................................................................................... 3 Corporate Actions ............................................................................................................................... 4 1.1 Cash Dividend .......................................................................................................................... 4 1.2 Special Dividend ...................................................................................................................... 5 1.3 Cash Dividend with Stock Alternative ....................................................................................... 5 1.4 Stock Dividend ........................................................................................................................
    [Show full text]
  • Accessing the U.S. Capital Markets
    ACCESSING THE U.S. CAPITAL MARKETS SECURITIES PRODUCTS An Introduction to United States Securities Laws This and other volumes of Accessing the U.S. Capital Markets have been prepared by Sidley Austin LLP for informational purposes only, and neither this volume nor any other volume constitutes legal advice. The information contained in this and other volumes is not intended to create, and receipt of this or any other volume does not constitute, a lawyer-client relationship. Readers should not act upon information in this or any other volume without seeking advice from professional advisers. Sidley Austin LLP, a Delaware limited liability partnership which operates at the firm’s offices other than Chicago, London, Hong Kong, Singapore and Sydney, is affiliated with other partnerships, including Sidley Austin LLP, an Illinois limited liability partnership (Chicago); Sidley Austin LLP, a separate Delaware limited liability partnership (London); Sidley Austin LLP, a separate Delaware limited liability partnership (Singapore); Sidley Austin, a New York general partnership (Hong Kong); Sidley Austin, a Delaware general partnership of registered foreign lawyers restricted to practicing foreign law (Sydney); and Sidley Austin Nishikawa Foreign Law Joint Enterprise (Tokyo). The affiliated partnerships are referred to herein collectively as “Sidley Austin LLP,” “Sidley Austin” or “Sidley.” This volume is available electronically at www.accessingsidley.com. If you would like additional printed copies of this volume, please contact one of our lawyers or our Marketing Department at 212-839-5300, e-mail: [email protected]. For further information regarding Sidley Austin, you may access our web site at www.sidley.com Our web site contains address, phone and e-mail information for our offices and attorneys.
    [Show full text]
  • The Analisys Impact of Stock Split and Reverse Stock Split on Stock Return and Volume the Case of Jakarta Stock Exchange
    THE ANALISYS IMPACT OF STOCK SPLIT AND REVERSE STOCK SPLIT ON STOCK RETURN AND VOLUME THE CASE OF JAKARTA STOCK EXCHANGE Melinda Savitri and Dwi Martani* The research examines the impact of stock split and reverse stock split on stock return and trading volume on Jakarta Stock Exchange betweens 2001-2005. We analyze abnormal returns and volume during windows period around the split and relate stocks returns to profitability, leverage and volume.. We find that there is a significant abnormal return on the date of split on the fifth day before split. On the reverse stock split, there is a significant abnormal return between third days before to first day after split. The results reveal that reverse stock split have more effect to the stock return than stock split. There is a significant volume difference between the days before and after the stock split or reverse stock split Trading volume and return on asset have significant influence on market adjusted return but debt to equity ratio is not significant. Key word: market return, trading volume, stock split, reverse stock split Field Research: FINANCE For the past five years, there has been numbers of corporate actions affecting stock price that has had happened in Jakarta Stock Exchange (JSX). The conduct of stock split or reverse stock split may merely be cosmetic and is done only when the company wishes to increase or decrease its stock price. But often at times, during days before or after stock split or reverse stock split, there are irregular phenomenon found related to abnormal returns, liquidity, and volatility.
    [Show full text]
  • Report of Organizational Actions Affecting Basis of Securities
    Report of Organizational Actions Form 8937 (December 2017) Affecting Basis of Securities OMB No. 1545-0123 Department of the Treasury Internal Revenue Service ~See separate Instructions. Issuer 1 Issuer's name 2 Issuer's employer Identificationnumber (EIN} PIMCO CommoditiesPLUS• Strate Fund 27-2067579 3 Name of contact for addillonal Information 4 Telephone No. of contact 5 Email address of contact Erik Brown 888 877-4626 lmrunds@dsts stems.com 6 Number and street (or P.O. box If mall ls not delivered to street address) of contact 7 City, town, or post office, state, and ZIP code of contact 1633 Broadwa New York NV 10019 8 Date of action 9 Classification and description March 26 2021 Common Stock of a Re ulated Investment Com an 10 CUSIP number 11 Serial number(s) 12 Ticker symbol 13 Account number(s) Various - See attached Various - See attached Or anizational Action Attach additional statements if needed. See back of form for additional questions. 14 Describe the organizational action and, If applicable, the date of the action or the date against which shareholders' ownership is measured for the action~ On March 26, 2021, PIMCO Commodity RealReturn Strategy Fund effected a one-for-two reverse split or all classes or its outstanding common stock. 15 Describe the quantitative effect of the organizational action on the basis of the security In the hands of a U.S. taxpayer as an adjustment per share or as a percentage of old basis~ Under Internal Revenue Code (IRC) Section 305(a), the reverse stock split is a nontaxable transaction.
    [Show full text]
  • Form 8-K Northern Oil and Gas, Inc
    UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 8-K CURRENT REPORT Pursuant to Section 13 or 15(d) of the Securities Exchange Act of 1934 Date of Report (Date of earliest event reported): September 18, 2020 NORTHERN OIL AND GAS, INC. (Exact name of Registrant as specified in its charter) Delaware 001-33999 95-3848122 (State or other jurisdiction (Commission File Number) (IRS Employer of incorporation) Identification No.) 601 Carlson Parkway, Suite 990 Minnetonka, Minnesota 55305 (Address of principal executive offices) (Zip Code) Registrant’s telephone number, including area code (952) 476-9800 Check the appropriate box below if the Form 8-K filing is intended to simultaneously satisfy the filing obligation of the registrant under any of the following provisions: Written communications pursuant to Rule 425 under the Securities Act (17 CFR 230.425) Soliciting material pursuant to Rule 14a-12 under the Exchange Act (17CFR 240.14a-12) Pre-commencement communications pursuant to Rule 14d-2(b) under the Exchange Act (17 CFR 240.14d-2(b)) Pre-commencement communications pursuant to Rule 13e-4(c) under the Exchange Act (17 CFR 240.13e-4(c)) Securities registered pursuant to Section 12(b) of the Act: Title of each class Trading Symbol(s) Name of each exchange on which registered Common Stock, par value $0.001 NOG NYSE American Indicate by check mark whether the registrant is an emerging growth company as defined in Rule 405 of the Securities Act of 1933 (§230.405 of this chapter) or Rule 12b-2 of the Securities Exchange Act of 1934 (§240.12b-2 of this chapter).
    [Show full text]
  • Stock Split and Its Impact on Stock Market – Evidence from Indian Stocks Dr
    Sen Swapna; International Journal of Advance Research, Ideas and Innovations in Technology ISSN: 2454-132X Impact factor: 4.295 (Volume 4, Issue 3) Available online at: www.ijariit.com Stock split and its impact on stock market – Evidence from Indian stocks Dr. Swapna Sen [email protected] Jagannath International Management School, Kalkaji, New Delhi ABSTRACT The study attempted to assess the impact of the stock split on the stock price, volatility, and liquidity. To do this a sample of 365 companies are considered which has undergone split during the period 2011 to 2017. The paired t-test is carried out for pre and post values of Mean Return, Volatility, Beta, Sharpe’s Ratio, Treynor Ratio, CAPM Return, Abnormal Return, and Liquidity to assess the impact of the split event on the stock performance. Overall results say that there is a drop in stock returns and increase in volatility after the split. There is no significant change in liquidity with the split. But when the analysis is done separately for costly and cheap stocks, it revealed that for costly stocks, there is the drop in returns, there is no further worsening of volatility and significant improvement in liquidity post-split. Thus split is effective to some extent only for costly stocks in terms of increase in the volume of trades after the split. Otherwise, this corporate action is not of any positive impact on wealth creation, volatility or liquidity. Keywords: Stock split, Volatility, Liquidity, CAPM return, Abnormal return, Beta 1. INTRODUCTION A stock split is a corporate action in which a company divides its existing shares into multiple shares.
    [Show full text]
  • Anchoring Adjusted Capital Asset Pricing Model
    Munich Personal RePEc Archive Anchoring Adjusted Capital Asset Pricing Model Hammad, Siddiqi The University of Queensland 1 October 2015 Online at https://mpra.ub.uni-muenchen.de/67403/ MPRA Paper No. 67403, posted 22 Oct 2015 17:30 UTC Anchoring Adjusted Capital Asset Pricing Model Hammad Siddiqi The University of Queensland Australia [email protected] October 2015 Abstract An anchoring adjusted Capital Asset Pricing Model (ACAPM) is developed in which the payoff volatilities of well-established stocks are used as starting points that are adjusted to form volatility judgments about other stocks. Anchoring heuristic implies that such adjustments are typically insufficient. ACAPM converges to CAPM with correct adjustment, so CAPM is a special case of ACAPM. The model provides a unified explanation for the size, value, and momentum effects in the stock market. A key prediction of the model is that the equity premium is larger than what can be justified by market volatility. Hence, anchoring also provides a potential explanation for the well- known equity premium puzzle. Anchoring approach predicts that stock splits are associated with positive abnormal returns and an increase in return volatility. The approach predicts that reverse stock-splits are associated with negative abnormal returns, and a fall in return volatility. Existing empirical evidence strongly supports these predictions. Keywords: Size Premium, Value Premium, Behavioral Finance, Stock Splits, Equity Premium Puzzle, Anchoring Heuristic, CAPM, Asset Pricing JEL Classification: G12, G11, G02 1 Anchoring Adjusted Capital Asset Pricing Model Finance theory predicts that risk adjusted returns from all stocks must be equal to each other. The starting point for thinking about the relationship between risk and return is the Capital Asset Pricing Model (CAPM) developed in Sharpe (1964), and Lintner (1965).
    [Show full text]
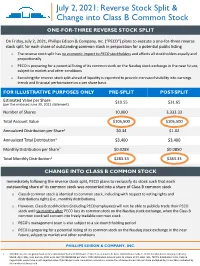
  • July 2, 2021: Reverse Stock Split & Change Into Class B Common Stock
    July 2, 2021: Reverse Stock Split & Change into Class B Common Stock ONE-FOR-THREE REVERSE STOCK SPLIT On Friday, July 2, 2021, Phillips Edison & Company, Inc. (“PECO”) plans to execute a one-for-three reverse stock split for each share of outstanding common stock in preparation for a potential public listing o The reverse stock split has no economic impact to PECO stockholders and affects all stockholders equally and proportionally o PECO is preparing for a potential listing of its common stock on the Nasdaq stock exchange in the near future, subject to market and other conditions o Executing the reverse stock split ahead of liquidity is expected to provide increased visibility into earnings trends and financial performance on a per share basis FOR ILLUSTRATIVE PURPOSES ONLY PRE-SPLIT POST-SPLIT Estimated Value per Share $10.55 $31.65 (per the enclosed June 30, 2021 statement) Number of Shares 10,000 3,333.33 Total Account Value $105,500 $105,500 Annualized Distribution per Share1 $0.34 $1.02 Annualized Total Distribution1 $3,400 $3,400 Monthly Distribution per Share1 $0.0283 $0.0850 Total Monthly Distribution1 $283.33 $283.33 CHANGE INTO CLASS B COMMON STOCK Immediately following the reverse stock split, PECO plans to reclassify its stock such that each outstanding share of its common stock was converted into a share of Class B common stock o Class B common stock is identical to common stock, including with respect to voting rights and distributions rights (i.e., monthly distributions) o However, Class B stockholders (including PECO employees) will not be able to publicly trade their PECO stock until six months after PECO lists its common stock on the Nasdaq stock exchange, when the Class B common stock will convert into freely tradable common stock o PECO’s management team is also subject to a six-month holding period o PECO is preparing for a potential listing of its common stock on the Nasdaq stock exchange in the near future, subject to market and other conditions PHILLIPS EDISON & COMPANY, INC.
    [Show full text]