How to Hit Home Runs: Optimum Baseball Bat Swing Parameters for Maximum Range Trajectories Gregory S
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rules & Regulations
YOUTH BASEBALL RULES & REGULATIONS HOUSE PROGRAM Tee-Ball 1: Maverick, Stallion & Mustang: Ages 4-5 (Pre-school): Ages 9-12 (Grades 3-6): Plays during the spring of the year prior to entry into Age groups are combined and players are drafted by kindergarten. Kids hit the ball off of a tee, no catcher, ability based on a player evaluation. Teams are mixed and a dad occupies 1st base. Everyone plays the field, up with players from multiple schools. Kids pitch all everyone bats. 6 innings and umpires are utilized for the first time. Playoffs at the end of the season determine a league • Teams are divided up by school champion. • One practice per week • 10 game season Maverick and Stallion are competitive leagues where • Games played at Glen Crest/Parkview/Village stealing is allowed after the ball crosses the plate. Green Park Mustang is a competitive league where full baseball Tee-Ball 2: rules apply, including leadoffs, stealing and dropped Age 6 (Kindergarten): third strikes. Kids hit off a tee but by the end of the year, a coach • Teams are mixed up with players from multiple may pitch the ball from a few feet away. Kids play 1st schools based on ability. base for the first time, no catcher, everyone plays the • 14 game season (2-3 games per week). Double field and bats. elimination post season tournament • Teams are divided up by school • Games played at Village Green Park LEAGUES • One practice per week • 10 game season Leagues may be combined or eliminated depending • Games played at Glen Crest/Parkview/Village on enrollment. -

Glynn County Recreation and Parks Department Proposed Youth Baseball Rules and Regulations 2019
GLYNN COUNTY RECREATION & PARKS DEPARTMENT Athletics Division 323 Old Jesup Road; Brunswick, Georgia 31520 (912) 554 – 7780 / Fax: (912) 267 – 5744 Our Mission: To provide quality, year round recreational activities, facilities, and services that are safe, fun, and enhance the quality of life for all Glynn County citizens. Glynn County Recreation and Parks Department Proposed Youth Baseball Rules and Regulations 2019 Governing Authority 1. The Manager of the GCRPD reserves the right to all final decisions. 2. The official rules of the Georgia High School Association and GRPA will be used in all leagues except those noted in the General Rules and League Rules. General League Rules st 1. The age control date for youth baseball is prior to September 1 , 2019. 2. The age divisions for youth baseball are as follows: 7-8 Farm League 9-10 Mites 11-12 Midgets 13-14 Juniors 15-17 Seniors 3. All players that are present for game will be inserted in the scorebook and must bat in that order for the entire game. 4. Players arriving late for a game will be inserted at the bottom of the batting order and will be inserted into the rotation as soon as possible. 5. A game may be started with eight (8) players. The game will be a forfeit if there are less than eight (8) players present. If both teams have less than eight (8) players both teams will forfeit. If a team begins a game with eight (8) players, they must take an out in the ninth (9th) spot of the batting order until/if that player arrives to fill the spot. -

Physics of Knuckleballs
Home Search Collections Journals About Contact us My IOPscience Physics of knuckleballs This content has been downloaded from IOPscience. Please scroll down to see the full text. 2016 New J. Phys. 18 073027 (http://iopscience.iop.org/1367-2630/18/7/073027) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 129.104.29.1 This content was downloaded on 03/08/2016 at 09:50 Please note that terms and conditions apply. New J. Phys. 18 (2016) 073027 doi:10.1088/1367-2630/18/7/073027 PAPER Physics of knuckleballs OPEN ACCESS Baptiste Darbois Texier1, Caroline Cohen1, David Quéré2 and Christophe Clanet1,3 RECEIVED 1 LadHyX, UMR 7646 du CNRS, Ecole Polytechnique, 91128 Palaiseau Cedex, France 18 December 2015 2 PMMH, UMR 7636 du CNRS, ESPCI, 75005 Paris, France REVISED 3 Author to whom any correspondence should be addressed. 6 June 2016 ACCEPTED FOR PUBLICATION E-mail: [email protected] 20 June 2016 Keywords: sport ballistics, zigzag trajectory, path instability, drag crisis, symmetry breaking PUBLISHED 13 July 2016 Original content from this Abstract work may be used under Zigzag paths in sports ball trajectories are exceptional events. They have been reported in baseball the terms of the Creative Commons Attribution 3.0 (from where the word knuckleball comes from), in volleyball and in soccer. Such trajectories are licence. associated with intermittent breaking of the lateral symmetry in the surrounding flow. The different Any further distribution of this work must maintain scenarios proposed in the literature (such as the effect of seams in baseball) are first discussed and attribution to the author(s) and the title of compared to existing data. -

Describing Baseball Pitch Movement with Right-Hand Rules
Computers in Biology and Medicine 37 (2007) 1001–1008 www.intl.elsevierhealth.com/journals/cobm Describing baseball pitch movement with right-hand rules A. Terry Bahilla,∗, David G. Baldwinb aSystems and Industrial Engineering, University of Arizona, Tucson, AZ 85721-0020, USA bP.O. Box 190 Yachats, OR 97498, USA Received 21 July 2005; received in revised form 30 May 2006; accepted 5 June 2006 Abstract The right-hand rules show the direction of the spin-induced deflection of baseball pitches: thus, they explain the movement of the fastball, curveball, slider and screwball. The direction of deflection is described by a pair of right-hand rules commonly used in science and engineering. Our new model for the magnitude of the lateral spin-induced deflection of the ball considers the orientation of the axis of rotation of the ball relative to the direction in which the ball is moving. This paper also describes how models based on somatic metaphors might provide variability in a pitcher’s repertoire. ᭧ 2006 Elsevier Ltd. All rights reserved. Keywords: Curveball; Pitch deflection; Screwball; Slider; Modeling; Forces on a baseball; Science of baseball 1. Introduction The angular rule describes angular relationships of entities rel- ative to a given axis and the coordinate rule establishes a local If a major league baseball pitcher is asked to describe the coordinate system, often based on the axis derived from the flight of one of his pitches; he usually illustrates the trajectory angular rule. using his pitching hand, much like a kid or a jet pilot demon- Well-known examples of right-hand rules used in science strating the yaw, pitch and roll of an airplane. -

Role of Materials & Design on Performance of Baseball Bats
Copyright Warning & Restrictions The copyright law of the United States (Title 17, United States Code) governs the making of photocopies or other reproductions of copyrighted material. Under certain conditions specified in the law, libraries and archives are authorized to furnish a photocopy or other reproduction. One of these specified conditions is that the photocopy or reproduction is not to be “used for any purpose other than private study, scholarship, or research.” If a, user makes a request for, or later uses, a photocopy or reproduction for purposes in excess of “fair use” that user may be liable for copyright infringement, This institution reserves the right to refuse to accept a copying order if, in its judgment, fulfillment of the order would involve violation of copyright law. Please Note: The author retains the copyright while the New Jersey Institute of Technology reserves the right to distribute this thesis or dissertation Printing note: If you do not wish to print this page, then select “Pages from: first page # to: last page #” on the print dialog screen The Van Houten library has removed some of the personal information and all signatures from the approval page and biographical sketches of theses and dissertations in order to protect the identity of NJIT graduates and faculty. ABSTRACT ROLE OF MATERIAL & DESIGN ON PERFORMANCE OF BASEBALL BATS by Kim Benson-Worth Baseball bat safety has become an increasing area of interest with more than 19 million people in the United States alone participating in this sport. An increase in injuries resulting from bat injuries has brought the performance of the bats into question. -

Lessons You Can Learn by Watching a Game
Lessons You Can Learn by Watching a Game Good coaches no matter how old they are will watch a game and come away learning something. Even if they may be watching the game for enjoyment, there is always something they will see that could possibly help them in the future. A great teaching moment is to take your team to a game or watch a game on TV with them. Show your players during that game not only the good things that are happening but also the things that are done that may cost a run and eventually a game. Coaches can teach their players what to look for during the game like offensive and defensive weaknesses and tendencies. They can teach situations that come up during the game and can teach why something worked or why it didn’t work. Pictures are worth a thousand words. Even watching Major League Baseball games on TV will provide a lot of teachable moments. Lesson One: When Jason Wurth hit the winning walk off home run in the ninth inning during game four against the Cardinals, the Nationals went wild. Yes, it was a big game to win but it was not the Championship game. Watching them storm the field and jump up and down with excitement, made me shake my head. I have been on both sides of that scenario and that becomes bulletin board material. The Cardinals came back to win the next game and take the series. Side note: in case you have never heard that term, bulletin board material means that a player/team said or did something that could make the other team irritated at them to the point that it inspires that other team to do everything possible to beat the team. -

Here Comes the Strikeout
LEVEL 2.0 7573 HERE COMES THE STRIKEOUT BY LEONARD KESSLER In the spring the birds sing. The grass is green. Boys and girls run to play BASEBALL. Bobby plays baseball too. He can run the bases fast. He can slide. He can catch the ball. But he cannot hit the ball. He has never hit the ball. “Twenty times at bat and twenty strikeouts,” said Bobby. “I am in a bad slump.” “Next time try my good-luck bat,” said Willie. “Thank you,” said Bobby. “I hope it will help me get a hit.” “Boo, Bobby,” yelled the other team. “Easy out. Easy out. Here comes the strikeout.” “He can’t hit.” “Give him the fast ball.” Bobby stood at home plate and waited. The first pitch was a fast ball. “Strike one.” The next pitch was slow. Bobby swung hard, but he missed. “Strike two.” “Boo!” Strike him out!” “I will hit it this time,” said Bobby. He stepped out of the batter’s box. He tapped the lucky bat on the ground. He stepped back into the batter’s box. He waited for the pitch. It was fast ball right over the plate. Bobby swung. “STRIKE TRHEE! You are OUT!” The game was over. Bobby’s team had lost the game. “I did it again,” said Bobby. “Twenty –one time at bat. Twenty-one strikeouts. Take back your lucky bat, Willie. It was not lucky for me.” It was not a good day for Bobby. He had missed two fly balls. One dropped out of his glove. -

Baseball Social Distancing: • Practice – Coaches Are Responsible for Ensuring Social Distancing Is Maintained Between Players As Much As Possible
Baseball Social distancing: • Practice – Coaches are responsible for ensuring social distancing is maintained between players as much as possible. This means additional spacing between players while playing chatting, changing drills so that players remain spaced out, and no congregating of players while waiting to bat. Workouts should be conducted in ‘pods’ of students, with the same 5-10 students always working out together. This ensures more limited exposure if someone develops an infection. • Dugouts – No dugouts should be used during practice. Players’ items should be lined up outside and against the fence at least six feet apart. Dugouts should be permitted only during games, and may be extended, by NFHS rule, down the foul lines outside the playing area to allow for social distancing. Additionally, bleachers can be placed directly behind the dugouts for additional seating for team personnel. Players should maintain social distancing unless they are actively participating in the game. • Field of Play – Only essential personnel are permitted on the field of play. These are defined as players, coaches, athletic trainers, and umpires. All others, i.e., ball/bat shaggers, managers, statisticians, pitch count designees, media photographers, etc. are considered non-essential personnel and are not to be in the dugout or extended dugout area. • Spectators – Schools must limit the use of bleachers for fans. Schools should encourage fans to bring their own chairs or stand. Fans should practice social distancing between different household units and accept personal responsibility for public health guidelines. • Media – All local social distancing and hygiene guidelines for spectators should be followed by media members planning to attend games. -
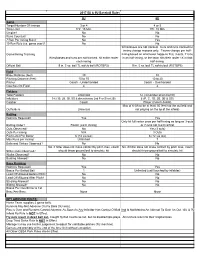
No No Runs Counted? No No 7 Run Per Inning Rule? No Yes 10 Run Rule (I.E
2017 5U & 6U Baseball Rules 5U 6U Game Target Number Of Innings 3 or 4 4 or 5 Time Limit 1Hr. 15 Min. 1Hr. 15 Min. Umpire? No No Runs Counted? No No 7 Run Per Inning Rule? No Yes 10 Run Rule (i.e. game over)? No No Wins/losses are not tracked. Outs and runs tracked for inning change reasons only. Teams change per half- Game/Inning Tracking inning based on whichever happens first, 3-outs, 7 runs Wins/losses and runs are not tracked, hit entire roster in an half-inning, or the team hits their roster 1X in that each inning half-inning. Official Ball 9 in. 5 oz. ball TL safety ball (ROTBP5) 9 in. 5 oz. ball TL safety ball (ROTBP5) Field Base Distance (feet) 40 40 Pitching Distance (feet) 10 to 15 10 to 20 Pitcher Coach - Underhanded Coach - Overhanded Coaches On Field 4 4 Fielders Total Fielders Unlimited 12 (remainder sit on bench) Infielders 5-6 (1B, 2B, 3B, SS & discretionary 2nd P or Short 2B) 6 (P, C, 1B, 2B, 3B & SS) Catcher Coach Player (Coach Assist) Max of 6 (Must be at least 30 feet into the outfield and Outfielders Unlimited not playing on the lip of the infield) Batting Helmets Required? Yes Yes Only hit full roster once per half-inning as long as 3-outs Batting Order? Roster (each inning) or 7-runs not reached first Outs Observed? No Yes (3 outs) Outs Per Inning N/A 3 Outs Pitch Limit Per Batter 6 (+2 via tee) 6 (+2 via tee) Max Runs per inning? Unlimited 7 Balls and Strikes Observed? No No No, if hitter does not make contact by pitch max, coach No, if hitter does not make contact by pitch max, coach Strike Outs Observed? should throw ground ball to simulate hit should throw ground ball to simulate hit Walks Observed? No No Bunting Allowed? No No Base Running Helmets Required? Yes Yes Bases Per Batted Ball 1 Unlimited (until touched by infielder) Lead Off Allowed Before Pitch? No No Lead Off Allowed After Pitch? No No Stealing Allowed? No No Sliding Allowed? No No Bases Per Overthrow to 1st Base/Any Base None None KEY GROUND RULES: Home Team supplies 2 game balls. -

2018 Baseball Format
2018 BASEBALL FORMAT SPORT SPECIFIC INFORMATION BASEBALL COMMITTEE MEMBERS Dist. A Mr. Tom Murphy, Principal, Billerica Dist. F Mr. Anthony Papuga, Assistant Principal Memorial HS Pathfinder High School Mr. Tom O’Brien, Athletic Director Mr. Don Irzyk, Athletic Director Haverhill High School Pathfinder High School Dist. B Mr. Phil Brangiforte, Headmaster Dist. G Mr. Henry Duval, Assistant Principal East Boston High School Pittsfield High School Mr. Michael Lahiff, Athletic Director Mr. Jim Abel, Athletic Director Watertown High School Pittsfield High School Dist. C Mr. Marc Talbot, Principal Dist. H Mr. Patrick Driscoll , Athletic Director Pembroke High School Malden Catholic High School Mr. Mike Denise Mr. Craig Najarian, Athletic Director Braintree High School Catholic Memorial High School Dist. D Dr. John Gould, Principal MASS Representative Dighton-Rehoboth's High School Mr. Doug White Mr. Scott Ashworth, Athletic Director MASC Bourne High School Mr. Tass Filledes Dist E. Mr. Gerald O’Connell, Assistant Principal Coaches’ Representative Shrewsbury High School Mr. Frank Carey Mr. Keith Brouillard, Athletic Director Officials’ Representative St. Peter Marian High School Mr. Joseph Cacciatore Mr. Jay Costa, Athletic Director Athletic Director (at Large) Shrewsbury High School Mr. Christopher Bishop Mr. Ben Ivey Mr. William Beando, Principal Wachusett Regional High School MIAA Staff Liaison – Richard Pearson, Associate Director Page 1 of 11 2017 BASEBALL TOURNAMENT ENTRY REQUIREMENTS & INFORMATION DATES TOURNAMENT DIRECTORS Tournament Director contact Season Schedule & Commitment: April 15, 2018 information is available in the "Members Only" section of the MIAA website Tournament Entry: May 24, 2018 Cut-Off Date: 1A – 5:00 PM Mon. May 28, 2018 North Teams under consideration for the 1A Mr. -

Guide to Softball Rules and Basics
Guide to Softball Rules and Basics History Softball was created by George Hancock in Chicago in 1887. The game originated as an indoor variation of baseball and was eventually converted to an outdoor game. The popularity of softball has grown considerably, both at the recreational and competitive levels. In fact, not only is women’s fast pitch softball a popular high school and college sport, it was recognized as an Olympic sport in 1996. Object of the Game To score more runs than the opposing team. The team with the most runs at the end of the game wins. Offense & Defense The primary objective of the offense is to score runs and avoid outs. The primary objective of the defense is to prevent runs and create outs. Offensive strategy A run is scored every time a base runner touches all four bases, in the sequence of 1st, 2nd, 3rd, and home. To score a run, a batter must hit the ball into play and then run to circle the bases, counterclockwise. On offense, each time a player is at-bat, she attempts to get on base via hit or walk. A hit occurs when she hits the ball into the field of play and reaches 1st base before the defense throws the ball to the base, or gets an extra base (2nd, 3rd, or home) before being tagged out. A walk occurs when the pitcher throws four balls. It is rare that a hitter can round all the bases during her own at-bat; therefore, her strategy is often to get “on base” and advance during the next at-bat. -

Suwanee Baseball League Division Baseball Rules Minor
SUWANEE BASEBALL LEAGUE DIVISION BASEBALL RULES MINOR All games will be played in accordance with National Federation of High School (NFHS) rules unless otherwise modified by the following rules. I. GAME TIMES/SCORING A. A game shall consist of no more than 6 innings, or 5 ½ if the home team is ahead. B. Time limit for games shall be 1 hour and 30 minutes. The game is official when the scheduled time has expired, and the current inning is completed. No new inning may start if there are five (5) minutes or less minutes of scheduled time remaining when the last out is recorded in the previous inning. If both teams have the same number of runs at the end of the scheduled time period, with both teams having batted the same number of innings, the game will end in a tie and be recorded as such in the league standings. A new inning is defined as being “the previous inning has concluded”. There is to be no stalling in taking the field or batting. If greater than or equal to 5 minutes is remaining at the conclusion of the home team batting, a new inning will be played. C. If the game is being played at North Gwinnett, the North Gwinnett team will be responsible for preparing the field, keeping the official scorebook and keeping the scoreboard. If the game is being played at Peachtree Ridge, the Peachtree Ridge team will be responsible for preparing the field, keeping the official scorebook and keeping the scoreboard. D. A team may score a maximum of six (6) runs per inning for all innings.