DOCSLIB.ORG

The Arrhenius Equation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Arrhenius Equation CHEM 2880 - Kinetics Determining Rate Order As mentioned earlier, the rate order of a reaction can only be determined experimentally. A number of methods can be used to determine both the reaction order and the rate constant. 1. Integration method - the concentration (of reagent or product) is measured at various time intervals, and the integrated rate law equations are plotted. The order is determined by the plot with the best linear fit (most consistent k value). 2. Isolation method - if more than one reactant is involved, the reaction is run several times, each time changing the initial concentration of one of the reagents. Any corresponding change in the rate is due to the reagent that changed concentration and the corresponding order can be determined. Once the order wrt to each reagent has been determined the overall rate can be calculated. 3. Reagents in excess - this method can be used to reduce the order of a reaction (as mentioned earlier), and make complicated rate laws easier to analyze. 40 CHEM 2880 - Kinetics 4. Differential method - for an nth-order reaction, the rate law is: taking logarithms of both sides yields: Thus a plot of log v vs log[A] will be linear with a slope of n and an intercept of log k. This method often involves measuring the initial rate of reaction at several different initial concentrations. This has the advantages of: avoiding any complications caused by build up of products; and measuring rate at a time when the concentration is known most accurately. From: Physical Chemistry for the Chemical and Biological Sciences, R. Chang, University Science Books, 2000, p. 459. 41 CHEM 2880 - Kinetics Examples: Integration method: The following pharmacokinetic data were determined for the elimination of beta adrenergic blocking agents (beta blockers, used to treat hypertension) from the blood. The drug was administered to the patients and their blood plasma was monitored for the drug over a period of time. Determine the order of reaction and rate constant for this process. t (min) 30 60 120 150 240 360 480 c (ng/ml) 699 622 413 292 152 60 24 From: Physical chemistry for the life sciences, P.W. Atkins, W.H. Freeman and Company, 2005, p. 252. 42 CHEM 2880 - Kinetics Using the integration method requires making plots for each of zero-, 1st-, and 2nd-order. The respective plots are c vs t, ln c vs t and 1/c vs t. The resulting table and plot look like: t c ln c 1/c*100 30 699 6.55 0.143 60 622 6.43 0.161 120 413 6.02 0.242 150 292 5.68 0.342 240 152 5.02 0.658 360 60 4.09 1.667 480 24 3.18 4.167 Note: The 1/c values have been multiplied by 100 so that the ln c and 1/c plots are on the same scale. The ln c vs t is the best linear fit, indicating a 1st-order process. From the slope of the line, the rate constant is determined to be 7.6 x 10-3 s-1. The elimination of drugs from the body is usually a first order process. 43 CHEM 2880 - Kinetics Isolation method: For the acid catalyzed bromination of acetone: The reaction rate was determined for different initial concentrations of the reagents. Determine the rate law and the rate constant. + [CH33COCH ] [Br2] [H ] Rate of dis- appearance of Br2 (M) (M) (M) (M s-1) 1 0.30 0.050 0.050 5.7 x 10-5 2 0.30 0.10 0.050 5.7 x 10-5 3 0.30 0.050 0.10 1.2 x 10-4 4 0.40 0.050 0.20 3.1 x 10-4 5 0.40 0.050 0.050 7.6 x 10-5 From: Physical Chemistry for the Chemical and Biological Sciences, R. Chang, University Science Books, 2000, p. 507. 44 CHEM 2880 - Kinetics For this method, we want to compare the reaction rates between two different runs where the concentration of only one reagent has changed from one run to the next. Comparing runs 1 and 2, the concentrations of [H+] and [CH33COCH ] are constant, the [Br2] increases by a factor of 2, and the rate does not change. Therefore the rate is not dependant on the [Br2] and the reaction is zero-order in [Br2]. Comparing runs 1 and 3, the concentrations of [Br2] and + [CH33COCH ] are constant, the [H ] increases by a factor of 2, and the rate increases by a factor of 2.2. Therefore the rate is directly proportional to the [H+] and the reaction is 1st-order in [H+]. Comparing runs 1 and 5, the concentrations of [H+] and [Br23] are constant, the [CH COCH3] increases by a factor of 1.3, and the rate increases by a factor of 1.3. Therefore the rate is directly proportional to the st [CH33COCH ] and the reaction is 1 -order in [CH33COCH ]. The rate law for this reaction is: + v = k [CH33COCH ][H ] 45 CHEM 2880 - Kinetics Using the rate law, the rate constant for each run can be calculated and the average rate constant determined. + [CH33COCH ] [H ] Rate k (M) (M) (M s-1) (M-1 s)-1 1 0.30 0.050 5.7 x 10-5 3.8 x 10-3 2 0.30 0.050 5.7 x 10-5 3.8 x 10-3 3 0.30 0.10 1.2 x 10-4 4.0 x 10-3 4 0.40 0.20 3.1 x 10-4 3.9 x 10-3 5 0.40 0.050 7.6 x 10-5 3.8 x 10-3 -3 Avg 3.86 x 10 46 CHEM 2880 - Kinetics Differential method: For the binding of glucose to the enzyme hexokinase, the -1 -1 following initial rate (v0) data (in mol L s )were obtained: [glucose] (mmol L-1) 1.00 1.54 3.12 4.02 1.34 5.0 7.6 15.5 20.0 3.00 7.0 11.0 23.0 31.0 10.0 21.0 34.0 70.0 96.0 [Enzyme] (mmol L-1) Determine the rate law and the rate constant. From: Physical chemistry for the life sciences, P.W. Atkins, W.H. Freeman and Company, 2005, p. 248. 47 CHEM 2880 - Kinetics The data provided are initial rate constants for different initial concentrations for the two reagents, glucose and hexokinase. The rate law willbe of the form: ab v00 = k[glucose] [hexokinase]0 For a constant [hexokinase]0, the order of reaction wrt to glucose can be determined using: logv00 = log k’ + alog[glucose] b where k’ = k[hexokinase]0 Plotting log v00 vs log[glucose] for each [hexokinase]0 yields straight lines with slopes of a and intercepts of log k’. log k’ = log k + blog[hexokinase]0 Plotting log k’ vs log[hexokinase]0 yields a straight line with a slope of b and an intercept of log k. 48 CHEM 2880 - Kinetics The table with the data converted to logs looks like: log [glucose] (mmol L-1) log[hexokinase] k’ -3.00 -2.81 -2.51 -2.40 (mmol L-1) 1.34 0.699 0.881 1.19 1.30 -2.87 3.69 3.00 0.845 1.04 1.36 1.49 -2.52 4.04 10.0 1.32 1.53 1.85 1.98 -2.00 4.56 [hexokinase] (mmol L-1) The plot of this data looks like: The three lines all have slopes of 1, so the reaction is 1st order wrt to glucose. The intercepts are tabulated above. 49 CHEM 2880 - Kinetics The plot of log k’ vs log[hexokinase]0 looks like: The slope and intercept are 1 and 6.55 respectively. Therefore b is 1and k is 106.55 = 3.6 x 106. Thus the rate law for this reaction is: v = 3.6 x 106[glucose][hexokinase] 50 CHEM 2880 - Kinetics More Examples: Sucrose (table sugar) undergoes hydrolysis (reaction with water) to produce fructose and glucose: 6 C122HO211 + H2O C61H 26O (fructose) + C61H 26O (glucose) “This reaction has particular significance in the candy industry. First, fructose is sweeter than sucrose. Second, a mixture of fructose and glucose, called invert sugar, does not crystallize, so candy made with this combination is chewier and bot brittle as crystalline sucrose is. Sucrose is dextrorotatory (+) whereas the mixture of glucose and fructose resulting from inversion is levorotatory (-). Thus, a decrease in the concentration of sucrose will be accompanied by a proportional decrease in the optical rotation.” Given the following kinetic data, show that the reaction is first order and find k. t (min) 0 7.20 18.0 27.0 4 optical rotation (") +24.08° +21.40° +17.73° +15.01° -10.73° From: Physical Chemistry for the Chemical and Biological Sciences, R. Chang, University Science Books, 2000, p. 508. 51 CHEM 2880 - Kinetics The total change in optical rotation from t=0 to t=4, is " " ( 0 - 4). This is proportional to the total change in " [sucrose]. The change in optical rotation at time=t, ( 0 - " t) is proportional to the change in [sucrose] at t. thus the [sucrose] remaining at t is: "" " " " " (0 - 4) - ( 0t - ) = t - 4 Since it is a 1st-order reaction: should be linear, and a plot of vs t will have a slope of -k. 52 CHEM 2880 - Kinetics " " " " " t ln(( t- 4)-( 0- 4)) (min) 0.00 +24.08 0.00000 7.20 +21.40 -0.08011 18.0 +17.73 -0.20141 27.0 +15.01 -0.30186 4 -10.73 The plot is linear, so the reaction is 1st-order and k = 1.11 x 10-2 s-1.
Load more

Recommended publications
  • Patnaik-Goldfarb-2016.Pdf
    CONTINUOUS ACTIVATION ENERGY REPRESENTATION OF THE ARRHENIUS EQUATION FOR THE PYROLYSIS OF CELLULOSIC MATERIALS: FEED CORN STOVER AND COCOA SHELL BIOMASS * *,** ABHISHEK S. PATNAIK and JILLIAN L. GOLDFARB *Division of Materials Science and Engineering, Boston University, 15 St. Mary’s St., Brookline, MA 02446 **Department of Mechanical Engineering, Boston University, 110 Cummington Mall, Boston, MA 02215 ✉Corresponding author: Jillian L. Goldfarb, [email protected] Received January 22, 2015 Kinetics of lignocellulosic biomass pyrolysis – a pathway for conversion to renewable fuels/chemicals – is transient; discreet changes in reaction rate occur as biomass composition changes over time. There are regimes where activation energy computed via first order Arrhenius function yields a negative value due to a decreasing mass loss rate; this behavior is often neglected in the literature where analyses focus solely on the positive regimes. To probe this behavior feed corn stover and cocoa shells were pyrolyzed at 10 K/min. The activation energies calculated for regimes with positive apparent activation energy for feed corn stover were between 15.3 to 63.2 kJ/mol and for cocoa shell from 39.9 to 89.4 kJ/mol. The regimes with a positive slope (a “negative” activation energy) correlate with evolved concentration of CH4 and C2H2. Given the endothermic nature of pyrolysis, the process is not spontaneous, but the “negative” activation energies represent a decreased devolatilization rate corresponding to the transport of gases from the sample surface. Keywords: Arrhenius equation, biomass pyrolysis, evolved compounds, activation energy INTRODUCTION Fossil fuels comprise the majority of the total energy supply in the world today.1 One of the most critical areas to shift our dependence from fossil to renewable fuels is in energy for transportation, which accounts for well over half of the oil consumed in the United States.
    [Show full text]
  • Temperature Dependence of Reaction Rates
    Module 6 : Reaction Kinetics and Dynamics Lecture 29 : Temperature Dependence of Reaction Rates Objectives In this Lecture you will learn to do the following Give examples of temperature dependence of reaction rate constants (k). Define the activated complex. Outline Arrhenius theory of temperature dependence of k. Rationalize the temperature dependence of molecular speeds and molecular energies through appropriate distribution functions. Summarize other theories for temperature dependence of k. 29.1 Introduction Temperature dependence of physical and chemical parameters is of great interests to chemists and predicting correct temperature dependence is a test as well as a challenge for framing suitable theories. In thermodynamics, temperature dependence of heat capacities and enthalpies was used in calculating equilibrium constants at different temperatures. The departure of real gas behaviour from the ideal gas behaviour is expressed through the temperature dependent viral coefficients. In chemical kinetics, it was observed that for many reactions, increasing the temperature by 10oC, doubled the rates. In rate processes, the temperature dependence is quite striking. In this lecture, we will consider preliminary attempts at explaining this temperature dependence and take up the detailed explanations in later lectures. A knowledge of the distribution of molecular speeds at a given temperature and the population of energy levels is essential in understanding the temperature dependent rate processes and these aspects will also be outlined here. The most common analysis of temperature dependence of reaction rates over a small temperature range of a few tens of degrees Celsius has been through the Arrhenius equation given below. k = A e - Ea / RT (29.1) Where A is the pre exponential factor (commonly referred to as the frequency factor) and Ea is the energy of activation.
    [Show full text]
  • Activation Energy (Ea)
    Activation Energy (Ea) Ea value indicates that how temp. changes during processing or storage affect the k value of the reaction. The higher Ea value of the reaction, the more sensitive for the reaction to temp. changes during storage or processing. Ea value is specific for each chemical, microbial and enzymatic reaction. 1 √ Ea cannot be directly measured. √ Ea is calculated from Arrhenius equation. This equation (described by Svante Arrhenius in 1889) gives the relationship between k and temp. of processing or storage. Therefore, we need k and temp. values to determine Ea 2 Arrhenious equation –Ea/ RT k = ko e k: Reaction rate constant (for any reaction order) ko: frequency factor (same unit as k) Ea: Activation energy of the reaction (cal/mole of J/mole) R: Gas constant (1.987 cal/(mole K) or 8.314 J/(mole K) T: Temperature (K) 3 Take ln of both sides – Ea 1 ln k = (—— ——) + ln ko R T ↕ ↕ ↕ ↕ y = a x + b Find the equivalence of this equ. on log10 4 To determine Ea value graphically √ First identify the quality factor of concern and then determine k values at least at three different temp., preferably at five different processing or storage temp. √ Then, plot k values vs 1/T values. Using aritmetic graph paper: Take ln of k values and reciprocal of temp. values in Kelvin and then plot ln k vs 1/T. Slope will be equal to –Ea/R. Using semi-log graph paper: Plot original k values vs 1/T values. Slope will be equal to –Ea/2.303R.
    [Show full text]
  • Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems Nathan Mitchell East Tennessee State University
    East Tennessee State University Digital Commons @ East Tennessee State University Electronic Theses and Dissertations Student Works 5-2018 Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems Nathan Mitchell East Tennessee State University Follow this and additional works at: https://dc.etsu.edu/etd Part of the Analytical Chemistry Commons Recommended Citation Mitchell, Nathan, "Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems" (2018). Electronic Theses and Dissertations. Paper 3430. https://dc.etsu.edu/etd/3430 This Thesis - Open Access is brought to you for free and open access by the Student Works at Digital Commons @ East Tennessee State University. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of Digital Commons @ East Tennessee State University. For more information, please contact [email protected]. Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems ________________________ A thesis presented to the faculty of the Department of Chemistry East Tennessee State University In partial fulfillment of the requirements for the degree Master of Science in Chemistry ______________________ by Nathan Mitchell May 2018 _____________________ Dr. Dane Scott, Chair Dr. Greg Bishop Dr. Marina Roginskaya Keywords: Thermodynamic Analysis, Hydrolysis, Linear Solvent Energy Relationships, Cosolvent Systems, Acetonitrile ABSTRACT Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems by Nathan Mitchell Acetic anhydride hydrolysis in water is considered a standard reaction for investigating activation energy parameters using cosolvents. Hydrolysis in water/acetonitrile cosolvent is monitored by measuring pH vs. time at temperatures from 15.0 to 40.0 °C and mole fraction of water from 1 to 0.750.
    [Show full text]
  • Continuous Activation Energy Representation of the Arrhenius Equation for the Pyrolysis of Cellulosic Materials: Feed Corn Stover and Cocoa Shell Biomass
    CELLULOSE CHEMISTRY AND TECHNOLOGY CONTINUOUS ACTIVATION ENERGY REPRESENTATION OF THE ARRHENIUS EQUATION FOR THE PYROLYSIS OF CELLULOSIC MATERIALS: FEED CORN STOVER AND COCOA SHELL BIOMASS * *,** ABHISHEK S. PATNAIK and JILLIAN L. GOLDFARB *Division of Materials Science and Engineering, Boston University, 15 St. Mary’s St., Brookline, MA 02446 ** Department of Mechanical Engineering, Boston University, 110 Cummington Mall, Boston, MA 02215 ✉Corresponding author: Jillian L. Goldfarb, [email protected] Received January 22, 2015 Kinetics of lignocellulosic biomass pyrolysis – a pathway for conversion to renewable fuels/chemicals – is transient; discreet changes in reaction rate occur as biomass composition changes over time. There are regimes where activation energy computed via first order Arrhenius function yields a negative value due to a decreasing mass loss rate; this behavior is often neglected in the literature where analyses focus solely on the positive regimes. To probe this behavior feed corn stover and cocoa shells were pyrolyzed at 10K/min. The activation energies calculated for regimes with positive apparent activation energy for feed corn stover were between 15.3 to 63.2 kJ/mol and for cocoa shell from 39.9to 89.4 kJ/mol. The regimes with a positive slope (a “negative” activation energy) correlate with evolved concentration of CH 4 and C 2H2. Given the endothermic nature of pyrolysis, the process is not spontaneous, but the “negative” activation energies represent a decreased devolatilization rate corresponding to the transport of gases from the sample surface. Keywords : Arrhenius equation, biomass pyrolysis, evolved compounds, activation energy INTRODUCTION Fossil fuels comprise the majority of the total There are multiple methods used to analyze energy supply in the world today.
    [Show full text]
  • Activation Energies and Temperature Dependencies of the Rates of Crystallization and Melting of Polymers
    polymers Review Activation Energies and Temperature Dependencies of the Rates of Crystallization and Melting of Polymers Sergey Vyazovkin Department of Chemistry, University of Alabama at Birmingham, 901 S. 14th Street, Birmingham, AL 35294, USA; [email protected] Received: 20 April 2020; Accepted: 5 May 2020; Published: 7 May 2020 Abstract: The objective of this review paper is to survey the phase transition kinetics with a focus on the temperature dependence of the rates of crystallization and melting, as well as on the activation energies of these processes obtained via the Arrhenius kinetic treatment, including the treatment by isoconversional methods. The literature is analyzed to track the development of the basic models and their underlying concepts. The review presents both theoretical and practical considerations regarding the kinetic analysis of crystallization and melting. Both processes are demonstrated to be kinetically complex, and this is revealed in the form of nonlinear Arrhenius plots and/or the variation of the activation energy with temperature. Principles which aid one to understand and interpret such results are discussed. An emphasis is also put on identifying proper computational methods and experimental data that can lead to meaningful kinetic interpretation. Keywords: activation energy; Arrhenius equation; crystallization; differential scanning calorimetry (DSC); melting; multi-step kinetics 1. Introduction Evidently, it is a fact of nature that the rate of a broad variety of processes responds exponentially to temperature changes. For chemical reactions, this fact is reflected in a number of empirical equations [1], including the one proposed by Arrhenius [2]. Among those, the Arrhenius equation has thrived because it was backed up by the theories of the activated complex and transition state [3,4].
    [Show full text]
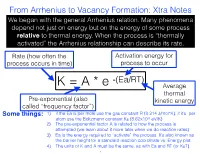
  • From Arrhenius to Vacancy Formation: Xtra Notes We Began with the General Arrhenius Relation
    From Arrhenius to Vacancy Formation: Xtra Notes We began with the general Arrhenius relation. Many phenomena depend not just on energy but on the energy of some process relative to thermal energy. When the process is “thermally activated” the Arrhenius relationship can describe its rate. Rate (how often the Activation energy for process occurs in time) process to occur -(Ea/RT) K = A * e Average thermal Pre-exponential (also kinetic energy called “frequency factor”) Some things: 1) if the Ea is per mole use the gas constant R (8.314 J/mol*K), if it’s per atom use the Boltzmann constant KB (8.62x10-5 eV/K) 2) The pre-exponential factor A is related to how the process is attempted (we learn about it more later when we do reaction rates) 3) Ea is the energy required to “activate” the process. It’s also known as the barrier height for a standard reaction coordinate vs. Energy plot. 4) The units of K and A must be the same, as with Ea and RT (or KBT). 1 From Arrhenius to Vacancy Formation: Xtra Notes K=A*e -(Ea/RT) ln(K)=ln(A)-Ea/RT Take the log of the Arrhenius equation and we get a nice linear relationship between ln(K) and 1/T, like this: Some things: Y-intercept = lnA 1) This is sometimes called an “Arrhenius plot,” showing the inverse relation between reaction rates and temperature 2) The negative slope gives the activation energy, Ea: slope = -Ea/R 3) Extrapolation of the Arrhenius plot slope=-Ea/R back to the y-intercept gives ln(A) ln(k) 4) This plot shows how activation energy and temperature affect the sensitivity of the reaction rate 1/Temperature 2 From Arrhenius to Vacancy Formation: Xtra Notes Next we related a thermally activated process to vacancy formation.
    [Show full text]
  • Arrheniusan Activation Energy of Separation for Different Parameters Regulating the Process
    Physicochem. Probl. Miner. Process., 54(4), 2018, 1152-1158 Physicochemical Problems of Mineral Processing ISSN 1643-1049 http://www.journalssystem.com/ppmp © Wroclaw University of Science and Technology Received May 14, 2018; reviewed; accepted June 21, 2018 Arrheniusan activation energy of separation for different parameters regulating the process Jan Drzymala Wroclaw University of Science and Technology, Faculty of Geoengineering, Mining and Geology, Wybrzeze Wyspianskiego 27, 50-370 Wroclaw, Poland Corresponding author: [email protected] (Jan Drzymala) Abstract: The Arrhenius model, that relates the activation energy with the kinetic constant and process temperature, was applied for flotation as a separation process, and next was extended to other incentive parameters such as the frother concentration, NaCl content and hydrophobicity. It was shown that determination of the activation energy caused by other incentive parameters (i.e. particle size, surface potential) was also possible. The units of the activation energy depend on the type of the separation process and incentive parameter. For contact angle regulating flotation the activation energy unit is mJ/m2, while for the frother concentration is J. It is known that instead in joules, the activation energy can also be expressed in J/mol and in kT or RT units, where k is the Boltzmann constant, R gas constant and T is absolute temperature in kelvins. Even though different formulas of the specific Gibbs potential were used for calculation of activation energy caused by various incentive parameters, there was generally a good agreement between the extend of changes of the first order kinetic constants of the process and activation energy value.
    [Show full text]
  • The Basic Theorem of Temperature-Dependent Processes
    Review The Basic Theorem of Temperature-Dependent Processes Valentin N. Sapunov 1,* , Eugene A. Saveljev 1, Mikhail S. Voronov 1, Markus Valtiner 2,* and Wolfgang Linert 2,* 1 Department of Chemical Technology of Basic Organic and Petrochemical Synthesis, Mendeleev University of Chemical Technology of Russia, Miusskaya sq. 9, 125047 Moscow, Russia; [email protected] (E.A.S.); [email protected] (M.S.V.) 2 Department of Applied Physics, Vienna University of Technology, Wiedner Hauptstrasse 8-10/134-AIP, 1040 Vienna, Austria * Correspondence: [email protected] (V.N.S.); [email protected] (M.V.); [email protected] (W.L.) Abstract: The basic theorem of isokinetic relationships is formulated as “if there exists a linear correlation “structure∼properties” at two temperatures, the point of their intersection will be a common point for the same correlation at other temperatures, until the Arrhenius law is violated”. The theorem is valid in various regions of thermally activated processes, in which only one parameter changes. A detailed examination of the consequences of this theorem showed that it is easy to formulate a number of empirical regularities known as the “kinetic compensation effect”, the well- known formula of the Meyer–Neldel rule, or the so-called concept of “multi-excitation entropy”. In a series of similar processes, we examined the effect of different variable parameters of the process on the free energy of activation, and we discuss possible applications. Keywords: isokinetic relationship; Meyer–Neldel; multi-excitation entropy; free energy of activation Citation: Sapunov, V.N.; Saveljev, E.A.; Voronov, M.S.; Valtiner, M.; Linert, W.
    [Show full text]
  • The Development of the Arrhenius Equation
    The Development of the Arrhenius Equation Keith J. Laidler Onawa-Carleton Institute for Research and Graduate Studies in Chemistry, University of Onawa, Onawa, Ontario. Canada KIN 684 Todav the influence of temperature on the rate of chemical k = AFn (1 +GO) (4) reactions is almost always interpreted in terms of what is now known as the Arrhenius equation. According to this, a rate In terms of the absolute temperature T, the equation can he constant h is the product of a pre- exponentid ("frequency") written as factor A and an exponential term k = A'FT(l + G'T) (5) k = A~-EIRT (1) In 1862 Berthelot (9) presented the equation where R is the gas constant and E is the activation energy. The Ink=A'+DT or k = AeDT (6) apparent activation energy E.,, is now defined (I) in terms of this equation as A ronsi(lrrable niimlwr of workers bupportrd thls equation, which was taken seriously at least until 19011 (101. In 1881 Warder (11, 12) prop,wd thr reli~tlonshlp (a k)(b T) = e Often A and E can he treated as temperature independent. + - (7) For the analvsis of more precise rate-temperature data, par- where a, b, and c are constants, and later Mellor (4) pointed ticularly those covering a wide temperature range, it is usual out that if one multiplies out this formula, expands the factor to allow A to he proportional to T raised to a power m, so that in T and accepts only the first term, the result is the equation hecomes k = a' + b'T2 (8) k = A'T~~~-E/RT (3) Equation (7) received some support from results obtained by where now A' is temperature independent.
    [Show full text]
  • Application of Arrhenius Equation and Plackett-Burman Design to Ascorbic Acid Syrup Development
    Naresuan University Journal 2004; 12(2) : 1-12 1 Application of Arrhenius Equation and Plackett-Burman Design to Ascorbic Acid Syrup Development Srisagul Sungthongjeen Department of Pharmaceutical Technology, Faculty of Pharmaceutical Sciences, Naresuan University, Phitsanulok 65000, Thailand. Corresponding author. E-mail address: [email protected] (S. Sungthongjeen) Received 19 April 2004; accepted 29 June 2004 Abstract Stability testing and drug-excipients compatibility of pharmaceutical dosage forms are necessary to perform during the early stages of product development. The aim of this study was to apply Arrhenius equation and Plackett-Burman design for stability testing and drug-excipients compatibility of formulations, respectively. The stability of ascorbic acid in syrup was examined using an accelerated stability testing according to the Arrhenius equation. The formulations were stored at room temperature and over the temperature range of 40-70°C. A linear regression line was obtained from Arrhenius plot of the reaction rate (k) against reciprocal of degree kelvin. The heat of activation was found to be 17.96 kcal/mole. Plackett-Burman experimental design was used to investigate the compatibility of ascorbic acid with various syrup excipients. It was found that glycerin (5%v/v) exerted a significant stabilizing effect on ascorbic acid, whereas sugar cane syrup (33.3%v/v) had destabilizing effect. The other excipients appeared to be no significant effect on ascorbic acid stability. The study demonstrated that Arrhenius equation would be useful for the prediction of product stability and the stabilizing or destabilizing effects of excipients could be identified by Plackett-Burman design. Keywords: Arrhenius equation, Plackett-Burman design, Ascorbic acid syrup Introduction Stability testing of pharmaceutical dosage forms usually begins during the early stages of product development, the main purpose is to establish a product shelf life.
    [Show full text]
  • Chemical Kinetics (Note -2) the Arrhenius Equation: the Arrhenius
    Chemical Kinetics (Note -2) The Arrhenius Equation: The Arrhenius equation is an expression that provides a relationship between the rate constant (of a chemical reaction), the absolute temperature, and the A factor (also known as the pre- exponential factor). The expression of the Arrhenius equation is: Arrhenius Equation Where, k denotes the rate constant of the reaction A denotes the pre-exponential factor which, in terms of the collision theory, is the frequency of correctly oriented collisions between the reacting species e is the base of the natural logarithm (Euler’s number) Ea denotes the activation energy of the chemical reaction (in terms of energy per mole) R denotes the universal gas constant T denotes the absolute temperature associated with the reaction (in Kelvin) If the activation energy is expressed in terms of energy per reactant molecule, the universal gas constant must be replaced with the Boltzmann constant (kB) in the Arrhenius equation. Arrhenius Plot When logarithms are taken on both sides of the equation, the Arrhenius equation can be written as follows: ln k = ln(Ae-Ea/RT) Solving the equation further: -Ea/RT ln k = ln(A) + ln(e ) ln k = ln(A) + (-Ea/RT) = ln(A) – (Ea/R)(1/T) Since ln(A) is a constant, the equation corresponds to that of a straight line (y = mx + c) whose slope (m) is -Ea/R. When the logarithm of the rate constant (ln K) is plotted on the Y-axis and the inverse of the absolute temperature (1/T) is plotted on the X-axis, the resulting graph is called an Arrhenius plot.
    [Show full text]