DOCSLIB.ORG

Volume 22 Spring 2021 the Journal of Undergraduate Research In

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Volume 22 Spring 2021 the Journal of Undergraduate Research In The Journal of Undergraduate Research Volume 22 in Natural Sciences and Mathematics Spring 2021 The Journal of Undergraduate Research in Natural Sciences and Mathematics Volume 22 | Spring 2021 Marks of a CSUF graduate from the College of Natural Sciences and Mathematics GRADUATES FROM THE COLLEGE OF NATURAL SCIENCES AND MATHEMATICS: • Understand the basic concepts and principles of science and mathematics. • Are experienced in working collectively and collaborating to solve problems. • Communicate both orally and in writing with clarity, precision, and confidence. • Are adept at using computers to do word processing, prepare spreadsheets and graphs, and use presentation software. • Possess skills in information retrieval using library resources and the internet. • Have extensive laboratory, workshop, and field experience where they utilize the scientific method to ask questions, formulate hypotheses, design and conduct experiments, and analyze data. • Appreciate diverse cultures as a result of working side by side with many people in collaborative efforts in the classroom, laboratory, and on research projects. • Have had the opportunity to work individually with faculty members in conducting research and independent projects, often leading to the generation of original data and contributing to the research knowledge base. • Are capable of working with modern equipment, instrumentation, and techniques. 4 DIMENSIONS DIMENSIONS: The Journal of Undergraduate Research in Natural Sciences and Mathematics is an official publication of California State University, Fullerton. DIMENSIONS is published annually by CSUF, 800 N. State College Blvd., Fullerton, CA 92834. Copyright ©2021 CSUF. Except as otherwise provided, DIMENSIONS grants permission for material in this publication to be copied for use by non-profit educational institutions for scholarly or instructional purposes only, provided that 1) copies are distributed at or below cost, 2) the author and DIMENSIONS are identified, and 3) proper notice of copyright appears on each copy. If the author retains the copyright, permission to copy must be obtained directly from the author. About the Cover Mathematics and art have long been intertwined: The ancient Greeks believed that “perfect” mathematical proportions governed what was aesthetically pleasing, and this belief carried over to the Renaissance where artists used precise mathematical measurements to replicate the natural world in man-made creations. This was possible because math and nature are also inherently related: every complex structure and elaborate pattern in nature can usually be broken down into a series of equations and theorems. I sought to illustrate that triangular relation between math, art, and nature in this cover, by highlighting the persistence of the Golden Ratio/Golden Spiral, a mathematical understanding of proportions based on the Fibonacci sequence, in the natural geometry of objects studied in various fields. From the swirl of the celestial bodies in a galaxy to the spiral structures formed by complex molecular interactions, all the sciences have a beauty and art to them in isolation, but nothing truly exists in a vacuum, and the marvels of each field of study are further amplified when we celebrate the way all of STEM is simultaneously diverse and wonderfully interconnected. The cover itself is designed to look like traditional 16th/17th century scientific illustration, which originally accompanied naturalist findings and were used to convey exciting and remarkable research, much like the manuscripts and abstracts that fill these pages. Special Thanks Thank you to the CNSM administrative staff for their support, the faculty for advising students and providing them with valuable research opportunities, and Tatiana Pedroza and Anais Perez for their guidance and oversight. 5 DIMENSIONS Editorial Staff Editor-In-Chief Sonali Vyas - Mathematics Advisor Tatiana Pedroza - Assistant Dean for Student Affairs Layout Editor and Cover Designer Sherif Ibraheem - Layout Editor Shannon Chou - Cover Designer Editors Jessica Sherman - Biological Science Mayra Silva - Biological Science Melissa Fernandez - Biological Science Krisha Marie Uy - Biological Science Mykayla Miller- Chemistry and Biochemistry Maria Valdovinos- Geological Sciences Luis Gonzalez - Mathematics Madeline Ceccia - Mathematics Erick Engelby- Physics Anny Antunovich - Physics College of Natural Sciences & Mathematics Dr. Marie Johnson - Dean Dr. Sean E. Walker - Associate Dean Dr. Merri Lynn Casem - Chair, Department of Biological Science Dr. Peter de Lijser - Chair, Department of Chemistry and Biochemistry Dr. Adam Woods - Chair, Department of Geological Sciences Dr. Alfonso Agnew - Chair, Department of Mathematics Dr. Ionel Tifrea - Chair, Department of Physics 6 Dear Titan NSMers, Even in a pandemic, the college and our students still pursued research, designed experiments, collected data, wrote draft upon draft, and ultimately published their findings to share with other mathematicians and scientists. We could not be prouder of the effort that these pages represent, both for the students themselves and for the faculty mentors who stand behind these students and enable this work. On behalf of all of us here in NSM, please enjoy this issue of Dimensions as we celebrate the discovery of new knowledge and the original research of our students. Marie Johnson Dean, College of Natural Sciences and Mathematics 7 Table of Contents 10 Biological Science 52 Geological Sciences 11 Diet of Coyotes in Rural Agricultural Areas of 53 Examining the Concentric Pattern of the Box California: A Comparative Analysis of Stable Isotope Springs pluton, Riverside, California and Stomach Contents Analysis - Author: Alex Valenzuela - Author: Jesi Nonora - Advisor: Vali Memeti, Ph.D. - Advisor: Paul Stapp, Ph.D. 54 An Examination of the Structural and Petrologic 13 Green Waste Perceptions at California State Evolution of the Box Springs Plutonic Complex, University, Fullerton Riverside, CA - Author: Elijah Slaven - Author: Andrew Culleton - Advisor: Joel Abraham, Ph.D. - Advisor: Vali Memeti, Ph.D. 14 Analyzing the Effect of Experimental Evolution on the Host Microbiome in Drosophila melanogaster 55 Lidar analysis of the high-slip section of the Hector - Author: Leah Spalding Mine Earthquake Surface Rupture - Advisor: Parvin Shahrestani, Ph.D. - Author: Brandon Cugini - Advisor: Sinan Akçiz, Ph.D. 15 Chloroplast genomes in the parasitic sandalwood order 67 Testing The Efficacy Of 3D-Printed Geologic Block - Author: Tuesday Weaver Models As Tools For Fostering Spatial Visualization - Advisor: Joshua Der, Ph.D. Abilities - Authors: Joseph Gutierrez, Sinan Akçiz, Natalie 16 Chemistry and Biochemistry Bursztyn, and Kevin Nichols 17 Synthesis and Study of the Pyrochlore La3Sb3Co2O14 for Use as an Oxygen Transport Membrane 70 Geochemistry of basalts and trachyandesites in - Authors: Gonzalez Jimenez and Mark Abad northern Owens Valley, Inyo County, California - Advisor: Allyson Fry-Petit, Ph.D. - Authors: Matthew Pilker, Jeffrey Knott, Fred Phillips, Jade Star Lackey and Angela Jayko 18 New Approaches for the Treatment of Alzheimer’s Disease: Green Chemistry Synthesis and Molecular 71 Mathematics Modeling Studies of Donepezil-Based Analogs 72 Mancala: Divide And Tied - Author: Stephanie Mariel Salvador - Authors: Salma Albakri and Chloe Rhee - Advisor: Stevan Pecic, Ph.D. - Advisor: Alison S. Marzocchi, Ph.D. 28 Human Soluble Epoxide Hydrolase Enzyme- Molecular Modeling Studies and Docking 80 Solvability of Peg Solitaire on Different Graphs Experiments - Author: Gustavo Alonso - Author: Aleksei Solomatov - Advisor: Roberto Soto - Advisor: Stevan Pecic, Ph.D. 81 Statistical Modeling for Discovery: How Movements Within 39 Purification and characterization of a small copper Counties Affect the Spread of the COVID-19 Pandemic carrier in blood fluid - Authors: Gwendolyn Lind, Caleb Peña, and - Authors: Theodore Roque and Heather Carrillo Seth Arreola - Advisor: Maria Linder, Ph.D. - Advisor: Sam Behseta, Ph.D. 8 94 Riemann Sums: Approximating Integrals With 163 Examining Student Understanding of Matrix Semi-Ellipses Algebra and Eigentheory - Authors: Holly C. Anderson, Christine N. Gamez, - Author: Pachi Her and Summer K. Andrews - Advisor: Michael E. Loverude, Ph.D. - Advisor: Alison S. Marzocchi, Ph.D. 168 Mass Distribution Comparison for GW190425 103 Applying Machine Learning Methods in Solid - Author: Marc Daniell Penuliar State Chemistry: Classification and Prediction of - Advisor: Jocelyn Read, Ph.D. Perovskites - Authors: Maria D. Diaz, Brandon Tomich, and 169 Optical scattering measurements for common off Juan Cabrera the shelf highly reflective 1064 nm mirrors - Advisor: Allyson Fry-Petit, Ph.D. and Sam - Authors: Daniel Martinez, Amy Gleckl, Gabriela Behseta, Ph.D. Jaimes, Jazlyn Guerrero, Elenna Capote, Erick Engelby, and Joshua Smith 113 Fibonacci Gaps - Author: Madeline Ceccia 180 Calculating apparent-horizon quantities with - Advisor: Martin Bonsangue, Ph.D. SpECTRE, a next-generation numerical relativity code 123 Minimal Generating Sets of the Monoid of Partial - Author: Marlo Morales Order-preserving Injections - Advisor: Geoffrey Lovelace, Ph.D. - Author: Saul Lopez - Advisor: Scott Annin, Ph.D. 181 Authors & Editors 135 On Applications of The AM-GM Inequality - Author: Sushanth S. Kumar - Advisor: Bogdan Suceava 142 An Interesting Series and The Geometric Mean of the Numbers in a Positive Interval - Author: Sushanth S. Kumar - Advisor: Bogdan Suceava 147 Maxwell’s
Load more

Recommended publications
  • (ITEP) Application for Admission in 2020
    Integrated Teacher Education Program (ITEP) Application For Admission in 2020 Name: Last First Middle Former Address: Number and Street City Zip Code Telephone: Cell Home Email: Date of Birth: Semester you expect to complete Associate’s degree: Semester that you expect to start at CSUF: Accepted Early Childhood Special CSUF Applied, no response yet Credential Education (ECSE) application Applied, waitlisted Sought: Mild/Moderate status: Not yet applied Moderate/Severe Please indicate your completion status for the following classes (see equivalents on next page): Equivalents to Required Your Equivalent CSUF Classes Community College Course Status CAS 101: Intro to Child Completed Development (required for In Progress all applicants) Not Yet Enrolled CAS 201: Child Family Completed Community (required for In Progress all applicants) Not Yet Enrolled SPED 371: Exceptional Completed Individual (required for all In Progress applicants) Not Yet Enrolled CAS 250: Intro to EC Completed Curriculum (required for In Progress ECSE) Not Yet Enrolled CAS 306: Health, Safety, & Completed Nutrition (required for In Progress ECSE) Not Yet Enrolled MATH 303A: Math for Completed Elementary (required for In Progress Mild/Mod & Mod/Severe) Not Yet Enrolled ENGL 341: Children’s Completed Literature (required for In Progress Mild/Mod & Mod/Severe) Not Yet Enrolled Completed GE Certification In Progress Not Yet Enrolled Please attach an unofficial transcript from all community colleges and/or universities that you have attended. Submit materials to EC 503 at CSUF or [email protected] Integrated Teacher Education Program (ITEP) Application For Admission in 2020 Credential Early Childhood (ECSE) Mild/Moderate Moderate/Severe Core Classes: Core Classes: Core Classes: 1.
    [Show full text]
  • A Statistical Study Nicholas Lambrianou 13' Dr. Nicko
    Examining if High-Team Payroll Leads to High-Team Performance in Baseball: A Statistical Study Nicholas Lambrianou 13' B.S. In Mathematics with Minors in English and Economics Dr. Nickolas Kintos Thesis Advisor Thesis submitted to: Honors Program of Saint Peter's University April 2013 Lambrianou 2 Table of Contents Chapter 1: The Study and its Questions 3 An Introduction to the project, its questions, and a breakdown of the chapters that follow Chapter 2: The Baseball Statistics 5 An explanation of the baseball statistics used for the study, including what the statistics measure, how they measure what they do, and their strengths and weaknesses Chapter 3: Statistical Methods and Procedures 16 An introduction to the statistical methods applied to each statistic and an explanation of what the possible results would mean Chapter 4: Results and the Tampa Bay Rays 22 The results of the study, what they mean against the possibilities and other results, and a short analysis of a team that stood out in the study Chapter 5: The Continuing Conclusion 39 A continuation of the results, followed by ideas for future study that continue to project or stem from it for future baseball analysis Appendix 41 References 42 Lambrianou 3 Chapter 1: The Study and its Questions Does high payroll necessarily mean higher performance for all baseball statistics? Major League Baseball (MLB) is a league of different teams in different cities all across the United States, and those locations strongly influence the market of the team and thus the payroll. Year after year, a certain amount of teams, including the usual ones in big markets, choose to spend a great amount on payroll in hopes of improving their team and its player value output, but at times the statistics produced by these teams may not match the difference in payroll with other teams.
    [Show full text]
  • Dr. John Hernandez Accepts Position of Irvine Valley College President
    CONTACT: Letitia Clark, MPP - 949.582.4920 - [email protected] FOR IMMEDIATE RELEASE: May 28, 2020 Dr. John Hernandez Accepts Position of Irvine Valley College President MISSION VIEJO, CA— A nationwide search, candidate interviews, and public forums were held via Zoom in the selection process to identify the next Irvine Valley College President. After a several month process, a decision has been made, and Chancellor Kathleen Burke has announced that she is recommending that Dr. John Hernandez serve in the role as Irvine Valley College’s new president. Dr. Hernandez has been an educator for over 30 years – 22 of those years in administration. He was appointed President of Santiago Canyon College (Orange, CA) in July 2017 and served as Interim President there from July 2016 until his permanent appointment. Prior to that, he was the college’s Vice President for Student Services (2005 to July 2016). Before joining Santiago Canyon College, Dr. Hernandez was Associate Vice President and Dean of Students at Cal Poly Pomona; Associate Dean for Student Development at Santa Ana College and Assistant Dean for Student Affairs at California State University, Fullerton. Additionally, Dr. Hernandez has been an adjunct instructor in the Student Development in the Higher Education graduate program at California State University, Long Beach and taught counseling and student development courses at various colleges as well. Dr. Hernandez will immediately begin the transition process from his role as President of Santiago Canyon College within the Rancho Santiago Community College District. He is expected to start at Irvine Valley College on August 1, 2020, pending ratification of his contract by the South Orange County Community College District (SOCCCD) Board of Trustees.
    [Show full text]
  • Psychometric G: Definition and Substantiation
    Psychometric g: Definition and Substantiation Arthur R. Jensen University of Culifornia, Berkeley The construct known as psychometric g is arguably the most important construct in all of psychology largelybecause of its ubiquitous presence in all tests of mental ability and its wide-ranging predictive validity for a great many socially significant variables, including scholastic performance and intellectual attainments, occupational status, job performance, in- come, law abidingness, and welfare dependency. Even such nonintellec- tual variables as myopia, general health, and longevity, as well as many other physical traits, are positively related to g. Of course, the causal con- nections in the whole nexus of the many diverse phenomena involving the g factor is highly complex. Indeed, g and its ramifications cut across the behavioral sciences-brainphysiology, psychology, sociology-perhaps more than any other scientific construct. THE DOMAIN OF g THEORY It is important to keep in mind the distinction between intelligence and g, as these terms are used here. The psychology of intelligence could, at least in theory, be based on the study of one person,just as Ebbinghaus discov- ered some of the laws of learning and memory in experimentswith N = 1, using himself as his experimental subject. Intelligence is an open-ended category for all those mental processes we view as cognitive, such as stimu- lus apprehension, perception, attention, discrimination, generalization, 39 40 JENSEN learning and learning-set acquisition, short-term and long-term memory, inference, thinking, relation eduction, inductive and deductive reasoning, insight, problem solving, and language. The g factor is something else. It could never have been discovered with N = 1, because it reflects individual di,fferences in performance on tests or tasks that involve anyone or moreof the kinds of processes just referred to as intelligence.
    [Show full text]
  • Rancho Santiago Community College District Sustainability Plan
    Rancho Santiago Community College District Sustainability Plan Produced by February 2015 ACKNOWLEDGMENTS Trustees Claudia C. Alvarez Arianna P. Barrios John R. Hanna Lawrence R. “Larry” Labrado Jose Solorio Nelida Mendoza Yanez Phillip E. Yarbrough Alana V. Voechting, Student Trustee Chancellor Raúl Rodríguez, Ph.D. Presidents Erlinda Martinez, Ed.D., – Santa Ana College John Weispfenning, Ph.D., – Santiago Canyon College Sustainable RSCCD Committee Members Delmis Alvarado, Classified Staff Kelsey Bain, Classified Staff Michael Collins, Ed.D., Vice President – Santa Ana College Douglas Deaver, Ph.D., Associate Professor Philosophy Leah Freidenrich, Professor Library & Information Science Peter Hardash, Vice Chancellor – Business Operations & Fiscal Services Judy Iannaccone, Director – Public Affairs & Publications Steve Kawa, Vice President – Santiago Canyon College James Kennedy, Vice President – Centennial Education Center Laurene Lugo, Classified Staff Carri Matsumoto, Assistant Vice Chancellor – Facilities Lisa McKowan-Bourguignon, Asst. Professor Mathematics Kimo Morris, Ph.D., Asst. Professor Biology Kyle Murphy, Student Representative – Santa Ana College Elisabeth Pechs – Orange County SBDC Jose Vargas, Vice President – Orange Education Center Nathan Sunderwood, Student Representative – Santiago Canyon College Other Contributors Matt Sullivan, Consultant – Newcomb Anderson McCormick Danielle Moultak, Project Manager – Newcomb Anderson McCormick Sustainability Plan i TABLE OF CONTENTS SECTION 1. EXECUTIVE
    [Show full text]
  • 2020-2021 SCC-OEC Catalog
    215 Catalog 2020-2021 216 SCC Catalog 2020-2021 SANTIAGO CANYON COLLEGE—CONTINUING EDUCATION INSTRUCTIONAL CALENDAR CONTINUING EDUCATION DIVISION JUNE 2020 JANUARY 2021 INSTRUCTIONAL CALENDAR 2020-2021 S M T W T F S S M T W T F S 1 2 3 4 5 6 1 2 FALL SEMESTER 2020 7 8 9 10 11 12 13 3 4 5 6 7 8 9 August 17–21 Faculty projects 14 15 16 17 18 19 20 10 11 12 13 14 15 16 21 22 23 24 25 26 27 17 18 19 20 21 22 23 August 24 INSTRUCTION BEGINS 28 29 30 24 25 26 27 28 29 30 September 7 Labor Day — Holiday 31 November 11 Veterans’ Day — Holiday JULY 2020 FEBRUARY 2021 November 23–28 Thanksgiving recess S M T W T F S S M T W T F S December 18 INSTRUCTION ENDS 1 2 3 4 1 2 3 4 5 6 December 21–January 8 Winter recess 5 6 7 8 9 10 11 7 8 9 10 11 12 13 12 13 14 15 16 17 18 14 15 16 17 18 19 20 SPRING SEMESTER 2021 19 20 21 22 23 24 25 21 22 23 24 25 26 27 January 8, 11, 12 Faculty projects 26 27 28 29 30 31 28 January 13 INSTRUCTION BEGINS January 18 Martin Luther King, Jr. — Holiday AUGUST 2020 MARCH 2021 February 12 Lincoln’s Birthday (Observed) S M T W T F S S M T W T F S February 15 President’s Day — Holiday 1 1 2 3 4 5 6 March 29–April 3 OSpring recess* 2 3 4 5 6 7 8 7 8 9 10 11 12 13 14 15 16 17 18 19 20 May 27 OEC Commencement 9 10 11 12 13 14 15 16 17 18 19 20 21 22 21 22 23 24 25 26 27 May 27 INSTRUCTION ENDS 23 24 25 26 27 28 29 28 29 30 31 May 231 Memorial Day — Holiday 30 31 SUMMER SESSION 2021 APRIL 2021 June 1 INSTRUCTION BEGINS** SEPTEMBER 2020 S M T W T F S July 4 Independence Day — Holiday Observed July 5 S M T W T F S 1 2 3 August 7 INSTRUCTION ENDS** 1 2 3 4 5 4 5 6 7 8 9 10 6 7 8 9 10 11 12 11 12 13 14 15 16 17 13 14 15 16 17 18 19 18 19 20 21 22 23 24 * OEC Spring recess dates may be adjusted to correspond to unified school district instructional calendar.
    [Show full text]
  • Scc Curriculum & Instruction
    Fall 2020 September 21, 2020 SCC CURRICULUM & INSTRUCTION COUNCIL SCC B-104 1:30 p.m. Meeting Minutes Committee Members Present: L. Aguilera, J. Armstrong, E. Arteaga, D. Bailey, L. Camarco, S. Deeley, C. Evett, L. Fasbinder, A. Freese, A. Garcia, C. Gascon, S. Graham, E. Gutierrez, S. James, J. Kubicka-Miller, R. Lamourelle, C. Malone, S. McLean, R. Miller, M. Newman (Student Representative), N. Pecenkovic, S. Sanchez, N. Shekarabi, J. Shields, M. Stringer, R. Van Dyke-Kao, A. Voelcker, L. Wright Absent: T. Garbis, L. Martin Guests: J. Dennis, L. Espinosa, R. Felipe, M. Laney, N. Parent, B. Sos C. Evett called the meeting to order at 1:30 p.m. I. Approval of Minutes The Minutes for August 31, 2020 were approved. Mover: S. Sanchez Seconder: R. Miller Ayes: L. Aguilera, L. Camarco, S. Deeley, C. Evett, A. Freese, S. Graham, E. Gutierrez, S. James, J. Kubicka-Miller, R. Lamourelle, C. Malone, S. McLean, R. Miller, M. Newman (Student Representative), N. Pecenkovic, S. Sanchez, N. Shekarabi, J. Shields, M. Stringer, R. Van Dyke-Kao, L. Wright Nays: None Abstentions: None Santiago Canyon College 1 What happens here matters. Fall 2020 September 21, 2020 II. Announcements a. Class Capacity C. Evett presented information on Class Capacity. The Curriculum Office updates the class capacity field in Colleague when a request is made. Collegial consultation should take place before the class capacity field is changed. The interim process for the Curriculum Office will be to request that the Dean and CIC Chair be copied when an update to the class capacity field in Colleague is requested.
    [Show full text]
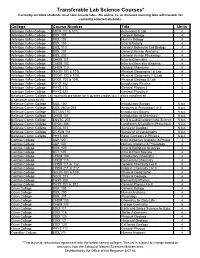
  • Transferable Lab Science Courses* Currently Enrolled Students Must Take On-Site Labs
    Transferable Lab Science Courses* Currently enrolled students must take on-site labs. No online, tv, or distance learning labs will transfer for currently enrolled students. College Course Number Title Units Antelope Valley College ASTR 101 & 101L Astronomy & Lab 4 Antelope Valley College BIOL 101 General Biology 4 Antelope Valley College BIOL 102 Human Biology 4 Antelope Valley College BIOL 103 Intro to Botany 4 Antelope Valley College BIOL 110 General Molecular Cell Biology 4 Antelope Valley College BIOL 201 General Human Anatomy 4 Antelope Valley College BIOL 202 General Human Physiology 4 Antelope Valley College CHEM 101 Intro to Chemistry 5 Antelope Valley College CHEM 102 Intro to Chemistry (Organis) 4 Antelope Valley College CHEM 110 General Chemistry 5 Antelope Valley College GEOG 101 & 101L Physical Geography I & Lab 4 Antelope Valley College GEOG 102 & 102L Physical Geography II & Lab 4 Antelope Valley College GEOL 101 & 101L Physical Geology & Lab 4 Antelope Valley College PHYS 102 Introductory Physics 4 Antelope Valley College PHYS 110 General Physics I 5 Antelope Valley College PHYS 120 General Physics II 5 Bellevue Comm College: Lab sciences are taken for 6 quarter credits (q.c.) which transfers as 4 semester units to VU Bellevue Comm College BIOL 100 Introductory Biology 6 q.c. Bellevue Comm College BIOL 260 or 261 Anatomy & Physiology I or II 6 q.c. Bellevue Comm College BOTAN 110 Introductory Botany 6 q.c. Bellevue Comm College CHEM 101 Introduction to Chemistry 6 q.c. Bellevue Comm College ENVSC 207 Field & Lab Environmental Science 6 q.c. Bellevue Comm College GEOG 206 Landforms & Landform Processes 6 q.c.
    [Show full text]
  • {Download PDF} the Sabermetric Revolution Assessing the Growth of Analytics in Baseball 1St Edition Ebook, Epub
    THE SABERMETRIC REVOLUTION ASSESSING THE GROWTH OF ANALYTICS IN BASEBALL 1ST EDITION PDF, EPUB, EBOOK Benjamin Baumer | 9780812223392 | | | | | The Sabermetric Revolution Assessing the Growth of Analytics in Baseball 1st edition PDF Book Citations should be used as a guideline and should be double checked for accuracy. The Milwaukee Brewers have made a sabermetric shift under GM David Stearns, who took over in the fall of , and the new front office team of the Minnesota Twins also has sabermetric tendencies. The Sabermetric Revolution sets the record straight on the role of analytics in baseball. However, over the past two decades, a wider range of statistics made their way into barroom debates, online discussion groups, and baseball front offices. This is a very useful book. Subscribe to our Free Newsletter. But, be on guard, stats freaks: it isn't doctrinaire. He is the Robert A. Frederick E. Rocketed to popularity by the bestseller Moneyball and the film of the same name, the use of sabermetrics to analyze player performance has appeared to be a David to the Goliath of systemically advantaged richer teams that could be toppled only by creative statistical analysis. Also in This Series. Prospector largest collection. But how accurately can crunching numbers quantify a player's ability? Goodreads helps you keep track of books you want to read. The book is ideal for a reader who wishes to tie together the importance of everything they have digested from sites like Fangraphs , Baseball Prospectus , Hardball Times , Beyond the Box Score , and, even, yes, Camden Depot. Ryne rated it liked it May 27, Not because I rejected new age stats, but because I never sought them out.
    [Show full text]
  • Does a Fitness Factor Contribute to the Association Between Intelligence
    ARTICLE IN PRESS INTELL-00516; No of Pages 11 Intelligence xxx (2009) xxx–xxx Contents lists available at ScienceDirect Intelligence journal homepage: Does a fitness factor contribute to the association between intelligence and health outcomes? Evidence from medical abnormality counts among 3654 US Veterans Rosalind Arden a,⁎, Linda S. Gottfredson b, Geoffrey Miller c a Social, Genetic, Developmental and Psychiatry Centre, Institute of Psychiatry, King's College London, London SE5 8AF, United Kingdom b School of Education, University of Delaware, Newark, DE 19716, USA c Psychology Department, Logan Hall 160, University of New Mexico, MSC03 2220 Albuquerque, NM 87131-1161, USA article info abstract Available online xxxx We suggest that an over-arching ‘fitness factor’ (an index of general genetic quality that predicts survival and reproductive success) partially explains the observed associations between health Keywords: outcomes and intelligence. As a proof of concept, we tested this idea in a sample of 3654 US Fitness Vietnam veterans aged 31–49 who completed five cognitive tests (from which we extracted a g Intelligence factor), a detailed medical examination, and self-reports concerning lifestyle health risks (such Cognitive epidemiology as smoking and drinking). As indices of physical health, we aggregated ‘abnormality counts’ of Health physician-assessed neurological, morphological, and physiological abnormalities in eight Mutation load categories: cranial nerves, motor nerves, peripheral sensory nerves, reflexes, head, body, skin condition, and urine tests. Since each abnormality was rare, the abnormality counts showed highly skewed, Poisson-like distributions. The correlation matrix amongst these eight abnormality counts formed only a weak positive manifold and thus yielded only a weak common factor.
    [Show full text]
  • UC Merced Proceedings of the Annual Meeting of the Cognitive Science Society
    UC Merced Proceedings of the Annual Meeting of the Cognitive Science Society Title Dynamical cognitive models and the study of individual differences. Permalink https://escholarship.org/uc/item/4sn2v2j0 Journal Proceedings of the Annual Meeting of the Cognitive Science Society, 31(31) ISSN 1069-7977 Authors Kan, Kees Jan Van Der Maas, Han L.J. Publication Date 2009 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Dynamical cognitive models and the study of individual differences Han van der Maas & Kees Jan Kan A large part of psychology concerns the study of individual differences. Why do people differ in personality? What is the structure of individual differences in intelligence? What are the roles of nurture and nature? Researchers in these fields collect data of many subjects and apply statistical methods, most notably latent structure modeling, to uncover the structure and to infer the underlying sources of the individual differences. Cognitive science usually does not concern individual differences. In cognitive models we focus on the general mechanisms of cognitive processes and not the individual properties. We believe that these two traditions of modeling cannot remain separated. Models of mechanisms necessarily precede models of individual differences. We argue against the use of latent structure models of individual differences in psychological processes that do not explicate the underlying mechanisms. Our main example is general intelligence, a concept based on the analysis of group data. Scores on cognitive tasks used in intelligence tests correlate positively with each other, i.e., they display a positive manifold of correlations. The positive manifold is arguably both the best established, and the most striking phenomenon in the psychological study of intelligence.
    [Show full text]
  • Apply for a $500 SCHEC Need Help with Expenses After You Transfer?
    Need help with expenses after you The South Coast Higher Education Council (SCHEC) is pleased to be offering several $500 scholarships for the 2017-2018 academic year. Transfer? Those who meet the following criteria are invited to . apply for a SCHEC Scholarship: Currently enrolled in a SCHEC institution and will be transferring as a full-time student to a SCHEC four-year college/university* Apply during the 2017-2018 academic year for a Have a 3.0 or higher cumulative GPA Applications must be postmarked no later than $500 March 10, 2017! SCHEC Application materials can be found at: http://www.schec.net Questions? Contact: Scholarship Melissa Sinclair at CSU Fullerton: [email protected] Carmen Di Padova at Alliant International University: [email protected] Alliant International University CSU Long Beach Rio Hondo College The following colleges, Argosy University Cypress College Saddleback College universities and Azusa Pacific University DeVry University Santa Ana College Biola University El Camino College Santiago Canyon College professional schools Brandman University Fullerton College Southern California University are members of the Cerritos College Golden West College Trident University International South Coast Higher Chapman University Hope International University Trinity Law School Citrus College Irvine Valley College UC, Irvine Education Council Coastline College Loma Linda University UC, Riverside (SCHEC): Concordia University Long Beach City College University of La Verne Columbia University Mt. San Antonio College University of Redlands CSPU, Pomona National University Vanguard University CSU, Dominguez Hills Orange Coast College Webster University CSU, Fullerton Pepperdine University—Irvine Whittier College .
    [Show full text]