DOCSLIB.ORG

Solving Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Solving Equations CHAPTER Solving Equations How far can an BEFORE athlete run in In the previous chapter you’ve . • Performed operations with integers 10 seconds? • Written and evaluated variable expressions Now In Chapter 2 you’ll study . • Using addition, multiplication, and distributive properties • Simplifying variable expressions • Solving equations using mental math • Solving equations using addition, subtraction, multiplication, or division • Solving equations with decimals WHY? So you can solve real-world problems about . • dinosaurs, p. 67 • giant pumpkins, p. 76 • fitness, p. 81 • aviation, p. 89 • mountain climbing, p. 94 • computers, p. 100 • baseball, p. 106 60 PAFL_229843_C02_CO.indd 60 12/17/08 10:58:48 AM Chapter 2 Resources Go to thinkcentral.com • Online Edition • eWorkbook • @HomeTutor • State Test Practice • More Examples • Video Tutor .BUI MATH In the Real World Track Race The world’s fastest athletes can run 100 meters in under 10 seconds. In this chapter, you will use equations to solve problems like finding the average rate at which an athlete runs a race. What do you think? Suppose an athlete runs at an average rate of 10.5 meters per second for 10 seconds. Use the formula distance ϭ rate ϫ time to find the distance the athlete runs. PAFL_229843_C02_CO.indd 61 12/17/08 10:58:54 AM CHAPTER Chapter Prerequisite Skills PREREQUISITE SKILLS QUIZ Review Vocabulary Preparing for Success To prepare for success in this chapter, test your numerical expression, p. 5 knowledge of these concepts and skills. You may want to look at the variable expression, p. 5 pages referred to in blue for additional review. order of operations, p. 16 absolute value, p. 23 1. Vocabulary Describe the difference between a numerical expression decimal, p. 746 and a variable expression. Perform the indicated operation. (pp. 750–752) 2. 3.8 ϩ 7.1 3. 8.23 Ϫ 4.97 4. 5.5 ϫ 9.4 5. 6.93 Ϭ 2.1 Write a variable expression to represent the phrase. (p. 5) 6. 7 more than a number 7. The quotient of a number and 4 Perform the indicated operation. (pp. 29, 34, 42) 8. Ϫ19 ϩ 12 9. 8 Ϫ (Ϫ20) 10. 6(Ϫ7) 11. Ϫ75 Ϭ (Ϫ5) NOTETAKING STRATEGIES USING DEFINITION MAPS When you study a new concept, you Note Worthy can use a definition map to define the concept, describe the concept’s attributes, and give specific examples. A definition You will find a notetaking map for power is shown below. strategy at the beginning of each chapter. Look for additional notetaking and What is it? What are its attributes? study strategies throughout A power is a product A power consists of a base the chapter. of repeated factors: and an exponent. 23 ϭ 2 p 2 p 2. The base is the number POWER that is used as a factor. The base for 23 is 2. What are examples? The exponent is how many 3 6 4 times the base repeats. 2 (0.5) n The exponent for 23 is 3. A definition map will be helpful in Lesson 2.3. 62 PANL_9780547587776_C02_SG.indd 62 11/4/10 6:28:25 PM 2 1 Properties and Operations LESSON . BEFORE Now WHY? You found sums and You’ll use properties of So you can compare the lengths Vocabulary products of numbers. addition and multiplication. of two fish, as in Ex. 48. additive identity, p. 64 multiplicative identity, p. 64 In English, commute means to change locations, and associate means to group together. These words have similar meanings in mathematics. Commutative properties let you change the positions of numbers in a sum or product. Associative properties let you group numbers in a sum or product together. Commutative and Associative Properties Commutative Property of Addition Commutative Property of Multiplication Words In a sum, you can add the Words In a product, you can multiply numbers in any order. the numbers in any order. Numbers 4 ϩ (Ϫ7) ϭ Ϫ7 ϩ 4 Numbers 8(Ϫ5) ϭ Ϫ5(8) Algebra a ϩ b ϭ b ϩ a Algebra ab ϭ ba Associative Property of Addition Associative Property of Multiplication Words Changing the grouping of Words Changing the grouping of the numbers in a sum does not the numbers in a product does change the sum. not change the product. Numbers (9 ϩ 6) ϩ 2 ϭ 9 ϩ (6 ϩ 2) Numbers (3 p 10) p 4 ϭ 3 p (10 p 4) Algebra (a ϩ b) ϩ c ϭ a ϩ (b ϩ c) Algebra (ab)c ϭ a(bc) Example 1 Using Properties of Addition Music You buy a portable CD player for $48, rechargeable batteries with charger for $25, and a CD case for $12. Find the total cost. Solution The total cost is the sum of the three prices. Use properties of addition to group together prices that are easy to add mentally. 48 ϩ 25 ϩ 12 ϭ (48 ϩ 25) ϩ 12 Use order of operations. ϭ (25 ϩ 48) ϩ 12 Commutative property of addition ϭ 25 ϩ (48 ϩ 12) Associative property of addition ϭ 25 ϩ 60 Add 48 and 12. ϭ 85 Add 25 and 60. Answer The total cost is $85. Video Tutor Go to thinkcentral.com Lesson 2.1 Properties and Operations 63 PAFL_229843_C0201.indd 63 12/17/08 12:22:30 PM Example 2 Using Properties of Multiplication .25 ؍ ؊7 and y ؍ Study Strategy Evaluate 4xy when x .4xy ϭ 4(؊7)(25) Substitute ؊7 for x and 25 for y Another Way You can also evaluate the expression [4(Ϫ7)](25) Use order of operations. Ϫ 4( 7)(25) in Example 2 [Ϫ7(4)](25) Commutative property of multiplication simply by multiplying from left to right: Ϫ7[(4)(25)] Associative property of multiplication 4(Ϫ7)(25) ϭ Ϫ28(25) Ϫ7(100) Multiply 4 and 25. .ϭ Ϫ700 Ϫ700 Multiply ؊7 and 100 However, this calculation is more difficult to do mentally. Checkpoint In Exercises 1–3, evaluate the expression. Justify each of your steps. 1. (17 ϩ 36) ϩ 13 2. 8(Ϫ3)(5) 3. 3.4 ϩ 9.7 ϩ 7.6 4. Evaluate 5 x2 y when x ϭ Ϫ6 and y ϭ 20. Example 3 Using Properties to Simplify Variable Expressions Simplify the expression. a. x ϩ 3 ϩ 6 ϭ (x ϩ 3) ϩ 6 Use order of operations. ϭ x ϩ (3 ϩ 6) Associative property of addition ϭ x ϩ 9 Add 3 and 6. b. 4(8y) ϭ (4 p 8)y Associative property of multiplication ϭ 32y Multiply 4 and 8. Checkpoint Simplify the expression. 5. m ϩ 5 ϩ 9 6. 6(3k) 7. 4 ϩ x ϩ (Ϫ1) 8. (2r)(Ϫ5) Identity Properties When 0 is added to any number, or when any number is multiplied by 1, the result is identical to the original number. These properties of 0 and 1 are called identity properties, and the numbers 0 and 1 are called identities. Note Worthy Identity Properties In your notebook, be sure to Identity Property of Addition Identity Property of Multiplication include important properties such as those from this lesson. Words The sum of a number and the Words The product of a number and the You may find it helpful to write additive identity , 0, is the number. multiplicative identity , 1, is the number. each property using words, numbers, and algebra, as Numbers Ϫ6 ϩ 0 ϭ Ϫ6 Numbers 4 p 1 ϭ 4 shown at the right. Algebra a ϩ 0 ϭ a Algebra a p 1 ϭ a 64 Chapter 2 Solving Equations PAFL_229843_C0201.indd 64 12/17/08 12:22:35 PM Example 4 Identifying Properties Statement Property Illustrated a. (Ϫ5)(1) ϭ Ϫ5 Identity property of multiplication b. 2 (Ϫ9) ϭ Ϫ9 ϩ 2 Commutative property of addition c. y 2 ϩ 0 ϭ y 2 Identity property of addition d. 2(pq) ϭ (2p)q Associative property of multiplication Review Help Unit Analysis You can use unit analysis to find a conversion factor that To write the conversion factor converts a given measurement to different units. A conversion factor, 1 foot __ , you need to know 1 foot 12 inches such as __ , is equal to 1: 12 inches that 1 foot ϭ 12 inches. To 1 foot 12 inches __ ϭ __ 1 help you convert measures, 12 inches 12 inches see the Table of Measures on p. 793. So, the identity property of multiplication tells you that multiplying a measurement by a conversion factor does not change the measurement. Example 5 Multiplying by a Conversion Factor Roller Coasters The Steel Dragon 2000 is the world’s longest roller coaster. Its length is 2711 yards. How long is the roller coaster in feet? Solution 1 Find a conversion factor that converts yards to feet. The statement 1 yard ϭ 3 feet gives you two conversion factors. 1 yard 3 feet Factor 1: __ Factor 2: __ 3 feet 1 yard Unit analysis shows that a conversion factor that converts yards to feet has feet in the numerator and yards in the denominator: feet yards p _ ϭ feet yards So, factor 2 is the desired conversion factor. 2 Multiply the roller coaster’s length by factor 2 from Step 1. 3 feet Use the conversion factor. 2711 yards ϭ 2711 yards p __ 1 yard Divide out common unit. 8133 feet Multiply. The Steel Dragon 2000, located Answer The roller coaster is 8133 feet long. in Nagashima, Japan Checkpoint 9. Identify the property illustrated by the statement z 4 p 1 ϭ z 4 .
Load more

Recommended publications
  • Binocular Double Star Logbook
    Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club.
    [Show full text]
  • GTO Keypad Manual, V5.001
    ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN!
    [Show full text]
  • Legislators Hear Local Concerns for Upcoming Budget Session Progress
    SANDOVAL PLACITAS PRSRT-STD U.S. Postage Paid BERNALILLO Placitas, NM CORRALES Permit #3 SANDOVAL Postal Customer or COUNTY Current Resident SignPOSt ECRWSS NEW MEXICO A N I NDEPENDENT L OCAL N EWSPAPER S INCE 1988 • VOL. 30 / NO .1 • JANUARY 2018 • FREE LLIS Progress on county oil E and gas ordinance hits ACK —J sudden U-turn ~BILL D IVEN The contentious and long-struggling attempt to impose zoning regulations on oil and gas devel- opment in rural Sandoval County devolved into uncertainty on a 4-1 vote in December. A month earlier, Sandoval County commis- sioners approved Commissioner David Heil’s amendments to a proposed ordinance and agreed to act on publishing the ordinance at their December 14 meeting. All passed on 4-1 votes. With a favorable vote on publishing legal notices, the commission would have been free to take final action on the ordinance on January 18, its one meeting scheduled for the month. Instead the wheels came off. Setting the stage was Planning Director Mike Springfield acknowledging the ordinance View of Sandias and Rio Grande from Coronado Historic Site in Bernalillo amended in November contained erroneous noise limits for well drilling and production. Those were shown as higher than those recom- Legislators hear local concerns for upcoming mended by the Planning and Zoning Commis- sion after a public hearing in September. That administrative error had been corrected in the budget session IVEN document presented as ready for publication on ~SIGNPOST STAFF D December 14. ILL As the season of good cheer ends, the Legislature Commissioner Jay Block, who said he just convenes.
    [Show full text]
  • The Electric Sun Hypothesis
    Basics of astrophysics revisited. II. Mass- luminosity- rotation relation for F, A, B, O and WR class stars Edgars Alksnis [email protected] Small volume statistics show, that luminosity of bright stars is proportional to their angular momentums of rotation when certain relation between stellar mass and stellar rotation speed is reached. Cause should be outside of standard stellar model. Concept allows strengthen hypotheses of 1) fast rotation of Wolf-Rayet stars and 2) low mass central black hole of the Milky Way. Keywords: mass-luminosity relation, stellar rotation, Wolf-Rayet stars, stellar angular momentum, Sagittarius A* mass, Sagittarius A* luminosity. In previous work (Alksnis, 2017) we have shown, that in slow rotating stars stellar luminosity is proportional to spin angular momentum of the star. This allows us to see, that there in fact are no stars outside of “main sequence” within stellar classes G, K and M. METHOD We have analyzed possible connection between stellar luminosity and stellar angular momentum in samples of most known F, A, B, O and WR class stars (tables 1-5). Stellar equatorial rotation speed (vsini) was used as main parameter of stellar rotation when possible. Several diverse data for one star were averaged. Zero stellar rotation speed was considered as an error and corresponding star has been not included in sample. RESULTS 2 F class star Relative Relative Luminosity, Relative M*R *eq mass, M radius, L rotation, L R eq HATP-6 1.29 1.46 3.55 2.950 2.28 α UMi B 1.39 1.38 3.90 38.573 26.18 Alpha Fornacis 1.33
    [Show full text]
  • The Magic Valley Astronomical Society Notes from the President February
    February Highlights Notes from the President Feb. 1st, 6:45 to 9:00 PM Our first general membership meeting for the New Year will be held at 7:00 P.M. on Satur- Family night telescope day the 12th of February, 2011. We will be meeting at the Herrett Center, on the College of viewing. Centennial Obs. Southern Idaho Campus. Admission: $1.50, free for children 6 and under. Free Tom Gilbertson will host our annual telescope workshop "I Have a New Telescope, Now with paid planetarium admis- What?" If you are new to the hobby or if you have new equipment that you would like as- sion. sistance in learning how to operate, please bring it along (as well as any instruction manu- als) and our members will be happy to provide you with whatever assistance is required. Feb 12th, 7:00 pm to mid- This event is open to the general public and we encourage non-members to join us for this night Monthly Membership evening. General Meeting and Monthly free star party. Members in attendance will pair off with new (or old) telescope owners during the break- out sessions and teach them how to operate their new telescope (or old). We could use a Feb 15th, 7:00 to 9:00 PM lot of help from our members, so that no one has to wait to be helped. We had a good turn Family night telescope out last year and we expect more this year as well. Following the meeting we will take viewing. Centennial Obs. everyone with their telescopes up to the Stargazer’s Deck at the Centennial Observatory Admission: $1.50, free for for a evening of observing.
    [Show full text]
  • Pulsation Velocity Curves for 3 Cepheid Variables
    Pulsation Velocity Curves for 3 Cepheid Variables Kevin B. Stevenson∗ Department of Astronomy, University of Western Ontario, London, ON, N6A 3K7, Canada ABSTRACT A total of 44 usable observations were made of three of the brightest Classical Cepheids in the sky, δ Cephei, η Aquilae and ζ Geminorum. In each exposure, four Fe I spectral lines in the 6250 A˚ region were normalized, converted to a velocity span, averaged, then fitted by a model. The resulting model parameters from each exposure were then used to create a pulsation velocity curve as a function of phase and without the use of a projection factor typically used in other techniques. Acceptable agreement is found in comparing the radial velocity curves with Barnes, Bersier and Nardetto. The amplitudes of radius variation, used in the Baade- Wesselink method, were determined to be 3.54 × 106, 4.59 × 106 and 4.75 × 106 km for δ Cephei, η Aquilae and ζ Geminorum, respectively. Keywords: Cepheid variables, Delta Cephei, Eta Aquilae, Zeta Geminorum, radial velocity, Baade-Wesselink 1. INTRODUCTION A Cepheid variable is a particular type of variable star, an intrinsic pulsating variable. The variability is caused by physical changes within the star itself which causes its radius to expand and contract periodically. This process is part of its natural evolution as it ages and occurs in the instability strip of the Hertzsprung-Russell (HR) Diagram. A Cepheid varies in luminosity and spectral type with a generally stable, well determined period. Once its period is known, the star’s absolute magnitude can be precisely determined using the following empirically derived relation: Mν = −2.76 log(Π) − 1.4, (1) where Mν is the absolute magnitude and Π is the period in days.
    [Show full text]
  • Feb 2016 Newsletter
    Volume21, Issue 7 NWASNEWS February 2016 Newsletter for the Wiltshire, Swindon, Beckington February, Astro Fest time. Astronomical Societies and Salisbury Plain Observing Group Firstly can I send a thankyou to Peter This Friday and Saturday sees the Astro- Chappell for late arranging and Owen Bra- fest in London at the Kensington Confer- Wiltshire Society Page 2 zell for standing in to give a talk tonight on ence and events centre. Swindon Stargazers 3 galaxy cluster. Owen is well qualified as a The talks are the key to this exhibition as deep sky observer, especially eyeball to Beckington and SPOG 4 the stands tend to be very cramped for eye piece! He has frequently come along space, and many suppliers can no longer to mass observing sessions, and is well Software list: Downloadable 4 afford to rent the space. Even so, they are software and apps. known to several members. across 3 floors and you do need to go One of Owen’s previous visits was at a with an idea of what you want to see and Space Place : Lonely galax- 6 Stargazing live event 3 years ago, but we MUST prebook talks on both days.9’00am ies. were rained of the field but the previous to 6pm, 8 talks each day. year we had a very full day… This year, Space News: 6-17 Some ideas of my favourite purchases Moon haloes, Curiosity thanks to more late coordination from the last year have been two mounts, one, the selfie, Why does the Earth Beeb we made a low key event for the Sky Watcher Star Traveller has been the rotate, Blue origin soft land- 15th, and had clear skies AND the use of tool for astrophotography I have been ing, Opportunity 4 years the Manger Barn at very short notice.
    [Show full text]
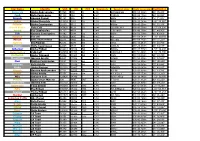
  • Star Name Identity SAO HD FK5 Magnitude Spectral Class Right Ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B
    Star Name Identity SAO HD FK5 Magnitude Spectral class Right ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B8IVpMnHg 00h 08,388m 29° 05,433' Caph Beta Cassiopeiae 21133 432 2 2,27 F2III-IV 00h 09,178m 59° 08,983' Algenib Gamma Pegasi 91781 886 7 2,83 B2IV 00h 13,237m 15° 11,017' Ankaa Alpha Phoenicis 215093 2261 12 2,39 K0III 00h 26,283m - 42° 18,367' Schedar Alpha Cassiopeiae 21609 3712 21 2,23 K0IIIa 00h 40,508m 56° 32,233' Deneb Kaitos Beta Ceti 147420 4128 22 2,04 G9.5IIICH-1 00h 43,590m - 17° 59,200' Achird Eta Cassiopeiae 21732 4614 3,44 F9V+dM0 00h 49,100m 57° 48,950' Tsih Gamma Cassiopeiae 11482 5394 32 2,47 B0IVe 00h 56,708m 60° 43,000' Haratan Eta ceti 147632 6805 40 3,45 K1 01h 08,583m - 10° 10,933' Mirach Beta Andromedae 54471 6860 42 2,06 M0+IIIa 01h 09,732m 35° 37,233' Alpherg Eta Piscium 92484 9270 50 3,62 G8III 01h 13,483m 15° 20,750' Rukbah Delta Cassiopeiae 22268 8538 48 2,66 A5III-IV 01h 25,817m 60° 14,117' Achernar Alpha Eridani 232481 10144 54 0,46 B3Vpe 01h 37,715m - 57° 14,200' Baten Kaitos Zeta Ceti 148059 11353 62 3,74 K0IIIBa0.1 01h 51,460m - 10° 20,100' Mothallah Alpha Trianguli 74996 11443 64 3,41 F6IV 01h 53,082m 29° 34,733' Mesarthim Gamma Arietis 92681 11502 3,88 A1pSi 01h 53,530m 19° 17,617' Navi Epsilon Cassiopeiae 12031 11415 63 3,38 B3III 01h 54,395m 63° 40,200' Sheratan Beta Arietis 75012 11636 66 2,64 A5V 01h 54,640m 20° 48,483' Risha Alpha Piscium 110291 12447 3,79 A0pSiSr 02h 02,047m 02° 45,817' Almach Gamma Andromedae 37734 12533 73 2,26 K3-IIb 02h 03,900m 42° 19,783' Hamal Alpha
    [Show full text]
  • The Skyscraper 2008 01.Indd
    The Skyscraper Vol. 35 no. 1 The monthly publication of The Skyscraper January 2008 January Meeting & Member Presentations FRIDAY, JANUARY 4TH AT NORTH SCITUATE COMMUNITY CENTER Remote and Robotic Observatories, Observe While You Sleep by Bob Napier Amateur Astronomical Society of Rhode Island 3D Astronomy presentation by Gerry Dyck 47 Peeptoad Road North Scituate, RI 02857 40 Years of Comet Observing www.theskyscrapers.org by Rick Lynch President Glenn Jackson DIRECTIONS TO THE COMMUNITY CENTER: From Seagrave Observatory: North 1st Vice President Scituate Community Center is the first building on the right side going Steve Hubbard south on Rt. 116, after the intersection of Rt. 6 Bypass (also Rt. 101) and 2nd Vice President Rt. 116, in N. Scituate. Famous Pizza is on the corner of that intersection. Kathy Siok Parking is across the street from the Community Center. Secretary Nichole Mechnig ANUARY IN THIS ISSUE Treasurer J 2008 PRESIDENT’S MESSAGE 2 Jim Crawford 7:30PM January Meeting North Scituate Community Glenn Jackson F4RIDAY Members at Large Center METEOR SHOWER 2 Jim Brenek PROSPECTS FOR 2008 Joe Sarandrea 7:00PM Public Observing Night Dave Huestis Seagrave Observatory, WINTER DOUBLE STARS: 3 Trustees SATURDAY5 weather permitting GEMINI Tracey Haley Glenn Chaple Bob Horton 7:00PM Public Observing Night Jerry Jeffrey Seagrave Observatory, ULTRAVIOLET SURPRISE 4 PATRICK L. BARRY & TONY S12ATURDAY weather permitting Librarian PHILLIP S Tom Barbish 7:00PM Public Observing Night DECEMBER MEETING 5 Editor Seagrave Observatory, NOTES STEVE HUB B ARD Jim Hendrickson S19ATURDAY weather permitting TREASURER’S REPORT 5 7:00PM Public Observing Night See back page for directions to JIM CRAW FORD Seagrave Observatory, Seagrave Observatory.
    [Show full text]
  • How to Plot Variable Star Charts Using the AAVSO Variable Star Plotter by Barry Beaman (BBA) Last Updated: April 24, 2009
    How to Plot Variable Star Charts Using the AAVSO Variable Star Plotter By Barry Beaman (BBA) Last Updated: April 24, 2009 1. Open the AAVSO web page at www.aavso.org. 2. In the left column of the web page locate “Plot a Chart” under “Most Popular Pages” and left click on it. The VSP Interface page will appear. 3. At this time, if you don’t already have the “One Page Guide,” select it and print a copy. 4. For most of us, the next step is to enter the name of the variable star we want to observe. All the VSP is looking for is the abbreviated star name, i.e., r leo, v1339 cyg, or eps aur. No capitals or full names are needed and in some cases will not be recognized. For example, zet gem will produce a chart but zeta gem might not and zeta geminorum most certainly will not be recognized. Capitals will be recognized and produce charts, but are unnecessary. Also there are some stars whose names overlap and create confusion. For example, µ (Mu) Cephei would normally be entered as mu cep; however, there is a twelfth magnitude Cepheid variable in Cepheus that is named MU Cephei. To avoid this overlap, AAVSO has given µ Cephei the name designation of “ * mu cep.” Please note that there is a space between “*” and “mu.” There are a number of these overlapping conditions in the AAVSO Data Base and a list of corrected names is maintained in the AAVSO web page in the Validation page at http://www.aavso.org/observing/aids/080114-namechanges.txt.
    [Show full text]
  • The COLOUR of CREATION Observing and Astrophotography Targets “At a Glance” Guide
    The COLOUR of CREATION observing and astrophotography targets “at a glance” guide. (Naked eye, binoculars, small and “monster” scopes) Dear fellow amateur astronomer. Please note - this is a work in progress – compiled from several sources - and undoubtedly WILL contain inaccuracies. It would therefor be HIGHLY appreciated if readers would be so kind as to forward ANY corrections and/ or additions (as the document is still obviously incomplete) to: [email protected]. The document will be updated/ revised/ expanded* on a regular basis, replacing the existing document on the ASSA Pretoria website, as well as on the website: coloursofcreation.co.za . This is by no means intended to be a complete nor an exhaustive listing, but rather an “at a glance guide” (2nd column), that will hopefully assist in choosing or eliminating certain objects in a specific constellation for further research, to determine suitability for observation or astrophotography. There is NO copy right - download at will. Warm regards. JohanM. *Edition 1: June 2016 (“Pre-Karoo Star Party version”). “To me, one of the wonders and lures of astronomy is observing a galaxy… realizing you are detecting ancient photons, emitted by billions of stars, reduced to a magnitude below naked eye detection…lying at a distance beyond comprehension...” ASSA 100. (Auke Slotegraaf). Messier objects. Apparent size: degrees, arc minutes, arc seconds. Interesting info. AKA’s. Emphasis, correction. Coordinates, location. Stars, star groups, etc. Variable stars. Double stars. (Only a small number included. “Colourful Ds. descriptions” taken from the book by Sissy Haas). Carbon star. C Asterisma. (Including many “Streicher” objects, taken from Asterism.
    [Show full text]
  • Steve S. Vogt Refereed Publications 1
    Steve S. Vogt Refereed Publications 1. “Two Jovian-Mass Planets in Earthlike Orbits,” (S.E. Robinson, G. Laughlin, S.S. Vogt, D.A. Fischer, R.P. Butler, G.W. Marcy, G.W. Henry, P. Driscoll, G. Takeda, J.A. Johnson). ApJ, 670, in press. 2. “A Determination of the Spin-Orbit Alignment of the Anomalously Dense Planet Orbiting HD 149026,” (A.S. Wolf, G. Laughlin, G.W. Henry, D.A. Fischer, G. Marcy, P. Butler, S. Vogt). ApJ, 667, 549-556, 2007. 3. “Spin-Orbit Alignment for the Eccentric Exoplanet HD 147506b,” (J.N. Winn, J.A. Johnson, K.M.G. Peek, G.W. Marcy, G. Bakos, K. Enya, N. Narita, Y. Suto, E.L. Turner, and S.S. Vogt). ApJ, 665, L167–L170, 2007. 4. “Fourteen New Companions from the Keck and Lick Radial Velocity Survey Including Five Brown Dwarf Candidates,” (S.G. Patel, S.S. Vogt, G.W. Marcy, J.A. Johnson, D.A. Fischer, J.T. Wright, and R.P. Butler). ApJ, 665, 744–753, 2007. 5. “Retired A Stars and Their Companions: Exoplanets Orbiting Three Intermediate- Mass Subgiants,” (J.A. Johnson, D.A. Fischer, G.W. Marcy, J.T. Wright, P. Driscoll, R.P. Butler, S. Hekker, S. Reffert, and S.S. Vogt). ApJ, 665, 785–793, 2007. 6. “The M Dwarf GJ 436 and its Neptune-Mass Planet,” (H.L. Maness, G.W. Marcy, E.B. Ford, P.H. Hauschildt, A.T. Shreve, G.B. Basri, R.P. Butler, and S.S. Vogt). PASP, 119, 90–101, 2007. 7. “Four New Exoplanets and Hints of Additional Substellar Companions to Exoplanet Host Stars,” (J.T.
    [Show full text]