DOCSLIB.ORG

Nanotechnology for Materials Physical Chemistry for Nanotechnology

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nanotechnology for Materials Physical Chemistry for Nanotechnology Nanotechnology for Materials Physical Chemistry for Nanotechnology 9 Overview of colloidal nanoparticles: principles, fabrication, characterization, sensors 9 Intermolecular forces ¾ Metallic colloidal nanoparticles: interaction with solvent and substrates, plasmon resonance • Physics of bottom‐up nanofabrication: wetting, dewetting, self‐assembled monolayers, micelles, liquid crystals • Surface microscopy techniques (TEM, SEM, AFM, STM, KPM ) • Molecular modeling and simulation: Molecular Dynamics and Monte Carlo methods and applications 1 Surface forces 2 Interactions in colloids In colloids and surface science we are interested in the interaction between macroscopic bodies constituted by thousands of atoms, typillicallysphilherical partilicles and flat surfaces. The dominant forces between the constituting atoms are: ‐ dispersion forces (van der Waals, depend on the density of atoms near the surface, ATTRACTIVE ) ‐ ionic forces (due to the surface charges, depend on the number of surface atoms and on the charge density at the surface, REPULSIVE) Assuming addit iv ity of forces, it is possibleto calculate the relevant interaction by integrating on the contribution of each atom. 3 PART 1 Van der Waals forces in collo ids 4 van der Waals forces between surfaces 5 6 Hamaker constant 7 Hamaker constant 8 Hamaker constant calculation: a microscopic approach For the van der Waals interaction the potential between two atoms or molecules 1 and 2 : where is the interaction constant as defined by London and is specific to the identity of the interacting atoms (C6 ∝ α1*α2. Hamaker then performed the integration of the interaction potential to calculate the total interaction between two macroscopic bodies. This then allows the total force between two arbitrarily shaped bodies to be given by: And the Hamaker constant is The Hamaker constant has units of energy and is the multiplicative factor of the distance‐dependent functions. Other geometrical constant often appears to make H (or A) transferable between the different possible geometries. 9 Hamaker constant calculation 1) Choose themathemati ca l form of the itintera tom ic/ ii/ionic/ molecular potential, w(r) (e.g. assume an arbitrary power law: w(r)=‐Cr ‐n ) 2) Set up the geometry of the particular interaction being derived 3) Assume "pairwise additivity"; i.e. the net interaction energy of a body is the sum of the individual interatomic/intermolecular interactions of the constituent atoms or molecules which make up that body 4) A solid continuum exists : the summation is replaced by an integration over the volumes of the interacting bodies assuming a number density of atoms/molecules/m3, ρ 5) Constant material properties : ρ and C are constant over the volume of the bodies→ volume integration : W12(D)= ∫∫∫w12(r) ρ1 ρ2 dV1dV2 10 Hamaker constant calculation: atom‐surface 11 Hamaker constant calculation: atom‐surface 12 Hamaker constant calculation: two planar surfaces 13 Hamaker constant calculation: two planar surfaces 14 Hamaker constant calculation: two spheres 15 Summary of common Hamaker interactions 16 Exercise U(a)=‐CH r/6 a = ‐CH d/12 a F(a) = ‐dU/da 17 Strength of VdW forces 2 V=‐AH/12π h per unit area 18 Strength of VdW forces: gecko 19 NATURE |VOL 405 | 8 JUNE 2000 |www.nature.com Geckos are exceptional in their ability to climb rapidly up smooth vertical surfaces. Microscopy has shown that a gecko's foot has nearly five hundred thousand keratinous hairs or setae. Each 30± 130μmlongsetaisonlyone‐ tenth the diameter of a human hair and contains hundreds of projections terminating in 0.2±0.5μmspatula‐shaped structures2. After nearly a century of anatomical description, here we report the first direct measurements of single setal force by using a two‐dimensional micro‐ electromechanical systems force sensor and a wire as a force gauge. Measurements revealed that a seta is ten times more effective at adhesion than predicted from maximal estimates on whole animals. Adhesive force values support the hypothesis that individual seta operate by van der Waals forces. Suitably orientated setae reduced the forces necessary to peel the toe by simply detaching above a critical angle with the substratum. 20 21 Gecko spatulae adhesion force Thesolid line representsasetawith spatltulae projtijecting tdtoward thesurface. The dashed line represents the setal force with spatulae projecting away from the surface 22 The structure similarity between the cross‐section views of the VA‐MWNTs (left) and gecko’s aligned elastic hairs (right). A book of 1480 g in weight suspended from a glass surface with use of vertically aligned‐MWNTs supported on a silicon wafer. The top right squared area shows the VA‐ MWNT array film, 4 mm by 4 mm 23 The effect of the liquid medium The medium between two interacting bodies has the net effect of reducing the attractive interaction with respect to vacuum. The extent depends on the dielectric properties of all themedia ildinvolved. 24 Medium effect: like particles 25 Medium effect: unlike particles Lorentz‐Berthelot rule 26 Summary of Vdw forces between colloids • Van der Waals forces in solvents are always attractive for particles of the same material • Approximate macroscopic interaction equations can be derived for different geometries (particle/surface 1 – medium 2‐ particle/surface 3) n • Equations have the form Energy = A123 * f / r A: Hamaker constant, depends on materials 1,2,3 f: geometric factor; n lower than 6 (typically 1 or 3) • The medium (2) has a strong influence on A: higher dielectric constant <‐>lowerHamakerconstant (even negative if 1/=3) • Tabulated Hamaker constants and equations can be useful in understanding the forces acting between your nanoparticles and substrates 27 PART 2 Dielectric permittivity (the medium between the nanopp)articles) 28 Dielectric constant (permittivity) 29 The effect of the liquid medium VACUUM VACUUM 30 The effect of the liquid medium 31 The effect of the liquid medium 32 The effect of the liquid medium Molecular permanent and induced dipoles DIELECTRIC produce local fields in the opposite direction εD > ε0 wrt the applied field 33 Contributions to permittivity: polarization 34 Dipoles in electric field • Thestrengthofthefieldatagivenpointisdefinedasthe force that would be exerted on a positive test charge of +1 coulblomb pldlaced at tha t poitint; the direc tion of the field is given by the direction of that force. • The definition of dipole orientation is instead from the negative to the positive charge From Coulomb’s law and theabove definitions, it follows that Energy = ‐ E • μ = ‐ E μ cos θ where θ is the angle μ between the two vectors 35 Polarization/2 36 Polarization/3 37 Polarization/4 38 Polarizability Let’s consider a spherical atom. In absence of external field the average charge density has a spherical symmetry centered at the nucleus. Appl yin g a field E the electron cloud will be distorted and attracted to the positive pole of the field, while the nucleus to the negative one, giving rise to the so called induced dipole. 39 Origin of polarizability/1 The nucleus has a point charge +Ze, while the electrons with total charge –Ze are uniformly distributed on the atomic volume, Electron density: We try now to evaluate quantitatively the equal and opposite forces that act on electrons and nuclei when they separate of a distance d in presence of an external field. 40 Origin of polarizability/2 Force acting on the nucleus due to the field: At the equilibrium distance d, this force will be balanced by the force exerted by the electrons on the nucleus. As the field due to a hollow charged sphere is 0 (cf Faraday cage/shield), only the electron charge inside the sphere of radius d has to be taken into account: A spherical charge distribution can be treated as a point charge, hence from Coulomb’ s law: 41 Origin of polarizability/3 Now we can equalize the two forces: The law obtained is the electrical analogous to Hooke’s law: F=‐kd ‐> F = (Drude oscillator) the distance of equilibrium is: and the induce dipole is μ∗ The total polarization (total dipole per unit of volume) for such a material is therefore ∗ 3 P = Σ μ /V = (Natoms/V)4πε0 R E = (Natoms/V)αE 3 where α= 4πε0 R is the atomic polarizability and E is the LOCAL field 42 Summary of polarization effects DIPOLE POLARIZABILITY Electronic polarization (polarizability) Orientational polarization (permanent dipoles) Ionic polarization (ionic solids) 43 The response to electric fields The electric displacement field,denotedasD, is a vector field that appears in Maxwell's equations. It accounts for the effects of free charges within materials. "D" stands for "displacement," as in the related concept of displacement current in dielectrics. In a linear, homogeneous, isotropic dielectric with instantaneous response to changes in the electric field, the polarization P depends linearly on the electric field, P = ε0 (εr‐1) E, D= ε0 εr E As opposed to the response of a vacuum, the response of normal materials to external fields generally depends on the frequency of the field. This frequency dependence reflects the fact that a material's polarization does not respond instantaneously to an applied field. 44 Micro‐macro equations for static permittivity “Lorentz local field:” Eloc =(εr+2)/3 Eext (takes into account that the field inside the dielectric is different from the external field) Macro: P = ε0 (εr‐1) Eext Micro: P = (N/V)αEloc = (N/V)α (εr+2)/3 Eext Combining the two equations: Clausius‐Mossotti: (εr‐1)/(εr+2) = (N/V)αelectronic /(3ε0) 2 Debye: (εr‐1)/(εr+2) = (N/V)(αelectronic +μ permanent/3kT)/ (3ε0) ‐> εr=(2k+1)/(1‐k) with k depending on molecular properties More complex and accurate: Onsager, Kirkwood and Fröhlich 45 Dielectric constants of common materials 46 Dielectric constants of organic solvents 47 Exercise: the effect of polarizability Calculate the dielectric constant for nitrogen gas (N2), composed by atoms with radius=0.8 Å, having a density = 1.251 g/L, and molllecular weihtight 28 g/l/mol.
Load more

Recommended publications
  • Subsurface Science
    Subsurface Science H. Levine G. MacDonald O. Rothaus M. Ruderman ~5_io__ n __ F_o __ r ____~.1 , __ J S. Treiman NTIS CRA&I ~ E. Williams OTIC TAB Ulldnfl0U'lCed J li s tifica tion In collaboration with: By ........... _._ ... _.... _...... ____ ._ .. ______ J ]. Banfield Distribution I R. Colwell r------------------ Avcilab!li~y (oces B. Ensley t-------;---------- .--.--- Avail21lCJioi D. Galas Oist ;:.pecial July 1995 JSR-94-330 Approved for public release; distribution unlimited. JASON The MITRE Corporation 7525 Coishire Drive Mclean, Vrrginia 22102-3481 (703) 883-6997 Form Approved REPORT DOCUMENTATION PAGE OM8 No. 0704·0188 PUblIC reporting burden for thiS collection of Information estimated to average 1 hour per response. includmg the time for review instructions, searc hing eXisting data sources, gathering and maintaining the data needed, and completing and revieWing the collection of information. Send comments regarding thls burden estimate or any other aspect of this collection of information, including suggestions for reducing thiS burden, to Washington Headquarte~ Services, Directorate for Information Operations and Reports. 1215 Jefferson DaviS Highway. Suite 1204, Arlington, VA 22202-4302. and to the Office of Management and Budget. Paperwork. Reduction Project (0704-0188), Washington, OC 20503, 1. AGENCY USE ONLY (LeavB blank) r. REPORT DATE 13. REPORT TYPE AND DATES COVERED July 25, 1995 4. TITLE AND SUBTITLE s. FUNDING NUMBERS SUBSURFACE SCIENCE 04-958534-01 6.~~OR(S). vme, G. MacDonald, O. Rot h aus, M. Ru d erman, S. Trelman,. E. Williams. In collaboration with: J. Banfield, R. Colwell, B. Ensley, D. Galas 7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES) 8.
    [Show full text]
  • UCLA Electronic Theses and Dissertations
    UCLA UCLA Electronic Theses and Dissertations Title Achieving Uniform Nanoparticle Dispersion in Metal Matrix Nanocomposites Permalink https://escholarship.org/uc/item/91r0q1x9 Author Xu, Jiaquan Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA Los Angeles Achieving Uniform Nanoparticle Dispersion in Metal Matrix Nanocomposites A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Materials Science and Engineering by Jiaquan Xu 2015 © Copyright by Jiaquan Xu 2015 ABSTRACT OF THE DISSERTATION Achieving Uniform Nanoparticle Dispersion in Metal Matrix Nanocomposites By Jiaquan Xu Doctor of Philosophy in Materials Science and Engineering University of California, Los Angeles, 2015 Professor Xiaochun Li, Co-Chair Professor Jenn-Ming Yang, Co-Chair The objective of this study is to gain fundamental knowledge on the interactions between nanoparticles to achieve a uniform dispersion of nanoparticles in metals for manufacturing metal matrix nanocomposites (MMNCs). MMNC, also known as nanoparticles reinforced metal, is an emerging class of materials exhibiting unusual mechanical, physical, and chemical properties. However, a lack of fundamental knowledge and technology on how to achieve a uniform nanoparticle dispersion in MMNCs has hindered the rapid development of the MMNC field. In ii this dissertation, several methods were explored to achieve a uniform nanoparticle dispersion in MMNCs. In-situ oxidation method were applied to fabricate Al-Al2O3 nanocomposites with a uniform dispersion of Al2O3 nanoparticles. Pure Al nanoparticles were cold compressed in a steel mold and then melted in an alumina container. Al2O3 nanoparticles were in situ synthesized through the oxidation of the Al nanoparticle surfaces to form bulk Al nanocomposites during the process.
    [Show full text]
  • A Review of Current and Planned Smooth Surface Technologies for Fouling Resistance in Boiler
    MATERIAL- OCH KEMITEKNIK 1232 Smooth Surfaces: A review of current and planned smooth surface technologies for fouling resistance in boiler Robert Corkery, Linda Bäfver, Kent Davidsson, Adam Feiler Smooth Surfaces: A review of current and planned smooth surface technologies for fouling resistance in boiler. Glatta ytor: En genomgång av glatta ytor som teknik för att stå emot bildning av beläggningar på värmeöverförande ytor. Robert Corkery, Linda Bäfver, Kent Davidsson, Adam Feiler M08-838 VÄRMEFORSK Service AB 101 53 STOCKHOLM · Tel 08-677 25 80 Februari 2012 ISSN 1653-1248 VÄRMEFORSK Abstract Here we have described the basics of boilers, fuels, combustion, flue gas composition and mechanisms of deposition. We have reviewed coating technologies for boiler tubes, including their materials compositions, nanostructures and performances. The surface forces in boilers, in particular those relevant to formation of unwanted deposits in boilers have also been reviewed, and some comparative calculations have been included to indicate the procedures needed for further study. Finally practical recommendations on the important considerations in minimizing deposition on boiler surfaces are made. i VÄRMEFORSK ii VÄRMEFORSK Sammanfattning Det höga innehållet av alkali (kalium och natrium) och klor i avfall och biobränsle leder till drift- och underhållsproblem genom bildning av påslag och efterföljande korrosion på överhettare i förbränningsanläggningar. Detta projekt handlar om interaktioner på överhettartubers ytor vid förbränning av avfall och biobränsle. En genomlysning av tekniker som kan användas för att skapa glatta tubytor i pannor presenteras. Glatta ytor skall förhindra eller fördröja bildning av påslag. Påslag består av askelement från bränslet. Vid överhettare är kaliumklorid särskilt kritiskt och vid avfallsförbränning även natriumklorid.
    [Show full text]
  • Non-Covalent Short Range Interactions
    WORKSHOP Nanoscience on the Tip Non-Covalent Short Range Interactions Table of Contents: 1. Motivation ............................................................................................................ 1 2. Short Range Interactions and Surface Forces ...................................................... 1 3. Van der Waals Interactions for Point Interactions ............................................... 3 4. Surface Forces...................................................................................................... 4 5. Hamaker Constant................................................................................................ 5 6. Van der Waals Retardation Effects ...................................................................... 6 7. Adhesion and Surface Energies............................................................................ 6 8. Cutoff Distance for Van der Waals Calculations................................................. 7 9. Capillary Forces due to Vapor Condensation ...................................................... 8 10. Critical Humidity for Capillary Neck Formation................................................. 9 11. Estimation of the Tip Radius Utilizing the Capillary Effects ............................10 12. Modification of Hydrophobicity (Wettability)................................................... 12 13. Force Displacement Curves ............................................................................... 13 References ................................................................................................................
    [Show full text]
  • Multistable Interaction Between a Spherical Brownian Particle and an Air–Water Interface Stefano Villa, Antonio Stocco, Christophe Blanc, Maurizio Nobili
    Multistable interaction between a spherical Brownian particle and an air–water interface Stefano Villa, Antonio Stocco, Christophe Blanc, Maurizio Nobili To cite this version: Stefano Villa, Antonio Stocco, Christophe Blanc, Maurizio Nobili. Multistable interaction between a spherical Brownian particle and an air–water interface. Soft Matter, Royal Society of Chemistry, 2020, 16, pp.960. 10.1039/C9SM01472A. hal-02460100 HAL Id: hal-02460100 https://hal.archives-ouvertes.fr/hal-02460100 Submitted on 23 Sep 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Journal Name Multistable Interaction between a Spherical Brownian Particle and an Air-Water Interface Stefano Villa,a Antonio Stocco,b Christophe Blanc,a and Maurizio Nobili∗a We report the measurement of the interaction energy between a charged Brownian polystyrene particle and an air-water interface. The interaction potential is obtained from Boltzmann equation by tracking particle interface distance with a specifically designed Dual-Wave Reflection Interfer- ence Microscopy (DW-RIM) setup. The particle has two equilibrium positions located at few hun- dreds of nanometers from the interface. The farthest position is well accounted by a DLVO model complemented by gravity. The closest one, not predicted by current models, more frequently ap- pears in water solutions at relatively high ions concentrations, when electrostatic interaction is screened out.
    [Show full text]
  • Origins and Applications of London Dispersion Forces and Hamaker Constants in Ceramics
    journal J. Am. Ceram. Soc., 83 [9] 2117–46 (2000) Origins and Applications of London Dispersion Forces and Hamaker Constants in Ceramics Roger H. French*,** Central Research, DuPont Company, Wilmington, Delaware 19880; and Materials Science Department, University of Pennsylvania, Philadelphia, Pennsylvania 19104 The London dispersion forces, along with the Debye and Keesom forces, constitute the long-range van der Waals forces. Article Table of Contents London’s and Hamaker’s work on the point-to-point disper- sion interaction and Lifshitz’s development of the continuum Introduction 2118 theory of dispersion are the foundations of our understanding Overview 2118 of dispersion forces. Dispersion forces are present for all History 2118 materials and are intrinsically related to the optical properties Structure of This Article 2119 and the underlying interband electronic structures of materi- Origins of Dispersion Forces 2119 als. The force law scaling constant of the dispersion force, van der Waals Forces 2119 known as the Hamaker constant, can be determined from Lifshitz Theory and Electronic Structure and spectral or parametric optical properties of materials, com- Bonding 2121 bined with knowledge of the configuration of the materials. Full Spectral Nonretarded Hamaker Constant ANR With recent access to new experimental and ab initio tools for from Spectral Optical Properties 2125 determination of optical properties of materials, dispersion Methods for Estimating Hamaker force research has new opportunities for detailed studies. Constant ANR 2128 Opportunities include development of improved index approx- Retardation of Dispersion Forces and the Retarded imations and parametric representations of the optical prop- Hamaker Constant AR 2129 erties for estimation of Hamaker constants.
    [Show full text]
  • In Situ Characterization of Nanoscale Contaminations Adsorbed in Air Using Atomic Force Microscopy
    In situ characterization of nanoscale contaminations adsorbed in air using atomic force microscopy Jesús S. Lacasa1, Lisa Almonte1,2 and Jaime Colchero*1 Full Research Paper Open Access Address: Beilstein J. Nanotechnol. 2018, 9, 2925–2935. 1Centro de Investigación en Óptica y Nanofísica (CIOyN), doi:10.3762/bjnano.9.271 Departamento Física, Facultad de Química, Campus Espinardo, Universidad de Murcia, 30100 Murcia, Spain and 2Electrical Received: 05 September 2018 Engineering and Biological Science, University of Notre Dame, Notre Accepted: 01 November 2018 Dame, Indiana 46556, USA Published: 23 November 2018 Email: Associate Editor: J. Frommer Jaime Colchero* - [email protected] © 2018 Lacasa et al.; licensee Beilstein-Institut. * Corresponding author License and terms: see end of document. Keywords: atomic force microscopy; cantilever; contact potential; electrostatic forces; force spectroscopy; Hamaker constant; Kelvin probe microscopy; surface contamination; tip cleaning; tip–sample interaction; van der Waals interaction Abstract Under ambient conditions, surfaces are rapidly modified and contaminated by absorbance of molecules and a variety of nanoparti- cles that drastically change their chemical and physical properties. The atomic force microscope tip–sample system can be consid- ered a model system for investigating a variety of nanoscale phenomena. In the present work we use atomic force microscopy to directly image nanoscale contamination on surfaces, and to characterize this contamination by using multidimensional spectrosco- py techniques. By acquisition of spectroscopy data as a function of tip–sample voltage and tip–sample distance, we are able to de- termine the contact potential, the Hamaker constant and the effective thickness of the dielectric layer within the tip–sample system.
    [Show full text]
  • Transport, Retention, and Long-Term Release Behavior of Zno Nanoparticle Aggregates in Saturated Quartz Sand: Role of Solution Ph and Biofilm Coating
    Water Research 90 (2016) 247e257 Contents lists available at ScienceDirect Water Research journal homepage: www.elsevier.com/locate/watres Transport, retention, and long-term release behavior of ZnO nanoparticle aggregates in saturated quartz sand: Role of solution pH and biofilm coating Yosep Han a, 1, Gukhwa Hwang a, 1, Donghyun Kim a, Scott A. Bradford b, * Byoungcheun Lee c, Igchun Eom c, Pil Je Kim c, Siyoung Q. Choi d, Hyunjung Kim a, a Department of Mineral Resources and Energy Engineering, Chonbuk National University, Jeonju, Jeonbuk 561-756, Republic of Korea b USDA, ARS, US Salinity Laboratory, Riverside, CA 92507, USA c Risk Assessment Division, National Institute of Environmental Research, Hwangyeong-ro 42, Seo-gu, Incheon 404-708, Republic of Korea d Department of Chemical and Biomolecular Engineering, KAIST, Daejeon 305-701, Republic of Korea article info abstract Article history: The transport, retention, and long-term release of zinc oxide nanoparticle aggregates (denoted below as Received 24 August 2015 ZnO-NPs) were investigated in saturated, bare and biofilm (Pseudomonas putida) coated sand packed Received in revised form columns. Almost complete retention of ZnO-NPs occurred in bare and biofilm coated sand when the 21 November 2015 influent solution pH was 9 and the ionic strength (IS) was 0.1 or 10 mM NaCl, and the retention profiles Accepted 6 December 2015 were always hyper-exponential. Increasing the solution IS and biofilm coating produced enhanced Available online 17 December 2015 retention of ZnO-NPs near the column inlet. The enhanced NPs retention at high IS was attributed to more favorable NP-silica and NP-NP interactions; this was consistent with the interaction energy cal- Keywords: fi ZnO nanoparticle aggregates culations.
    [Show full text]
  • Particle Interactions at the Nanoscale
    Particle interactions at the nanoscale From colloidal processing to self-assembled arrays. Bertrand Faure Doctoral Thesis 2012 Department of Materials and Environmental Chemistry Arrhenius Laboratory, Stockholm University SE-106 91 Stockholm, Sweden Faculty opponent Prof. Albert Philipse Van’t Hoff Laboratory for Physical and Colloid Chemistry Utrecht University, The Netherlands Evaluation committee Prof. Johan Bergenholtz Department of Chemistry and Molecular Biology University of Gothenburg, Sweden Prof. Hans Ågren Department of Theoretical Chemistry Royal Institute of Technology, Stockholm, Sweden Prof. Maria Strømme Department of Engineering Sciences, Ångström Laboratory Uppsala University, Sweden Substitute Assoc. Prof. Junliang Sun Department of Materials and Environmental Chemistry Stockholm University, Sweden Cover page: Macro photograph of a ferrofluid in a magnetic field, published by Thomas Sahan under the CCBY 3.0 license. http://commons.wikimedia.org/wiki/File:Ferrofluid_close.jpg © Bertrand Faure, Stockholm 2012 All rights reserved. No parts of this thesis may be reproduced without permission from the author. ISBN 978-91-7447-570-8 Printed in Sweden by US-AB, Stockholm 2012 Distributor: Department of Materials and Environmental Chemistry, Stockholm University, Sweden Pour Amélie, Manon et Élise. Abstract Nanostructured materials are the next generation of high-performance ma- terials, harnessing the novel properties of their nanosized constituents. The controlled assembly of nanosized particles and the design of the optimal nanostructure require a detailed understanding of particle interactions and robust methods to tune them. This thesis describes innovative approaches to these challenges, relating to the determination of Hamaker constants for iron oxide nanoparticles, the packaging of nanopowders into redispersible gran- ules, the tuning of the wetting behavior of nanocrystals and the simulation of collective magnetic properties in arrays of superparamagnetic nanoparticles.
    [Show full text]
  • A Fundamental Adhesion Model for Asphalt
    KTH Architecture and the Built Environment A Fundamental Adhesion Model for Asphalt Åsa Laurell Lyne KTH Royal Institute of Technology School of Architecture and the Built Environment Department of Transport Science Division of Highway and Railway Engineering SE-100 44 Stockholm Doctoral Thesis Stockholm, Sweden 2014 Åsa Laurell Lyne Doctoral thesis Division of Highway and Railway Engineering Department of Transport Science TRITA-TSC-PHD 14-004 ISBN 978-91-87353-42-0 Preface This doctoral thesis is based on research performed during 2009 – 2014, at the Division of Highway and Railway Engineering, Department of Transport Science, KTH Royal Institute of Technology in Stockholm, Sweden. The main aim of this thesis was to deliver an improved understanding of the mechanism of bonding of un-aged bitumen to aggregates, with and without the addition of Portland cement, and to provide a fundamental understanding for the development of a new test method for bitumen-aggregate adhesion. I would like to start with expressing my gratitude to my main supervisor Professor Björn Birgisson for initiating this project, providing a meaningful challenge, for his great support, valuable comments, never-ending patience and for encourage me to take a non-traditional approach in a well-researched field. The Development Fund of the Swedish Construction Industry (SBUF), the Swedish Transport Administration (Trafikverket) and BVFF via the Swedish Transport Administration are gratefully acknowledged for financial support. I am also sincerely grateful to Mr. Måns Collin and Docent Per Redelius for guiding me through this work and making sure that this project would have commercial relevance. Thanks to Mr.
    [Show full text]
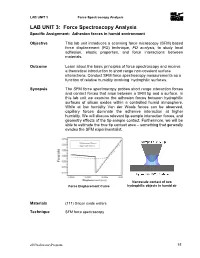
  • LAB UNIT 3: Force Spectroscopy Analysis Specific Assignment: Adhesion Forces in Humid Environment
    LAB UNIT 3 Force Spectroscopy Analysis LAB UNIT 3: Force Spectroscopy Analysis Specific Assignment: Adhesion forces in humid environment Objective This lab unit introduces a scanning force microscopy (SFM) based force displacement (FD) technique, FD analysis, to study local adhesion, elastic properties, and force interactions between materials. Outcome Learn about the basic principles of force spectroscopy and receive a theoretical introduction to short range non-covalent surface interactions. Conduct SFM force spectroscopy measurements as a function of relative humidity involving hydrophilic surfaces. Synopsis The SFM force spectroscopy probes short range interaction forces and contact forces that arise between a SFM tip and a surface. In this lab unit we examine the adhesion forces between hydrophilic surfaces of silicon oxides within a controlled humid atmosphere. While at low humidity Van der Waals forces can be observed, capillary forces dominate the adhesive interaction at higher humidity. We will discuss relevant tip-sample interaction forces, and geometry effects of the tip-sample contact. Furthermore, we will be able to estimate the true tip contact area – something that generally evades the SFM experimentalist. Nanoscale contact of two Force Displacement Curve hydrophilic objects in humid air Materials (111) Silicon oxide wafers Technique SFM force spectroscopy 2009LaboratoryProgram 55 LAB UNIT 3 Force Spectroscopy Analysis Table of Contents 1. Assignment..................................................................................................
    [Show full text]
  • Interaction Between Colloidal Particles Literature Review
    Interaction between colloidal Technical Report TR-10-26 particles – Literature Review Interaction between colloidal particles Literature Review Longcheng Liu and Ivars Neretnieks Department of Chemical Engineering and Technology Royal Institute of Technology February 2010 Svensk Kärnbränslehantering AB Swedish Nuclear Fuel and Waste Management Co Box 250, SE-101 24 Stockholm Phone +46 8 459 84 00 TR-10-26 CM Gruppen AB, Bromma, 2010 CM Gruppen ISSN 1404-0344 Tänd ett lager: SKB TR-10-26 P, R eller TR. Interaction between colloidal particles Literature Review Longcheng Liu and Ivars Neretnieks Department of Chemical Engineering and Technology Royal Institute of Technology February 2010 This report concerns a study which was conducted for SKB. The conclusions and viewpoints presented in the report are those of the authors. SKB may draw modified conclusions, based on additional literature sources and/or expert opinions. A pdf version of this document can be downloaded from www.skb.se. Abstract This report summarises the commonly accepted theoretical basis describing interaction between colloidal particles in an electrolyte solution. The two main forces involved are the van der Waals attractive force and the electrical repulsive force. The report describes in some depth the origin of these two forces, how they are formulated mathematically as well as how they interact to sometimes result in attraction and sometimes in repulsion between particles. The report also addresses how the mathematical models can be used to quantify the forces and under which conditions the models can be expected to give fair description of the colloidal system and when the models are not useful.
    [Show full text]