Going in Circles Is the Way Forward: the Role of Recurrence in Visual Inference Van Bergen and Kriegeskorte 177
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Artist/Group Song Title
ARTIST/GROUP SONG TITLE V.I.C. WOBBLE VALENS, RICHIE DONNA VALENS, RITCHIE COME ON LET'S GO VALLI, FRANKIE CAN'T TAKE MY EYES OFF YOU VALLI, FRANKIE MY EYES ADORED YOU VAN BEETHOVEN, CAMPER TAKE THE SKINHEADS BOWLING VAN DYKE, LEROY AUCTIONEER [THE] VAN DYKE, LEROY WALK ON BY VAN HALEN AIN'T TALKIN' 'BOUT LOVE VAN HALEN AND THE CRADLE WILL ROCK VAN HALEN BEAUTIFUL GIRLS VAN HALEN DANCE THE NIGHT AWAY VAN HALEN DON'T TELL ME (WHAT LOVE CAN DO) VAN HALEN DREAMS VAN HALEN EVERYBODY WANTS SOME (EXPLICIT) VAN HALEN FEEL YOUR LOVE TONIGHT VAN HALEN FINISH WHAT YA STARTED VAN HALEN HOT FOR TEACHER VAN HALEN HUMANS BEING VAN HALEN ICE CREAM MAN VAN HALEN I'LL WAIT VAN HALEN JAMIE'S CRYIN' VAN HALEN JUMP VAN HALEN OH, PRETTY WOMAN VAN HALEN PANAMA VAN HALEN POUNDCAKE VAN HALEN RIGHT NOW VAN HALEN RUNNIN' WITH THE DEVIL VAN HALEN TOP OF THE WORLD VAN HALEN UNCHAINED VAN HALEN WHEN IT'S LOVE VAN HALEN WHY CAN'T THIS BE LOVE VAN HALEN WITHOUT YOU VAN HALEN YOU REALLY GOT ME VAN SHELTON, RICKY BACKROADS VAN SHELTON, RICKY I AM A SIMPLE MAN VAN SHELTON, RICKY I MEANT EVERY WORD HE SAID VAN SHELTON, RICKY I'LL LEAVE THIS WORLD LOVING YOU VAN SHELTON, RICKY I'VE CRIED MY LAST TEAR FOR YOU VAN SHELTON, RICKY JUST AS I AM VAN SHELTON, RICKY KEEP IT BETWEEN THE LINES VAN SHELTON, RICKY LIFE TURNED HER THAT WAY VAN SHELTON, RICKY LIVING PROOF VAN SHELTON, RICKY LOLA'S LOVE VAN SHELTON, RICKY SHE NEEDS ME VAN SHELTON, RICKY SOMEBODY LIED VAN SHELTON, RICKY STATUE OF A FOOL VAN SHELTON, RICKY WEAR MY RING AROUND YOUR NECK VAN SHELTON, RICKY WHERE WAS I VAN -

Who's Who in Pop Record Production (1995)
WHO'S WHO IN POP RECORD PRODUCTION (1995) The following is a list of PRODUCERS credited on at least one album or one single in the Top Pop 100 Charts or that has been picked in our "Next On The Charts" section so far this year. (Please note that due to computer restraints, PRODUCERS are NOT credited on records that have more than 5 PRODUCERS listed) This listing includes the PRODUCER'S NAME (S= # singles) (LP= # Albums) - "Record Title"- ARTIST-/ and OTHER PRODUCERS on the record. 20 Fingers(S = 3)- "Fat Boy"- Max-A-MillionV 'Mr. Personality"- Gillette-/ "Lick It"- Ftoula-/ Cyrus EstebanfS = 1)- "I'll Be Around"- Rappin' 4-Tay & The SpinnersVFranky J Bryan Adams(S = 1)- "Have You Ever Really Loved A Woman?"-Bryan Adams-/Robert John 'Mutt' Lange Emilto EstefanfS = 2)- "Everlasting Love'-Gloria Estefan-/ Jorge Casas Lawrence Dermer "It's Too Walter Afanasieff (S = 4)- "Always And Forever'-Luther Vandross-/ Luther Vandross "All I Want ForLate'-Gloria Estefan-/ Jorge Casas Clay Ostwald Christmas'-Mariah Carey-/ Mariah Carey "Going In Circles'-Luther Vandross-/ "Wherever Would iMeliasa Etheridge(S= 1)- "If I Wanted To/Like The Way I Do'-Melissa EtheridgeVHugh Padgham Be"-Dusty Springfield & Daryl Hall-/ Tom Sh Face To Face(S = 1)- "Disconnected"- Face To Face-/Thom Wilson Matt Aitken(S = 1)- "Total Eclipse Of The Heart"-Nicki FrenchVJohn Springate Mike Stock (|_P= 1)- "Big Choice"- Face To FaceVThom Wilson Derek Allen(S = 1)- "Let's Do It Again"- Blackgirt-/ Bruce Fairbairn(S = 2)- "Don't Tell Me What Love Can Do"- Van Halen-/ "Can't Stop -

Karaoke Mietsystem Songlist
Karaoke Mietsystem Songlist Ein Karaokesystem der Firma Showtronic Solutions AG in Zusammenarbeit mit Karafun. Karaoke-Katalog Update vom: 13/10/2020 Singen Sie online auf www.karafun.de Gesamter Katalog TOP 50 Shallow - A Star is Born Take Me Home, Country Roads - John Denver Skandal im Sperrbezirk - Spider Murphy Gang Griechischer Wein - Udo Jürgens Verdammt, Ich Lieb' Dich - Matthias Reim Dancing Queen - ABBA Dance Monkey - Tones and I Breaking Free - High School Musical In The Ghetto - Elvis Presley Angels - Robbie Williams Hulapalu - Andreas Gabalier Someone Like You - Adele 99 Luftballons - Nena Tage wie diese - Die Toten Hosen Ring of Fire - Johnny Cash Lemon Tree - Fool's Garden Ohne Dich (schlaf' ich heut' nacht nicht ein) - You Are the Reason - Calum Scott Perfect - Ed Sheeran Münchener Freiheit Stand by Me - Ben E. King Im Wagen Vor Mir - Henry Valentino And Uschi Let It Go - Idina Menzel Can You Feel The Love Tonight - The Lion King Atemlos durch die Nacht - Helene Fischer Roller - Apache 207 Someone You Loved - Lewis Capaldi I Want It That Way - Backstreet Boys Über Sieben Brücken Musst Du Gehn - Peter Maffay Summer Of '69 - Bryan Adams Cordula grün - Die Draufgänger Tequila - The Champs ...Baby One More Time - Britney Spears All of Me - John Legend Barbie Girl - Aqua Chasing Cars - Snow Patrol My Way - Frank Sinatra Hallelujah - Alexandra Burke Aber Bitte Mit Sahne - Udo Jürgens Bohemian Rhapsody - Queen Wannabe - Spice Girls Schrei nach Liebe - Die Ärzte Can't Help Falling In Love - Elvis Presley Country Roads - Hermes House Band Westerland - Die Ärzte Warum hast du nicht nein gesagt - Roland Kaiser Ich war noch niemals in New York - Ich War Noch Marmor, Stein Und Eisen Bricht - Drafi Deutscher Zombie - The Cranberries Niemals In New York Ich wollte nie erwachsen sein (Nessajas Lied) - Don't Stop Believing - Journey EXPLICIT Kann Texte enthalten, die nicht für Kinder und Jugendliche geeignet sind. -

Songs by Title
Karaoke Song Book Songs by Title Title Artist Title Artist #1 Nelly 18 And Life Skid Row #1 Crush Garbage 18 'til I Die Adams, Bryan #Dream Lennon, John 18 Yellow Roses Darin, Bobby (doo Wop) That Thing Parody 19 2000 Gorillaz (I Hate) Everything About You Three Days Grace 19 2000 Gorrilaz (I Would Do) Anything For Love Meatloaf 19 Somethin' Mark Wills (If You're Not In It For Love) I'm Outta Here Twain, Shania 19 Somethin' Wills, Mark (I'm Not Your) Steppin' Stone Monkees, The 19 SOMETHING WILLS,MARK (Now & Then) There's A Fool Such As I Presley, Elvis 192000 Gorillaz (Our Love) Don't Throw It All Away Andy Gibb 1969 Stegall, Keith (Sitting On The) Dock Of The Bay Redding, Otis 1979 Smashing Pumpkins (Theme From) The Monkees Monkees, The 1982 Randy Travis (you Drive Me) Crazy Britney Spears 1982 Travis, Randy (Your Love Has Lifted Me) Higher And Higher Coolidge, Rita 1985 BOWLING FOR SOUP 03 Bonnie & Clyde Jay Z & Beyonce 1985 Bowling For Soup 03 Bonnie & Clyde Jay Z & Beyonce Knowles 1985 BOWLING FOR SOUP '03 Bonnie & Clyde Jay Z & Beyonce Knowles 1985 Bowling For Soup 03 Bonnie And Clyde Jay Z & Beyonce 1999 Prince 1 2 3 Estefan, Gloria 1999 Prince & Revolution 1 Thing Amerie 1999 Wilkinsons, The 1, 2, 3, 4, Sumpin' New Coolio 19Th Nervous Breakdown Rolling Stones, The 1,2 STEP CIARA & M. ELLIOTT 2 Become 1 Jewel 10 Days Late Third Eye Blind 2 Become 1 Spice Girls 10 Min Sorry We've Stopped Taking Requests 2 Become 1 Spice Girls, The 10 Min The Karaoke Show Is Over 2 Become One SPICE GIRLS 10 Min Welcome To Karaoke Show 2 Faced Louise 10 Out Of 10 Louchie Lou 2 Find U Jewel 10 Rounds With Jose Cuervo Byrd, Tracy 2 For The Show Trooper 10 Seconds Down Sugar Ray 2 Legit 2 Quit Hammer, M.C. -

U2 All Along the Watchtower U2 All Because of You U2 All I Want Is You U2 Angel of Harlem U2 Bad U2 Beautiful Day U2 Desire U2 D
U/z U2 All Along The Watchtower U2 All Because of You U2 All I Want Is You U2 Angel Of Harlem U2 Bad U2 Beautiful Day U2 Desire U2 Discotheque U2 Electrical Storm U2 Elevation U2 Even Better Than The Real Thing U2 Fly U2 Ground Beneath Her Feet U2 Hands That Built America U2 Haven't Found What I'm Looking For U2 Helter Skelter U2 Hold Me, Thrill Me, Kiss Me, Kill Me U2 I Still Haven't Found What I'm Looking For U2 I Will Follow U2 In A Little While U2 In Gods Country U2 Last Night On Earth U2 Lemon U2 Mothers Of The Disappeared U2 Mysterious Ways U2 New Year's Day U2 One U2 Please U2 Pride U2 Pride In The Name Of Love U2 Sometimes You Can't Make it on Your Own U2 Staring At The Sun U2 Stay U2 Stay Forever Close U2 Stuck In A Moment U2 Sunday Bloody Sunday U2 Sweetest Thing U2 Unforgettable Fire U2 Vertigo U2 Walk On U2 When Love Comes To Town U2 Where The Streets Have No Name U2 Who's Gonna Ride Your Wild Horses U2 Wild Honey U2 With Or Without You UB40 Breakfast In Bed UB40 Can't Help Falling In Love UB40 Cherry Oh Baby UB40 Cherry Oh Baby UB40 Come Back Darling UB40 Don't Break My Heart UB40 Don't Break My Heart UB40 Earth Dies Screaming UB40 Food For Thought UB40 Here I Am (Come And Take Me) UB40 Higher Ground UB40 Homely Girl UB40 I Got You Babe UB40 If It Happens Again UB40 I'll Be Yours Tonight UB40 King UB40 Kingston Town UB40 Light My Fire UB40 Many Rivers To Cross UB40 One In Ten UB40 Rat In Mi Kitchen UB40 Red Red Wine UB40 Sing Our Own Song UB40 Swing Low Sweet Chariot UB40 Tell Me Is It True UB40 Train Is Coming UB40 Until -

Songs by Title
Sound Master Entertianment Songs by Title smedenver.com Title Artist Title Artist #1 Nelly Spice Girls #1 Crush Garbage 2 In The Morning New Kids On The (Cable Car) Over My Head Fray Block (I Love You) What Can I Say Jerry Reed 2 Step Unk (I Wanna Hear) A Cheatin' Song Anita Cochran & 20 Good Reasons Thirsty Merc Conway Twitty 21 Questions 50 Cent (If You're Wondering If I Want Weezer 50 Cent & Nate Dogg You To) I Want You To 24 7 Kevon Edmonds (It's Been You) Right Down The Gerry Rafferty 24 Hours From Tulsa Gene Pitney Line 24's T.I. (I've Had) The Time Of My Life Bill Medley & Jennifer 25 Miles Edwin Starr Warnes 25 Or 6 To 4 Chicago (Just Like) Romeo & Juliet Reflections 26 Cents Wilkinsons (My Friends Are Gonna Be) Merle Haggard 29 Nights Danni Leigh Strangers 29 Palms Robert Plant (Reach Up For The) Sunrise Duran Duran 3 Britney Spears (Sittin' On) The Dock Of The Bay Michael Bolton 30 Days In The Hole Humble Pie Otis Redding 30,000 Pounds Of Bananas Harry Chapin (There's Gotta Be) More To Life Stacie Orrico 32 Flavors Alana Davis (When You Feel Like You're In Carl Smith Love) Don't Just Stand There 3am Matchbox Twenty (Who Discovered) America Ozomatli 4 + 20 Crosby, Stills, Nash & Young (You Never Can Tell) C'est La Emmylou Harris Vie 4 Ever Lil Mo & Fabolous (You Want To) Make A Memory Bon Jovi 4 In The Morning Gwen Stefani '03 Bonnie & Clyde Jay-Z & Beyonce 4 Minutes Avant 1, 2 Step Ciara & Missy Elliott 4 To 1 In Atlanta Tracy Byrd 1, 2, 3, 4 (I Love You) Plain White T's 409 Beach Boys 1,000 Faces Randy Montana 42nd Street 42nd Street 10 Days Late Third Eye Blind 45 Shinedown 100 Years Five For Fighting 455 Rocket Kathy Mattea 100% Chance Of Rain Gary Morris 4am Our Lady Peace 100% Pure Love Crystal Waters 5 Miles To Empty Brownstone 10th Ave. -

To Whom It May Concern, Re: BAHAMAS EARTHTONES
To whom it may concern, Re: BAHAMAS EARTHTONES Earthtones is the newest and totally most best album yet from Bahamas, aka me, Afie Jurvanen. I wasn't feeling too inspired in 2016. I’d been in a seemingly unbroken cycle of recording and touring for 6 years. I know, you're saying to yourself "that's so clichė, all musicians complain about being tired..." But wait, there's more! Not knowing exactly what type of album to make, I was feeling pretty low. But at that very moment, my longtime manager and confidante Robbie Lackritz called and said "dude, you should make an album with D'angelo's rhythm section." And just like that, the juices were flowing and the songs started coming. I wrote songs about having success, having kids, and having depression. I wrote songs about going on tour, going back in time and going in circles. I wrote songs about my other worldly wife, my jerk dad and my garbage relationship with my brother. Crazy right?! In Sept of 2016 I flew to Los Angeles and spent three days in the studio with the bass boss Pino Palladino and the titan of time keeping, Mr. James Gadson. No rehearsals, no charts, no rules. We worked fast and came away with 10 songs that sounded fresh and strange and warm and free of any genre. The results were so inspiring to me that I quickly pulled my road band (Felicity Williams, Christine Bougie, Darcy Yates, Jason Tait, Don Kerr) into a Prague studio to record a few more songs. -

GOING in CIRCLES MUSIC: Going in Circles by the Friends of Distinction (CD: Best Of)
JOHN ROBINSON | www.mrshowcase.net GOING IN CIRCLES MUSIC: Going In Circles by The Friends Of Distinction (CD: Best Of). Available at iTunes, Amazon.com, Amazon.co.uk, Amazon.de. Also try versions by Luther Vandross and The Gap Band. SEQUENCE: 48 count intro, begin on vocals. 9 count tag after 2nd and 6th repetitions; restart 4th repetition after 24 counts* (you’ll be facing 12:00 when these happen). L TWINKLE, 1/2 TURN R TWINKLE 1,2,3 Cross, side, close (Begin facing 1:30) Step L forward across R (1), Step R side right angling body left COUNTS (to 11:30) (2), Step L beside R (3) 48/2 4,5,6 Cross, turn half Step R across L (4), Turn 1/8 right (3:00) stepping L back (5), Turn 3/8 right (6:00) stepping R side right (6) LEVEL SLOW 1/2 PIVOT, CROSS, R SIDE LUNGE INT 1,2,3 Slow half turn Step L forward toward 7:30 (1), Slowly rotate 1/2 turn right (1:30), taking weight R (2-3) 4,5,6 Cross, lunge right Step L forward across R (4), Squaring up to 12:00, press R side right bending knee/ lowering body into lunge (5-6) Styling for 4-6: Hands palms down or raise right arm overhead clockwise. 1 1/4 ROLLING TURN LEFT, SLOW 1/4 PIVOT 1,2,3 1/4, 1/2, 1/2 (Straighten body) Turn 1/4 left (9:00) stepping L forward (1), Turn 1/2 left (3:00) stepping R back (2), Turn 1/2 left (9:00) stepping L forward (3) 4,5,6 Slow 1/4 left Step R forward (4), Slowly turn 1/4 left taking weight L (6:00) (5-6) WEAVE LEFT, L SIDE, R DRAG, R STEP 1,2,3 Cross, side, behind Step R across L (1), Step L side left (2), Step R behind L (3) 4,5,6 Side, drag, step Big L step side -
Going Round in Circles 220813
s The consumer experience of dealing with problems with communications services 1 Legal notice © 2013 Ipsos MORI – all rights reserved. The contents of this report constitute the sole and exclusive property of Ipsos MORI. Ipsos MORI retains all right, title and interest, including without limitation copyright, in or to any Ipsos MORI trademarks, technologies, methodologies, products, analyses, software and know-how included or arising out of this report or used in connection with the preparation of this report. No license under any copyright is hereby granted or implied. 2 Contents Research highlights ....................................................... 4 Introduction .............................................................. 11 1. Why people don’t make contact .................................. 15 2. Why people do make contact ...................................... 23 3. The contact experience ............................................ 31 4. Why people give up ................................................. 39 5. Resolution ............................................................. 47 6. Escalation and compensation ...................................... 53 7. The influence of personal characteristics ...................... 58 3 Research highlights This qualitative research project investigated why some customers who had cause to contact their suppliers about a communications service issue did not do so, and explores the experiences of those customers who did contact their service providers. Sixty in-depth interviews, each -
![Shape up [Pdf]](https://docslib.b-cdn.net/cover/9491/shape-up-pdf-6519491.webp)
Shape up [Pdf]
Ryan Singer Shape Up Stop Running in Circles and Ship Work that Matters Contents Foreword by Jason Fried 8 Acknowledgements 10 Introduction 11 Growing pains 11 Six-week cycles 14 Shaping the work 14 Making teams responsible 15 Targeting risk 15 How this book is organized 16 Part 1: Shaping Principles of Shaping 20 Wireframes are too concrete 20 Words are too abstract 21 Case study: The Dot Grid Calendar 21 Property 1: It’s rough 24 Property 2: It’s solved 25 Property 3: It’s bounded 25 Who shapes 25 Two tracks 26 Steps to shaping 27 Set Boundaries 28 Setting the appetite 28 Fixed time, variable scope 29 “Good” is relative 30 Responding to raw ideas 31 Narrow down the problem 31 Case study: Defining “calendar” 32 Watch out for grab-bags 33 Boundaries in place 34 Find the Elements 35 Move at the right speed 35 Breadboarding 36 Fat marker sketches 41 Elements are the output 44 Room for designers 46 Not deliverable yet 46 No conveyor belt 47 Risks and Rabbit Holes 48 Different categories of risk 49 Look for rabbit holes 50 Case study: Patching a hole 51 Declare out of bounds 53 Cut back 54 Present to technical experts 54 De-risked and ready to write up 56 Write the Pitch 57 Ingredient 1. Problem 58 Ingredient 2. Appetite 59 Ingredient 3. Solution 60 Help them see it 60 Embedded Sketches 61 Annotated fat marker sketches 62 Ingredient 4. Rabbit holes 64 Ingredient 5. No Gos 64 Examples 64 Ready to present 67 How we do it in Basecamp 67 Part 2: Betting Bets, Not Backlogs 72 No backlogs 72 A few potential bets 73 Decentralized lists 73 Important -
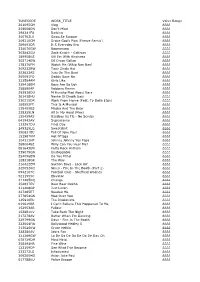
TUNECODE WORK TITLE Value Range 261095CM
TUNECODE WORK_TITLE Value Range 261095CM Vlog ££££ 259008DN Don't Mind ££££ 298241FU Barking ££££ 300703LV Swag Se Swagat ££££ 309210CM Drake God's Plan (Freeze Remix) ££££ 289693DR It S Everyday Bro ££££ 234070GW Boomerang ££££ 302842GU Zack Knight - Galtiyan ££££ 189958KS Kill Em With Kindness ££££ 302714EW Dil Diyan Gallan ££££ 178176FM Watch Me (Whip Nae Nae) ££££ 309232BW Tiger Zinda Hai ££££ 253823AS Juju On The Beat ££££ 265091FQ Daddy Says No ££££ 232584AM Girls Like ££££ 329418BM Boys Are So Ugh ££££ 258890AP Robbery Remix ££££ 292938DU M Huncho Mad About Bars ££££ 261438HU Nashe Si Chadh Gayi ££££ 230215DR Work From Home (Feat. Ty Dolla $Ign) ££££ 188552FT This Is A Musical ££££ 135455BS Masha And The Bear ££££ 238329LN All In My Head (Flex) ££££ 155459AS Bassboy Vs Tlc - No Scrubs ££££ 041942AV Supernanny ££££ 133267DU Final Day ££££ 249325LQ Sweatshirt ££££ 290631EU Fall Of Jake Paul ££££ 153987KM Hot N*Gga ££££ 304111HP Johnny Johnny Yes Papa ££££ 2680048Z Willy Can You Hear Me? ££££ 081643EN Party Rock Anthem ££££ 239079GN Unstoppable ££££ 254096EW Do You Mind ££££ 128318GR The Way ££££ 216422EM Section Boyz - Lock Arf ££££ 325052KQ Nines - Fire In The Booth (Part 2) ££££ 0942107C Football Club - Sheffield Wednes ££££ 5211555C Elevator ££££ 311205DQ Change ££££ 254637EV Baar Baar Dekho ££££ 311408GP Just Listen ££££ 227485ET Needed Me ££££ 277854GN Mad Over You ££££ 125910EU The Illusionists ££££ 019619BR I Can't Believe This Happened To Me ££££ 152953AR Fallout ££££ 153881KV Take Back The Night ££££ 217278AV Better When -

Oral History Interview with Ted Halkin, 2015 July 29- August 17
Oral history interview with Ted Halkin, 2015 July 29- August 17 Funding for this interview was provided by the Terra Foundation for American Art. Contact Information Reference Department Archives of American Art Smithsonian Institution Washington. D.C. 20560 www.aaa.si.edu/askus Transcript Preface The following oral history transcript is the result of a recorded interview with Theodore (Ted) Halkin on 2015 July 29 and August 17. The interview took place at Halkin's home in Evanston, Ill. and was conducted by Lanny Silverman for the Archives of American Art, Smithsonian Institution. This interview is part of the Archives of American Art's Chicago Art and Artists: Oral History Project. Theodore Halkin and Sylvia Halkin, his daughter, have reviewed the transcript. Their corrections and emendations appear below in brackets with initials. This transcript has been lightly edited for readability by the Archives of American Art. The reader should bear in mind that they are reading a transcript of spoken, rather than written, prose. Interview LANNY SILVERMAN: Hello, it's been a while. This is Lanny Silverman for the Smithsonian Institution's Archives of American Art. I'm here at Theodore Halkin's house. It's July 29th, and this is part one of an interview. That looks pretty good. [END OF halkin15_1of2_sd_track01.] LANNY SILVERMAN: I think recording levels look pretty good, down a little. So, I guess the first question, we'll start—the idea of this is to possibly go in chronological order. Although I found with Evelyn and some people they go in circles [laughs], Vera Klement.