A Non Linear Multifractal Study to Illustrate the Evolution of Tagore Songs Over a Century
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rabindra Sangeet
UNIVERSITY GRANTS COMMISSION NET BUREAU Subject: MUSIC Code No.: 16 SYLLABUS Hindustani (Vocal, Instrumental & Musicology), Karnataka, Percussion and Rabindra Sangeet Note:- Unit-I, II, III & IV are common to all in music Unit-V to X are subject specific in music www.careerindia.com -1- Unit-I Technical Terms: Sangeet, Nada: ahata & anahata , Shruti & its five jaties, Seven Vedic Swaras, Seven Swaras used in Gandharva, Suddha & Vikrit Swara, Vadi- Samvadi, Anuvadi-Vivadi, Saptak, Aroha, Avaroha, Pakad / vishesa sanchara, Purvanga, Uttaranga, Audava, Shadava, Sampoorna, Varna, Alankara, Alapa, Tana, Gamaka, Alpatva-Bahutva, Graha, Ansha, Nyasa, Apanyas, Avirbhav,Tirobhava, Geeta; Gandharva, Gana, Marga Sangeeta, Deshi Sangeeta, Kutapa, Vrinda, Vaggeyakara Mela, Thata, Raga, Upanga ,Bhashanga ,Meend, Khatka, Murki, Soot, Gat, Jod, Jhala, Ghaseet, Baj, Harmony and Melody, Tala, laya and different layakari, common talas in Hindustani music, Sapta Talas and 35 Talas, Taladasa pranas, Yati, Theka, Matra, Vibhag, Tali, Khali, Quida, Peshkar, Uthaan, Gat, Paran, Rela, Tihai, Chakradar, Laggi, Ladi, Marga-Deshi Tala, Avartana, Sama, Vishama, Atita, Anagata, Dasvidha Gamakas, Panchdasa Gamakas ,Katapayadi scheme, Names of 12 Chakras, Twelve Swarasthanas, Niraval, Sangati, Mudra, Shadangas , Alapana, Tanam, Kaku, Akarmatrik notations. Unit-II Folk Music Origin, evolution and classification of Indian folk song / music. Characteristics of folk music. Detailed study of folk music, folk instruments and performers of various regions in India. Ragas and Talas used in folk music Folk fairs & festivals in India. www.careerindia.com -2- Unit-III Rasa and Aesthetics: Rasa, Principles of Rasa according to Bharata and others. Rasa nishpatti and its application to Indian Classical Music. Bhava and Rasa Rasa in relation to swara, laya, tala, chhanda and lyrics. -

School of Cultural Texts and Records, Jadavpur University)
4.2. SELF APPRAISAL REPORT ON DOCUMENTATION OF CULTURAL TEXTS (SCHOOL OF CULTURAL TEXTS AND RECORDS, JADAVPUR UNIVERSITY) 4.2.1 Contributing Faculty Members (PI/direct supervision of research projects) 1. PROFESSOR AMLAN DAS GUPTA, PROFESSOR OF ENGLISH Digitization of Cultural Material Digital Music Archiving Electronic Editing 2. DR ABHIJIT GUPTA, ASSOCIATE PROFESSOR OF ENGLISH Early Bengali Books Location Register Physical Culture in Bengal 3. SHRI RAJESWAR SINHA, ASST. PROFESSOR OF BENGALI Travel Literature in Bengal Database Advisory Faculty 1. PROFESSOR SUKANTA CHAUDHURI (PROFESSOR EMERITUS, JADAVPUR UNIVERSITY) 2. PROFESSOR SUPRIYA CHAUDHURI (PROFESSOR EMERITA, JADAVPUR UNIVERSITY) 3. PROFESSOR SWAPAN CHAKRAVORTY, PROFESSOR OF ENGLISH 4. PROFESSOR MOINAK BISWAS, PROFESSOR OF FILM STUDIES 5. PROFESSOR SAMANTAK DAS, ASSOCIATE PROFESSOR OF COMPARATIVE LITERATURE 6. DR RIMI B CHATTERJEE, ASSOCIATE PROFESSOR OF ENGLISH Project Staff under UPE 2 as on 1 January 2014 1. Sri Subrata Sinha, Research Fellow 2. Dr Spandana Bhowmik, Research Fellow 3. Dr Debapriya Basu, Research Fellow 4. Dr Sudeshna Datta Chaudhuri Basu, Project Fellow 5. Ms Purbasha Auddy, Project Fellow 6. Dr Deeptanil Roy, Project Fellow 7. Sri Nikhilesh Bhattacharya, Project Fellow 8. Ms Moumita Haldar, Project Fellow 9. Ms Asmita Chaudhuri, Project Fellow 4.2.2 Relevant Projects in Last 10 years including the Ongoing Projects (MAJOR PROJECTS ONLY) Project Title Sponsoring Members Grant Value Duration Agency (Rs in Lakh) DOCUMENTATION OF UGC ‐ UPE 1 SUKANTA CHAUDHURI, -

Tomar Holo Shuru Amar Holo Shara-Free Download
Tomar holo shuru amar holo shara-free download LINK TO DOWNLOAD 18/08/ · Tomar Holo Shuru Amar Holo Sara Rabindra Sangeet Movies Preview DOWNLOAD OPTIONS download 1 file. MPEG4 download. download 1 file. OGG VIDEO download. download 1 file. TORRENT download. download 13 Files download 5 Original. SHOW ALL. IN COLLECTIONS. Listen to Tomar Holo Shuru Amar Holo Sara on the Bengali music album Jontre Rabindranath Togore by Violin Brothers, only on JioSaavn. Play online or download to listen offline free - . Tomar Holo Shuru Amar Holo Sara Song: Download Tomar Holo Shuru Amar Holo Sara mp3 song from Chayanika. Listen Tomar Holo Shuru Amar Holo Sara mp3 songs free online by Hemanta Mukherjee,Lata Mangeshkar. Download Tomar Holo Shuru Amar Holo Sara on Hungama Music app & get access to Chayanika unlimited free songs, free movies, latest music videos, online radio, new TV . Hemanta - Tomar Holo Shuru Amar Holo Shara - Bangla Song Download. Bangla Music, Bangla MP3, Bangla Song. Listen to Tomar Holo Shuru Amar Holo Sara Piano on the Bengali music album The Piano Sings Rabindra Sangeet by Y. S. Moolky, only on JioSaavn. Play online or download to listen offline free - in HD audio, only on JioSaavn. Tomar Holo Shuru Songs Download- Listen Bengali Tomar Holo Shuru MP3 songs online free. Play Tomar Holo Shuru Bengali movie songs MP3 by Dipankar Chattopadhyay and download Tomar Holo Shuru songs on renuzap.podarokideal.ru Tomar Holo Shuru Songs - Download Tomar Holo Shuru mp3 songs to your Hungama account. Get the complete list of Tomar Holo Shuru mp3 songs free online. Find the best place to Tomar Holo Shuru movie songs download list. -

List of Empanelled Artist
INDIAN COUNCIL FOR CULTURAL RELATIONS EMPANELMENT ARTISTS S.No. Name of Artist/Group State Date of Genre Contact Details Year of Current Last Cooling off Social Media Presence Birth Empanelment Category/ Sponsorsred Over Level by ICCR Yes/No 1 Ananda Shankar Jayant Telangana 27-09-1961 Bharatanatyam Tel: +91-40-23548384 2007 Outstanding Yes https://www.youtube.com/watch?v=vwH8YJH4iVY Cell: +91-9848016039 September 2004- https://www.youtube.com/watch?v=Vrts4yX0NOQ [email protected] San Jose, Panama, https://www.youtube.com/watch?v=YDwKHb4F4tk [email protected] Tegucigalpa, https://www.youtube.com/watch?v=SIh4lOqFa7o Guatemala City, https://www.youtube.com/watch?v=MiOhl5brqYc Quito & Argentina https://www.youtube.com/watch?v=COv7medCkW8 2 Bali Vyjayantimala Tamilnadu 13-08-1936 Bharatanatyam Tel: +91-44-24993433 Outstanding No Yes https://www.youtube.com/watch?v=wbT7vkbpkx4 +91-44-24992667 https://www.youtube.com/watch?v=zKvILzX5mX4 [email protected] https://www.youtube.com/watch?v=kyQAisJKlVs https://www.youtube.com/watch?v=q6S7GLiZtYQ https://www.youtube.com/watch?v=WBPKiWdEtHI 3 Sucheta Bhide Maharashtra 06-12-1948 Bharatanatyam Cell: +91-8605953615 Outstanding 24 June – 18 July, Yes https://www.youtube.com/watch?v=WTj_D-q-oGM suchetachapekar@hotmail 2015 Brazil (TG) https://www.youtube.com/watch?v=UOhzx_npilY .com https://www.youtube.com/watch?v=SgXsRIOFIQ0 https://www.youtube.com/watch?v=lSepFLNVelI 4 C.V.Chandershekar Tamilnadu 12-05-1935 Bharatanatyam Tel: +91-44- 24522797 1998 Outstanding 13 – 17 July 2017- No https://www.youtube.com/watch?v=Ec4OrzIwnWQ -

2012-01-17 23:39:27 UTC+05:30 1. Name the Rashtriya Lok Dal (RLD) Leader Who Was Inducted Into the Union Cabinet As Civil Aviation Minister on 18 December 2011
CURRENT AFFAIRS MCQs FOR APPSC EXAMS Posted: 2012-01-17 23:39:27 UTC+05:30 1. Name the Rashtriya Lok Dal (RLD) leader who was inducted into the Union Cabinet as civil aviation minister on 18 December 2011. a. Ajit Singh b. Jayant Chaudhary c. Devendra Nagpal d. Sanjay Singh Chauhan Answer: (a) 2. Popularly known as Adam Gondvi, this Hindi poet who wrote revolutionary poetry focusing on the pathetic state of dalits and the poor breathed his last in Lucknow on 18 December 2011. Name the poet. a. Bharat Bhusan b. Ram Nath Singh c. Uday Prakash d. Shail Chaturvedi e. Naresh Mehta Answer: (b) 3. Which world renowned architect was bestowed with Goa's highest civilian honour, the Gomant Vibhushan, on the eve of the Golden Jubiliee of Goa's Liberation on 18 December 2011? a. Michael Hopkins b. Kengo Kuma c. Charles Correa d. Kevin Kennon Answer: (c) 4. The Union cabinet of India on 22 December 2011 approved __ percent share for minorities within the 27% OBC quota in jobs and university seats. a) 4.5 b) 5.6 c) 3.4 d) 5 Answer: (a) 4.5 5. The Manipur Legislative Assembly passed the Manipur Lokayukta Bill, 2011. Manipur will be the __state in North-Eastern India to have alegislation of Lokayukta. a) Second b) Third c) First d) Fourth Answer: (b) Third 6. Oman Investment Fund (OIF), the Sultanate of Oman’s sovereign wealth fund, filed application with the government to buy a stake in which of the software solutions company, IT People promoted exchange? a. -
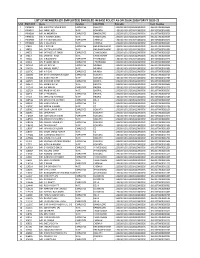
LIST of MEMBERS (EX-EMPLOYEES) ENROLLED in BASE POLICY AS on 20.04.2020 for FY 2020-21 S.NO EMPCODE Name Relation LOCATION Policyno Card Number 1 PRMB22 MR
LIST OF MEMBERS (EX-EMPLOYEES) ENROLLED IN BASE POLICY AS ON 20.04.2020 FOR FY 2020-21 S.NO EMPCODE Name Relation LOCATION PolicyNo Card_Number 1 PRMB22 MR. SWAPAN KUMAR ROY EMPLOYEE KOLKATA :130200/130132028120000030 :0611070000283626 2 PRMB22 MS. DIPALI ROY WIFE KOLKATA :130200/130132028120000030 :0611070000283603 3 PRMB19 MR. M AKBARSHA EMPLOYEE BANGALORE :130200/130132028120000030 :0611070000283526 4 PRMB19 MS. A HAMIDA BANU WIFE BANGALORE :130200/130132028120000030 :0611070000283503 5 PRMB09 MR. T S VIJAYAKUMAR EMPLOYEE CHENNAI :130200/130132028120000030 :0611070000283426 6 PRMB09 MS. V KALAIVANI WIFE CHENNAI :130200/130132028120000030 :0611070000283403 7 14819J MR. P N PATRI EMPLOYEE BHUBANESHWAR :130200/130132028120000030 :0611070000283326 8 14819J MS. GEETANJALI PATRI WIFE BHUBANESHWAR :130200/130132028120000030 :0611070000283303 9 14027J MR. JATINDERJIT SINGH EMPLOYEE CHANDIGARH :130200/130132028120000030 :0611070000283226 10 14027J MS. JASWANT KAUR WIFE CHANDIGARH :130200/130132028120000030 :0611070000283203 11 13346J MS. D RAMADEVI EMPLOYEE HYDERABAD :130200/130132028120000030 :0611070000283126 12 13314L MS. P SABIRUNNISA EMPLOYEE HYDERABAD :130200/130132028120000030 :0611070000283026 13 12435D MR. H C RAJPUT EMPLOYEE MUMBAI :130200/130132028120000030 :0611070000282926 14 12435D MS. MANJU RAJPUT WIFE MUMBAI :130200/130132028120000030 :0611070000282903 15 12363C MR. N R DAS EMPLOYEE MUMBAI :130200/130132028120000030 :0611070000282826 16 12358G MR. BHIM CHANDRA HALDER EMPLOYEE KOLKATA :130200/130132028120000030 :0611070000282726 -

MUSIC Hindustani
The Maharaja Sayajirao University of Baroda, Vadodara Ph. D Entrance Tet (PET) SYLLABUS Subject: MUSIC PET ExamCode : 21 Hindustani (Vocal, Instrumental & Musicology), Karnataka, Percussion and Rabindra Sangeet Note:- Unit-I, II, III & IV are common to all in music Unit-V to X are subject specific in music -1- Unit-I Technical Terms: Sangeet, Nada: ahata & anahata , Shruti & its five jaties, Seven Vedic Swaras, Seven Swaras used in Gandharva, Suddha & Vikrit Swara, Vadi- Samvadi, Anuvadi-Vivadi, Saptak, Aroha, Avaroha, Pakad / vishesa sanchara, Purvanga, Uttaranga, Audava, Shadava, Sampoorna, Varna, Alankara, Alapa, Tana, Gamaka, Alpatva-Bahutva, Graha, Ansha, Nyasa, Apanyas, Avirbhav,Tirobhava, Geeta; Gandharva, Gana, Marga Sangeeta, Deshi Sangeeta, Kutapa, Vrinda, Vaggeyakara Mela, Thata, Raga, Upanga ,Bhashanga ,Meend, Khatka, Murki, Soot, Gat, Jod, Jhala, Ghaseet, Baj, Harmony and Melody, Tala, laya and different layakari, common talas in Hindustani music, Sapta Talas and 35 Talas, Taladasa pranas, Yati, Theka, Matra, Vibhag, Tali, Khali, Quida, Peshkar, Uthaan, Gat, Paran, Rela, Tihai, Chakradar, Laggi, Ladi, Marga-Deshi Tala, Avartana, Sama, Vishama, Atita, Anagata, Dasvidha Gamakas, Panchdasa Gamakas ,Katapayadi scheme, Names of 12 Chakras, Twelve Swarasthanas, Niraval, Sangati, Mudra, Shadangas , Alapana, Tanam, Kaku, Akarmatrik notations. Unit-II Folk Music Origin, evolution and classification of Indian folk song / music. Characteristics of folk music. Detailed study of folk music, folk instruments and performers of various regions in India. Ragas and Talas used in folk music Folk fairs & festivals in India. -2- Unit-III Rasa and Aesthetics: Rasa, Principles of Rasa according to Bharata and others. Rasa nishpatti and its application to Indian Classical Music. Bhava and Rasa Rasa in relation to swara, laya, tala, chhanda and lyrics. -

Sankeet Natak Akademy Awards from 1952 to 2016
All Sankeet Natak Akademy Awards from 1952 to 2016 Yea Sub Artist Name Field Category r Category Prabhakar Karekar - 201 Music Hindustani Vocal Akademi 6 Awardee Padma Talwalkar - 201 Music Hindustani Vocal Akademi 6 Awardee Koushik Aithal - 201 Music Hindustani Vocal Yuva Puraskar 6 Yashasvi 201 Sirpotkar - Yuva Music Hindustani Vocal 6 Puraskar Arvind Mulgaonkar - 201 Music Hindustani Tabla Akademi 6 Awardee Yashwant 201 Vaishnav - Yuva Music Hindustani Tabla 6 Puraskar Arvind Parikh - 201 Music Hindustani Sitar Akademi Fellow 6 Abir hussain - 201 Music Hindustani Sarod Yuva Puraskar 6 Kala Ramnath - 201 Akademi Music Hindustani Violin 6 Awardee R. Vedavalli - 201 Music Carnatic Vocal Akademi Fellow 6 K. Omanakutty - 201 Akademi Music Carnatic Vocal 6 Awardee Neela Ramgopal - 201 Akademi Music Carnatic Vocal 6 Awardee Srikrishna Mohan & Ram Mohan 201 (Joint Award) Music Carnatic Vocal 6 (Trichur Brothers) - Yuva Puraskar Ashwin Anand - 201 Music Carnatic Veena Yuva Puraskar 6 Mysore M Manjunath - 201 Music Carnatic Violin Akademi 6 Awardee J. Vaidyanathan - 201 Akademi Music Carnatic Mridangam 6 Awardee Sai Giridhar - 201 Akademi Music Carnatic Mridangam 6 Awardee B Shree Sundar 201 Kumar - Yuva Music Carnatic Kanjeera 6 Puraskar Ningthoujam Nata Shyamchand 201 Other Major Music Sankirtana Singh - Akademi 6 Traditions of Music of Manipur Awardee Ahmed Hussain & Mohd. Hussain (Joint Award) 201 Other Major Sugam (Hussain Music 6 Traditions of Music Sangeet Brothers) - Akademi Awardee Ratnamala Prakash - 201 Other Major Sugam Music Akademi -

Macron Vows to Heal After Divisive Campaign
millenniumpost.in RNI NO.: WBENG/2015/65962 PUBLISHED FROM DELHI & KOLKATA VOL. 3, ISSUE 124 | Tuesday, 9 May 2017 | Kolkata | Pages 16 | Rs 3.00 NO HALF TRUTHS pNIFTY 9314.05 (-28.75) pSENSEX 29,926.15 (-67.35) qDOW JONES 20,975.81 (-31.13) qNASDAQ 6,093.73 (-7.03) pRUPEE/DOLLAR 64.31 (+0.07) qRUPEE/EURO 70.40 (+0.33) qGOLD/10GM 28,550.00 (-175.00) qSILVER/K 38,350.00 (--225.00) TOUGHER BENGALI MP RIOTS OVER COW: 11 MIGRANTS DEAD, NEVER READ A NEET PAPER: MAMATA SC PULLS UP POLICE 200 MISSING IN CHETAN BHAGAT ‘HURT’, STATE TO FOR NOT EXAMINING MEDITERRANEAN BOOK: ARJUN WRITE TO CENTRE’ PG3 VIDEOS PG7 SINKINGS PG11 KAPOOR PG16 SC BLOW FOR LALU YOUNGEST EVER FRENCH PRESIDENT Rajnath calls for ‘unity of Bihar Grand Alliance will remain intact: JD(U) Macron vows to heal purpose’ to tackle Naxals DHIRENDRA KUMAR MPOST BUREAU vehicles (UAVs) would be pressed into service NEW DELHI: The Supreme Court’s verdict NEW DELHI: Calling to bust their hideouts. to revive conspiracy charges against Rashtriya for “unity of purpose” “I am sure that the Janata Dal (RJD) supremo Lalu Prasad Yadav after divisive campaign amongst all Naxal- attempts to stall devel- and others in multi-crore fodder scam cases will affected states, Union opment and throttle not create any political crisis in Bihar, political PARIS: Pro-European centrist gramme has been defeated. Home Minister Rajnath democracy at gunpoint experts said. Emmanuel Macron promised on I will fight with all my German Chancellor Angela Singh on Monday advocated the will not be successful ever,” the According to them, the Grand Alliance Monday to heal France’s divisions Merkel’s spokesman said it was a formation of a strategic and uni- home minister said at the meet- would remain unscathed as the verdict is part after crushing far- right leader strength against the divisions “victory for a strong and united fied command to foil attempts to ing, being held two weeks after of the ongoing trial of the cases. -
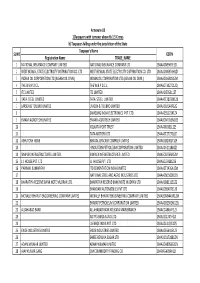
FINAL DISTRIBUTION.Xlsx
Annexure-1B 1)Taxpayers with turnover above Rs 1.5 Crores b) Taxpayers falling under the jurisdiction of the State Taxpayer's Name SL NO GSTIN Registration Name TRADE_NAME 1 NATIONAL INSURANCE COMPANY LIMITED NATIONAL INSURANCE COMPANY LTD 19AAACN9967E1Z0 2 WEST BENGAL STATE ELECTRICITY DISTRIBUTION CO. LTD WEST BENGAL STATE ELECTRICITY DISTRIBUTION CO. LTD 19AAACW6953H1ZX 3 INDIAN OIL CORPORATION LTD.(ASSAM OIL DIVN.) INDIAN OIL CORPORATION LTD.(ASSAM OIL DIVN.) 19AAACI1681G1ZM 4 THE W.B.P.D.C.L. THE W.B.P.D.C.L. 19AABCT3027C1ZQ 5 ITC LIMITED ITC LIMITED 19AAACI5950L1Z7 6 TATA STEEL LIMITED TATA STEEL LIMITED 19AAACT2803M1Z8 7 LARSEN & TOUBRO LIMITED LARSEN & TOUBRO LIMITED 19AAACL0140P1ZG 8 SAMSUNG INDIA ELECTRONICS PVT. LTD. 19AAACS5123K1ZA 9 EMAMI AGROTECH LIMITED EMAMI AGROTECH LIMITED 19AABCN7953M1ZS 10 KOLKATA PORT TRUST 19AAAJK0361L1Z3 11 TATA MOTORS LTD 19AAACT2727Q1ZT 12 ASHUTOSH BOSE BENGAL CRACKER COMPLEX LIMITED 19AAGCB2001F1Z9 13 HINDUSTAN PETROLEUM CORPORATION LIMITED. 19AAACH1118B1Z9 14 SIMPLEX INFRASTRUCTURES LIMITED. SIMPLEX INFRASTRUCTURES LIMITED. 19AAECS0765R1ZM 15 J.J. HOUSE PVT. LTD J.J. HOUSE PVT. LTD 19AABCJ5928J2Z6 16 PARIMAL KUMAR RAY ITD CEMENTATION INDIA LIMITED 19AAACT1426A1ZW 17 NATIONAL STEEL AND AGRO INDUSTRIES LTD 19AAACN1500B1Z9 18 BHARATIYA RESERVE BANK NOTE MUDRAN LTD. BHARATIYA RESERVE BANK NOTE MUDRAN LTD. 19AAACB8111E1Z2 19 BHANDARI AUTOMOBILES PVT LTD 19AABCB5407E1Z0 20 MCNALLY BHARAT ENGGINEERING COMPANY LIMITED MCNALLY BHARAT ENGGINEERING COMPANY LIMITED 19AABCM9443R1ZM 21 BHARAT PETROLEUM CORPORATION LIMITED 19AAACB2902M1ZQ 22 ALLAHABAD BANK ALLAHABAD BANK KOLKATA MAIN BRANCH 19AACCA8464F1ZJ 23 ADITYA BIRLA NUVO LTD. 19AAACI1747H1ZL 24 LAFARGE INDIA PVT. LTD. 19AAACL4159L1Z5 25 EXIDE INDUSTRIES LIMITED EXIDE INDUSTRIES LIMITED 19AAACE6641E1ZS 26 SHREE RENUKA SUGAR LTD. 19AADCS1728B1ZN 27 ADANI WILMAR LIMITED ADANI WILMAR LIMITED 19AABCA8056G1ZM 28 AJAY KUMAR GARG OM COMMODITY TRADING CO. -

Infinitydraftfinal 110712.Pub
2 Editor Mr.Dilip Kumar Sen, Head, Dept. of English Joint Convener - Ms. Leena Sarkar Bhaduri ,Dept. of English Ms. Barnali Goswami, Dept. of CA Member - Mr. Sajal Saha, Dept. of CA Mr. Arindam Chatterjee, Registrar(Acting) Ms.Rumpa Saha, Dept. of EE Dr. Subhasis Biswas, Dept. of Chemistry Dr. Sumit Nandi,Dept. of Chemistry Students - Sourav Majumdar EE2A Arittra Pramanick IT2 Souradeep Sinha EE2A Indranil Samanta IT2 Bhaswati Chatterjee ECE1A Bhaglyalakshmi Mishra IT2 Arsi Chatterjee CSE2A 3 infi NIT y Vol-1 No. 2 May2012 Narula Institute of Technology Achievements Inside this issue: The Other Tagore 3 Department of Computer Application published the inaugural issue “International Journal of Frontier Computing (IJFC)”. The inaugural Tagore Remixed: Moderniza- 5 issue contains 10 high quality peer reviewed paper. tion or Vandalism? Department of Electrical Engineering organized one day workshop on Reflection on Paintings of 7 “Electrical Energy and Future” on 11.02.12 Rabindranath Tagore NIT organized an event on the occasion of 150th birth anniversary of Swami Vivekananda on 25.04.12 lh£¾cÊe¡b J ¢h‘¡e 9 NIT organizes a blood donation camp on 09.02.12 Event 12 JIS Group organizes an inter college cricket tournament where JIS college of engineering, Kalyani won the trophy and Narula institute of Photo ultimo 13 Technology was the runners up. English department organized interdepartmental power point presenta- Sketch 12 tion competition 03.05.12 Department of ECE organized national level workshop “Antenna model- An Initiative of Literary Committee, ing using HFSS and it’s Application” on 22nd-23rd June, 2012. Narula Institute of Technology. -

P壓 闋lp G縴 蛻 瞭i斂p 民獝 S鍊母p髻擬 C瑰繗 母j鬆扚 (P 補m
PÀ£ÁðlPÀ gÁdå ¸ÀºÁAiÀÄPÀ ¥ÁæzsÁå¥ÀPÀgÀÀ CºÀðvÁ ¥ÀjÃPÉë (PÉ-¸Émï) KARNATAKA STATE ELIGIBILITY TEST (K-SET) FOR ASSISTANT PROFESSOR SYLLABUS Subject: MUSIC Subject Code: 40 Unit-I Technical Terms: Sangeet, Nada: ahata & anahata , Shruti & its five jaties, Seven Vedic Swaras, Seven Swaras used in Gandharva, Suddha & Vikrit Swara, Vadi- Samvadi, Anuvadi-Vivadi, Saptak, Aroha, Avaroha, Pakad / vishesa sanchara, Purvanga, Uttaranga, Audava, Shadava, Sampoorna, Varna, Alankara, Alapa, Tana, Gamaka, Alpatva-Bahutva, Graha, Ansha, Nyasa, Apanyas, Avirbhav,Tirobhava, Geeta; Gandharva, Gana, Marga Sangeeta, Deshi Sangeeta, Kutapa, Vrinda, Vaggeyakara Mela, Thata, Raga, Upanga ,Bhashanga ,Meend, Khatka, Murki, Soot, Gat, Jod, Jhala, Ghaseet, Baj, Harmony and Melody, Tala, laya and different layakari, common talas in Hindustani music, Sapta Talas and 35 Talas, Taladasa pranas, Yati, Theka, Matra, Vibhag, Tali, Khali, Quida, Peshkar, Uthaan, Gat, Paran, Rela, Tihai, Chakradar, Laggi, Ladi, Marga- Deshi Tala, Avartana, Sama, Vishama, Atita, Anagata, Dasvidha Gamakas, Panchdasa Gamakas ,Katapayadi scheme, Names of 12 Chakras, Twelve Swarasthanas, Niraval, Sangati, Mudra, Shadangas , Alapana, Tanam, Kaku, Akarmatrik notations. Unit-II Folk Music Origin, evolution and classification of Indian folk song / music. Characteristics of folk music. Detailed study of folk music, folk instruments and performers of various regions in India. Ragas and Talas used in folk music Folk fairs & festivals in India. Unit-III Rasa and Aesthetics: Rasa, Principles of Rasa according to Bharata and others. Rasa nishpatti and its application to Indian Classical Music. Bhava and Rasa Rasa in relation to swara, laya, tala, chhanda and lyrics. Aesthetics according to Indian and western Philosophers. General knowledge of 64 kalas according to Vatsyayan General history of Raga-Ragini Paintings and Raga Dhayana.