6.867 Machine Learning Problem 1: Model Selection
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Propensity Scores up to Head(Propensitymodel) – Modify the Number of Threads! • Inspect the PS Distribution Plot • Inspect the PS Model
Overview of the CohortMethod package Martijn Schuemie CohortMethod is part of the OHDSI Methods Library Cohort Method Self-Controlled Case Series Self-Controlled Cohort IC Temporal Pattern Disc. Case-control New-user cohort studies using Self-Controlled Case Series A self-controlled cohort A self-controlled design, but Case-control studies, large-scale regressions for analysis using fews or many design, where times preceding using temporals patterns matching controlss on age, propensity and outcome predictors, includes splines for exposure is used as control. around other exposures and gender, provider, and visit models age and seasonality. outcomes to correct for time- date. Allows nesting of the Estimation methods varying confounding. study in another cohort. Patient Level Prediction Feature Extraction Build and evaluate predictive Automatically extract large models for users- specified sets of featuress for user- outcomes, using a wide array specified cohorts using data in of machine learning the CDM. Prediction methods algorithms. Empirical Calibration Method Evaluation Use negative control Use real data and established exposure-outcomes pairs to reference sets ass well as profile and calibrate a simulations injected in real particular analysis design. data to evaluate the performance of methods. Method characterization Database Connector Sql Render Cyclops Ohdsi R Tools Connect directly to a wide Generate SQL on the fly for Highly efficient Support tools that didn’t fit range of databases platforms, the various SQLs dialects. implementations of regularized other categories,s including including SQL Server, Oracle, logistic, Poisson and Cox tools for maintaining R and PostgreSQL. regression. libraries. Supporting packages Under construction Technologies CohortMethod uses • DatabaseConnector and SqlRender to interact with the CDM data – SQL Server – Oracle – PostgreSQL – Amazon RedShift – Microsoft APS • ff to work with large data objects • Cyclops for large scale regularized regression Graham study steps 1. -

Generalized Scatter Plots
Generalized scatter plots Daniel A. Keim a Abstract Scatter Plots are one of the most powerful and most widely used b techniques for visual data exploration. A well-known problem is that scatter Ming C. Hao plots often have a high degree of overlap, which may occlude a significant Umeshwar Dayal b portion of the data values shown. In this paper, we propose the general a ized scatter plot technique, which allows an overlap-free representation of Halldor Janetzko and large data sets to fit entirely into the display. The basic idea is to allow the Peter Baka ,* analyst to optimize the degree of overlap and distortion to generate the best possible view. To allow an effective usage, we provide the capability to zoom ' University of Konstanz, Universitaetsstr. 10, smoothly between the traditional and our generalized scatter plots. We iden Konstanz, Germany. tify an optimization function that takes overlap and distortion of the visualiza bHewlett Packard Research Labs, 1501 Page tion into acccount. We evaluate the generalized scatter plots according to this Mill Road, Palo Alto, CA94304, USA. optimization function, and show that there usually exists an optimal compro mise between overlap and distortion . Our generalized scatter plots have been ' Corresponding author. applied successfully to a number of real-world IT services applications, such as server performance monitoring, telephone service usage analysis and financial data, demonstrating the benefits of the generalized scatter plots over tradi tional ones. Keywords: scatter plot; overlapping; distortion; interpolation; smoothing; interactions Introduction Motivation Large amounts of multi-dimensional data occur in many important appli cation domains such as telephone service usage analysis, sales and server performance monitoring. -

Propensity Score Matching with R: Conventional Methods and New Features
812 Review Article Page 1 of 39 Propensity score matching with R: conventional methods and new features Qin-Yu Zhao1#, Jing-Chao Luo2#, Ying Su2, Yi-Jie Zhang2, Guo-Wei Tu2, Zhe Luo3 1College of Engineering and Computer Science, Australian National University, Canberra, ACT, Australia; 2Department of Critical Care Medicine, Zhongshan Hospital, Fudan University, Shanghai, China; 3Department of Critical Care Medicine, Xiamen Branch, Zhongshan Hospital, Fudan University, Xiamen, China Contributions: (I) Conception and design: QY Zhao, JC Luo; (II) Administrative support: GW Tu; (III) Provision of study materials or patients: GW Tu, Z Luo; (IV) Collection and assembly of data: QY Zhao; (V) Data analysis and interpretation: QY Zhao; (VI) Manuscript writing: All authors; (VII) Final approval of manuscript: All authors. #These authors contributed equally to this work. Correspondence to: Guo-Wei Tu. Department of Critical Care Medicine, Zhongshan Hospital, Fudan University, Shanghai 200032, China. Email: [email protected]; Zhe Luo. Department of Critical Care Medicine, Xiamen Branch, Zhongshan Hospital, Fudan University, Xiamen 361015, China. Email: [email protected]. Abstract: It is increasingly important to accurately and comprehensively estimate the effects of particular clinical treatments. Although randomization is the current gold standard, randomized controlled trials (RCTs) are often limited in practice due to ethical and cost issues. Observational studies have also attracted a great deal of attention as, quite often, large historical datasets are available for these kinds of studies. However, observational studies also have their drawbacks, mainly including the systematic differences in baseline covariates, which relate to outcomes between treatment and control groups that can potentially bias results. -
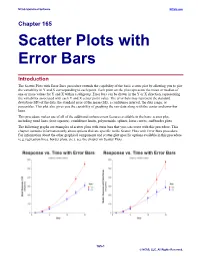
Scatter Plots with Error Bars
NCSS Statistical Software NCSS.com Chapter 165 Scatter Plots with Error Bars Introduction The Scatter Plots with Error Bars procedure extends the capability of the basic scatter plot by allowing you to plot the variability in Y and X corresponding to each point. Each point on the plot represents the mean or median of one or more values for Y and X within a subgroup. Error bars can be drawn in the Y or X direction, representing the variability associated with each Y and X center point value. The error bars may represent the standard deviation (SD) of the data, the standard error of the mean (SE), a confidence interval, the data range, or percentiles. This plot also gives you the capability of graphing the raw data along with the center and error-bar lines. This procedure makes use of all of the additional enhancement features available in the basic scatter plot, including trend lines (least squares), confidence limits, polynomials, splines, loess curves, and border plots. The following graphs are examples of scatter plots with error bars that you can create with this procedure. This chapter contains information only about options that are specific to the Scatter Plots with Error Bars procedure. For information about the other graphical components and scatter-plot specific options available in this procedure (e.g. regression lines, border plots, etc.), see the chapter on Scatter Plots. 165-1 © NCSS, LLC. All Rights Reserved. NCSS Statistical Software NCSS.com Scatter Plots with Error Bars Data Structure This procedure accepts data in four different input formats. The type of plot that can be created depends on the input format. -

Estimation of Average Total Effects in Quasi-Experimental Designs: Nonlinear Constraints in Structural Equation Models
Estimation of Average Total Effects in Quasi-Experimental Designs: Nonlinear Constraints in Structural Equation Models Dissertation zur Erlangung des akademischen Grades doctor philosophiae (Dr. phil.) vorgelegt dem Rat der Fakultät für Sozial- und Verhaltenswissenschaften der Friedrich-Schiller-Universität Jena von Dipl.-Psych. Joachim Ulf Kröhne geboren am 02. Juni 1977 in Jena Gutachter: 1. Prof. Dr. Rolf Steyer (Friedrich-Schiller-Universität Jena) 2. PD Dr. Matthias Reitzle (Friedrich-Schiller-Universität Jena) Tag des Kolloquiums: 23. August 2010 Dedicated to Cora and our family(ies) Zusammenfassung Diese Arbeit untersucht die Schätzung durchschnittlicher totaler Effekte zum Vergleich der Wirksam- keit von Behandlungen basierend auf quasi-experimentellen Designs. Dazu wird eine generalisierte Ko- varianzanalyse zur Ermittlung kausaler Effekte auf Basis einer flexiblen Parametrisierung der Kovariaten- Treatment Regression betrachtet. Ausgangspunkt für die Entwicklung der generalisierten Kovarianzanalyse bildet die allgemeine Theo- rie kausaler Effekte (Steyer, Partchev, Kröhne, Nagengast, & Fiege, in Druck). In dieser allgemeinen Theorie werden verschiedene kausale Effekte definiert und notwendige Annahmen zu ihrer Identifikation in nicht- randomisierten, quasi-experimentellen Designs eingeführt. Anhand eines empirischen Beispiels wird die generalisierte Kovarianzanalyse zu alternativen Adjustierungsverfahren in Beziehung gesetzt und insbeson- dere mit den Propensity Score basierten Analysetechniken verglichen. Es wird dargestellt, -

Algebra 1 Regular/Honors – Phase 2 Part 1 TEXTBOOK CHECKOUT
Algebra 1 Phase 2 – Part 1 Directions: In the pack you will find completed notes with blank TRY IT! and BEAT THE TEST! questions. Read, study, and work through these problems. Focus on trying to do the TRY IT! and BEAT THE TEST! problem to assess your understanding before checking the answers provided at PHASE 2 INSTRUCTIONAL CONTINUITY PLAN the end of the packet. Also included are Independent Practice questions. Complete these and return to your BEGINNING APRIL 16, 2020 teacher/school at a later date. Later, you may be expected to complete the TEST YOURSELF! problems online. (Topic Number 1H after Topic 9 is HONORS ONLY) Topic Date Topic Name Number Completed 9-1 Dot Plots Algebra 1 Regular/Honors – Phase 2 Part 1 9-2 Histograms 9-3 Box Plots – Part 1 TEXTBOOK CHECKOUT: No Textbook Needed 9-4 Box Plots – Part 2 Measures of Center and 9-5 Shapes of Distributions 9-6 Measures of Spread – Part 1 SCHOOL NAME: _____________________ 9-7 Measures of Spread – Part 2 STUDENT NAME: _____________________ 9-8 The Empirical Rule 9-9 Outliers in Data Sets TEACHER NAME: _____________________ 9-1H Normal Distribution 1 What are some things you learned from these sections? Topic Date Topic Name Number Completed Relationship between Two Categorical Variables – Marginal 10-1 and Joint Relative Frequency – Part 1 Relationship between Two Categorical Variables – Marginal 10-2 and Joint Relative Frequency – Part 2 Relationship between Two 10-3 Categorical Variables – Conditional What questions do you still have after studying these Relative Frequency sections? 10-4 Scatter Plot and Function Models 10-5 Residuals and Residual Plots – Part 1 10-6 Residuals and Residual Plots – Part 2 10-7 Examining Correlation 2 Section 9: One-Variable Statistics Section 9 – Topic 1 Dot Plots Statistics is the science of collecting, organizing, and analyzing data. -

Exploring Spatial Data with Geoda: a Workbook
Exploring Spatial Data with GeoDaTM : A Workbook Luc Anselin Spatial Analysis Laboratory Department of Geography University of Illinois, Urbana-Champaign Urbana, IL 61801 http://sal.uiuc.edu/ Center for Spatially Integrated Social Science http://www.csiss.org/ Revised Version, March 6, 2005 Copyright c 2004-2005 Luc Anselin, All Rights Reserved Contents Preface xvi 1 Getting Started with GeoDa 1 1.1 Objectives . 1 1.2 Starting a Project . 1 1.3 User Interface . 3 1.4 Practice . 5 2 Creating a Choropleth Map 6 2.1 Objectives . 6 2.2 Quantile Map . 6 2.3 Selecting and Linking Observations in the Map . 10 2.4 Practice . 11 3 Basic Table Operations 13 3.1 Objectives . 13 3.2 Navigating the Data Table . 13 3.3 Table Sorting and Selecting . 14 3.3.1 Queries . 16 3.4 Table Calculations . 17 3.5 Practice . 20 4 Creating a Point Shape File 22 4.1 Objectives . 22 4.2 Point Input File Format . 22 4.3 Converting Text Input to a Point Shape File . 24 4.4 Practice . 25 i 5 Creating a Polygon Shape File 26 5.1 Objectives . 26 5.2 Boundary File Input Format . 26 5.3 Creating a Polygon Shape File for the Base Map . 28 5.4 Joining a Data Table to the Base Map . 29 5.5 Creating a Regular Grid Polygon Shape File . 31 5.6 Practice . 34 6 Spatial Data Manipulation 36 6.1 Objectives . 36 6.2 Creating a Point Shape File Containing Centroid Coordinates 37 6.2.1 Adding Centroid Coordinates to the Data Table . -

HW: Scatter Plots
HW: Scatter Plots Name: Date: 1. The scatter plot below shows the average traffic 2. Ms. Ochoa recorded the age and shoe size of each volume and average vehicle speed on a certain student in her physical education class. The graph freeway for 50 days in 1999. below shows her data. Which of the following statements about the graph Which statement best describes the relationship is true? between average traffic volume and average vehicle speed shown on the scatter plot? A. The graph shows a positive trend. A. As traffic volume increases, vehicle speed B. The graph shows a negative trend. increases. C. The graph shows a constant trend. B. As traffic volume increases, vehicle speed decreases. D. The graph shows no trend. C. As traffic volume increases, vehicle speed increases at first, then decreases. D. As traffic volume increases, vehicle speed decreases at first, then increases. page 1 3. Which graph best shows a positive correlation 4. Use the scatter plot below to answer the following between the number of hours studied and the test question. scores? A. B. The police department tracked the number of ticket writers and number of tickets issued for the past 8 weeks. The scatter plot shows the results. Based on the scatter plot, which statement is true? A. More ticket writers results in fewer tickets issued. B. There were 50 tickets issued every week. C. When there are 10 ticket writers, there will be 800 tickets issued. C. D. More ticket writers results in more tickets issued. D. page 2 HW: Scatter Plots 5. -

Generalized Sensitivity Analysis and Application to Quasi-Experiments∗
Generalized Sensitivity Analysis and Application to Quasi-experiments∗ Masataka Harada New York University [email protected] August 27, 2013 Abstract The generalized sensitivity analysis (GSA) is a sensitivity analysis for unobserved confounders characterized by a computational approach with dual sensitivity parame- ters. Specifically, GSA generates an unobserved confounder from the residuals in the outcome and treatment models, and random noise to estimate the confounding effects. GSA can deal with various link functions and identify necessary confounding effects with respect to test-statistics while minimizing the changes to researchers’ original es- timation models. This paper first provides a brief introduction of GSA comparing its relative strength and weakness. Then, its versatility and simplicity of use are demon- strated through its applications to the studies that use quasi-experimental methods, namely fixed effects, propensity score matching, and instrumental variable. These ap- plications provide new insights as to whether and how our statistical inference gains robustness to unobserved confounding by using quasi-experimental methods. ∗I thank Christopher Berry, Jennifer Hill, Luke Keele, Robert LaLonde, Andrew Martin, Marc Scott, Teppei Yamamoto for helpful comments on earlier drafts of this paper. 1 Introduction Political science research nowadays commands a wide variety of quasi-experimental tech- niques intended to help identify causal effects.1 Researchers often begin with collecting extensive panel data to control for unit heterogeneities with difference in differences or fixed effects. When panel data are not available or the key explanatory variable has no within- unit variation, researchers typically match treated units with control units from a multitude of matching techniques. Perhaps, they are fortunate to find a good instrumental variable which is effectively randomly assigned and affects the outcome only through the treatment variable. -

On Assessing the Specification of Propensity Score Models
On Assessing the Specification of Propensity Score Models Wang-Sheng Lee* Melbourne Institute of Applied Economic and Social Research The University of Melbourne May 18, 2007 Abstract This paper discusses a graphical method and a closely related regression test for assessing the specification of the propensity score, an area which the literature currently offers little guidance. Based on a Monte Carlo study, it is found that the proposed regression test has power to detect a misspecified propensity score in the case when the propensity score model is under-specified (i.e., needs higher order terms or interactions) as well as in the case when a relevant covariate is inadvertently excluded. In light of findings in the recent literature that suggest that there appears to be little penalty to over-specifying the propensity score, a possible strategy for applied researchers would be to use the proposed tests in this paper as a guard against under-specification of the propensity score. JEL Classifications: C21, C52 Key words: Propensity score, Specification, Monte Carlo *Research Fellow, Melbourne Institute of Applied Economic and Social Research, The University of Melbourne, Level 7, 161 Barry Street, Carlton, Victoria 3010, Australia. E-mail: [email protected]. Thanks to Jeff Borland, Michael Lechner, Jim Powell and Chris Skeels for comments on an earlier version of this paper. All errors are my own. 1. Introduction Despite being an important first step in implementing propensity score methods, the effect of misspecification of the propensity score model has not been subject to much scrutiny by researchers. In general, if the propensity score model is misspecified, the estimator of the propensity score will be inconsistent for the true propensity score and the resulting propensity score matching estimator may be inconsistent for estimating the average treatment effect. -

Chapter 14 Describing Relationships: Scatterplots and Correlation
Chapter 14 Describing Relationships: Scatterplots and Correlation We look at scatterplots and linear correlation for paired (bivariate) quantitative data sets. Scatterplot is graph of paired sampled data and linear correlation is a measure of linearity of scatterplot. Formula for linear correlation coefficient is 1 x − x¯ y − y¯ r = i i n − 1 sx sy ! X Exercise 14.1 (Describing Relationships: Scatterplots and Correlation) 1. Scatterplot: Reading Ability Versus Brightness. brightness, x 123456 7 8910 ability to read, y 70 70 75 88 91 94 100 92 90 85 100 y , ility Ab 80 Reading 60 0 2 4 6 8 10 Brightness, x Figure 14.1 (Scatterplot, Reading Ability Versus Brightness) Notice scatter plot may be misleading because y-axis ranges 60 to 80, rather than 0 to 80. 81 82Chapter 14. Describing Relationships: Scatterplots and Correlation (ATTENDANCE 8) (a) There are (circle one) 10 / 20 / 30 data points. One particular data point is (circle one) (70, 75) / (75, 2) / (2, 70). Data point (9,90) means (circle one) i. for brightness 9, reading ability is 90. ii. for reading ability 9, brightness is 90. (b) Reading ability positively / not / negatively associated to brightness. As brightness increases, reading ability (circle one) increases / decreases. (c) Association linear / nonlinear (curved) because straight line cannot be drawn on graph where all points of scatter fall on or near line. (d) “Reading ability” is response / explanatory variable on y–axis and “brightness” is response / explanatory variable on x–axis because read- ing ability depends on brightness, not the reverse. Sometimes the response variable and explanatory variable are not distinguished from one another. -

Regression Modelling and Other Methods to Control
REGRESSION MODELLING AND OTHER Occup Environ Med: first published as 10.1136/oem.2002.001115 on 16 June 2005. Downloaded from METHODS TO CONTROL 500 CONFOUNDING RMcNamee Occup Environ Med 2005;62:500–506. doi: 10.1136/oem.2002.001115 onfounding is a major concern in causal studies because it results in biased estimation of exposure effects. In the extreme, this can mean that a causal effect is suggested where none Cexists, or that a true effect is hidden. Typically, confounding occurs when there are differences between the exposed and unexposed groups in respect of independent risk factors for the disease of interest, for example, age or smoking habit; these independent factors are called confounders. Confounding can be reduced by matching in the study design but this can be difficult and/or wasteful of resources. Another possible approach—assuming data on the confounder(s) have been gathered—is to apply a statistical ‘‘correction’’ method during analysis. Such methods produce ‘‘adjusted’’ or ‘‘corrected’’ estimates of the effect of exposure; in theory, these estimates are no longer biased by the erstwhile confounders. Given the importance of confounding in epidemiology, statistical methods said to remove it deserve scrutiny. Many such methods involve strong assumptions about data relationships and their validity may depend on whether these assumptions are justified. Historically, the most common statistical approach for dealing with confounding in epidemiology was based on stratification; the standardised mortality ratio is a well known statistic using this method to remove confounding by age. Increasingly, this approach is being replaced by methods based on regression models.