DOCSLIB.ORG

1. Credit Derivatives. Credit Default Swap. Total Return Swap. Credit Forward

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1. Credit Derivatives. Credit Default Swap. Total Return Swap. Credit Forward FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] 1. Credit Derivatives. Credit Default Swap. Total Return Swap. Credit Forward. Credit Options. Credit forward Credit forward contracts provide symmetrical payoffs. The payoff at maturity of the forward contract may is determined by the following formula: [spread at maturity – contracted spread] x notional capital x risk factor Binary credit options There are two types of binary options with predetermined payouts, based on credit rating. payout predetermined payout option premium Credit Quality default no default Figure 1. Binary option with predetermined payout payout Credit Rating B2 B1 Ba3 Ba2 Ba1 investment grade Figure 2. Binary option based on a credit rating 1 FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] Credit Swaps Cash Payment if Credit risky Investment Credit Default Dealer Z assets protection (credit buyer protection (bank Y) seller) Total return Swap Premium Figure 3. Credit Default Swap with a Cash Payment Upon Default Credit risky Investment Credit LIBOR + spread Dealer Z assets protection (credit buyer protection (bank Y) seller) Total return Total return Figure 4. Credit Default Swap with a Periodic Payment Investor 1 Payment for a credit event associated Investor 2 Bond A with bond A Bond B Payment for a credit event associated with bond A 2 FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] Figure 5. Reciprocal Credit Default Swap Total Return Swap Credit risky Investment Credit LIBOR + spread Investor Y assets protection (credit risk buyer buyer) (dealer Z) Total return Total return Figure 6. Total Return Credit Swap 3 FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] Problem 1. Credit Forward Bank Y buys a credit spread forward. contracted credit spread 200 notional amount 1 000 000 risk factor 6,62 Required: Draw the payoff diagram for a long position in credit spread forward. Solution [spreadit spread - contracted credit spread] x notional amount x risk factor 100 -66 247 150 -33 123 200 0 215 9 937 230 19 874 245 29 811 260 39 748 275 49 685 290 59 622 Payoff Credit Spread Forward 60 000 40 000 20 000 0 100 120 140 160 180 200 220 240 260 280 300 -20 000 -40 000 -60 000 Credit Spread 4 FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] Problem 2. Credit Spread Call Option A dealer writes a credit spread call option. Origination date: 16-12-2005 Maturity date: 16-3-2006 Premium: 1,25% 125 basis points Notional principal: 1000000 zł Strike credit spread 2,00% Risk factor 6,62 Underlying asset: bonds issued by a company XYZ. Maturity: 16 grudzień 2015 Coupon: 8,00% (semiannual payments) The interest rates on the origination date and expiration date are following: 16-12 16-03 Risk-free rate 5,00% 4,90% Credit spread 2,00% 2,15% Required (a) Calculate the payoff of a short call option on bonds on the origination and the expiration dates. (b) What is the net payoff for a long position in credit spread call at maturity ? (c) Show the payoff's sensitivity on spread for a long position in credit spread call option. Solution (a) Price Date Yield Credit YTM Price Total Payoff Duration T spread of a bond value spot 16-12-2005 5,00% 2,00% 7,00% 107,11 1071062,02 6,93 strike 16-12-2005 5,00% 2,00% 7,00% 107,11 1071062,02 0,00 6,93 spot 16-3-2006 4,90% 2,15% 7,05% 106,60 1066005,69 6,69 strike 16-3-2006 4,90% 2,00% 6,90% 107,70 1076969,82 -10964,13 6,71 Premium 12500 Net payoff 1535,87 (b) [spread - contracted] x notional amount x risk factor - premium 0,0015 x 1000000 x 6,62 = 9937,04 -12500,00 -2562,96 (c) Spread Price Payoff Credit Spread Call Option 100 115,39 -12500,00 150 111,46 -12500,00 195000 200 107,70 -12500,00 165000 250 104,10 20623,48 135000 300 100,65 53746,95 105000 75000 350 97,35 86870,43 Payoff 45000 400 94,19 119993,91 15000 -15000 450 91,17 153117,38 100 150 200 250 300 350 400 450 500 500 88,26 186240,86 Credit Spread 5 FINANCIAL RISK MANAGEMENT AND DERIVATIVES [235221] 6.
Load more

Recommended publications
  • V. Black-Scholes Model: Derivation and Solution
    V. Black-Scholes model: Derivation and solution Beáta Stehlíková Financial derivatives, winter term 2014/2015 Faculty of Mathematics, Physics and Informatics Comenius University, Bratislava V. Black-Scholes model: Derivation and solution – p.1/36 Content Black-Scholes model: • Suppose that stock price follows a geometric ◦ S Brownian motion dS = µSdt + σSdw + other assumptions (in a moment) We derive a partial differential equation for the price of ◦ a derivative Two ways of derivations: • due to Black and Scholes ◦ due to Merton ◦ Explicit solution for European call and put options • V. Black-Scholes model: Derivation and solution – p.2/36 Assumptions Further assumptions (besides GBP): • constant riskless interest rate ◦ r no transaction costs ◦ it is possible to buy/sell any (also fractional) number of ◦ stocks; similarly with the cash no restrictions on short selling ◦ option is of European type ◦ Firstly, let us consider the case of a non-dividend paying • stock V. Black-Scholes model: Derivation and solution – p.3/36 Derivation I. - due to Black and Scholes Notation: • S = stock price, t =time V = V (S, t)= option price Portfolio: 1 option, stocks • δ P = value of the portfolio: P = V + δS Change in the portfolio value: • dP = dV + δdS From the assumptions: From the It¯o • dS = µSdt + σSdw, ∂V ∂V 1 2 2 ∂2V ∂V lemma: dV = ∂t + µS ∂S + 2 σ S ∂S2 dt + σS ∂S dw Therefore: • ∂V ∂V 1 ∂2V dP = + µS + σ2S2 + δµS dt ∂t ∂S 2 ∂S2 ∂V + σS + δσS dw ∂S V. Black-Scholes model: Derivation and solution – p.4/36 Derivation I.
    [Show full text]
  • Computation of Binomial Option Pricing Model with Parallel
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by KHALSA PUBLICATIONS I S S N 2 2 7 8 - 5 6 1 2 Volume 11 Number 5 International Journal of Management and Information T e c h n o l o g y Computation Of Binomial Option Pricing Model With Parallel Processing On A Linux Cluster Harya Widiputra Faculty of Information Technology, Perbanas Institute Jakarta, Indonesia [email protected] ABSTRACT Binary Option Pricing Model (BOPM) is one approach that can be utilized to calculate the value of either call or put option. BOPM generally works by building a binomial tree diagram, also known as lattice diagram to explore all possible option values that occur based on the intrinsic price of the underlying asset in a range of specific time period. Due to its basic characteristics BOPM is renowned for its longer lead times in calculating option values while also acknowledged as a technique that can provide an assessment of the most fair option value. Therefore, this study aims to shorten the BOPM completion time of calculating the value of an option by building a computer cluster and presently implement the BOPM algorithm into a form that can be run in parallel processing. As an outcome, a Linux-based computer cluster has been built and conversion of BOPM algorithm so that it can be executed in parallel has been performed and also implemented using Python in this research. Conclusively, results of conducted experiments confirm that the implementation of BOPM algorithm in a form that can be executed in parallel and its application on a computer cluster was able to limit the growth of the completion time whilst at the same time maintain quality of calculated option values.
    [Show full text]
  • Opposition, CFTC V. Banc De Binary
    Case 2:13-cv-00992-MMD-VCF Document 37 Filed 08/08/13 Page 1 of 30 Kathleen Banar, Chief Trial Attorney (IL Bar No. 6200597) David Slovick, Senior Trial Attorney (IL Bar No. 6257290) Margaret Aisenbrey, Trial Attorney (Mo Bar No. 59560) U.S. Commodity Futures Trading Commission 1155 21 St. NW Washington, DC 20581 [email protected], [email protected], [email protected] (202) 418-5335 (202) 418-5987 (facsimile) Blaine T. Welsh (NV Bar No. 4790) Assistant United States Attorney United States Attorney’s Office 333 Las Vegas Boulevard, Suite 5000 Las Vegas, Nevada 89101 [email protected] (702) 388-6336 (702) 388-6787 (facsimile) UNITED STATES DISTRICT COURT DISTRICT OF NEVADA ) U.S. COMMODITY FUTURES TRADING ) COMMISSION, ) ) Case No. 2:13-cv-00992-MMD-VCF Plaintiff, ) ) PLAINTIFF’S OPPOSITION TO v. ) DEFENDANT’S MOTION TO ) DISMISS COUNTS ONE, THREE ) AND FOUR OF THE COMPLAINT BANC DE BINARY LTD. (A/K/A E.T. ) BINARY OPTIONS LTD.), ) ) Defendant. ) ) 1 Case 2:13-cv-00992-MMD-VCF Document 37 Filed 08/08/13 Page 2 of 30 The United States Commodity Futures Trading Commission (“CFTC” or “Commission”) opposes Banc de Binary’s Motion to Dismiss Counts I, III and IV of the Complaint (“Defendant’s Motion”),1 and states as follows: I. SUMMARY Since at least May 2012 Banc de Binary Ltd. (A/K/A E.T. Binary Options) (“Banc de Binary” or “Defendant”) has been violating the CFTC’s long-standing ban on trading options contracts with persons located in the United States off of a contract market designated by the CFTC for that purpose (i.e., “off-exchange”).
    [Show full text]
  • Federal Register/Vol. 84, No. 215/Wednesday, November 6
    Federal Register / Vol. 84, No. 215 / Wednesday, November 6, 2019 / Notices 59849 respect to this action, see the each participant will speak, and the SECURITIES AND EXCHANGE application for license amendment time allotted for each presentation. COMMISSION dated October 23, 2019. A written summary of the hearing will [Release No. 34–87434; File No. SR– Attorney for licensee: General be compiled, and such summary will be NYSEArca–2019–12] Counsel, Tennessee Valley Authority, made available, upon written request to 400 West Summit Hill Drive, 6A West OPIC’s Corporate Secretary, at the cost Self-Regulatory Organizations; NYSE Tower, Knoxville, TN 37902. of reproduction. Arca, Inc.; Notice of Filing of NRC Branch Chief: Undine Shoop. Amendment No. 2 and Order Granting Written summaries of the projects to Accelerated Approval of a Proposed Dated at Rockville, Maryland, this 31st day be presented at the December 11, 2019, of October 2019. Rule Change, as Modified by Board meeting will be posted on OPIC’s Amendment No. 2, To List and Trade For the Nuclear Regulatory Commission. website. Kimberly J. Green, Shares of the iShares Commodity Senior Project Manager, Plant Licensing CONTACT PERSON FOR INFORMATION: Curve Carry Strategy ETF Under NYSE Branch II–2, Division of Operating Reactor Information on the hearing may be Arca Rule 8.600–E obtained from Catherine F. I. Andrade at Licensing, Office of Nuclear Reactor I. Introduction Regulation. (202) 336–8768, via facsimile at (202) [FR Doc. 2019–24198 Filed 11–5–19; 8:45 am] 408–0297, or via email at On March 1, 2019, NYSE Arca, Inc.
    [Show full text]
  • What Are Binary Options?
    PA R T I Introduction to Binary Options his section will provide you with an overview and discussion of the T main benefi ts of binary option trading. What You Will Learn: • What are binary options? • How do binary options differ from traditional options? • Which underlying instruments are binary options available to trade on? • Where can youhttp://www.pbookshop.com trade binary options? • What are the benefi ts of trading binary options? • What makes binary options unique compared to other instruments and options? COPYRIGHTED MATERIAL When you complete this section you should have a basic understand- ing of what binary options are and be familiar with their main advantages. 1 c01.indd 1 11/8/2012 4:12:44 PM http://www.pbookshop.com c01.indd 2 11/8/2012 4:12:44 PM CH A P T E R 1 What Are Binary Options? inary options are also known as digital options or all‐or‐nothing options. They are derivative instruments that can be considered a B yes‐or‐no proposition—either the event happens or it does not. Binary options are considered binary because there are only two po- tential outcomes at expiration: 0 or 100; 0 and 100 refer to the settlement value of a binary option and could be viewed in dollars. At expiration, if you are incorrect, you do not make anything ($0), and if you are correct, you make up to $100. The next section will go into further detail on the set- tlement value of binary options. ON WHAT ASSEThttp://www.pbookshop.com CLASSES ARE BINARY OPTIONS AVAILABLE? Binary options are available on four different asset classes.
    [Show full text]
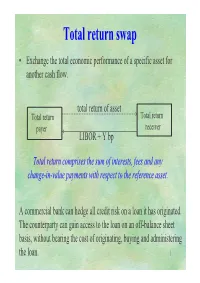
  • Total Return Swap • Exchange the Total Economic Performance of a Specific Asset for Another Cash Flow
    Total return swap • Exchange the total economic performance of a specific asset for another cash flow. total return of asset Total return Total return payer receiver LIBOR + Y bp Total return comprises the sum of interests, fees and any change-in-value payments with respect to the reference asset. A commercial bank can hedge all credit risk on a loan it has originated. The counterparty can gain access to the loan on an off-balance sheet basis, without bearing the cost of originating, buying and administering the loan. 1 The payments received by the total return receiver are: 1. The coupon c of the bond (if there were one since the last payment date Ti − 1) + 2. The price appreciation ( C ( T i ) − C ( T i − 1 ) ) of the underlying bond C since the last payment (if there were only). 3. The recovery value of the bond (if there were default). The payments made by the total return receiver are: 1. A regular fee of LIBOR + sTRS + 2. The price depreciation ( C ( T i − 1 ) − C ( T i ) ) of bond C since the last payment (if there were only). 3. The par value of the bond C if there were a default in the meantime). The coupon payments are netted and swap’s termination date is earlier than bond’s maturity. 2 Some essential features 1. The receiver is synthetically long the reference asset without having to fund the investment up front. He has almost the same payoff stream as if he had invested in risky bond directly and funded this investment at LIBOR + sTRS.
    [Show full text]
  • Credit Derivatives
    3 Credit Derivatives CHAPTER 7 Credit derivatives Collaterized debt obligation Credit default swap Credit spread options Credit linked notes Risks in credit derivatives Credit Derivatives •A credit derivative is a financial instrument whose value is determined by the default risk of the principal asset. •Financial assets like forward, options and swaps form a part of Credit derivatives •Borrowers can default and the lender will need protection against such default and in reality, a credit derivative is a way to insure such losses Credit Derivatives •Credit default swaps (CDS), total return swap, credit default swap options, collateralized debt obligations (CDO) and credit spread forwards are some examples of credit derivatives •The credit quality of the borrower as well as the third party plays an important role in determining the credit derivative’s value Credit Derivatives •Credit derivatives are fundamentally divided into two categories: funded credit derivatives and unfunded credit derivatives. •There is a contract between both the parties stating the responsibility of each party with regard to its payment without resorting to any asset class Credit Derivatives •The level of risk differs in different cases depending on the third party and a fee is decided based on the appropriate risk level by both the parties. •Financial assets like forward, options and swaps form a part of Credit derivatives •The price for these instruments changes with change in the credit risk of agents such as investors and government Credit derivatives Collaterized debt obligation Credit default swap Credit spread options Credit linked notes Risks in credit derivatives Collaterized Debt obligation •CDOs or Collateralized Debt Obligation are financial instruments that banks and other financial institutions use to repackage individual loans into a product sold to investors on the secondary market.
    [Show full text]
  • How to Trade Binary Options Successfully
    How to Trade Binary Options Successfully A Complete Guide to Binary Options Trading By Meir Liraz ___________________________________________________________________ Revealed At Last! The Best Kept Secret Among Successful Binary Options and Forex Traders The Easiest Way to Make Money Trading Online ___________________________________________________________________ Published by BizMove Binary Options Trading Center Copyright © Meir Liraz. All Rights Reserved. Our Preferred Binary Options Broker We currently trade at this broker. After testing several Binary Options and Forex platforms we find this one to be the best. What made the difference is a unique feature that allow us to watch and copy the strategies and trades of the best performing traders on the platform. You can actually see each move the "Guru" traders make. This method works nicely for us. Since we started trading at this broker we noticed an increase of our successful trades and profits when compared to our former brokers. Having said that, please note that all trading involves risk. Only risk capital you're prepared to lose. Past performance does not guarantee future results. This post is for educational purposes and should not be considered as investment advice. Table of Contents 1. The Single Most Critical Factor to Binary Options Trading Success 2. What are Binary Options 3. The Flow of Decisions in a Binary Options Trade 4. Advantages and Disadvantages of Binary Options Trading 5. Binary Trading Risk Management 6. What You Need to Succeed in Binary Options 7. How Much Money You Need to Start Trading 8. Technical Analysis As a Tool for Binary Trading Success 9. Developing a Binary Options Strategy and Entry Signals 10.
    [Show full text]
  • On Black-Scholes Equation, Black- Scholes Formula and Binary Option Price
    On Black-Scholes Equation, Black- Scholes Formula and Binary Option Price Chi Gao 12/15/2013 Abstract: I. Black-Scholes Equation is derived using two methods: (1) risk-neutral measure; (2) - hedge. II. The Black-Scholes Formula (the price of European call option is calculated) is calculated using two methods: (1) risk-neutral pricing formula (expected discounted payoff) (2) directly solving the Black-Scholes equation with boundary conditions III. The two methods in II are proved to be essentially equivalent. The Black-Scholes formula for European call option is tested to be the solution of Black-Scholes equation. IV. The value of digital options and share digitals are calculated. The European call and put options are be replicated by digital options and share digitals, thus the prices of call and put options can be derived from the values of digitals. The put-call parity relation is given. 1. The derivation(s) of Black-Scholes Equation Black Scholes model has several assumptions: 1. Constant risk-free interest rate: r 2. Constant drift and volatility of stock price: 3. The stock doesn’t pay dividend 4. No arbitrage 5. No transaction fee or cost 6. Possible to borrow and lend any amount (even fractional) of cash at the riskless rate 7. Possible to buy and sell any amount (even fractional) of stock A typical way to derive the Black-Scholes equation is to claim that under the measure that no arbitrage is allowed (risk-neutral measure), the drift of stock price equal to the risk-free interest rate . That is (usually under risk-neutral measure, we write Brownian motion as , here we remove Q subscript for convenience ) (1) Then apply Ito’s lemma to the discounted price of derivatives , we get [ ] [( ) ] (2) Still, under risk-neutral measure we can argue that is martingale.
    [Show full text]
  • Introduction Section 4000.1
    Introduction Section 4000.1 This section contains product profiles of finan- Each product profile contains a general cial instruments that examiners may encounter description of the product, its basic character- during the course of their review of capital- istics and features, a depiction of the market- markets and trading activities. Knowledge of place, market transparency, and the product’s specific financial instruments is essential for uses. The profiles also discuss pricing conven- examiners’ successful review of these activities. tions, hedging issues, risks, accounting, risk- These product profiles are intended as a general based capital treatments, and legal limitations. reference for examiners; they are not intended to Finally, each profile contains references for be independently comprehensive but are struc- more information. tured to give a basic overview of the instruments. Trading and Capital-Markets Activities Manual February 1998 Page 1 Federal Funds Section 4005.1 GENERAL DESCRIPTION commonly used to transfer funds between depository institutions: Federal funds (fed funds) are reserves held in a bank’s Federal Reserve Bank account. If a bank • The selling institution authorizes its district holds more fed funds than is required to cover Federal Reserve Bank to debit its reserve its Regulation D reserve requirement, those account and credit the reserve account of the excess reserves may be lent to another financial buying institution. Fedwire, the Federal institution with an account at a Federal Reserve Reserve’s electronic funds and securities trans- Bank. To the borrowing institution, these funds fer network, is used to complete the transfer are fed funds purchased. To the lending institu- with immediate settlement.
    [Show full text]
  • Commodity Index Traders and the Boom/Bust Cycle in Commodities Prices
    Page 2 Commodity Index Traders and the Boom/Bust Cycle in Commodities Prices David Frenk and Wallace Turbeville* ©Better Markets 2011 ABSTRACT Since 2005, the public has lived with high and volatile prices for basic energy and agricultural commodities. The public focus on this unprecedented commodity price volatility has been intense, because a large proportion of the cost of living borne by individuals and families in the U.S. (and around the globe) is represented by commodities- based costs, notably food, fuel, and clothing. Interestingly, as commodity prices have shown more price volatility, there has been an accompanying significant increase in the volume of commodities futures and swaps transactions, as well as commodities markets open interest. Moreover, Commodity Index Traders (“CITs”), a relatively new type of participant, now collectively make up the single largest group of non-commercial participants in commodities futures markets. These CITs, which represent giant institutional pools of capital, have at times been the single largest class of participant, outweighing bona fide hedgers (producers and consumers of commodities) and traditional “speculators,” who take short-term bi-directional bets and provide liquidity. Given both the size and the specific and largely homogeneous investment strategy of the CITs, many market observers have concluded that this group is most likely responsible for greatly disrupting price formation in commodities futures markets. Further, it has been posited that this distortion has directly led to
    [Show full text]
  • Pricing Credit Default Swaps with Parisian and Parasian Default Mechanics
    University of Wollongong Research Online Faculty of Engineering and Information Faculty of Engineering and Information Sciences - Papers: Part B Sciences 2019 Pricing credit default swaps with Parisian and Parasian default mechanics Wenting Chen Jiangnan University, [email protected] Xinjiang He University of Wollongong, [email protected] Sha Lin Zhejiang Gongshang University, [email protected] Follow this and additional works at: https://ro.uow.edu.au/eispapers1 Part of the Engineering Commons, and the Science and Technology Studies Commons Recommended Citation Chen, Wenting; He, Xinjiang; and Lin, Sha, "Pricing credit default swaps with Parisian and Parasian default mechanics" (2019). Faculty of Engineering and Information Sciences - Papers: Part B. 3189. https://ro.uow.edu.au/eispapers1/3189 Research Online is the open access institutional repository for the University of Wollongong. For further information contact the UOW Library: [email protected] Pricing credit default swaps with Parisian and Parasian default mechanics Abstract This paper proposes Parisian and Parasian default mechanics for modeling the credit risks of the CDS (credit default swap) contracts. Unlike most of the structural models used in the literature, our new model assumes that the default will occur only if the price of the reference asset stays below a certain level for a pre-described period of time. To work out the corresponding CDS price, a general pricing formula containing the unknown no-default probability is derived first. It is then shown that the determination of such a probability is equivalent to the valuation of a Parisian or Parasian down-and-out binary options, depending on how the time is recorded.
    [Show full text]