Comparing Two Flywheel-Piston Linkages
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Installation Guide R2.8 CM2220 R101B
Installation Guide R2.8 CM2220 R101B Copyright© 2018 Bulletin 5504137 Cummins Inc. Printed 10-JANUARY-2018 All rights reserved To buy Cummins Parts and Service Manuals, Training Guides, or Tools go to our website at https://store.cummins.com Foreword Thank you for depending on Cummins® products. If you have any questions about this product, please contact your Cummins® Authorized Repair Location. You can also visit cumminsengines.com or quickserve.cummins.com for more information, or go to locator.cummins.com for Cummins® distributor and dealer locations and contact information. Read and follow all safety instructions. See the General Safety Instructions in Section i - Introduction. To buy Cummins Parts and Service Manuals, Training Guides, or Tools go to our website at https://store.cummins.com Table of Contents Section Introduction ........................................................................................................................................................ i Engine and System Identification .................................................................................................................... E Pre-Install Preparation ...................................................................................................................................... 1 Installation .......................................................................................................................................................... 2 Pre-Start Preparation ........................................................................................................................................ -

Theory of Machines
THEORY OF MACHINES For MECHANICAL ENGINEERING THEORY OF MACHINES & VIBRATIONS SYLLABUS Theory of Machines: Displacement, velocity and acceleration analysis of plane mechanisms; dynamic analysis of linkages; cams; gears and gear trains; flywheels and governors; balancing of reciprocating and rotating masses; gyroscope. Vibrations: Free and forced vibration of single degree of freedom systems, effect of damping; vibration isolation; resonance; critical speeds of shafts. ANALYSIS OF GATE PAPERS Exam Year 1 Mark Ques. 2 Mark Ques. Total 2003 6 - 15 2004 8 - 18 2005 6 - 14 2006 9 - 21 2007 1 6 13 2008 1 3 7 2009 2 4 10 2010 5 3 11 2011 1 3 7 2012 2 1 4 2013 3 2 7 2014 Set-1 2 3 8 2014 Set-2 2 3 8 2014 Set-3 2 4 10 2014 Set-4 2 3 8 2015 Set-1 1 2 5 2015 Set-2 2 2 6 2015 Set-3 3 3 9 2016 Set-1 2 3 8 2016 Set-2 1 2 5 2016 Set-3 3 3 9 2017 Set-1 1 3 7 2017 Set-2 2 4 10 2018 Set-1 2 3 8 2018 Set-2 2 1 4 © Copyright Reserved by Gateflix.in No part of this material should be copied or reproduced without permission CONTENTS Topics Page No 1. MECHANICS 1.1 Introduction 01 1.2 Kinematic chain 05 1.3 3-D Space Mechanism 07 1.4 Bull Engine / Pendulum Pump 12 1.5 Basic Instantaneous centers in the mechanism 15 1.6 Theorem of Angular Velocities 16 1.7 Mechanical Advantage of the mechanism 22 2. -

Theoretical and Experimental Investigation of a Kinematically Driven Flywheel for Reducing Rotational Vibrations
11th International Conference on Vibration Problems Z. Dimitrovova´ et.al. (eds.) Lisbon, Portugal, 9–12 September 2013 THEORETICAL AND EXPERIMENTAL INVESTIGATION OF A KINEMATICALLY DRIVEN FLYWHEEL FOR REDUCING ROTATIONAL VIBRATIONS M. Pfabe*1, C. Woernle1 1University of Rostock fmathias.pfabe, [email protected] Keywords: rotational vibration, torque compensation, driven flywheel, gear wheel mechanism, combustion engine Abstract. Modern turbocharged internal combustion engines induce high fluctuating torques at the crankshaft. They result in rotational crankshaft vibrations that are transferred both to the gearbox and the auxiliary engine systems. To reduce the rotational crankshaft vibrations, a passive mechanical device for compensating fluctuating engine torques has been developed. It comprises a flywheel that is coupled to the crankshaft by means of a non-uniformly transmit- ting mechanism. The kinematical transfer behavior of the mechanism is synthesized in such a manner that the inertia torque of the flywheel compensates at least one harmonic of the fluc- tuating engine torque. The degree of non-uniformity of the mechanism has to be adapted to the actual load and rotational speed of the engine. As a solution, a double-crank mechanism with cycloidal-crank input and adjustable crank length is proposed and analyzed. Parameter synthesis is achieved by means of a simplified mechanical model that calculates the required transfer function for a given engine torque. To analyze the overall dynamic behavior, the device is modeled in a multibody domain. Simulation results are validated using an electrically driven test rig. Comparisons between simulation and experimental results demonstrate the potential of the device. M. Pfabe, C. Woernle 1 Introduction The strong demand for more efficient automobiles forces the development of so-called down- sized combustion engines with high specific power. -
Piston Crown Markings All in the Piston Crown
PISTON CROWN MARKINGS ALL IN THE PISTON CROWN The different piston crown markings and what they mean: Looking at a piston, the markings on the piston crown attract attention. In addition to dimensional and clearance specifications, most pistons show information about their fitting orientation. The pistons are marked with fitting orientations according to specifications from our production customers – the engine manufacturers. Many customers – this means also many different requests and specifications for piston markings. This multitude of markings may appear to the onlooker somewhat like Egyptian hieroglyphs. For this reason, we are giving you here an overview of the most important markings and their meaning: SYMBOL FITTING ORIENTATION IN ENGINE EXAMPLE Steering side (opposite power output/clutch) MB, VW, Opel, BMW Flywheel (power output/clutch) Peugeot, Opel Notch Steering side (opposite power output/clutch) Perkins, Opel (cast-in) Steering side (opposite power output/clutch) „AV“ stands for the AV Citroen, Renault French word „avant“ = in front Flywheel (power output/clutch) „AR“ stands for the French word „ar- Citroen, Renault AR rière“ = at the back Flywheel (power output/clutch) „V“ stands for the French word „vo- V Renault, Peugeot lant“ = flywheel Flywheel (power output/clutch) Renault, Peugeot, Citroen FRONT Steering side (opposite power output/clutch) GM, Perkins vorn Steering side (opposite power output/clutch) Hatz, Liebherr Abluft Exhaust-air side for some air cooled engine Deutz, MWM Special case for two-stroke engines: direction exhaust manifold Zündapp, Husqvarna Special case for some V engines: direction engine centre MB Why is it important to observe the fitting orientation for pistons? Pistons with asymmetric crown shape or pistons that are designed with different sizes of valve pockets in the piston head can only be fitted to the engine in a particular orientation. -

ZF Microcommand User Manual
INSTALLATION, OPERATION AND TROUBLESHOOTING MM9110 - MICROCOMMANDER USER MANUAL MARINE PROPULSION SYSTEMS COPYRIGHT Released by After Sales dept. Data subject to change without notice. We decline all responsibility for the use of non-original components or accessories wich have not been tested and submitted for approval. =)UHVHUYHVDOOULJKWVUHJDUGLQJWKHVKRZQWHFKQLFDOLQIRUPDWLRQLQFOXGLQJWKHULJKWWRÀOHLQGXVWULDOSURSHUW\ULJKWDSSOLFD - tions and the industrial property rights resulting from these in Germany and abroad. © ZF Friedrichshafen AG, 2014. 2 EN 3340.758.008a - 2014-10 TABLE OF CONTENT Table of Contents SW15623.0P MicroCommander User Manual..................................................... 1 Table of Contents .................................................................................3 Preface ...............................................................................................15 Revision List .......................................................................................19 1 Introduction........................................................................................21 1.1 Basic Theory of Operation............................................................................................................... 21 1.2 System Features.............................................................................................................................. 21 2 Operation ...........................................................................................23 2.1 DC Power On.................................................................................................................................. -

The Modeling for Flywheel Mass with Parameters of Crank & Linkage in Engine
ISSN 2664-4150 (Print) & ISSN 2664-794X (Online) South Asian Research Journal of Engineering and Technology Abbreviated Key Title: South Asian Res J Eng Tech | Volume-3 | Issue-3 | May-Jun -2021 | DOI: 10.36346/sarjet.2021.v03i03.008 Review Article The Modeling for Flywheel Mass with Parameters of Crank & Linkage in Engine Run Xu* Yantai University, WenJing College, Mechanical Electricity Department,Yantai 264005, China *Corresponding Author Run Xu Article History Received: 19.05.2021 Accepted: 23.06.2021 Published: 28.06.2021 Abstract: The mass of flywheel will incline as the punch speed inclines; it will decline as radius inclines. It would incline when the punch mould mass inclines. So it is chosen that big radius and small mould mass for saving cost of material and machine. The biggest mass of flywheel is about 10Kg at 0.1m of radius and 7Kg of piston at the time of 0.06s and crank length R=75mm and linkage length L=255mm. So it is important for us to choose the piston mass. If it is 5Kg the biggest one will 10Kg at the time of 0.06s and crank length R=80mm and linkage length L=245mm then choosing crank length is second factor. Keywords: Modelling; flywheel; piston mass; radius; engine; parameter; cost control. 1. INTRODUCTION relieved impact and speed, it has many places to apply in modern industrial field. So it needs to be investigated in detail with a certain parameters for its wide usefulness in many machines. So in this study the flywheel mass with the rotation speed and its radius is modeled to find a certain intrinsic relations for process of motor housing punch. -

Analysis and Control of a Flywheel Hybrid Vehicular Powertrain Shuiwen Shen and Frans E
IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, VOL. 12, NO. 5, SEPTEMBER 2004 645 Analysis and Control of a Flywheel Hybrid Vehicular Powertrain Shuiwen Shen and Frans E. Veldpaus Abstract—Vehicular powertrains with an internal combustion Zero inertia ratio. engine, an electronic throttle valve, and a continuously variable External disturbance torque. transmission (CVT) offer much freedom in controlling the engine Vehicle road load torque. speed and torque. This can be used to improve fuel economy by operating the engine in fuel-optimal operating points. The main Desired engine torque. drawbacks of this approach are the low driveability and, possibly, Induced engine torque. an inverse response of the vehicle acceleration after a kick-down Roll resistance. of the drive pedal. This paper analyzes a concept for a novel pow- Torque in drive shafts. ertrain with an additional flywheel. The flywheel plays a part only Driver pedal angle. in transient situations by (partly) compensating the engine inertia, making it possible to optimize fuel economy in stationary situations Powertrain efficiency. without loosing driveability in transients. Two control strategies Engine speed. are discussed. The first one focuses on the engine and combines Desired engine speed. feedback linearization with proportional control of the CVT ratio. Flywheel speed. The CVT controller has to be combined with an engine torque con- Wheel speed. troller. Three possibilities for this controller are discussed. In the second strategy, focusing on control of the vehicle speed, a bifur- Desired wheel speed. cation occurs whenever a downshift of the CVT to the minimum Throttle opening. ratio is demanded. Some methods to overcome this problem are introduced. -

Flywheels and Super-Fly Wheels - B
ENERGY STORAGE SYSTEMS – Vol. I – Flywheels and Super-Fly Wheels - B. Kaftanoğlu FLYWHEELS AND SUPER-FLYWHEELS B. Kaftanoğlu Middle East Technical University, Ankara, TURKEY Keywords: Flywheel, super-flywheel, energy storage, composites. Contents 1. Introduction 2. Applications 3. Flywheel design 4. Historical perspective of flywheel design 5. Stress Analysis and Specific Energy Calculations of Flywheels 5.1. Stress Analysis of Isotropic Multi-hyperbolic Flywheels 5.2. Interference Fit for Multi-hyperbolic Flywheels 5.3. Specific Energy for Multi-hyperbolic Flywheels 5.4. Stress Analysis of Composite Multi-rim Flyweels 5.5. Elastic Constants and Allowable Stresses for Multi-rim Flywheels 5.6. Specific Energy for Multi-rim Flywheels 6. Sample solutions for Design Optimization of Flywheels 7. Discussions of Design Optimization 7. 1. Multi-hyperbolic Flywheels 7.2. Multi-rim Flywheels 8. Concluding remarks Acknowledgements Appendix Glossary Bibliography Biographical Sketch Summary This chapter introduces the use of the flywheels for mechanical energy storage. The need for flywheels is discussed and the amounts of energy stored by different techniquesUNESCO are compared with that stored – by flywheels.EOLSS Some historical information is given and previous work is briefly surveyed. Then design of clasical flywheels is introduced. The design of super flywheels made out of composite materials are discussed and theorySAMPLE for multi-hyperbolic and CHAPTERSmulti-rim flywheels are presented.. 1. Introduction Strorage of energy is necessary in many applications because of the following needs: Energy may be available when it is not needed, and conversely energy may be needed when it is not available. ©Encyclopedia of Life Support Systems (EOLSS) ENERGY STORAGE SYSTEMS – Vol. -
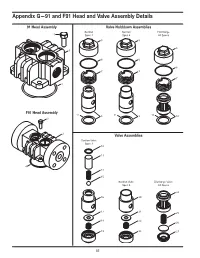
Appendix G—91 and F91 Head and Valve Assembly Details
Appendix G—91 and F91 Head and Valve Assembly Details 91 Head Assembly Valve Holddown Assemblies Suction Suction Discharge 3 Spec 3 Spec 4 All Specs 5 5 5 1 6 6 6 7 7 7 4 F91 Head Assembly 11 8 11 9 11 10 3 2 Valve Assemblies Suction Valve Spec 3 12 13 4 14 15 Suction Valve Discharge Valve Spec 4 All Specs 24 16 20 17 21 25 18 22 26 19 23 27 52 Appendix G—91 and F91 Head and Valve Assembly Details Head and Valve Bill of Materials Ref Part No. Description No. 2374 Head model 91 1. 2374-Xa Head assy. for model 91 (spec 3) 2374-X1 Head assy. for model 91 (spec 4) 2. 4302 Head model F91 (ANSI flange) 3. 7001-037 NC100A Bolt, 3/8-16 x 1" Gr.5 hex head 4. 2-235_c O-ring 5. 2714-1 Valve cap 6. 2-031_c O-ring 7. 2715 Holddown screw 3483-1X Suction valve assy. (spec 3) 8. 3483-1X1b Same as above but with copper gaskets 3483-1X2b Same as above but with iron-lead gaskets 3483-X Suction valve assy. (spec 4) 9. 3483-X1b Same as above but with copper gaskets 3483-X2b Same as above but with iron-lead gaskets 3485-X Discharge valve assy. (all specs) 10. 3485-X1b Same as above but with copper gaskets 3485-X2b Same as above but with iron-lead gaskets 2717 Valve gasket (aluminum) 11. 2717-1b Valve gasket (copper) 2717-2b Valve gasket (iron-lead) 12. -

Flywheel Energy Storage for Automotive Applications
Energies 2015, 8, 10636-10663; doi:10.3390/en81010636 OPEN ACCESS energies ISSN 1996-1073 www.mdpi.com/journal/energies Review Flywheel Energy Storage for Automotive Applications Magnus Hedlund *, Johan Lundin, Juan de Santiago, Johan Abrahamsson and Hans Bernhoff Division for Electricity, Uppsala University, Lägerhyddsvägen 1, Uppsala 752 37, Sweden; E-Mails: [email protected] (J.L.); [email protected] (J.S.); [email protected] (J.A.); [email protected] (H.B.) * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +46-18-471-5804. Academic Editor: Joeri Van Mierlo Received: 25 July 2015 / Accepted: 12 September 2015 / Published: 25 September 2015 Abstract: A review of flywheel energy storage technology was made, with a special focus on the progress in automotive applications. We found that there are at least 26 university research groups and 27 companies contributing to flywheel technology development. Flywheels are seen to excel in high-power applications, placing them closer in functionality to supercapacitors than to batteries. Examples of flywheels optimized for vehicular applications were found with a specific power of 5.5 kW/kg and a specific energy of 3.5 Wh/kg. Another flywheel system had 3.15 kW/kg and 6.4 Wh/kg, which can be compared to a state-of-the-art supercapacitor vehicular system with 1.7 kW/kg and 2.3 Wh/kg, respectively. Flywheel energy storage is reaching maturity, with 500 flywheel power buffer systems being deployed for London buses (resulting in fuel savings of over 20%), 400 flywheels in operation for grid frequency regulation and many hundreds more installed for uninterruptible power supply (UPS) applications. -

Service Manual
CH18-CH25, CH620-CH730, CH740, CH750 Service Manual IMPORTANT: Read all safety precautions and instructions carefully before operating equipment. Refer to operating instruction of equipment that this engine powers. Ensure engine is stopped and level before performing any maintenance or service. 2 Safety 3 Maintenance 5 Specifi cations 14 Tools and Aids 17 Troubleshooting 21 Air Cleaner/Intake 22 Fuel System 28 Governor System 30 Lubrication System 32 Electrical System 48 Starter System 57 Clutch 59 Disassembly/Inspection and Service 72 Reassembly 24 690 06 Rev. C KohlerEngines.com 1 Safety SAFETY PRECAUTIONS WARNING: A hazard that could result in death, serious injury, or substantial property damage. CAUTION: A hazard that could result in minor personal injury or property damage. NOTE: is used to notify people of important installation, operation, or maintenance information. WARNING WARNING CAUTION Explosive Fuel can cause Accidental Starts can Electrical Shock can fi res and severe burns. cause severe injury or cause injury. Do not fi ll fuel tank while death. Do not touch wires while engine is hot or running. Disconnect and ground engine is running. Gasoline is extremely fl ammable spark plug lead(s) before and its vapors can explode if servicing. CAUTION ignited. Store gasoline only in approved containers, in well Before working on engine or Damaging Crankshaft ventilated, unoccupied buildings, equipment, disable engine as and Flywheel can cause away from sparks or fl ames. follows: 1) Disconnect spark plug personal injury. Spilled fuel could ignite if it comes lead(s). 2) Disconnect negative (–) in contact with hot parts or sparks battery cable from battery. -

ATK-Cdale 2004-2015 450 Engine Parts Manual
Throttle Body 1 * 14 13 16 12 15 2 * 3 5 7 9 22 18 20 4 21 17 23 19 8 6 10 11 23 1 5001148 COUPLING, THROTTLE BODY 22 2 5001149 CLAMP, BAND 21 2 5001561 WASHER,M5 20 1 5000513 BTTNHD TORX SCREW, M5X35 19 1 5000512 BTTNHD TORX SCREW, M5X25 18 1 5001973 BYPASS GASKET 17 1 5001972 BYPASS HOUSING 16 2 5001974 SCREW, PHILLIPS, 10X5/8 15 1 5001971 BYPASS ACTUATOR 14 2 5001489 BHCS, M4X12 mm 13 1 5000409 THROTTLE POSITION SENSOR 12 1 5001401 THROTTLE BODY SLEEVE 11 1 5001581 NUT, HEX M8 X 1.0 10 1 5000959 LOCK WASHER, M8 91 5002307 THROTTLE CABLE PULLEY 81 5000688 THROTTLE SPRING 72 5002305 THROTTLE SPRING SLEEVE 61 6000502 IDLE ADJUSTMENT SCREW 51 5001346 IDLE ADJUSTMENT THUMBWHEEL 41 5000827 SPRING, IDLE ADJUST THUMBWHEEL 33 5001473 BHCS, M4X8 mm *1 6001121 XTHROTTLE CABLE STOP 21 5002308X THROTTLE CABLE STOP *1 6000767 XTHROTTLE BODY ASSEMBLY 11 5002340X THROTTLE BODY ASSEMBLY ITEM QTY DEA LER PA RT M/C A TV DESCRIPTION NOTES NO REQD NUMBER MODEL THROTTLE BODY PARTS LIST 2 Fuel Injectors * 7 9 6 * 8 9 1 1 5 11 2 3 3 10 4 4 11 2 5001545 O-RING, FUEL INJECTOR, TOP 10 2 5001546 O-RING, FUEL INJECTOR, BOTTOM 91 5002321 HOSE SHEATH, BULK 5’ LENGTH *1 6000317 XHOSE, FUEL, 350 mm TO FUEL REGULATOR 81 5002204-03X HOSE, FUEL, REG TO INJECTOR TO FUEL REGULATOR 71 5002324 HOSE, FUEL, 6.4 mm ID, 60 mm *1 6000318 XHOSE, FUEL, 130 mm TO FUEL PUMP 61 5002203-02X HOSE, FUEL, PUMP TO INJECTOR TO FUEL PUMP 52 5000478-06 FUEL INJECTOR BASE 42 5001458 NUT, HEX FLANGE, M3 32 5000171 FUEL INJECTOR CLIP 21351-5000166 FUEL INJECTOR SET INCLUDES FLOW RATE VALUE 14