DOCSLIB.ORG

Noise and Distortion in Microwave System

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Noise and Distortion in Microwave System Noise and Distortion in Microwave System Prof. Tzong-Lin Wu EMC Laboratory Department of Electrical Engineering National Taiwan University 2016/3/16 MW & RF Design / Prof. T. -L. Wu 1 Introduction Noise is a random process from many sources: thermal, atmosphere, inter-stellar radiation and man-made radiation. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 2 3.1 Review of Random Processes Probability and Random Variables 2016/3/16 MW & RF Design / Prof. T. -L. Wu 3 3.1 Review of Random Processes Cumulative Distribution Function The cumulative distribution function (CDF), Fx(x), of the random variable X is defined as the probability that X is less than or equal to a particular value, x. Properties: Monotonic (non decreasing) function 2016/3/16 MW & RF Design / Prof. T. -L. Wu 4 3.1 Review of Random Processes Probability Density Function The probability density function (PDF)of a random variable X is defined as the derivative of the CDF: 2016/3/16 MW & RF Design / Prof. T. -L. Wu 5 3.1 Review of Random Processes Probability Density Function PDF and CDF with 2 random variables Joint CDF associated with random variables X and Y is defined as the joint PDF is calculated as The probability of x and y both occurring in given ranges is found from 2016/3/16 MW & RF Design / Prof. T. -L. Wu 6 3.1 Review of Random Processes Probability Density Function The individual probability density functions for X and Y can be recovered from the joint PDF by integration over one of the variables: Statistically independent 2016/3/16 MW & RF Design / Prof. T. -L. Wu 7 3.1 Review of Random Processes Some Important Probability Density Functions Uniform distribution Gaussian distribution where m is the mean of the distribution, and is the variance. Rayleigh distribution 2016/3/16 MW & RF Design / Prof. T. -L. Wu 8 3.1 Review of Random Processes Expected Values The expected value is also sometimes called the mean, or average value. For discrete random variables Continuous random variables: Taking the expected value of a random variable is a linear operation Expected value of a function of a random variable Discrete case Continuous random variable 2016/3/16 MW & RF Design / Prof. T. -L. Wu 9 Higher order statistical average nth moment of the random variable The variance, Expected value of joint PDF Independent random variables: 2016/3/16 MW & RF Design / Prof. T. -L. Wu 10 3.1 Review of Random Processes Autocorrelation Autocorrelation: how fast a signal changes with time Defined for a complex deterministic signal, x(t) For stationary random processes, such as noise Power spectral density (PSD) 2016/3/16 MW & RF Design / Prof. T. -L. Wu 11 3.1 Review of Random Processes Autocorrelation Power delivered to 1 load is For a noise voltage, the power spectral density represents the noise power density in the spectral (frequency) domain, assuming a 1ohm load resistor. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 12 2016/3/16 MW & RF Design / Prof. T. -L. Wu 13 2016/3/16 MW & RF Design / Prof. T. -L. Wu 14 2016/3/16 MW & RF Design / Prof. T. -L. Wu 15 3.2 Thermal Noise • Random motion of charge carrier. • Also called Nyquist, or Johnson noise • Most important source of noise in microwave band. • Other noise: shot noise, flicker, plasma, quantum Shot noise, due to the random motion of charge carriers in electron tubes and solid-state devices; flicker noise, also occurring in solid-sate devices and vacuum tubes; plasma noise, caused by random motions of charged particles in an ionized gas or sparking electrical contacts; Quantum noise, resulting from the quantized nature of charge carriers and photons. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 16 3.2 Thermal Noise Noise Voltage and Power Rayleigh Jeans approximation: The electrons in the resistor are in random motion, with a kinetic energy that is proportional to the temperature, T. These random motions produce small random voltage fluctuations across the terminals of the resistor. The mean value of this voltage is zero, but its nonzero rms value in a narrow frequency bandwidth B is given by 2016/3/16 MW & RF Design / Prof. T. -L. Wu 17 3.2 Thermal Noise Noise Voltage and Power The noisy resistor can be modeled using a Thevenin equivalent circuit as an ideal (noiseless) resistor with a voltage generator to represent the noise voltage. The available noise power is defined as the maximum power that can be delivered from the noise source to a load resistor. Note that the noise power decreases as the system bandwidth decrease. This implies that systems with smaller bandwidths collect less noise power. Noise power decreases as temperature decreases, which implies that internally generated noise effects can be reduced by cooling a system to low temperatures. Since thermal noise power is independent of frequency, it is referred to as white noise 2016/3/16 MW & RF Design / Prof. T. -L. Wu 18 3.2 Thermal Noise Noise Voltage and Power Noise spectrum is flat from DC~1000GHz Two-sided power spectral density Autocorrelation of a white noise PDF of white noise: Gaussian with zero mean 2016/3/16 MW & RF Design / Prof. T. -L. Wu 19 Since the variance of the sum of two independent random variables is the sum of the individual variances (see Problem 3.5) The variance is equivalent to power delivered to a 1 Q load, the noise powers generated by two independent noise sources add in a common load. This is in contrast to the case of deterministic sources, where voltages add. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 20 Ex 3.2 2016/3/16 MW & RF Design / Prof. T. -L. Wu 21 3.3 NOISE IN LINEAR SYSTEMS In a wireless radio receiver, both desired signals and undesired noise pass through various stages, such as RF amplifiers, filters, and mixers. These functions generally alter the statistical properties of the noise, and so it is useful to study these effects by considering the general case of transmission of noise through a linear system. Autocorrelation and Power Spectral Density in Linear Systems 2016/3/16 MW & RF Design / Prof. T. -L. Wu 22 3.3 Noise in Linear Systems Autocorrelation and Power Spectral Density in Linear Systems This result shows that the autocorrelation of the output is given by the double convolution of the autocorrelation of the input with the impulse response: 2016/3/16 MW & RF Design / Prof. T. -L. Wu 23 Autocorrelation and Power Spectral Density in Linear Systems the equivalent result in terms of power spectral density 2016/3/16 MW & RF Design / Prof. T. -L. Wu 24 3.3 Noise in Linear Systems Gaussian White Noise through an Ideal Low-pass Filter Filter notation The output noise power is proportional to the filter bandwidth. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 25 3.3 Noise in Linear Systems Gaussian White Noise through an Integrator 2016/3/16 MW & RF Design / Prof. T. -L. Wu 26 3.3 Noise in Linear Systems Mixing of Noise LO signal with random phase: This result shows that mixing reduces the average noise power by half. In this case, the 2 factor of one-half is due to the ensemble averaging of the cos w0t term over the range of random phase. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 27 3.3 Noise in Linear Systems Mixing of Noise LO signal with deterministic phase: The variance of the output signal is now a function of time, and represents the instantaneous power of the output signal. To find the time-average output power, we must take the time average of the variance We see that the same average output power is obtained whether the averaging is over the ensemble phase variation, or over time. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 28 2016/3/16 MW & RF Design / Prof. T. -L. Wu 29 3.3 Noise in Linear Systems Narrowband Representation of Noise Gaussian white noise passing through a bandpass filter with a center frequency w0 and bandwidth Δw. x(t) and y(t) are random processes, but are slowly varying due to the narrow bandwidth of the filter. How to prove the valid of this form? 2016/3/16 MW & RF Design / Prof. T. -L. Wu 30 3.3 Noise in Linear Systems Narrowband Representation of Noise After low-pass filtering with a low-pass cutoff frequency of , only the x(t) and y(t) terms will remain in the above results. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 31 We now find the statistics of x(t) and y(t), and show that these Gaussian random processes have zero mean, the same variance as n(t), and are uncorrelated. 2016/3/16 MW & RF Design / Prof. T. -L. Wu 32 3.3 Noise in Linear Systems Narrowband Representation of Noise Comparing (3.48) to (3.47) shows that Meaning? 2016/3/16 MW & RF Design / Prof. T. -L. Wu 33 3.3 Noise in Linear Systems Narrowband Representation of Noise Ans: 2016/3/16 MW & RF Design / Prof. T. -L. Wu 34 3.4 Basic Threshold Detection 2016/3/16 MW & RF Design / Prof. T. -L. Wu 35 Probability of error When a binary "1" is transmitted, a detection error will occur if the received signal and noise is less than the threshold level at the sampling time. For a threshold of vo/2, the probability of this event is Gaussian probability density function set Lower limit Define: complementary error function: 2016/3/16 MW & RF Design / Prof.
Load more

Recommended publications
  • Problems in Residential Design for Ventilation and Noise
    Proceedings of the Institute of Acoustics PROBLEMS IN RESIDENTIAL DESIGN FOR VENTILATION AND NOISE J Harvie-Clark Apex Acoustics Ltd, Gateshead, UK (email: [email protected]) M J Siddall LEAP : Low Energy Architectural Practice, Durham, UK (email: [email protected]) & Northumbria University, Newcastle upon Tyne, UK ([email protected]) 1. ABSTRACT This paper addresses three broad problems in residential design for achieving sufficient ventilation provision with reasonable internal ambient noise levels. The first problem is insufficient qualification of the ventilation conditions that should be achieved while meeting the internal ambient noise level limits. Requirements from different Planning Authorities vary widely; qualification of the ventilation condition is proposed. The second problem concerns the feasibility of natural ventilation with background ventilators; the practical result falls between Building Control and Planning Authority such that appropriate ventilation and internal noise limits may not both be achieved. Greater coordination between planning guidance and Building Regulations is suggested. The third problem concerns noise from mechanical systems that is currently entirely unregulated, yet again can preclude residents from enjoying reasonable indoor air quality and noise levels simultaneously. Surveys from over 1000 dwellings are reviewed, and suitable noise limits for mechanical services are identified. It is suggested that commissioning measurements by third party accredited bodies are required in all cases as the only reliable means to ensure that that the intended conditions are achieved in practice. 2. INTRODUCTION The adverse effects of noise on residents are well known; the general limits for internal ambient noise levels are described in the World Health Organisations Guidelines for Community Noise (GCN)1, Night Noise Guidelines (NNG)3 and BS 82332.
    [Show full text]
  • Noise Tutorial Part IV ~ Noise Factor
    Noise Tutorial Part IV ~ Noise Factor Whitham D. Reeve Anchorage, Alaska USA See last page for document information Noise Tutorial IV ~ Noise Factor Abstract: With the exception of some solar radio bursts, the extraterrestrial emissions received on Earth’s surface are very weak. Noise places a limit on the minimum detection capabilities of a radio telescope and may mask or corrupt these weak emissions. An understanding of noise and its measurement will help observers minimize its effects. This paper is a tutorial and includes six parts. Table of Contents Page Part I ~ Noise Concepts 1-1 Introduction 1-2 Basic noise sources 1-3 Noise amplitude 1-4 References Part II ~ Additional Noise Concepts 2-1 Noise spectrum 2-2 Noise bandwidth 2-3 Noise temperature 2-4 Noise power 2-5 Combinations of noisy resistors 2-6 References Part III ~ Attenuator and Amplifier Noise 3-1 Attenuation effects on noise temperature 3-2 Amplifier noise 3-3 Cascaded amplifiers 3-4 References Part IV ~ Noise Factor 4-1 Noise factor and noise figure 4-1 4-2 Noise factor of cascaded devices 4-7 4-3 References 4-11 Part V ~ Noise Measurements Concepts 5-1 General considerations for noise factor measurements 5-2 Noise factor measurements with the Y-factor method 5-3 References Part VI ~ Noise Measurements with a Spectrum Analyzer 6-1 Noise factor measurements with a spectrum analyzer 6-2 References See last page for document information Noise Tutorial IV ~ Noise Factor Part IV ~ Noise Factor 4-1. Noise factor and noise figure Noise factor and noise figure indicates the noisiness of a radio frequency device by comparing it to a reference noise source.
    [Show full text]
  • Next Topic: NOISE
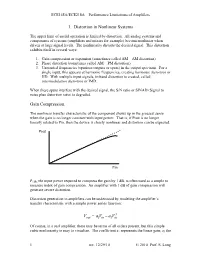
    ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize.
    [Show full text]
  • Monitoring the Acoustic Performance of Low- Noise Pavements
    Monitoring the acoustic performance of low- noise pavements Carlos Ribeiro Bruitparif, France. Fanny Mietlicki Bruitparif, France. Matthieu Sineau Bruitparif, France. Jérôme Lefebvre City of Paris, France. Kevin Ibtaten City of Paris, France. Summary In 2012, the City of Paris began an experiment on a 200 m section of the Paris ring road to test the use of low-noise pavement surfaces and their acoustic and mechanical durability over time, in a context of heavy road traffic. At the end of the HARMONICA project supported by the European LIFE project, Bruitparif maintained a permanent noise measurement station in order to monitor the acoustic efficiency of the pavement over several years. Similar follow-ups have recently been implemented by Bruitparif in the vicinity of dwellings near major road infrastructures crossing Ile- de-France territory, such as the A4 and A6 motorways. The operation of the permanent measurement stations will allow the acoustic performance of the new pavements to be monitored over time. Bruitparif is a partner in the European LIFE "COOL AND LOW NOISE ASPHALT" project led by the City of Paris. The aim of this project is to test three innovative asphalt pavement formulas to fight against noise pollution and global warming at three sites in Paris that are heavily exposed to road noise. Asphalt mixes combine sound, thermal and mechanical properties, in particular durability. 1. Introduction than 1.2 million vehicles with up to 270,000 vehicles per day in some places): Reducing noise generated by road traffic in urban x the publication by Bruitparif of the results of areas involves a combination of several actions.
    [Show full text]
  • Noise Figure Measurements Application Note
    Application Note Noise Figure Measurements VectorStar Making successful, confident NF measurements on Amplifiers The Anritsu VectorStar’s Noise Figure – Option 041 enables the capability to measure noise figure (NF), which is the degradation of the signal-to-noise ratio caused by components in a signal chain. The NF measurement is based on a cold source technique for improved accuracy. Various levels of match and fixture correction are available for additional enhancement. VectorStar is the only VNA platform offering a Noise Figure option enabling NF measurements from 70 kHz to 125 GHz. It is also the only VNA platform available with an optimized noise receiver for measurements from 30 to 125 GHz. 1. NF Overview 1.1. NF Definition 1.2. Importance of Accurate NF Measurements 2. NF Measurement Methods 2.1. Y-Factor / Hot-Cold Noise Figure Measurement Method 2.2. Cold-Source Noise Figure Measurement Method 3. NF Measurement Process 3.1. Test Preparation / Setup 3.2. Instrument Setup 3.3. Measurement Procedure 4. Measurement Example 5. Uncertainties 5.1. Uncertainty Calculator 6. Calculation Example 7. Measurement Tips and Considerations 8. References / Additional Resources 1. NF Overview 1.1 NF Definition Noise figure is a figure-of-merit that describes the degradation of signal-to-noise ratio (SNR) due to added output noise power (No) of a device or system when presented with thermal noise at the input at standard noise temperature (T0, typically 290 K). For amplifiers, the concept can be readily seen. Ideally, when a noiseless input signal is applied to an amplifier, the output signal is simply the input multiplied by the amplifier gain.
    [Show full text]
  • Quantum Noise and Quantum Measurement
    Quantum noise and quantum measurement Aashish A. Clerk Department of Physics, McGill University, Montreal, Quebec, Canada H3A 2T8 1 Contents 1 Introduction 1 2 Quantum noise spectral densities: some essential features 2 2.1 Classical noise basics 2 2.2 Quantum noise spectral densities 3 2.3 Brief example: current noise of a quantum point contact 9 2.4 Heisenberg inequality on detector quantum noise 10 3 Quantum limit on QND qubit detection 16 3.1 Measurement rate and dephasing rate 16 3.2 Efficiency ratio 18 3.3 Example: QPC detector 20 3.4 Significance of the quantum limit on QND qubit detection 23 3.5 QND quantum limit beyond linear response 23 4 Quantum limit on linear amplification: the op-amp mode 24 4.1 Weak continuous position detection 24 4.2 A possible correlation-based loophole? 26 4.3 Power gain 27 4.4 Simplifications for a detector with ideal quantum noise and large power gain 30 4.5 Derivation of the quantum limit 30 4.6 Noise temperature 33 4.7 Quantum limit on an \op-amp" style voltage amplifier 33 5 Quantum limit on a linear-amplifier: scattering mode 38 5.1 Caves-Haus formulation of the scattering-mode quantum limit 38 5.2 Bosonic Scattering Description of a Two-Port Amplifier 41 References 50 1 Introduction The fact that quantum mechanics can place restrictions on our ability to make measurements is something we all encounter in our first quantum mechanics class. One is typically presented with the example of the Heisenberg microscope (Heisenberg, 1930), where the position of a particle is measured by scattering light off it.
    [Show full text]
  • Evolution of the Soundscape Following the Traffic Closure on the Right Bank of the Seine in Paris
    Evolution of the soundscape following the traffic closure on the right bank of the Seine in Paris Fanny Mietlicki Bruitparif, France. Matthieu Sineau Bruitparif, France.. Summary Since September 2016, by decision of the City of Paris, the right bank of the Seine river is closed to traffic along 3.3 km. Bruitparif has put in place a system for assessment of the modifications on the sound environment brought by this closure. This system was based on the implementation of noise measurements at 90 sites in and around Paris as well as modeling. At the end of a year of follow-up, it was possible to establish the following observations: 1. Partial traffic shifts to the lanes located above the banks have generated an increase in traffic noise for residents. This is more pronounced at night (up to 4 dB (A) in some areas) than during the day (less than 2 dB (A) increase). However, during daytime there is an increase of noise peaks (horns, sirens of emergency vehicles ...) related to rising congestion. 2. Other axes in Paris have also undergone a slight increase in noise likely related to the traffic reports, but in a more limited manner (of the order of 1 dB (A)). 3. Outside Paris, especially on the ring road and major roads, no significant change has been noted. 4. At the end of a year of observation, there does not seem to have been an adaptation of the behavior of drivers. 5. On the other hand, traffic noise has clearly decreased on the bank which is now pedestrianized, as well as on the façades of the first buildings located opposite the right banks of the Seine river.
    [Show full text]
  • CHAPTER 20. NOISE ANALYSIS and LOW NOISE DESIGN
    Circuits, Devices, Networks, and Microelectronics CHAPTER 20. NOISE ANALYSIS and LOW NOISE DESIGN 20.1 THE ORIGINS OF NOISE Electrical noise is a background “grass” of unwanted signals, usually due to thermal origins. It has a nearly constant amplitude density across the frequency spectrum that tends to mask and obscure the waveforms and information which we wish for our circuits to process. Noise is an inescapable fact of circuits and signals. It is generated in most part by thermal fluctuations in the motion and flow of charge. It is an important factor in the design and analysis of communication circuits, and therefore most treatments of noise are developed in the context of communications electronics. But electrical noise, and its companion problem, distortion, are an important and necessary consideration of any circuit, in which a signal, whether of linear or logic form, is to be processed. A figure of merit that defines a circuit in terms of its signal transfer properties is the dynamic range (DR) given by The smallest usable signal level is defined by the noise limit. The largest usable signal is defined by the distortion limit, which is usually a consequence of the compliance (±VS) limits of the circuit. In matters of electrical noise, components and devices are defined by thermal kinetics. Thermal statistical fluctuations will produce a random set of signals within an electrical component. Thermal effects manifest themselves as fluctuations in electrical currents. The basic unit of thermal energy (fluctuation) is given by w = kT (defined by the fugacity for electrons), where k = Boltzmann’s constant and T = absolute temperature.
    [Show full text]
  • Noise Figure
    Master Degree (LM) in Electronic Engineering MICROWAVES NOISE AND NON-LINEAR DISTORTION Prof. Luca Perregrini Università di Pavia, Facoltà di Ingegneria [email protected] http://microwave.unipv.it/perregrini/ Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 1 SUMMARY Chapter 10 Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 2 SUMMARY • Dynamic range and sources of noise • Noise power, equivalent noise temperature, measurement of noise temperature • Noise figure of a component and of a cascaded system • Noise figure of a passive two-port network, a mismatched lossy line, a mismatched amplifier • Nonlinear distortion • Gain compression • Harmonic and intermodulation distortion • Third-order intercept point • Intercept point of a cascaded system • Linear and spurious free dynamic range Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 3 MOTIVATION Noise is critical to the performance of most RF and microwave communications, radar, and remote sensing systems. Noise determines the threshold for the minimum signal that can be reliably detected by a receiver. Noise power in a receiver will be introduced from the external environment through the receiving antenna, as well as generated internally by the receiver circuitry. The sources of noise in RF and microwave systems, and the characterization of components in terms of noise temperature and noise figure, including the effect of impedance mismatch, will be studied. Compression, harmonic distortion, intermodulation distortion, and dynamic range will also be discussed. These can have important limiting effects when large signal levels are present in mixers, amplifiers, and other components that use nonlinear devices such as diodes and transistors.
    [Show full text]
  • Local Noise Action Plans
    Practitioner Handbook for Local Noise Action Plans Recommendations from the SILENCE project SILENCE is an Integrated Project co-funded by the European Commission under the Sixth Framework Programme for R&D, Priority 6 Sustainable Development, Global Change and Ecosystems Guidance for readers Step 1: Getting started – responsibilities and competences • These pages give an overview on the steps of action planning and Objective To defi ne a leader with suffi cient capacities and competences to the noise abatement measures and are especially interesting for successfully setting up a local noise action plan. To involve all relevant stakeholders and make them contribute to the implementation of the plan clear competences with the leading department are needed. The END ... DECISION MAKERS and TRANSPORT PLANNERS. Content Requirements of the END and any other national or The current responsibilities for noise abatement within the local regional legislation regarding authorities will be considered and it will be assessed whether these noise abatement should be institutional settings are well fi tted for the complex task of noise considered from the very action planning. It might be advisable to attribute the leadership to beginning! another department or even to create a new organisation. The organisational settings for steering and carrying out the work to be done will be decided. The fi nancial situation will be clarifi ed. A work plan will be set up. If support from external experts is needed, it will be determined in this stage. To keep in mind For many departments, noise action planning will be an additional task. It is necessary to convince them of the benefi ts and the synergies with other policy fi elds and to include persons in the steering and working group that are willing and able to promote the issue within their departments.
    [Show full text]
  • Understanding Noise Figure
    Understanding Noise Figure Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul One of the most frequently discussed forms of noise is known as Thermal Noise. Thermal noise is a random fluctuation in voltage caused by the random motion of charge carriers in any conducting medium at a temperature above absolute zero (K=273 + °Celsius). This cannot exist at absolute zero because charge carriers cannot move at absolute zero. As the name implies, the amount of the thermal noise is to imagine a simple resistor at a temperature above absolute zero. If we use a very sensitive oscilloscope probe across the resistor, we can see a very small AC noise being generated by the resistor. • The RMS voltage is proportional to the temperature of the resistor and how resistive it is. Larger resistances and higher temperatures generate more noise. The formula to find the RMS thermal noise voltage Vn of a resistor in a specified bandwidth is given by Nyquist equation: Vn = 4kTRB where: k = Boltzmann constant (1.38 x 10-23 Joules/Kelvin) T = Temperature in Kelvin (K= 273+°Celsius) (Kelvin is not referred to or typeset as a degree) R = Resistance in Ohms B = Bandwidth in Hz in which the noise is observed (RMS voltage measured across the resistor is also function of the bandwidth in which the measurement is made). As an example, a 100 kΩ resistor in 1MHz bandwidth will add noise to the circuit as follows: -23 3 6 ½ Vn = (4*1.38*10 *300*100*10 *1*10 ) = 40.7 μV RMS • Low impedances are desirable in low noise circuits.
    [Show full text]
  • Link Budgets 1
    Link Budgets 1 Intuitive Guide to Principles of Communications www.complextoreal.com Link Budgets You are planning a vacation. You estimate that you will need $1000 dollars to pay for the hotels, restaurants, food etc.. You start your vacation and watch the money get spent at each stop. When you get home, you pat yourself on the back for a job well done because you still have $50 left in your wallet. We do something similar with communication links, called creating a link budget. The traveler is the signal and instead of dollars it starts out with “power”. It spends its power (or attenuates, in engineering terminology) as it travels, be it wired or wireless. Just as you can use a credit card along the way for extra money infusion, the signal can get extra power infusion along the way from intermediate amplifiers such as microwave repeaters for telephone links or from satellite transponders for satellite links. The designer hopes that the signal will complete its trip with just enough power to be decoded at the receiver with the desired signal quality. In our example, we started our trip with $1000 because we wanted a budget vacation. But what if our goal was a first-class vacation with stays at five-star hotels, best shows and travel by QE2? A $1000 budget would not be enough and possibly we will need instead $5000. The quality of the trip desired determines how much money we need to take along. With signals, the quality is measured by the Bit Error Rate (BER).
    [Show full text]