DOCSLIB.ORG

CHAPTER 20. NOISE ANALYSIS and LOW NOISE DESIGN

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CHAPTER 20. NOISE ANALYSIS and LOW NOISE DESIGN Circuits, Devices, Networks, and Microelectronics CHAPTER 20. NOISE ANALYSIS and LOW NOISE DESIGN 20.1 THE ORIGINS OF NOISE Electrical noise is a background “grass” of unwanted signals, usually due to thermal origins. It has a nearly constant amplitude density across the frequency spectrum that tends to mask and obscure the waveforms and information which we wish for our circuits to process. Noise is an inescapable fact of circuits and signals. It is generated in most part by thermal fluctuations in the motion and flow of charge. It is an important factor in the design and analysis of communication circuits, and therefore most treatments of noise are developed in the context of communications electronics. But electrical noise, and its companion problem, distortion, are an important and necessary consideration of any circuit, in which a signal, whether of linear or logic form, is to be processed. A figure of merit that defines a circuit in terms of its signal transfer properties is the dynamic range (DR) given by The smallest usable signal level is defined by the noise limit. The largest usable signal is defined by the distortion limit, which is usually a consequence of the compliance (±VS) limits of the circuit. In matters of electrical noise, components and devices are defined by thermal kinetics. Thermal statistical fluctuations will produce a random set of signals within an electrical component. Thermal effects manifest themselves as fluctuations in electrical currents. The basic unit of thermal energy (fluctuation) is given by w = kT (defined by the fugacity for electrons), where k = Boltzmann’s constant and T = absolute temperature. Translate that into the fluctuations in power and p w B kT B (20.1-2a) where B = bandwidth of the frequencies passed by the circuit. Since power usually relates to signal through resistance then the (rms) noise thermal power is 2 2 p en R in G (20.1-2b) where R = resistance and G = conductance. These give noise signals in terms of en = noise voltage and in = noise current. The maximum signal that can be passed from the source, = the resistance itself, (according to maximum power transfer) is then 511 Circuits, Devices, Networks, and Microelectronics 2 en 4kTRB (20.1-3a) or 2 in 4kTGB (20.1-3a) Equation (20.1-3) is called Johnson-Nyquist’s theorem. Note that the measure is in terms of a mean square noise voltage (or current). Consider the following example: EXAMPLE 20.1-1: What is the amplitude en of the thermal noise associated with a resistance R = 1k at a noise bandwidth B = 1 MHz? kT SOLUTION: e 2 4kTRB 4 q R B n q = 4 × .025 × (1.602 × 10 -19) × 103 × 106 s-1 = (1.602 × 10-20) × 109 V2 = 16 × 10-12 V2 The calculation assumes that the circuit is at room temperature (~300K) for which kT/q = VT (= thermal voltage) .025V. The 4kT term has value 4kT = 1.6 × 10-20 (room temperature) and this value may be adopted as a shortcut default for most situations involving noise analysis. Taking the square root gives noise amplitude en = 4V Equations (20.1-3a) and (20.1-3b) may be represented by the network equivalents of figure 20.1-1 Figure 20.1-1: Equivalent circuits for thermal noise. This type of noise is also called Johnson noise, or white (full spectrum) noise since it is spread uniformly across all frequencies of the spectrum. It is also called thermal noise since it is a result of thermal statistics. 512 Circuits, Devices, Networks, and Microelectronics Even though each resistance contributes noise as its own little noise source and the network can be analyzed as if it were a collection of noise sources and resistances, this would be a challenging and totally useless exercise. The only place that it finds merit is in circuit simulation, where a part-by-part analysis might be appropriate. Use of Thevenin theorem to reduce the network to a single source and resistance works just fine. The only reason that the separated analysis might be of benefit is for sensitivity analysis of each resistance, and that is a task that is more appropriate for circuit simulation software. Assessment of a network with both resistances and reactive components implies the need for an expanded form of equation (20.1-3). This expanded form is the Nyquist formula and is given by e 2 2kT R( f )df 4kT R( f )df (20.1-4) n 0 where R( f ) is the real part of the impedance Z( f ), as seen across the output nodes. The Nyquist formula can also be written as e 2 4kTR G( f )df 4kTRB n 0 2 2 for which G( f ) is the (frequency dependent) power gain = vout /vin , assuming the resistance term R is separable. And it gives a clear definition of the noise bandwidth. Consider the following example: EXAMPLE 20.1-2: Consider the single-time constant RC network shown by figure 20.1-2. Using the 2 Nyquist formula find (a) noise signal en and (b) noise bandwidth B. Figure 20.1-2: Single-time constant RC network. 1 R SOLUTION: The impedance looking into the output is Z G sC 1 jRC R and its real component is ReZ( f ) R( f ) 1 2 R 2C 2 513 Circuits, Devices, Networks, and Microelectronics The Nyquist formula then gives R 4kT RCd 4kTR 1 1 e 2 4kT df 4kTR n 2 2 2 2C 2 2 2 2 RC 2 2RC 2 0 1 R C 0 1 R C and the noise bandwidth is B f3dB 2 Note that the noise bandwidth is greater than the (STC) 3dB bandwidth by the factor /2. Extending this outcome as an approximation to all circuit networks is not unreasonable and so noise bandwidth will then be expected to relate to the circuit (3dB) bandwidth as: 1 Noise bandwidth = B f (20.1-5) 2 3dB 4 3dB 20.2 SYSTEM NOISE ANALYSIS Noise is a form of background signal. In this respect it should be expected that the detector/transducer at the front end of the circuit is the major source of the noise, in terms of some sort of ‘dark current’ signal, with characteristics as might be represented by the source resistance RS. But it is also true that the components within the amplifier/interface circuit also contribute noise, and it is the assessment of the system noise factors that is necessary to identifying the noise characteristics of the system. The quantitative comparison between carrier signal and noise signal is defined by the signal-noise ratio (20.2-1) Both signal S and noise N are amplified by the gain factor G of the amplifier. But the noise NO at the output is greater than the amplified input noise = G × Ni, courtesy of the additional noise contributed by the components within the amplifier, i.e. N O GN i N Oa GN i GN a G(N i N a ) (20.2-2) 514 Circuits, Devices, Networks, and Microelectronics where NOa = additional noise at the output = GNa. It is as if an additional noise source Na exists at the input. The sum (Ni + Na) is then an equivalent noise input, and it gives a means to define the principal noise characteristic for the system ≡ the noise factor F, identified by the ratio Ni N a N a F 1 (20.2-3) Ni Ni Take note that F is always greater than unity. Equation (20.2-3) can be restated in terms of the power gain G = SO/Si, where SO and Si represent the signal levels at output and input, respectively of the system, i.e. NO NO Si Ni F (20.2-4) GNi SO Si Ni SO NO i.e. the noise factor also represents the degradation of the S/N due to the system. It is important to note that the signal-to-noise and noise factor are ratio relationships of signal power. The maximum signal power transferred and consequently the maximum available noise power per bandwidth occurs when Rin = RS, for which 2 en 4kTRS B N i kTB (20.2-5) 4RS 4RS and N kT B T F 1 a 1 e 1 e (20.2-6) kTB kTB T Equation (20.2-6) shows that the noise character of a system has a corollary parameter in the form of an equivalent noise temperature Te for which Te (F 1) T (20.2-7) EXAMPLE 20.2-1: Noise factor F = 2.5 corresponds to Te (2.5 1) 300 = 450K (The nominal circuit temperature T is assumed to be = 300K.) 515 Circuits, Devices, Networks, and Microelectronics Since the ultimate interest is the dynamic range of the system, a lower limit, or smallest usable signal, must be identified. This limit is defined as the noise floor Nf = Si(min) needed to achieve a given output S/N. A corollary to this definition is the minimum detectible signal, which is the input signal voltage 2 vi(min) associated with the noise floor. Assuming that Si vi RS , the minimum detectible signal is then vi (min) 4RS Si (min) (20.2-8) From the definition (20.2-4) of noise factor in terms of S/N ratios, and assuming the systems are matched, (for which Rin = RS) then SO SO N f Si (min) Ni F kTB F (20.2-9) NO NO EXAMPLE 20.2-2: What is the noise floor and minimum detectible signal for a system with bandwidth 20kHz, noise factor 8dB, input resistance Rin = 50 if the output signal/noise requirement is 10dB.
Load more

Recommended publications
  • Problems in Residential Design for Ventilation and Noise
    Proceedings of the Institute of Acoustics PROBLEMS IN RESIDENTIAL DESIGN FOR VENTILATION AND NOISE J Harvie-Clark Apex Acoustics Ltd, Gateshead, UK (email: [email protected]) M J Siddall LEAP : Low Energy Architectural Practice, Durham, UK (email: [email protected]) & Northumbria University, Newcastle upon Tyne, UK ([email protected]) 1. ABSTRACT This paper addresses three broad problems in residential design for achieving sufficient ventilation provision with reasonable internal ambient noise levels. The first problem is insufficient qualification of the ventilation conditions that should be achieved while meeting the internal ambient noise level limits. Requirements from different Planning Authorities vary widely; qualification of the ventilation condition is proposed. The second problem concerns the feasibility of natural ventilation with background ventilators; the practical result falls between Building Control and Planning Authority such that appropriate ventilation and internal noise limits may not both be achieved. Greater coordination between planning guidance and Building Regulations is suggested. The third problem concerns noise from mechanical systems that is currently entirely unregulated, yet again can preclude residents from enjoying reasonable indoor air quality and noise levels simultaneously. Surveys from over 1000 dwellings are reviewed, and suitable noise limits for mechanical services are identified. It is suggested that commissioning measurements by third party accredited bodies are required in all cases as the only reliable means to ensure that that the intended conditions are achieved in practice. 2. INTRODUCTION The adverse effects of noise on residents are well known; the general limits for internal ambient noise levels are described in the World Health Organisations Guidelines for Community Noise (GCN)1, Night Noise Guidelines (NNG)3 and BS 82332.
    [Show full text]
  • Noise Tutorial Part IV ~ Noise Factor
    Noise Tutorial Part IV ~ Noise Factor Whitham D. Reeve Anchorage, Alaska USA See last page for document information Noise Tutorial IV ~ Noise Factor Abstract: With the exception of some solar radio bursts, the extraterrestrial emissions received on Earth’s surface are very weak. Noise places a limit on the minimum detection capabilities of a radio telescope and may mask or corrupt these weak emissions. An understanding of noise and its measurement will help observers minimize its effects. This paper is a tutorial and includes six parts. Table of Contents Page Part I ~ Noise Concepts 1-1 Introduction 1-2 Basic noise sources 1-3 Noise amplitude 1-4 References Part II ~ Additional Noise Concepts 2-1 Noise spectrum 2-2 Noise bandwidth 2-3 Noise temperature 2-4 Noise power 2-5 Combinations of noisy resistors 2-6 References Part III ~ Attenuator and Amplifier Noise 3-1 Attenuation effects on noise temperature 3-2 Amplifier noise 3-3 Cascaded amplifiers 3-4 References Part IV ~ Noise Factor 4-1 Noise factor and noise figure 4-1 4-2 Noise factor of cascaded devices 4-7 4-3 References 4-11 Part V ~ Noise Measurements Concepts 5-1 General considerations for noise factor measurements 5-2 Noise factor measurements with the Y-factor method 5-3 References Part VI ~ Noise Measurements with a Spectrum Analyzer 6-1 Noise factor measurements with a spectrum analyzer 6-2 References See last page for document information Noise Tutorial IV ~ Noise Factor Part IV ~ Noise Factor 4-1. Noise factor and noise figure Noise factor and noise figure indicates the noisiness of a radio frequency device by comparing it to a reference noise source.
    [Show full text]
  • Measurement of In-Band Optical Noise Spectral Density 1
    Measurement of In-Band Optical Noise Spectral Density 1 Measurement of In-Band Optical Noise Spectral Density Sylvain Almonacil, Matteo Lonardi, Philippe Jennevé and Nicolas Dubreuil We present a method to measure the spectral density of in-band optical transmission impairments without coherent electrical reception and digital signal processing at the receiver. We determine the method’s accuracy by numerical simulations and show experimentally its feasibility, including the measure of in-band nonlinear distortions power densities. I. INTRODUCTION UBIQUITUS and accurate measurement of the noise power, and its spectral characteristics, as well as the determination and quantification of the different noise sources are required to design future dynamic, low-margin, and intelligent optical networks, especially in open cable design, where the optical line must be intrinsically characterized. In optical communications, performance is degraded by a plurality of impairments, such as the amplified spontaneous emission (ASE) due to Erbium doped-fiber amplifiers (EDFAs), the transmitter-receiver (TX-RX) imperfection noise, and the power-dependent Kerr-induced nonlinear impairments (NLI) [1]. Optical spectrum-based measurement techniques are routinely used to measure the out-of-band optical signal-to-noise ratio (OSNR) [2]. However, they fail in providing a correct assessment of the signal-to-noise ratio (SNR) and in-band noise statistical properties. Whereas the ASE noise is uniformly distributed in the whole EDFA spectral band, TX-RX noise and NLI mainly occur within the signal band [3]. Once the latter impairments dominate, optical spectrum-based OSNR monitoring fails to predict the system performance [4]. Lately, the scientific community has significantly worked on assessing the noise spectral characteristics and their impact on the SNR, trying to exploit the information in the digital domain by digital signal processing (DSP) or machine learning.
    [Show full text]
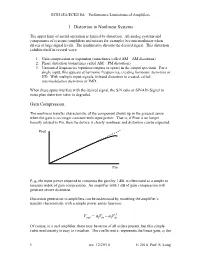
  • Next Topic: NOISE
    ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize.
    [Show full text]
  • Monitoring the Acoustic Performance of Low- Noise Pavements
    Monitoring the acoustic performance of low- noise pavements Carlos Ribeiro Bruitparif, France. Fanny Mietlicki Bruitparif, France. Matthieu Sineau Bruitparif, France. Jérôme Lefebvre City of Paris, France. Kevin Ibtaten City of Paris, France. Summary In 2012, the City of Paris began an experiment on a 200 m section of the Paris ring road to test the use of low-noise pavement surfaces and their acoustic and mechanical durability over time, in a context of heavy road traffic. At the end of the HARMONICA project supported by the European LIFE project, Bruitparif maintained a permanent noise measurement station in order to monitor the acoustic efficiency of the pavement over several years. Similar follow-ups have recently been implemented by Bruitparif in the vicinity of dwellings near major road infrastructures crossing Ile- de-France territory, such as the A4 and A6 motorways. The operation of the permanent measurement stations will allow the acoustic performance of the new pavements to be monitored over time. Bruitparif is a partner in the European LIFE "COOL AND LOW NOISE ASPHALT" project led by the City of Paris. The aim of this project is to test three innovative asphalt pavement formulas to fight against noise pollution and global warming at three sites in Paris that are heavily exposed to road noise. Asphalt mixes combine sound, thermal and mechanical properties, in particular durability. 1. Introduction than 1.2 million vehicles with up to 270,000 vehicles per day in some places): Reducing noise generated by road traffic in urban x the publication by Bruitparif of the results of areas involves a combination of several actions.
    [Show full text]
  • Receiver Sensitivity and Equivalent Noise Bandwidth Receiver Sensitivity and Equivalent Noise Bandwidth
    11/08/2016 Receiver Sensitivity and Equivalent Noise Bandwidth Receiver Sensitivity and Equivalent Noise Bandwidth Parent Category: 2014 HFE By Dennis Layne Introduction Receivers often contain narrow bandpass hardware filters as well as narrow lowpass filters implemented in digital signal processing (DSP). The equivalent noise bandwidth (ENBW) is a way to understand the noise floor that is present in these filters. To predict the sensitivity of a receiver design it is critical to understand noise including ENBW. This paper will cover each of the building block characteristics used to calculate receiver sensitivity and then put them together to make the calculation. Receiver Sensitivity Receiver sensitivity is a measure of the ability of a receiver to demodulate and get information from a weak signal. We quantify sensitivity as the lowest signal power level from which we can get useful information. In an Analog FM system the standard figure of merit for usable information is SINAD, a ratio of demodulated audio signal to noise. In digital systems receive signal quality is measured by calculating the ratio of bits received that are wrong to the total number of bits received. This is called Bit Error Rate (BER). Most Land Mobile radio systems use one of these figures of merit to quantify sensitivity. To measure sensitivity, we apply a desired signal and reduce the signal power until the quality threshold is met. SINAD SINAD is a term used for the Signal to Noise and Distortion ratio and is a type of audio signal to noise ratio. In an analog FM system, demodulated audio signal to noise ratio is an indication of RF signal quality.
    [Show full text]
  • Noise Figure Measurements Application Note
    Application Note Noise Figure Measurements VectorStar Making successful, confident NF measurements on Amplifiers The Anritsu VectorStar’s Noise Figure – Option 041 enables the capability to measure noise figure (NF), which is the degradation of the signal-to-noise ratio caused by components in a signal chain. The NF measurement is based on a cold source technique for improved accuracy. Various levels of match and fixture correction are available for additional enhancement. VectorStar is the only VNA platform offering a Noise Figure option enabling NF measurements from 70 kHz to 125 GHz. It is also the only VNA platform available with an optimized noise receiver for measurements from 30 to 125 GHz. 1. NF Overview 1.1. NF Definition 1.2. Importance of Accurate NF Measurements 2. NF Measurement Methods 2.1. Y-Factor / Hot-Cold Noise Figure Measurement Method 2.2. Cold-Source Noise Figure Measurement Method 3. NF Measurement Process 3.1. Test Preparation / Setup 3.2. Instrument Setup 3.3. Measurement Procedure 4. Measurement Example 5. Uncertainties 5.1. Uncertainty Calculator 6. Calculation Example 7. Measurement Tips and Considerations 8. References / Additional Resources 1. NF Overview 1.1 NF Definition Noise figure is a figure-of-merit that describes the degradation of signal-to-noise ratio (SNR) due to added output noise power (No) of a device or system when presented with thermal noise at the input at standard noise temperature (T0, typically 290 K). For amplifiers, the concept can be readily seen. Ideally, when a noiseless input signal is applied to an amplifier, the output signal is simply the input multiplied by the amplifier gain.
    [Show full text]
  • Johnson Noise Thermometry Measurement of the Boltzmann Constant with a 200 Ω Sense Resistor Alessio Pollarolo, Taehee Jeong, Samuel P
    1512 IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, VOL. 62, NO. 6, JUNE 2013 Johnson Noise Thermometry Measurement of the Boltzmann Constant With a 200 Ω Sense Resistor Alessio Pollarolo, Taehee Jeong, Samuel P. Benz, Senior Member, IEEE, and Horst Rogalla, Member, IEEE Abstract—In 2010, the National Institute of Standards and Technology measured the Boltzmann constant k with an electronic technique that measured the Johnson noise of a 100 Ω resistor at the triple point of water and used a voltage waveform synthesized with a quantized voltage noise source (QVNS) as a reference. In this paper, we present measurements of k using a 200 Ω sense re- sistor and an appropriately modified QVNS circuit and waveform. Preliminary results show agreement with the previous value within the statistical uncertainty. An analysis is presented, where the largest source of uncertainty is identified, which is the frequency dependence in the constant term a0 of the two-parameter fit. Index Terms—Boltzmann equation, Josephson junction, mea- surement units, noise measurement, standards, temperature. Fig. 1. Schematic diagram of the Johnson-noise two-channel cross-correlator. I. INTRODUCTION HE Johnson–Nyquist equation (1) defines the thermal measurement electronics are calibrated by using a pseudonoise T noise power (Johnson noise) V 2 of a resistor in a voltage waveform synthesized with the quantized voltage noise bandwidth Δf through its resistance R and its thermodynamic source (QVNS) that acts as a spectral-density reference [8], [9]. temperature T [1], [2]: Fig. 1 shows the experimental schematic. The two chan- nels of the cross-correlator simultaneously amplify, filter, and 2 VR =4kTRΔf.
    [Show full text]
  • Quantum Noise and Quantum Measurement
    Quantum noise and quantum measurement Aashish A. Clerk Department of Physics, McGill University, Montreal, Quebec, Canada H3A 2T8 1 Contents 1 Introduction 1 2 Quantum noise spectral densities: some essential features 2 2.1 Classical noise basics 2 2.2 Quantum noise spectral densities 3 2.3 Brief example: current noise of a quantum point contact 9 2.4 Heisenberg inequality on detector quantum noise 10 3 Quantum limit on QND qubit detection 16 3.1 Measurement rate and dephasing rate 16 3.2 Efficiency ratio 18 3.3 Example: QPC detector 20 3.4 Significance of the quantum limit on QND qubit detection 23 3.5 QND quantum limit beyond linear response 23 4 Quantum limit on linear amplification: the op-amp mode 24 4.1 Weak continuous position detection 24 4.2 A possible correlation-based loophole? 26 4.3 Power gain 27 4.4 Simplifications for a detector with ideal quantum noise and large power gain 30 4.5 Derivation of the quantum limit 30 4.6 Noise temperature 33 4.7 Quantum limit on an \op-amp" style voltage amplifier 33 5 Quantum limit on a linear-amplifier: scattering mode 38 5.1 Caves-Haus formulation of the scattering-mode quantum limit 38 5.2 Bosonic Scattering Description of a Two-Port Amplifier 41 References 50 1 Introduction The fact that quantum mechanics can place restrictions on our ability to make measurements is something we all encounter in our first quantum mechanics class. One is typically presented with the example of the Heisenberg microscope (Heisenberg, 1930), where the position of a particle is measured by scattering light off it.
    [Show full text]
  • Audio Cards for High-Resolution and Economical Electronic Transport Studies
    Audio Cards for High-Resolution and Economical Electronic Transport Studies D. B. Gopman,1 D. Bedau,1, ∗ and A. D. Kent1 1Department of Physics, New York University, New York, NY 10003, USA We report on a technique for determining electronic transport properties using commercially avail- able audio cards. Using a typical 24-bit audio card simultaneously as a sine wave generator and a narrow bandwidth ac voltmeter, we show the spectral purity of the analog-to-digital and digital-to- analog conversion stages, including an effective number of bits greater than 16 and dynamic range better than 110 dB. We present two circuits for transport studies using audio cards: a basic circuit using the analog input to sense the voltage generated across a device due to the signal generated simultaneously by the analog output; and a digitally-compensated bridge to compensate for non- linear behavior of low impedance devices. The basic circuit also functions as a high performance digital lock-in amplifier. We demonstrate the application of an audio card for studying the transport properties of spin-valve nanopillars, a two-terminal device that exhibits Giant Magnetoresistance (GMR) and whose nominal impedance can be switched between two levels by applied magnetic fields and by currents applied by the audio card. Studies of the electronic transport properties of devices ing current-voltage characteristics simultaneously. We and materials require specialized instrumentation. Most will present measurements of magnetic nanostructures, transport studies break down into two classes: current- whose current-voltage and differential resistance are used voltage characterization and differential resistance mea- to determine their underlying magnetic and electronic surements.
    [Show full text]
  • Evolution of the Soundscape Following the Traffic Closure on the Right Bank of the Seine in Paris
    Evolution of the soundscape following the traffic closure on the right bank of the Seine in Paris Fanny Mietlicki Bruitparif, France. Matthieu Sineau Bruitparif, France.. Summary Since September 2016, by decision of the City of Paris, the right bank of the Seine river is closed to traffic along 3.3 km. Bruitparif has put in place a system for assessment of the modifications on the sound environment brought by this closure. This system was based on the implementation of noise measurements at 90 sites in and around Paris as well as modeling. At the end of a year of follow-up, it was possible to establish the following observations: 1. Partial traffic shifts to the lanes located above the banks have generated an increase in traffic noise for residents. This is more pronounced at night (up to 4 dB (A) in some areas) than during the day (less than 2 dB (A) increase). However, during daytime there is an increase of noise peaks (horns, sirens of emergency vehicles ...) related to rising congestion. 2. Other axes in Paris have also undergone a slight increase in noise likely related to the traffic reports, but in a more limited manner (of the order of 1 dB (A)). 3. Outside Paris, especially on the ring road and major roads, no significant change has been noted. 4. At the end of a year of observation, there does not seem to have been an adaptation of the behavior of drivers. 5. On the other hand, traffic noise has clearly decreased on the bank which is now pedestrianized, as well as on the façades of the first buildings located opposite the right banks of the Seine river.
    [Show full text]
  • Noise Figure
    Master Degree (LM) in Electronic Engineering MICROWAVES NOISE AND NON-LINEAR DISTORTION Prof. Luca Perregrini Università di Pavia, Facoltà di Ingegneria [email protected] http://microwave.unipv.it/perregrini/ Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 1 SUMMARY Chapter 10 Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 2 SUMMARY • Dynamic range and sources of noise • Noise power, equivalent noise temperature, measurement of noise temperature • Noise figure of a component and of a cascaded system • Noise figure of a passive two-port network, a mismatched lossy line, a mismatched amplifier • Nonlinear distortion • Gain compression • Harmonic and intermodulation distortion • Third-order intercept point • Intercept point of a cascaded system • Linear and spurious free dynamic range Microwaves, a.a. 2019/20 Prof. Luca Perregrini Noise and non-linear distortion, pag. 3 MOTIVATION Noise is critical to the performance of most RF and microwave communications, radar, and remote sensing systems. Noise determines the threshold for the minimum signal that can be reliably detected by a receiver. Noise power in a receiver will be introduced from the external environment through the receiving antenna, as well as generated internally by the receiver circuitry. The sources of noise in RF and microwave systems, and the characterization of components in terms of noise temperature and noise figure, including the effect of impedance mismatch, will be studied. Compression, harmonic distortion, intermodulation distortion, and dynamic range will also be discussed. These can have important limiting effects when large signal levels are present in mixers, amplifiers, and other components that use nonlinear devices such as diodes and transistors.
    [Show full text]