On the Reciprocal Propelling Powers of Fluids and Certain Rotary Machines Upon Each Other
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
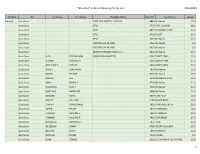
Of Active Mooring Permit List 9/16/2020 1
"Snapshot" of Active Mooring Permit List 9/16/2020 HrbrMstr HID Last Name First Name Business Name Permit# Boat Name Length Record Goat Back - - CAPE COD FROSTY, FLEET #9 4881 No Name 15.0 Goat Back - - KPYC 4737 KPYC LAUNCH 18.0 Goat Back - - KPYC 4822 FLOATING DOCK 24.0 Goat Back - - KPYC 2431 FLOAT 33.0 Goat Back - - KPYC 7526 No Name 31.0 Goat Back - - PISCATAQUA SAILING 7960 No Name 0.0 Goat Back - - PISCATAQUA SAILING 6932 No Name 8.0 Goat Back - - WARPATH FAMILY FARM, INC 6620 No Name 16.0 Goat Back ALEX TED WILLIAM SOUTHEND CHARTERS 6543 THREE SONS 25.0 Goat Back ALLARD RICHARD A 4129 JUDITH ANN 27.0 Goat Back ARSENAULT ERNEST 6410 KAREN ANN 35.0 Goat Back BAILEY JONATHAN 7894 No Name 22.0 Goat Back BAKER STEVEN 8010 No Name 18.0 Goat Back BALLOU LEO 4098 MORNING STAR 25.0 Goat Back BANK SUSAN S. 4734 No Name 22.0 Goat Back BASOUKAS SCOTT 4030 No Name 32.0 Goat Back BOHENKO HARRISON 7990 No Name 14.0 Goat Back BOILARD MARK 4694 CANTALEY 20.0 Goat Back CARLEY WILLIAM 2185 HOUSEBOAT 25.0 Goat Back CARTER RORY DANIEL 7892 ANNA ELIZABETH 38.0 Goat Back CAYER BRUCE 2663 UNKNOWN 26.0 Goat Back CLOUGH MARION E 7619 UNKNOWN 10.0 Goat Back CONNER WILLIAM P 7992 SOPLARME 15.0 Goat Back DANIELSKI MICHAEL C. 7975 TRIO 15.0 Goat Back DE LEEUW JOHN P 4789 GREAT ISLANDER 20.0 Goat Back DELEEW CARLY 7996 No Name 12.0 Goat Back DONLON JAMES 7163 FAMES 9.0 Goat Back DUBE ROBERT 2003 LE CHASSEUR DE CANARD 20.0 1 "Snapshot" of Active Mooring Permit List 9/16/2020 HrbrMstr HID Last Name First Name Business Name Permit# Boat Name Length Record Goat -

On the Cover
VOLUME V /ISSUE 1 JANUARY/FEBRUARY 2007 On the Enjoying A Presque Isle Winter ........ 4 Cover... Presque Isle Bay’s ice is Learning to Love Sailing ........................... 6 another way to love Erie winters like member Stan Zlotkowski “test flying” a Big Girls ..................................................... 8 new locally designed kite called a “YFO” just west of the Club in 2004. What’s An Entson? ................................. 10 Officers Commodore John Murosky........... 456-7797 Recapping the EYCRF Season ............... 18 [email protected] Vice Commodore Dave Arthurs.... 455-3935 [email protected] Basin On The Rise ................................... 22 R/C Dave Amatangelo .................. 452-0010 [email protected] Fleet Captain Tom Trost ............... 490-3363 Personal Watercraft Regulations ...................... 12 [email protected] When I Was A Kid ............................................... 16 Directors P/C James Means ............................... 833-4358 “131 Days To Summer” Party ........................... 20 [email protected] Bob McGee .................................. 838-6551 Yachtswomen of the Year ................................... 26 [email protected] Gerry Urbaniak ............................ 454-4456 Gail Garren Award ............................................. 28 [email protected] CONTENTS CONTENTS CONTENTS CONTENTS CONTENTS Bradley Enterline....................... 453-5004 [email protected] Sam “Rusty” Miller .................... 725-5331 [email protected] Greg Gorny -

NS14 ASSOCIATION NATIONAL BOAT REGISTER Sail No. Hull
NS14 ASSOCIATION NATIONAL BOAT REGISTER Boat Current Previous Previous Previous Previous Previous Original Sail No. Hull Type Name Owner Club State Status MG Name Owner Club Name Owner Club Name Owner Club Name Owner Club Name Owner Club Name Owner Allocated Measured Sails 2070 Midnight Midnight Hour Monty Lang NSC NSW Raced Midnight Hour Bernard Parker CSC Midnight Hour Bernard Parker 4/03/2019 1/03/2019 Barracouta 2069 Midnight Under The Influence Bernard Parker CSC NSW Raced 434 Under The Influence Bernard Parker 4/03/2019 10/01/2019 Short 2068 Midnight Smashed Bernard Parker CSC NSW Raced 436 Smashed Bernard Parker 4/03/2019 10/01/2019 Short 2067 Tiger Barra Neil Tasker CSC NSW Raced 444 Barra Neil Tasker 13/12/2018 24/10/2018 Barracouta 2066 Tequila 99 Dire Straits David Bedding GSC NSW Raced 338 Dire Straits (ex Xanadu) David Bedding 28/07/2018 Barracouta 2065 Moondance Cat In The Hat Frans Bienfeldt CHYC NSW Raced 435 Cat In The Hat Frans Bienfeldt 27/02/2018 27/02/2018 Mid Coast 2064 Tiger Nth Degree Peter Rivers GSC NSW Raced 416 Nth Degree Peter Rivers 13/12/2017 2/11/2013 Herrick/Mid Coast 2063 Tiger Lambordinghy Mark Bieder PHOSC NSW Raced Lambordinghy Mark Bieder 6/06/2017 16/08/2017 Barracouta 2062 Tiger Risky Too NSW Raced Ross Hansen GSC NSW Ask Siri Ian Ritchie BYRA Ask Siri Ian Ritchie 31/12/2016 Barracouta 2061 Tiger Viva La Vida Darren Eggins MPYC TAS Raced Rosie Richard Reatti BYRA Richard Reatti 13/12/2016 Truflo 2060 Tiger Skinny Love Alexis Poole BSYC SA Raced Skinny Love Alexis Poole 15/11/2016 20/11/2016 Barracouta -

1 Guide for Race Committee to Ensure Accurate Results and Posting to the GNS Website in a Timely Manner
Page 1 of 6 To be completed by Race Committee Officer (RCO) Name: Tel: eMail: Date: Series: Race: Course: 1 or 2 Wind & Direction TIME Conditions R C O 1 Guide for Race Committee to ensure accurate results and posting to the GNS website in a timely manner. These notes are provided to give clarity to those volunteers who may not be familiar with the sailboat scoring process. Please read carefully. 1. All boats that wish to be scored should have a current SYLVRA Handicap. 2. Ensure that the SAIL NUMBER is captured accurately and the fleet that the boat wishes to compete in ‐(Note: A PHRF boat that wishes to compete 'White Sail' ‐ this should be reflected in the NOTES section below so the correct handicap can be applied in SailWave.) 3. The BOAT TYPE should also be entered. 4. To simplify the scoring process ALL times are based on TIME of DAY (TOD) This should be taken from either the Race Committee's watch or where applicable the large clock on the committee boat. Ensure each fleet 'START TIMES' are entered on SCORE SHEET 5. Best practice is that 2 people fill in separate SCORE SHEETS. This provides a back‐up copy should there be any discrepancy. 6. ALL completed sheet making up this package: this cover page, the participants and the results for the race should be handed over to the individual club score person to be entered into SailWave and posted to the GNS Racing website. Any duplicate SCORE SHEETs should also be returned. (Can use Table below for check‐in for Laser 28 Fleet) SAIL # BOAT TYPE (Laser 28) NOTES 1 2 3 4 5 6 7 8 9 10 2 PRE‐RACE CHECK‐IN. -

Cruising Copper Harbor of Lake Superior
Volume XVIII No. 5 June 2007 CruisingCruising CopperCopper HarborHarbor ofof LakeLake SuperiorSuperior BoatBoat Smart:Smart: MakeMake thethe TransmissionTransmission CountCount ChicagoChicago MacMac PreviewPreview Over 500 New and Used Boats S A I L I N G S C H O O L Safe, fun, learning Learn to sail on Three Metro Lakes; Also Leech Lake, MN; Pewaukee Lake, WI; School of Lake Superior, Apostle Islands, Bayfield, WI; Lake Michigan; Caribbean Islands the Year On-the-water courses weekends, week days, evenings starting May: Gold Standard • Basic Small Boat - $195 • Basic Keelboat - ASA Certification • Basic Coastal Cruising - ASA Certification • Coastal Navigation • Bareboat Charter - ASA Certification • Advanced Coastal Cruising - ASA Offshore Courses • Vacation Courses: Combined Basic Cruising and Bareboat Charter 4-day live aboard courses on Lake Superior in the Beautiful Apostle Islands and Lake Michigan • Family Vacation Courses and Adventures From 3 To 5 Days • Cruising Multihull Aboard 38’ Catamaran • Celestial • Radar • Weather • Women’s Only Courses (All Levels): Call to set yours up or join others Newsletter • Rides • Call For Private, Flexible Schedule • Youth Sailing Camp (See P. 47) 763-542-9707 Northern Breezes Sailing School www.NorthernBreezesSchool.com 3949 Winnetka Ave. N., Minneapolis, MN 55427 www.SailingBreezes.com Carefree Sailing Twin Cities Dealer for Catalina Yachts 26-50' Join our 2007 Sail Club starting at $795 00 !! And captain/skipper 22-26' Catalinas • Lake Minnetonka sailing • Non-Sailor? ASA Sailing School -

Our Thirtieth Ye
Our Thirtieth Yea r w w w.lymanmorse.com • 207-354-6904 HOB NOB - Seguin 44 HODIMAR L to R:Rod Stephens,Cabot, BLUE DOLPHIN – Don Kipp Hull #1 Russ Goldsmith Goldsmiths Th i rt y Yea r s of Bui l d i n g In 1978 the old Morse Boat- from Neil Bond and Frank Simon cruising boats in history and building Company was closing, we started development and we were proud to be part of it. but when I approached Roger planning for the Lyman-Morse Hinckley, Cambria, Little Harbor Morse about renting the old Seguin 44 series. and Alden were all successfully building I found that he had Fortunately, we hit the mar- building high-end 44’s that were already contracted with Clayton ket at just the right time as the all exceptionally well rounded Ewing and Porter Schutt cruiser/racers. to finish their Jarvis Although the plan ”The era starting from Newman 46 hulls using was for Neil and Frank that facility. With Roger’s to build a 44 for them- the late 70’s to the encouragement I contact- selves, they never did, ed Clayton and Porter to but given their faith in discuss my plans, and us, as well as financial mid 80’s produced with agreement from all support, we were still parties proceeded to pur- able to launch the chase the land and build- project. Our hard work some of the finest ings, and assume the con- soon paid off when tracts to build DYNA and Mitch Neff from EGRET. -

Straphanger (10 Points If You Know Where That Name Came From!) and Press Releases
EST 1941 July 2020 Edition July 2020 Commodore’s Comment Well the season got off with a bang, perhaps not a huge bang but a worthwhile one all the same. It was pleasing to see such a roll-up for the Trophy Presentation. Thank-you to all concerned. Congratulations to those who won trophies, and I must say that, as dancers we make much better sailors! Well done, Maria! We are certainly enjoying beautiful Queensland weather at the moment, and it was picture perfect for the first racing of the season, as it was last Saturday. Much better than sailing colleagues have down south. Speaking of ‘down south’, most of you would have heard by now, the news that the Cruising Yacht Club of Australia, the most prestigious yacht club in Australia, has had to implement their full Covid response plan. It is a timely reminder that, although here in our area we seem to be relatively “safe” and clear of the virus, we do not need complacency when it comes to our own Covid Safety Plan. All members are responsible to maintain vigilance with COVID-19 safe practices such as social distancing, good hand hygiene and to monitor for symptoms. If you have symptoms or feel un-well, please do not attend events. I realise that this type of safety measure is foreign to us all however, those of us who attend work places, cafes, bars, restaurants, and other community social gathering areas, have all experienced Covid safety plans. It is no different for our Club. We cannot fail also, to support the management of The Gladstone Yacht Club, our leasee, in these endeavours. -

2020 October Bay Breeze
Bay Breeze October 2020 http://www.escanabayachtclub.com/ The Escanaba Yacht Club Clubhouse will be closed and locked for the season by mid-October. Thanks to Dan Branson, Cindy Anthony and Bob Rosenfeldt for their time and expertise to winterize the Clubhouse. Finances: Oct 12, 2020 Checking $3155.74 Building Fund $6,637.30 The 2 rentals this season, managed by Roxanne Branson, earned $600 for the Building Fund which is used to make necessary repairs and improvements to the Clubhouse. There were 2 additional cancellations due to the Coronavirus, and 1 reservation for 2021. During the colder months, EYC meetings are planned for the second MONDAY of November – April, 7PM, as a ZOOM meeting, until conventional “around the table” meetings can be held. All members are welcome to attend. The EYC welcomes the new Harbormaster, Shayne Sanville, with a big thank you to Larry Gravatt for his “11 years of leadership with unwavering dedication to the harbor, boats & boat owners, EYC members and visitors”. Halloween Party is cancelled. The Annual Banquet at the Terrace Ballroom, usually scheduled for the coldest night in January, has been cancelled due to the Coronavirus pandemic. The EYC Board will be assessing the Coronavirus situation, and hopes to schedule an Annual Banquet & Meeting in the spring. The Election of Officers and Directors ballots will be mailed to members, the returns compiled and the results will be published along with a 2021 EYC Calendar and List of Officers and Directors. 2020 Race Results are posted on the EYC website: http://escanabayachtclub.com/racing.html Considering the constraints on social gathering, the EYC sailing competition went smoothly, on some really lovely sailing days – and a few cold windy days. -

Transfer Waiting List
Transfer Waiting List For your convenience, we have published our new applicant waiting list and our transfer list. The lists are sorted by date. To find your position on the list, simply reference the month, day and year in which you applied. New applicants and transfers are assigned based on application date, preference and availability. Please read the “Procedure for Assigning Seasonal Mooring Permits” in the Rules and Regulations section to see the order of assignments as dictated by the code of the Chicago Park District. The assignment process for transfers and new applicants is now a year round process. They can be conducted anywhere from a weekly to a monthly basis depending on availability, time of year, outstanding transfers and outstanding applications. The greatest availability occurs after the deadline for seasonal renewals, when non-renewed spaces become available. Transfers within harbors are done before transfers between harbors and there may be several rounds of each. Applications are done after the completion of the transfer rounds. All transfer requests will remain on file until they are accommodated. If you wish to cancel a request, you must notify us in writing. Also be aware that if you have multiple transfer requests and one of them is accommodated, the other transfer requests will remain active unless you cancel them by notifying us in writing. If you contact us regarding a transfer, please refer to it by the date of the transfer, not the number listing. These numbers are simply the order at the time the list is printed and change as people receive or withdraw transfers. -

2015 Sailboat Race Book and Sailing Program Information
Seattle Yacht Club Established in 1892 2015 Sailboat Race Book and Sailing Program Information Glory – Seattle Yacht Club 2014 Sailboat of the Year Seattle Yacht Club Sailboat Race Book and Sailing Program Information 1807 East Hamlin Street Seattle, Washington 98112 www.seattleyachtclub.org SYC Front Desk 206.325.1000 Sailing Office 206.926.1011 Sailing Office Fax 206.324.8784 Table of Contents Welcome to the 2015 Sailing Season ........................................................................................................ 1 Sailboat Activity Calendar............................................................................................................................. 3 Race Registration Procedure ....................................................................................................................... 4 Registration Checklist .................................................................................................................................... 5 SYC Sailboat Racing Program ...................................................................................................................... 6 Overview of Sailboat Racing Events .................................................................................................... 6 SYC Notice of Race Addendum .............................................................................................................. 8 Puget Sound Sailboat Safety Regulations ....................................................................................... 10 -

Annals Section4 Yachts.Pdf
CHAPTER 4 Early Yachts IN THE R.V.Y.C. FROM 1903 TO ABOUT 1933 The following list of the first sail yachts in the Club cannot be said to be complete, nevertheless it provides a record of the better known vessels and was compiled from newspaper files of The Province, News-Advertiser, The World and The Sun during the first three decades of the Club activities. Vancouver newspapers gave very complete coverage of sailing events in that period when yacht racing commanded wide public interest. ABEGWEIT—32 ft. aux. Columbia River centerboard cruising sloop built at Steveston in 1912 for H. C. Shaw, who joined the Club in 1911. ADANAC-18 ft. sloop designed and built by Horace Stone in 1910. ADDIE—27 ft. open catboat sloop built in 1902 for Bert Austin at Vancouver Shipyard by William Watt, the first yacht constructed at the yard. Addie was in the original R.V.Y.C. fleet. ADELPIII—44 ft. schooner designed by E. B. Schock for Thicke brothers. Built 1912, sailed by the Thicke brothers till 1919 when sold to Bert Austin, who sold it in 1922 to Seattle. AILSA 1-28.5 ft. D class aux. yawl, Mower design. Built 1907 by Bob Granger, originally named Ta-Meri. Subsequent owners included Ron Maitland, Tom Ramsay, Alan Leckie, Bill Ball and N. S. McDonald. AILSA II—22.5 ft. D class aux. yawl built 1911 by Bob Granger. Owners included J. H. Willard and Joe Wilkinson. ALEXANDRA-45 ft. sloop designed for R.V.Y.C. syndicate by William Fyfe of Fairlie, Scotland and built 1907 by Wm. -

February – March
BMW Sydney, Rushcutters Bay. The legs you see in this picture be ong to John. His job is to make sure when you drive away after a service at BMW Sydney, your car looks as good as the day you drove it off the showroom floor. And we can honestly say, when it comes to detail, no one is as driven as John. Of course, he's not alone. He's only one of five staff dedicated to this sole task. And obviously, we do mean dedicated. It's quite selfish really, but we've always believed that if you look good, so do we. From the way we service your car to the way we serve you a coffee while you wait, it's what makes BMW Sydney a world of BMW. BMW Sydney, 65 Craigend Street, Rushcutters Bay. 9334 4555. www.bmwsydney.com.au 1999 Telstra Sydney to Hobart A TIME TO REMEMBER 4 In the fastest race in 55 years, the Volvo 60 Nokia, a Danish/Australian entry, slashed the record for the Telstra Sydney to Hobart Yacht Race while 15 other yachts also broke Morning Glory's time. YES TO YENDYS 8 IMS Overall winner of the 1999 Telstra Sydney to Hobart, the Farr 49 Yendys, had raced for only nine days , including the Hobart, when she crossed the line on the Derwent River to clinch victory for owner/skipper Geoffrey Ross. TAILENDING THE FLEET 12 The story of the race aboard the 22-year-old 33-footer Berrimilla, the last yacht to complete the race to Hobart, taking seven days 10 hours and logging 920 nautical miles for the rhumbline course of 630 mile.