DOCSLIB.ORG

Rigidity of Quasiconformal Maps on Carnot Groups

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Rigidity of Quasiconformal Maps on Carnot Groups RIGIDITY OF QUASICONFORMAL MAPS ON CARNOT GROUPS Mark Medwid A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY August 2017 Committee: Xiangdong Xie, Advisor Alexander Tarnovsky, Graduate Faculty Representative Mihai Staic Juan Bes´ Copyright c August 2017 Mark Medwid All rights reserved iii ABSTRACT Xiangdong Xie, Advisor Quasiconformal mappings were first utilized by Grotzsch¨ in the 1920’s and then later named by Ahlfors in the 1930’s. The conformal mappings one studies in complex analysis are locally angle-preserving: they map infinitesimal balls to infinitesimal balls. Quasiconformal mappings, on the other hand, map infinitesimal balls to infinitesimal ellipsoids of a uniformly bounded ec- centricity. The theory of quasiconformal mappings is well-developed and studied. For example, quasiconformal mappings on Euclidean space are almost-everywhere differentiable. A result due to Pansu in 1989 illustrated that quasiconformal mappings on Carnot groups are almost-everywhere (Pansu) differentiable, as well. It is easy to show that a biLipschitz map is quasiconformal but the converse does not hold, in general. There are many instances, however, where globally defined quasiconformal mappings on Carnot groups are biLipschitz. In this paper we show that, under cer- tain conditions, a quasiconformal mapping defined on an open subset of a Carnot group is locally biLipschitz. This result is motivated by rigidity results in geometry (for example, the theorem by Mostow in 1968). Along the way we develop background material on geometric group theory and show its connection to quasiconformal mappings. iv ACKNOWLEDGMENTS I would like to acknowledge, first and foremost, my wife, Heather. She’s put up with the long nights and anxiety that accompany graduate school; she constantly cheered me on, told me to be more confident, and agreed to put her life on hold for a number of years while I finished my degree. I’m not sure my finishing graduate school would be possible without her support. Next, I would like to thank my advisor, Xiangdong Xie, who exposed me to a new field of mathematics. He very patiently put up with my na¨ıve questions, ignorance and incorrect proofs; he slowly helped me to become a better mathematician. Beyond academics, he gave me lots of helpful career and life advice that I’ll be sure to apply in the future. He is also one of the first people to encourage me to graduate early – this lead to me accepting a new tenure-track job. I would also like to acknowledge and thank the other members of my dissertation commit- tee (Mihai Staic, Juan Bes´ and Alexander Tarnovsky) for their thoughtful commentary on my manuscript and insightful questions during my defense. Furthermore, I would like to acknowledge my fellow colleagues (both former and present) for their many helpful discussions on life, graduate school and mathematics. I formed many valuable friendships during graduate school. There are too many to be included here, but I will attempt to do so: Jake Laubacher, David Walmsley, Todd Romutis, John Haman and Sam Carolus shared an office with me and kept my day-to-day life more interesting. This was a room filled with exceedingly promising young mathematicians and I was honored to be a part of it. I’d also like to thank Robert Kelvey, Jeff Norton and Leo Pinheiro (who are all now on to greener pastures) for their many helpful conversations with me. My family, in particular, my parents, deserve special mention for all their support over the ten consecutive years I’ve been in school since graduating from high school in 2007. They’ve always had my back, no matter what. Finally, I feel that the Math & Stats Department at BGSU deserves special mention. The department supported my education expenses and my livelihood, and there are so many stellar faculty and staff members that helped form me both as a mathematician and as a teacher. v TABLE OF CONTENTS Page CHAPTER 1 INTRODUCTION . 1 1.1 The Word Metric . 2 1.2 Quasi-Isometries . 3 1.3 Quasi-Isometric Rigidity . 9 CHAPTER 2 PRELIMINARIES . 11 2.1 BiLipschitz Mappings . 11 2.2 Quasiconformality . 12 2.3 Quasisymmetric Mappings . 17 CHAPTER 3 QUASI-ISOMETRIES ON HYPERBOLIC SPACE . 24 3.1 The Morse Lemma . 24 3.2 The Gromov Boundary . 35 CHAPTER 4 CARNOT GROUPS . 42 4.1 Lie Algebras and Lie Groups . 42 4.2 The Exponential Map & Carnot-Caratheodory´ Distance . 46 4.3 Pansu’s Differentiation Theorem . 51 CHAPTER 5 MAIN RESULTS . 55 5.1 Rigidity of Quasisymmetric Mappings on Fibered Metric Spaces . 55 5.2 Rigidity of Quasiconformal Maps on Two-Step Carnot Groups . 66 BIBLIOGRAPHY . 76 vi LIST OF FIGURES Figure Page 2.1 An artist’s rendering of what a quasiconformal map might look like. 13 3.1 The Morse Lemma. 25 3.2 Two cases for triangles in trees. 31 3.3 Asymptotic rays in the upper-half plane model of H2. 36 1 CHAPTER 1 INTRODUCTION The purpose of this dissertation is to develop the theory accompanying the main result of the author’s research efforts while studying at Bowling Green State University, as well as the proof of the result itself. The author assumes knowledge of basic group theory, analysis, and point-set topology; anything beyond this will be developed in the pages contained hereafter. The following is the author’s main result: Theorem. Let G = V1 V2 be a two-step Carnot group and let W1 V1 be a subspace and set ⊕ ✓ W := [W ,W ]. Let W = W W ; W is a Lie sub-algebra of G and so corresponds to a Lie 2 1 1 1 ⊕ 2 subgroup. Suppose that E G is an open set. If f : E G is a quasiconformal mapping that ✓ ! permutes the left cosets of W , then f is locally biLipschitz. Many of the terms contained in the above theorem are ostensibly foreign to the reader. The basic idea is the following: Carnot groups are spaces that are “nice” enough to carry some notion of differentiability. The definition is fairly similar in flavor to the familiar one from calculus. One then becomes interested in a certain type of (almost everywhere) differentiable function f that we name “quasiconformal.” As in calculus, f needs only to be defined on an open subset for the purposes of the theorem. If f moves a particular subset in a nice enough way, then it turns out that f is locally biLipschitz – to wit, inside a smaller open set, f distorts distances by no more than some bounded factor. This is perhaps enough to remind one of the famed Mean Value Theorem of first year calculus: Theorem. Let f :[a, b] R be continuous and differentiable on (a, b). Then there exists some ! number c in (a, b) so that f(b) f(a) = f 0(c) (b a). | − | · − When f has a bounded derivative, then this implies f distorts the lengths of intervals by a bounded factor. The main result of this dissertation is, of course, different in many ways from the 2 Mean Value Theorem, requiring a different setting and assumptions, but the punchline to this quick corollary carries a similar spirit. With the above context, the main theorem is an analysis theorem. However, the study of such theorems also has some deep ties to the world of geometric group theory that will be fleshed out in the body of the dissertation. While quasiconformal analysis is used in several branches of math- ematics, it is through geometric group theory that the author was first exposed to the study of quasiconformal mappings. Details for theorems and definitions will be provided (when useful) so as to make this dissertation a stand-alone document for the readers; however, the introductory material is, for the most part, well studied. Many excellent papers and books exist for provid- ing copious details on these subjects – recommendations will be provided when relevant for the interested reader. 1.1 The Word Metric Recall that a group is finitely generated if there exists a finite set S so that G = S . In what h i follows, unless specified, G denotes a finitely generated group. One can endow G with a metric space structure as follows. Definition 1.1.1. (Kapovich, 2013) Suppose that G is a finitely generated group with generating set S = s1,s2,...,sd . The Cayley graph of G with respect to S is a graph Γ(G, S) with vertex { } set G and edges are constructed according to the rule there is an edge connecting g and h g = h s✏ for some 1 i d, ✏ 1, 1 . () · i 2{− } Definition 1.1.2. (Kapovich, 2013) Let G be a finitely generated group with generating set S, and suppose Γ(G, S) is the Cayley graph of G with respect to S. Endow Γ with the shortest path metric d – the restriction of d to G, dS, is called the word metric on G with respect to S and is denoted (G, dS). One should note that, if e is the identity element of G, then for any g G, d (e, g) is 2 S the reduced word length of g with letters in S. Suppose h, g G; write both h and g as re- 2 3 ✏ ✏ ✏ ✏ duced words with letters in S, i.e. h = s 1h s kh ,g = s 1g s kg . Then the sequence i(1h) ··· i(kh) i(1g) ··· i(kg) ✏1g ✏1g ✏kg 1 (h, hs ,...,hs s − ,hg) h hg i(1g) i(1g) i(kg 1) gives an edge-path joining and , so this implies that ··· − d(e, g) d(h, hg).
Load more

Recommended publications
  • Casimir Functions of Free Nilpotent Lie Groups of Steps Three and Four
    Casimir functions of free nilpotent Lie groups of steps three and four∗ A. V. Podobryaev A.K. Ailamazyan Program Systems Institute of RAS [email protected] June 2, 2020 Abstract Any free nilpotent Lie algebra is determined by its rank and step. We consider free nilpotent Lie algebras of steps 3, 4 and corresponding connected and simply connected Lie groups. We construct Casimir functions of such groups, i.e., invariants of the coadjoint representation. For free 3-step nilpotent Lie groups we get a full description of coadjoint orbits. It turns out that general coadjoint orbits are affine subspaces, and special coadjoint orbits are affine subspaces or direct products of nonsingular quadrics. The knowledge of Casimir functions is useful for investigation of integration properties of dynamical systems and optimal control problems on Carnot groups. In particular, for some wide class of time-optimal problems on 3-step free Carnot groups we conclude that extremal controls corresponding to two-dimensional coad- joint orbits have the same behavior as in time-optimal problems on the Heisenberg group or on the Engel group. Keywords: free Carnot group, coadjoint orbits, Casimir functions, integration, geometric control theory, sub-Riemannian geometry, sub-Finsler geometry. AMS subject classification: 22E25, 17B08, 53C17, 35R03. Introduction The goal of this paper is a description of Casimir functions and coadjoint orbits for arXiv:2006.00224v1 [math.DG] 30 May 2020 some class of nilpotent Lie groups. This knowledge is important for the theory of left- invariant optimal control problems on Lie groups [1]. Casimir functions are integrals of the Hamiltonian system of Pontryagin maximum principle.
    [Show full text]
  • Non-Minimality of Corners in Subriemannian Geometry
    NON-MINIMALITY OF CORNERS IN SUBRIEMANNIAN GEOMETRY EERO HAKAVUORI AND ENRICO LE DONNE Abstract. We give a short solution to one of the main open problems in subrie- mannian geometry. Namely, we prove that length minimizers do not have corner- type singularities. With this result we solve Problem II of Agrachev's list, and provide the first general result toward the 30-year-old open problem of regularity of subriemannian geodesics. Contents 1. Introduction 1 1.1. The idea of the argument 2 1.2. Definitions 3 2. Preliminary lemmas 4 3. The main result 6 3.1. Reduction to Carnot groups 6 3.2. The inductive non-minimality argument 7 References 9 1. Introduction One of the major open problems in subriemannian geometry is the regularity of length-minimizing curves (see [Mon02, Section 10.1] and [Mon14b, Section 4]). This problem has been open since the work of Strichartz [Str86, Str89] and Hamenst¨adt [Ham90]. Contrary to Riemannian geometry, where it is well known that all length minimizers are C1-smooth, the problem in the subriemannian case is significantly more difficult. The primary reason for this difficulty is the existence of abnormal curves (see [AS04, Date: March 8, 2016. 2010 Mathematics Subject Classification. 53C17, 49K21, 28A75. Key words and phrases. Corner-type singularities, geodesics, sub-Riemannian geometry, Carnot groups, regularity of length minimizers. 1 2 EERO HAKAVUORI AND ENRICO LE DONNE ABB15]), which we know may be length minimizers since the work of Montgomery [Mon94]. Nowadays, many more abnormal length minimizers are known [BH93, LS94, LS95, GK95, Sus96]. Abnormal curves, when parametrized by arc-length, need only have Lipschitz- regularity (see [LDLMV14, Section 5]), which is why, a priori, no further regular- ity can be assumed from an arbitrary length minimizer in a subriemannian space.
    [Show full text]
  • Measure Contraction Properties of Carnot Groups Luca Rizzi
    Measure contraction properties of Carnot groups Luca Rizzi To cite this version: Luca Rizzi. Measure contraction properties of Carnot groups . Calculus of Variations and Partial Differential Equations, Springer Verlag, 2016, 10.1007/s00526-016-1002-y. hal-01218376v3 HAL Id: hal-01218376 https://hal.archives-ouvertes.fr/hal-01218376v3 Submitted on 21 May 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. MEASURE CONTRACTION PROPERTIES OF CARNOT GROUPS RIZZI LUCA Abstract. We prove that any corank 1 Carnot group of dimension k + 1 equipped with a left-invariant measure satisfies the MCP(K, N) if and only if K ≤ 0 and N ≥ k + 3. This generalizes the well known result by Juillet for the Heisenberg group Hk+1 to a larger class of structures, which admit non-trivial abnormal minimizing curves. The number k + 3 coincides with the geodesic dimension of the Carnot group, which we define here for a general metric space. We discuss some of its properties, and its relation with the curvature exponent (the least N such that the MCP(0,N) is satisfied). We prove that, on a metric measure space, the curvature exponent is always larger than the geodesic dimension which, in turn, is larger than the Hausdorff one.
    [Show full text]
  • On Logarithmic Sobolev Inequalities for the Heat Kernel on The
    ON LOGARITHMIC SOBOLEV INEQUALITIES FOR THE HEAT KERNEL ON THE HEISENBERG GROUP MICHEL BONNEFONT, DJALIL CHAFAÏ, AND RONAN HERRY Abstract. In this note, we derive a new logarithmic Sobolev inequality for the heat kernel on the Heisenberg group. The proof is inspired from the historical method of Leonard Gross with the Central Limit Theorem for a random walk. Here the non commutative nature of the increments produces a new gradient which naturally involves a Brownian bridge on the Heisenberg group. This new inequality contains the optimal logarithmic Sobolev inequality for the Gaussian distribution in two dimensions. We compare this new inequality with the sub- elliptic logarithmic Sobolev inequality of Hong-Quan Li and with the more recent inequality of Fabrice Baudoin and Nicola Garofalo obtained using a generalized curvature criterion. Finally, we extend this inequality to the case of homogeneous Carnot groups of rank two. Résumé. Dans cette note, nous obtenons une inégalité de Sobolev logarithmique nouvelle pour le noyau de la chaleur sur le groupe de Heisenberg. La preuve est inspirée de la méthode historique de Leonard Gross à base de théorème limite central pour une marche aléatoire. Ici la nature non commutative des incréments produit un nouveau gradient qui fait intervenir naturellement un pont brownien sur le groupe de Heisenberg. Cette nouvelle inégalité contient l’inégalité de Sobolev logarithmique optimale pour la mesure gaussienne en deux dimensions. Nous comparons cette nouvelle inégalité avec l’inégalité sous-elliptique de Hong-Quan Li et avec les inégalités plus récentes de Fabrice Beaudoin et Nicola Garofalo obtenues avec un critère de courbure généralisé.
    [Show full text]
  • Conformal and Cr Mappings on Carnot Groups
    PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY, SERIES B Volume 7, Pages 67–81 (June 17, 2020) https://doi.org/10.1090/bproc/48 CONFORMAL AND CR MAPPINGS ON CARNOT GROUPS MICHAEL G. COWLING, JI LI, ALESSANDRO OTTAZZI, AND QINGYAN WU (Communicated by Jeremy Tyson) Abstract. We consider a class of stratified groups with a CR structure and a compatible control distance. For these Lie groups we show that the space of conformal maps coincide with the space of CR and anti-CR diffeomorphisms. Furthermore, we prove that on products of such groups, all CR and anti-CR maps are product maps, up to a permutation isomorphism, and affine in each component. As examples, we consider free groups on two generators, and show that these admit very simple polynomial embeddings in CN that induce their CR structure. 1. Introduction In this article, we consider the interplay between metric and complex geometry on some model manifolds. This is the first outcome of a larger project which aims to develop a unified theory of conformal and CR structures on the one hand, and to define explicit polynomial embeddings of certain CR manifolds into Cn on the other. This kind of embedding is what permits the detailed analysis of the ∂b operator carried out by Stein and his collaborators since the 1970s (see [6]). The analogy between CR and conformal geometry is well documented in the case of CR manifolds of hypersurface-type, see, e.g., [7,10–14,17]. The easiest and perhaps the most studied example in this setting is that of the Heisenberg group, taken with its sub-Riemannian structure.
    [Show full text]
  • Arxiv:1604.08579V1 [Math.MG] 28 Apr 2016 ..Caatrztoso I Groups Lie of Characterizations 5.1
    A PRIMER ON CARNOT GROUPS: HOMOGENOUS GROUPS, CC SPACES, AND REGULARITY OF THEIR ISOMETRIES ENRICO LE DONNE Abstract. Carnot groups are distinguished spaces that are rich of structure: they are those Lie groups equipped with a path distance that is invariant by left-translations of the group and admit automorphisms that are dilations with respect to the distance. We present the basic theory of Carnot groups together with several remarks. We consider them as special cases of graded groups and as homogeneous metric spaces. We discuss the regularity of isometries in the general case of Carnot-Carathéodory spaces and of nilpotent metric Lie groups. Contents 0. Prototypical examples 4 1. Stratifications 6 1.1. Definitions 6 1.2. Uniqueness of stratifications 10 2. Metric groups 11 2.1. Abelian groups 12 2.2. Heisenberg group 12 2.3. Carnot groups 12 2.4. Carnot-Carathéodory spaces 12 2.5. Continuity of homogeneous distances 13 3. Limits of Riemannian manifolds 13 arXiv:1604.08579v1 [math.MG] 28 Apr 2016 3.1. Tangents to CC-spaces: Mitchell Theorem 14 3.2. Asymptotic cones of nilmanifolds 14 4. Isometrically homogeneous geodesic manifolds 15 4.1. Homogeneous metric spaces 15 4.2. Berestovskii’s characterization 15 5. A metric characterization of Carnot groups 16 5.1. Characterizations of Lie groups 16 Date: April 29, 2016. 2010 Mathematics Subject Classification. 53C17, 43A80, 22E25, 22F30, 14M17. This essay is a survey written for a summer school on metric spaces. 1 2 ENRICO LE DONNE 5.2. A metric characterization of Carnot groups 17 6. Isometries of metric groups 17 6.1.
    [Show full text]
  • A Maximum Principle in the Engel Group James Klinedinst University of South Florida, [email protected]
    University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School 4-4-2014 A Maximum Principle in the Engel Group James Klinedinst University of South Florida, [email protected] Follow this and additional works at: https://scholarcommons.usf.edu/etd Part of the Mathematics Commons Scholar Commons Citation Klinedinst, James, "A Maximum Principle in the Engel Group" (2014). Graduate Theses and Dissertations. https://scholarcommons.usf.edu/etd/5248 This Thesis is brought to you for free and open access by the Graduate School at Scholar Commons. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. A Maximum Principle in the Engel Group by James Klinedinst A thesis submitted in partial fulfillment of the requirements for the degree of Master of Arts Department of Mathematics & Statistics College of Arts and Sciences University of South Florida Major Professor: Thomas Bieske, Ph.D. Razvan Teodorescu, Ph.D. Seung-Yeop Lee, Ph.D. Date of Approval: April 04, 2014 Keywords: Viscosity Solutions, Partial Differential Equations, Carnot Groups, Heisenberg Group Copyright c 2014, James Klinedinst Dedication This work is dedicated to my son, Blaise. May his discov- eries be even better. Table of Contents Abstract . ii Chapter 1 Background on the Engel Environment . 1 Chapter 2 Carnot Jets and Viscosity Solutions . 10 Chapter 3 Sub-Riemannian Maximum Principle . 14 References . 26 i Abstract In this thesis, we will examine the properties of subelliptic jets in the Engel group of step 3. Step-2 groups, such as the Heisenberg group, do not provide insight into the general abstract calculations.
    [Show full text]
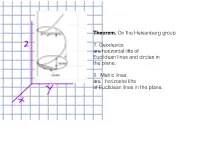
  • Heisenberg Copy Theorem. on the Heisenberg Group 1. Geodesics Are
    Theorem. On the Heisenberg group Z 1. Geodesics are horizontal lifts of Euclidean lines and circles in the plane. heisenberg copy 2. Metric lines are horizontal lifts of Euclidean lines in the plane. Y x 3 as a manifold: R as a metric space: x Call a smooth path c(t) = (x(t), y(t),dyed z(t)) ``horizontal’’ if : dz 1 dx dy = (x(t) O y(t) O) dt 2 dt − dt and call the length of such a path : b dx 2 dy 2 `(c):= dx2 + dy2 := + dt c a s dt dt Z p Z Then d(A, B) = inf { length of c: c horizontal, c joins A to B } as a Lie group: (x,y,z)(x’, y’, z’) = (x + x’, y+ y’, z+ z’) + (0,0, (1/2)(xy’ - yx’)) d is a left-invariant metric on the Heisenberg group: d(gA, gB) = d(A, B) The projection 3 2 ⇡ : R R ; ⇡(x, y, z)=(x, y) ! is a submetry: DEF: a submetry is an onto map F between metric spaces such that F(B(p, r)) = B(F (p ), r) `(c)=` 2 (⇡(c)) = ⇡ is a submetry R ) center 0,921 horn spaces t f I c h8 IT r R2 c is the horizontal lift of γ γ(t)=(x(t),y(t)) = c(t)=(x(t),y(t),z(t)) where ) dz 1 dy dx = (x(t) y(t) ) dt 2 dt − dt Theorem. On the Heisenberg group Z 1. Geodesics are horizontal lifts of Euclidean lines and circles in the plane.
    [Show full text]
  • A Primer on Carnot Groups
    Anal. Geom. Metr. Spaces 2017; 5:116–137 Survey Paper Open Access Enrico Le Donne* A Primer on Carnot Groups: Homogenous Groups, Carnot-Carathéodory Spaces, and Regularity of Their Isometries https://doi.org/10.1515/agms-2017-0007 Received November 18, 2016; revised September 7, 2017; accepted November 8, 2017 Abstract: Carnot groups are distinguished spaces that are rich of structure: they are those Lie groups equipped with a path distance that is invariant by left-translations of the group and admit automorphisms that are dilations with respect to the distance. We present the basic theory of Carnot groups together with several remarks. We consider them as special cases of graded groups and as homogeneous metric spaces. We discuss the regularity of isometries in the general case of Carnot-Carathéodory spaces and of nilpotent metric Lie groups. Keywords: Carnot groups, sub-Riemannian geometry, sub-Finsler geometry, homogeneous spaces, homoge- neous groups, nilpotent groups, metric groups MSC: 53C17, 43A80, 22E25, 22F30, 14M17. Carnot groups are special cases of Carnot-Carathéodory spaces associated with a system of bracket-generating vector elds. In particular, they are geodesic metric spaces. Carnot groups are also examples of homogeneous groups and stratied groups. They are simply connected nilpotent groups and their Lie algebras admit special gradings: stratications. The stratication can be used to dene a left-invariant metric on each group in such a way that the group is self-similar with respect to this metric. Namely, there is a natural family of dilations on the group under which the metric behaves like the Euclidean metric under Euclidean dilations.
    [Show full text]
  • NILPOTENT GROUPS WITHOUT EXACTLY POLYNOMIAL DEHN FUNCTION 3 Suitable Subspace
    NILPOTENT GROUPS WITHOUT EXACTLY POLYNOMIAL DEHN FUNCTION STEFAN WENGER Abstract. We prove super-quadratic lower bounds for the growth of the filling area func- tion of a certain class of Carnot groups. This class contains groups for which it is known that their Dehn function grows no faster than n2 log n. We therefore obtain the existence of (finitely generated) nilpotent groups whose Dehn functions do not have exactly polynomial growth and we thus answer a well-known question about the possible growth rate of Dehn functions of nilpotent groups. 1. Introduction Dehn functions have played an important role in geometric group theory. They measure the complexity of the word problem in a given finitely presented group and provide a quasi- isometry invariant of the group. A class of groups for which the Dehn function has been well-studied is that of nilpotent groups. Many results on upper bounds for the growth of the Dehn function are known, while fewer techniques have been found for obtaining lower bounds. Here are some known results: if Γ is a finitely generated nilpotent group of step c c+1 c+1 then its Dehn function δΓ(n) grows no faster than n , in short δΓ(n) n , [12, 20, 9]. If c+1 Γ is a free nilpotent group of step c then δΓ(n) ∼ n , [5, 21]. This includes the particular case of the first Heisenberg group, which was known before, see [8]. For the definition of δΓ(n) and the meaning of and ∼ see Section 2. The higher Heisenberg groups have quadratic Dehn functions, [12, 1, 16].
    [Show full text]
  • Spectral Triples on Carnot Manifolds
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Institutionelles Repositorium der Leibniz Universität Hannover Spectral Triples on Carnot Manifolds Von der Fakult¨atf¨ur Mathematik und Physik der Gottfried Wilhelm Leibniz Universit¨atHannover zur Erlangung des Grades Doktor der Naturwissenschaften Dr. rer. nat. genehmigte Dissertation von Dipl.Math. Stefan Hasselmann geboren am 12.04.1981 in Ibbenb¨uren 2014 ii Referent: Prof. Dr. Christian B¨ar Koreferent: Prof. Dr. Elmar Schrohe Tag der Promotion: 18.10.2013 Abstract We analyze whether one can construct a spectral triple for a Carnot manifold M, which detects its Carnot-Carath´eodory metric and its graded dimension. Therefore we construct self-adjoint horizontal Dirac operators DH and show that each horizontal Dirac operator detects the metric via Connes' formula, but we also find that in no case these operators are hypoelliptic, which means they fail to have a compact resolvent. First we consider an example on compact Carnot nilmanifolds in detail, where we present a construction for a horizontal Dirac operator arising via pullback from the Dirac operator on the torus. Following an approach by Christian B¨arto decompose the horizontal Clifford bundle, we detect that this operator has an infinite dimensional kernel. But in spite of this, in the case of Heisenberg nilmanifolds we will be able to discover the graded dimension from the asymptotic behavior of the eigenvalues of this horizontal Dirac operator. Afterwards we turn to the general case, showing that any horizontal Dirac operator fails to be hypoelliptic. Doing this, we develop a criterion from which hypoellipticity of certain graded differential operators can be excluded by considering the situation on a Heisenberg manifold, for which a complete characterization of hypoellipticity in known by the Rockland condition.
    [Show full text]
  • Large Time Behavior for the Heat Equation on Carnot Groups
    Nonlinear Differ. Equ. Appl. Nonlinear Differential Equations c 2012 Springer Basel DOI 10.1007/s00030-012-0215-9 and Applications NoDEA Large time behavior for the heat equation on Carnot groups Francesco Rossi Abstract. We first generalize a decomposition of functions on Carnot groups as linear combinations of the Dirac delta and some of its deriv- atives, where the weights are the moments of the function. We then use the decomposition to describe the large time behavior of solutions of the hypoelliptic heat equation on Carnot groups. The solution is decom- posed as a weighted sum of the hypoelliptic fundamental kernel and its derivatives, the coefficients being the moments of the initial datum. Mathematics Subject Classification (2000). Primary 35R03; Secondary 35H10, 58J37. Keywords. Hypoelliptic operators, Carnot groups, Heat equations. 1. Introduction The study of Carnot groups and of PDEs on these spaces have drawn an increasing attention for several reasons. First, Carnot groups are topologically extremely simple, since they are isomorphic to RN , but in the same time their metric structure is different, since they are naturally endowed with Carnot– Caratheodory metrics. Second, several tangent spaces to Carnot–Caratheodory metric spaces are diffeomorphic to Carnot groups. Third, and more connected to PDEs, Carnot groups are the easiest examples of spaces where hypoelliptic equations are naturally defined (see [4] and references therein). Thus, they are the most natural examples in which one can study relations between the solutions of the hypoelliptic PDEs and the Carnot–Caratheodory metrics. With this goal, we first generalize a decomposition of functions first stated in [7] for functions on RN .
    [Show full text]