DOCSLIB.ORG

Oftimiation of Water Resources Master of Science

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Oftimiation of Water Resources Master of Science Optimization of water resources for irrigation in Dinajpur and Rangpur, East Pakistan. Item Type Thesis-Reproduction (electronic); text Authors Karim, Muhammad Abdul,1940- Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 02/10/2021 10:56:42 Link to Item http://hdl.handle.net/10150/191493 OFTIMIATION OF WATER RESOURCES FOR IRRIGATION IN DINAJPUR AND RANGPUR, EAST PAKISTAN by Muhammad A. Karim A Thesis Submitted to the Faculty of the CONNITTEE ON HYDROLOGY AND WATER RESOURCES In Partial Fulfillment of the Requirements For the Degree of MASTER OF SCIENCE In the Graduate College THE UNIVERSITY OF ARIZONA 1968 STATEMEN'r BY AUTHOR This thesis has been submitted in partial fulfill- ment of requirements for an advanced degree at The Univer- sity of Arizona and is deposited in the University Library to be made available to borrowers under rules of the Library. Brief quotations from this thesis are allowable without special permission, provided that accurate acknowledgment of source is made. Requests for permis- sion for extended quotation from or reproduction of this manuscript in whole or in part may be granted by the head of the major department or the Dean of the Graduate Col- lege when in his judgment the proposed use of thematerial is in the interests of scholarship. In all other instances, however, permission must be obtained from the author. SIGD 4n APPROVAL BY THESIS DIRECTOR This thesis has been approved on the date shown below: EUGEHE S. SIIVIIPSON Professor of Hydrology AC KNO WI FUDGMENIS The author is greatly indebted to Dr. Eugene S. Simpson, thesis director, for his valuable suggestions and guidance in accomplishing this task. Special thanks are due to the Personnel of the International Engineering Company, Inc., and the Direc- torate of Hydrology, East Pakistan Water and Power Development Authority, Dacca, East Pakistan, for com- pilation of hydrologic data as needed for this study. The author is grateful to Dr. Daniel D. Evans, Chairman of the Committee on Hydrology and Water Resources, and to Dr. Jerome J. Wright for their guidance and encouragement. The author is indebted to East Pakistan Water and Power Development Authority, and the United Nations Food and Agriculture Organization for providing the opportunity and facilities for training the author in hydrology. 111 TABLE OF CONTEN'IS Page LIST OF TABLES vi LIST OF ILLUSTRATIONS viii ABSTRACT ix CHABTER I IWDRODUCTION 1 II GENTRAL DESCRIPTION OF THE AREA 4 Location 4 Topography and Drainage 4 Soils 6 Geology 6 Climate and Hydrology 7 Available Surface Water for Irrigation 11 Available Ground Water Storage . 13 III AQUIFER CHARACTERISTICS AND PERFORMANCE OF TUE WELL 16 Kozeny Method 17 Hantush Method 20 Kraijenhoff Method 22 Performance of Wells 26 Ill FUTURE CROP AND IRRIGATION NEEDS 32 Need for Irrigation 32 Irrigation Water Requirements 32 iv V Page V T EFFECT OF A WELL ON THE FLOW OF A ]NEAREY STREAM 44 VI ECONOMIC SPACING OF WELLS 51 VII ECONOMY OF DEEP WELLS VIII SUMMARY AND CONCLUSIONS 60 REFERENCES 63 LIST OF TABLES Table Page 1 General Characteristics of the Material Penetrated in the Drillings 8 2 Mean Monthly Rainfall for Dinajpur, East Pakistan,1900-1962 9 3 Mean Monthly Rainfall for Rangpur, East Pakistan,1900-1960 10 Summary Results of Computing Evapotranspira- tion and Water Balance - after Thornthwaite and Mather(1957) 15 5 Transmissivity by Kozeny Method 20 6 Transmissivity by Hantush Method(196)4) 23 7 Transmissivity by Kraijenhoff Method(1958) 26 8 Summary Results of Transmissivity and Stor- age Coefficient of Aquifer 27 9 Suggested Future Cropping Patterns in Dinajpur and Rangpur Districts, East Pakistan 33 10 Monthly Consumptive Use Dinajpur and Rangpur Districts, East Pakistan 36 11 Consumptive Use of Water for the Suggested Future Crops after Blaney-Criddle(1966) for 100 Acres of Farm Land in Dinajpur and Rangpur, East Pakistan 37 12 Consumptive Use Based on Thornthwaite(19)48) in Dinajpur and Rangpur Districts, East Pakistan 38 vi vii Table Page 13 Future Agriculture Production in the Project Area 42 Expected Annual Income and Benefits in the Project Area (per 100 Acres) )43 15 Estimated Annual Cost per Acre in Ground 5)4 Water Irrigation Project Dinajpur . 16 Estimated Annual Cost of Items for380 Tubewells in Dinajpur Districts 55 LIST OF ILLUSTRATIONS Figure Page 1 Location Map of East Pakistan 2 2 Location Map of Groundwater Projects, Dinajpur and Rangpur Districts S 3 A. Hydrograph of Karatoa(1963-196)4) B. Hydrograph of Tangon(1962-1963). 12 Ease Discharge of Tangon River versus Time 25 5 Graph for Determining Potential Evapotrans- piration after Thornthwaite(19)48) . 39 6 Rainfall and Irrigation Demand (based on 90%dry year and land use) after Blaney- Criddle(1966) 7 Graph for Determining the Portion of Well- Discharge Furnished by a Nearby River after Glover and Balmer(195)4) 8 Graph for Determining the Portion of Well- Discharge Furnished by a Nearby River after Hantush(196)4) )49 viii ABSTRACT An area of about 300,000 acres in Dinajpur and Rangpur districts will be irrigated by the combination of pumpage from the Tangon and Karatoa rivers and from about 1000 wells located between the rivers. It was calculated that the lowering of the water table 12-15 feet, as needed for irrigation, due to pumpage from the underground will stop or severely limit the accretion to the stream flow from underground. The Tangon will, in absence of accretion to the stream from the underground, cease to flow during the irrigation season. Likewise the flow of Karatoa, in absence of accretion to the stream from the underground will be reduced to about 153 cfs which can be used to irrigate 15,000 acres along the banks of rivers only. The average discharge of 2.5 cfs over a 150-day interval of wells located 3000 feet apart will not exceed the average annual recharge of 2.8 feet to the aquifer from precipitation. This particular arrangement was examined from the relationship of aquifer characteristics - trans- missivity 120,000 gpd/ft and the storage coefficient0.20. The resulting calculated benefit-cost ratio of thebenefit ix x of crops produced from assured irrigation to the cost of construction of wells275feet deep is2:1. If the average aquifer properties remain constant at depths greater than275feet, better economy will result by drilling wells deeper than275feet. CHAPTER I INR0DUCTI0N Iring between2005!arid 26°)Q!north latitude and88° 03 and92°)40' east longitude, East Pakistan is a major part of the Ganges-Bhramaputra-Megna delta which is roughly twice the size of. the Mississippi delta, Fig. 1. With about 1,000 people per square mile, the area has one of the densest rural populations in the world. The climate is characterized by a wet season from June to October when average precipitation totals about 70 inches, and a dry season from November to February when precipitation totals about3inches. The months of March through May have a total rainfall of about 10 0 0 inches but temperature averages90F to95F; conse- quently these months have the greatest moisture deficiency. Until recent years, little or no attempt was made to irrigate during the dry months and the fields remained barren. A program is now underway to provide irrigation water from wells and streams wherever possible. Since many streams go dry from March toMay, the main dependence for irrigation water is on wells. Even for the perennial streams, only run-of--the-river water is available, since 1 2 GENERAL MAP INTERNATIONAL BOUNDARY '- ' ---- DISTRICT BOUNDARY RIVERS AND STREAMS IMPORTANT CITIES STUDY AREA SCALE .0 20 50 MILES BOGRA SYLHET MYMENSINGH R A.J S H AH I MEGIIN FAR I D PUR GA RA I S JESSORE KHULNA THE GA OF COX'S BAZAR BEN F BA'? Figure 1.Location Map of East Pakistan 3 the country is too fiat to construct dams. On the other hand, the reserve of subsurface water is very large since the alluvium is thousands of feet thick (maximum thick- ness unknown). The development of the ground water basin constitutes the most important means to attain optimum utilization of the available water resources. It is anticipated that up to 300,000 acres of land will be irri- gated in this area by a combination of pumpage from the Tangon and Karatoa rivers and from about 1,000 wells situated between the rivers. Since stream discharge is supported by effluent seepage, there undoubtedly will be a lessening of stream flow when the wells are pumped. This effect on stream flow will be most severe near the end of the irrigation period when stream flow is lowest and the demand is highest. This creates a unique prob- lem: how best to supply a sufficient quantity of water at all points of the system, at the time of the greatest demand. This, in turn, demands full knowledge of the operational characteristics and capabilities of the under- ground reservoir and its relationship with the surface storage. CHAPTER II GENIRAL DESCRIPTION OF THE AREA Location The area to be irrigated by the pumpage from the underground reservoir and possibly pumpage from the stream is shown in Fig. 2. This area is relatively high and most of it is denied irrigation water from streams because of its loca- tion beyond the reach of the surface diversion. Topography and Drainage The area consists largely of the piedmont plain built up by alluvial fan deposits originating in the foothills of the Himalayas, and carried by the rivers Teesta, Karatoa and their tributaries.
Load more

Recommended publications
  • Download the Full Paper
    Int. J. Biosci. 2021 International Journal of Biosciences | IJB | ISSN: 2220-6655 (Print) 2222-5234 (Online) http://www.innspub.net Vol. 18, No. 4, p. 164-172, 2021 RESEARCH PAPER OPEN ACCESS Livelihood status and vulnerabilities of small scale Fishermen around the Padma River of Rajshahi District Rubaiya Pervin*1, Mousumi Sarker Chhanda2, Sabina Yeasmin1, Kaniz Fatema1, Nipa Gupta2 1Department of Fisheries Management, Hajee Mohammad Danesh Science and Technology University, Dinajpur, Bangladesh 2Depatment of Aquaculture, Hajee Mohammad Danesh Science and Technology University, Dinajpur, Bangladesh Key words: Padma River, Livelihood status, Fishermen, Constraints, Suggestions http://dx.doi.org/10.12692/ijb/18.4.164-172 Article published on April 30, 2021 Abstract The investigation was conducted on the livelihood status of small scale fishermen around the Padma river in Rajshahi district from July 2016 to February 2017. Hundred fishermen were surveyed randomly with a structured questionnaire. The livelihood status of fishermen was studied in terms of age, family, occupation, education, housing and health condition, credit and income. It was found that most of the fishermen were belonged to the age groups of 20-35 years (50%) represented by 85% Muslims. Majority of them (62%) lived in joint family and average household size was 6-7 people. Educational status revealed that 66% were illiterate. Fishermen houses were found to be of two types namely semi-constructed and unconstructed and among them 77% houses were connected with electricity. About 85% fishermen were landless represented by 95% rearing livestock. Regarding health and sanitation 85% fishermen used sanitary latrines. About 83% fishermen were solely depends on fishing and annual income of 50% fishermen was 50,000 to 60,000 TK.
    [Show full text]
  • Spatial Study of Mahananda Basin in the Geo - Historical Perspective
    © 2020 JETIR May 2020, Volume 7, Issue 5 www.jetir.org (ISSN-2349-5162) SPATIAL STUDY OF MAHANANDA BASIN IN THE GEO - HISTORICAL PERSPECTIVE DHARMENDRA KUMAR1, PRAVIN KUMAR2, RAVINDRA SHRIVASTAVA 3 1. RESEARCH SCHOLAR, DEPT. OF HISTORY, B. N. MANDAL UNIVERSITY, MADHEPURA-852113, BIHAR, INDIA 2. RESEARCH SCHOLAR, DEPT. OF GEOGRAPHY, B. N. MANDAL UNIVERSITY, MADHEPURA-852113, BIHAR, INDIA 3. RESEARCH SCHOLAR, DEPT. OF ZOOLOGY, B. N. MANDAL UNIVERSITY, MADHEPURA-852113, BIHAR, INDIA Karatoa tathatreyee Louhityascha Mahanandah, Shalmali Gomati chaiba Sandhya Trlsrota sa tatha' (Mhabharat,sabhaparba,Ch.9/22-23) Mahananda has been a notable river since the ancient period . At present there are so many literary and archaeological evidence available like in Mahabharata, Acharangsutra, Kalpsutra etc. It is a tributary of the mighty river Ganga, Mahananda river rises from springs in the Dow Hills forest also known as Mahanadi in the Darjeeling hills originating from the Mahaldiram range Hill near Chimli, east of Kurseong in Darjeeling district at an elevation of 2,100 meters (6,900 ft). Actually Mahanadi and Balasan are the two rivers that meet together to form Mahananda river in the plain of Siliguri sub-division. There is a confusion about the source of Mahananda. Among the two above mentioned rivers, the Balasan has been originated from Lepcha Jagat ( 2360.6m ) and Mahanadi from Mahaldiram ( 2250m). From the stand point of elevation Balasan has been flowing from higher elevation than that of the Mahanadi. That’s why Balasan should be the source river of Mahananda. And Mahanadi is its tributary. Actually the Mahananda River is a trans-boundary river which originates in the Himalayas.
    [Show full text]
  • National Water Management Plan Approved
    National Water Management Plan Approved The National Water Management Plan (NWMP), prepared question to determine on the basis of practical experience, by WARPO under the supervision of the Ministry of Water current knowledge and capacity. All projects will adhere to Resources has been approved by the National Water normal Government administrative procedures and will conform Resources Council (NWRC) headed by the honorable Prime to all relevant rules and guidelines issued by the Government. Minister of the People's Republic of Bangladesh. The The National Water Management Plan is structured in a manner approval was given at the seventh meeting of the Council that enables the objectives of the 84 different programmes held on March 31, 2004. It was decided in the meeting that planned for the next 25 years to contribute individually and WARPO will centrally monitor and coordinate the collectively in attaining both the overall objectives as well as the implementation of NWMP. intermediate sub-sectoral goals. The programmes are grouped NWMP is a framework plan consisting of 84 programmes. into eight sub-sectoral clusters and spatially distributed across These programmes are to be implemented by the line eight planning regions of the country. Information on each, agencies and others as designated. Each organization is together with a wide range of planning data, is contained in the responsible for planning and implementing its own activities National Water Resources Database, accessible through an and projects within the NWMP framework. 35 agencies have information management system. There are three main been identified for implementing the programmes of NWMP categories of programmes in the NWMP, namely, Cross-cutting in independent, lead and supporting capacities.
    [Show full text]
  • MACH-II Completion Report – Volume- 2 MACH Performance Monitoring
    MACH-II Completion Report – Volume- 2 MACH Performance Monitoring Baikka Beel Permanent Sanctuary, Hail Haor June, 2007 A project of the Government of Bangladesh Supported by USAID Project Partners: Winrock International Bangladesh Centre for Advanced Studies (BCAS) Center for Natural Resource Studies (CNRS) CARITAS Bangladesh MACH-II Completion Report Volume-II June 2007 Winrock International Bangladesh Centre for Advanced Studies Center for Natural Resource Studies CARITAS Bangladesh Table of Contents Preface SO 6 Indicators Summary Sheet Revised Result Framework Tab-1 Indicator 6.a Extent to which best practices from USAID projects are used elsewhere Tab-2 Indicator 6.b Maintaining or increasing Fish production of natural resources in targeted area (kg/ha/year) Increase in wetland and riparian trees Tab-3 Indicator 6.c Maintaining or increasing biodiversity Tab-4 Indicator 6.1a Area of floodplain where sustainable management is implemented. Tab-5 Indicator 6.2a Aquatic habitats converted from seasonal to perennial in targeted Areas (ha). Tab-6 Indicator 6.2b Riparian habitat improved in targeted areas.(km) Tab-7 Indicator 6.2.1a Number of new sanctuaries established Tab-8 Indicator 6.2.1b Number of wetland/riparian trees successfully established Tab-9 Indicator 6.2.2a Average annual increase in targeted individual RUG member supplemental income (Tk) Tab-10 Indicator 6.2.2b Number of RUG fishers having reduced effort Tab-11 Indicator 6.2.2c Total number of AIG loans Tab-12 Indicator 6.3a Number of water bodies leased to community resource management groups in targeted areas. Tab-13 Indicator 6.3b Number of communities adopting the following key regulation in target areas.
    [Show full text]
  • Integration of Satellite Image Derived Temperature and Water Depth for Assessing Fish Habitability in Dam Controlled Flood Plain Wetland
    Integration of Satellite Image Derived Temperature and Water Depth for Assessing Fish Habitability in Dam Controlled Flood Plain Wetland Sonali Kundu University of Gour Banga Swades Pal ( [email protected] ) University of Gour Banga https://orcid.org/0000-0003-4561-2783 Swapan Talukdar University of Gour Banga Susanta Mahato University of Gour Banga Pankaj Singha University of Gour Banga Research Article Keywords: Wetland, damming effect, Fish habitat, Depth niche, Thermal gradient, Consistency of thermally conducive habitat Posted Date: July 26th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-675840/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License 1 Integration of satellite image derived temperature and water depth for 2 assessing fish habitability in dam controlled flood plain wetland 3 Sonali Kundu1, Swades Pal1*, Swapan Talukdar1, Susanta Mahato1, Pankaj Singha1 4 1 Department of Geography, University of Gour Banga, Malda, India. 5 *Corresponding author ([email protected]) 6 Abstract 7 The present study attempted to investigate the changes in temperature conducive to fish 8 habitability during the summer months in a hydrologically modified wetland following damming 9 over a river. Satellite image-driven temperature and depth data calibrated with field data were 10 used to analyse fish habitability and the presence of thermally optimum habitable zones in some 11 fishes such as Labeo Rohita, Cirrhinus mrigala, Tilapia fish, Small shrimp, and Cat fishes. The 12 study was conducted both at the water's surface and at the optimum depth of survival. It is very 13 obvious from the analysis that a larger part of wetland has become an area that destroyed aquatic 14 habitat during the post-dam period and existing wetlands have suffered significant shallowing of 15 water depth.
    [Show full text]
  • Image Driven Hydrological Components Based Fish Habitability Modeling in Riparian Wetlands Triggered by Damming
    Image Driven Hydrological Components Based Fish Habitability Modeling in Riparian Wetlands Triggered by Damming Swades Pal University of Gour Banga Rumki Khatun ( [email protected] ) University of Gour Banga Research Article Keywords: Damming, Hydrological modication, Fishing habitat suitability, Rule based decision tree model and Hydrological components Posted Date: July 26th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-651761/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/19 Abstract Assessing sh habitability in pursuance of damming for some selected shes in wetland of Indo- Bangladesh barind tract using hydrological ingredients like hydro-period, water depth, and water presence consistency is major focus of the present study. Rule based decision tree modeling has been applied for integrating aforesaid hydrological parameters to nd out habitat suitability for some selected shes like carp shes, shrimps, tilapia and cat shes both for pre-dam and post-dam periods. From this work it is highlighted that damming has accelerated the rate of wetland deterioration in forms of hydrological ow alteration i.e. inconsistency in water presence has increased, hydro-duration became shortened and water depth has attenuated. From the model it is very clear that a small proportion area was considered to be good sh habitat (16.54–39.90%) in pre-dam period, but after damming almost all parts have become least suitable for sh habitability. Field survey has conrmed that shing quantity, growing rate of shes was higher in pre-dam situation but it is reduced gradually during post-dam period.
    [Show full text]
  • A Two-Day International Webinar Organized by Department of Geography University of Gour Banga on 24-25Th September, 2020
    Programme schedule of A two-day International Webinar Organized by Department of Geography University of Gour Banga On 24-25th September, 2020 Day-1 (24.09.2020) Inaugural Session (10:00 am – 10:45 am) Date Time Inaugural Session Google Meet link: https://meet.google.com/fdg-svkv-bbg 24.09.2020 10:00 am – 10:45 am Welcome Address by Convener Inaugural Address by Hon’ble Vice Chancellor, UGB Special speech by Respected Registrar, UGB Vote of thanks Day-1 (24.09.2020) Plenary Session-1 (11:00 am -12:10 pm) Google Meet link: https://meet.google.com/fdg-svkv-bbg Date Time Resource Person Topic 24.09.2020 11:00 am - Distinguished Professor Biswajeet Spatial Intelligence for 11:35am Pradhan Natural Hazard Director, Centre for Advanced Modelling Assessment and Geospatial Information Systems (CAMGIS), School of Information, Systems & Modelling Faculty of Engineering and IT University of Technology Sydney, Australia 11:35 am - Professor Pawan Kumar Joshi Geoinformatics for 12:10pm Chairperson – Special Centre for Disaster Contemporary Research Environmental Issues Professor – School of Environmental Sciences Jawaharlal Nehru University, New Delhi 110 067 Plenary Session-2 (12:15 pm-1:30 pm) Google Meet link: https://meet.google.com/fdg-svkv-bbg Date Time Resource Person Topic 24.09.2020 12:15 pm Prof. Malay Mukhopadhyay Landscape Sustainability: -12:45 Professor, Department of Geography A New Dimension in pm Visva Bharati, Santiniketan Environmental Research India, PIN-7321235 12:45 – Professor Atiqur Rahman Water Resource 1:15 pm Professor, Urban Environmental & Remote Challenges in the Sensing Division Urbanized World Department of Geography, Faculty of Natural Sciences Jamia Millia Islamia, New Delhi-25 (India) Launch break (1:15pm-2:00pm) Plenary Session-3 (2:00pm-2:35pm) Google Meet link: https://meet.google.com/fdg-svkv-bbg 2:00pm- Prof.
    [Show full text]
  • Here We Are Born
    REFUGEE UNSETTLED AS I ROAM: MY ENDLESS SEARCH FOR A HOME AZMAT ASHRAF Suite 300 - 990 Fort St Victoria, BC, V8V 3K2 Canada www.friesenpress.com Copyright © 2020 by Azmat Ashraf First Edition — 2020 Cover Photo by David Marcu on Unsplash All rights reserved. No part of this publication may be reproduced in any form, or by any means, electronic or mechanical, including photocopying, recording, or any information browsing, storage, or retrieval system, without permission in writing from FriesenPress. ISBN 978-1-5255-6382-9 (Hardcover) 978-1-5255-6383-6 (Paperback) 978-1-5255-6384-3 (eBook) 1. biography & autobiography, personal memoirs Distributed to the trade by The Ingram Book Company A true story of a family’s search for a home over three generations, told by one family member, in his own words. Dedicated to the courage and resilience of millions of refugees around the world. TABLE OF CONTENTS Foreword ................................................................................ VII SIXTH MIGRATION ...................................................................... 1 BIRTH OF A REFUGEE ................................................................. 13 FIRST MIGRATION ....................................................................... 23 To the Land of Opportunity ......................................................... 23 The Innocent Sixties ................................................................. 35 The Maghreb Rule .................................................................... 41 The First True Friend ...............................................................
    [Show full text]
  • Annual Flood Report 2017
    ANNUAL FLOOD REPORT 2017 FLOOD FORECASTING & WARNING CENTER PROCESSING & FLOOD FORECASTING CIRCLE BANGLADESH WATER DEVELOPMENT BOARD TABLE OF CONTENTS TABLE OF CONTENTS................................................................................................................. 2 LIST OF TABLES ........................................................................................................................... 3 LIST OF FIGURE ............................................................................................................................ 5 PREFACE ......................................................................................................................................... 7 EXECUTIVE SUMMARY .............................................................................................................. 9 LIST OF ABBREVIATIONS ...................................................................................................... 10 CHAPTER 1: INTRODUCTION ............................................................................................... 12 1.1. THE PHYSICAL SETTING ................................................................................................................... 12 1.2. THE RIVER SYSTEM .......................................................................................................................... 12 1.3. ACTIVITIES OF FFWC ....................................................................................................................... 14 1.4. OPERATIONAL STAGES
    [Show full text]
  • Annual Flood Report 2019
    ANNUAL FLOOD REPORT 2019 FLOOD FORECASTING & WARNING CENTRE PROCESSING & FLOOD FORECASTING CIRCLE BANGLADESH WATER DEVELOPMENT BOARD Annual Flood Report 2019 Flood Forecasting and Warning Centre (FFWC) Bangladesh Water Development Board (BWDB) WAPDA Building (8th Floor), Motijheel C/A, Dhaka-1000 Phone : 9550755; 9553118 Fax : 9557386 Email ; [email protected] ; [email protected] Web : www.ffwc.gov.bd Editing & Compilation: Md. Arifuzzaman Bhuyan, Executive Engineer, FFWC, BWDB Sarder Udoy Raihan, Sub-Divisional Engineer, FFWC, BWDB Contribution: Md. Alraji Leon, Assistant Engineer, FFWC, BWDB Partho Protim Barua, Assistant Engineer, FFWC, BWDB Preetom Kumar Sarker, Assistant Engineer, FFWC, BWDB Mehadi Hasan, Assistant Engineer, FFWC, BWDB Review: Md. Saiful Hossain, Superintending Engineer, PFFC, BWDB Published by the FFWC, BWDB, Ministry of Water Resources, Dhaka TABLE OF CONTENTS LIST OF TABLES .......................................................................................................................... 5 LIST OF FIGURES ........................................................................................................................ 7 PREFACE ..................................................................................................................................... 10 EXECUTIVE SUMMARY .......................................................................................................... 12 LIST OF ABBREVIATIONS ....................................................................................................
    [Show full text]
  • CM Launches Web-Portal to Gets Closure to People
    CMYK Friday, August 2, 2013 The Arun Information 3 Vol - II Issue - 29 Friday, August 2, 2013 Naharlagun Read online at www.arunachalipr.gov.in News Flash Poor connectivity & Itanagar Treasury office CM launches web-portal shifted infrastructures pose NAHARLAGUN: The Itanagar Treasury office has been shifted to to gets closure to people serious problems in the first floor of the newly constructed office building of the Directorate of Accounts and Treasuries, Goernment development of AP : of Arunachal Pradesh, Bank Tinali, Itanagar with effect from July 29 last. Governor Ph.D awarded NAHARLAGUN: As per the provision under ordinance No 25 & 26 of the Rajiv Gandhi University and on the basis of the satisfactory reports of the examiners and viva-voce board held on July 18 last, Ms. Momme Mesia, on the thesis “Land system Inventory for Environment Appraisal: A case study of Charju River Basin, Purvanchal Hills, Arunachal Pradesh” and Mr. Anmal Saikia, on the thesis “ A study ITANAGAR, July 28: the Public Grievances Redressal citizens, know your CM, opinion poll, on Geomorphology and Hydrological State Chief Minister Nabam Tuki has Cell in the website. The website has RSS feed subscription and social Aspects of Borgang River basin, the formally launched the Chief Minister’s a page dedicated especially for the media integration like Facebook, Eastern Himalaya” are declared to web portal – arunachalpradesh.cm.in grievances and complaints. Twitter etc. KOLKATA, July 28: China has done in Tibet. He said that have qualified for the award of the at the CM’s conference hall here The objective of the portal is The website www.arunachal Arunachal Pradesh Governor Lt.
    [Show full text]
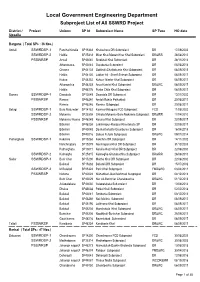
  • Subproject List by District (All)
    Local Government Engineering Department Subproject List of All SSWRD Project District / Project Unions SP Id Subproject Name SP Type HO date Upazila Barguna ( Total SPs : 36 Nos.) Amtali SSWRDSP-1 Pancha Koralia SP15333 Khatachora DR Subproject DR 17/09/2002 SSWRDSP-2 Haldia SP25318 Mirar Khal-Magan Khar Khal Subproject DR&IRR 28/04/2010 PSSWRSP Amtali SP43040 Singkhali Khal Subproject DR 28/11/2013 Atharogasia. SP43044 Garabunia Subproject DR 04/06/2014 Chawra SP44103 Gotkhali-Chalitabunia Khal Subproject DR 08/09/2015 Haldia SP44120 Jabbar Ali - Sharif Shimon Subproject DR 06/09/2017 Kukua SP46252 Kukua- Nimter Khal Subproject DR 06/09/2017 Athargachia SP46253 Arua-Kamini Khal Subproject DR&WC 06/09/2017 Haldia SP46276 Purba Chila Khal Subproject DR 06/09/2017 Bamna SSWRDSP-1 Dawatala SP13049 Dawatala DR Subproject DR 12/01/2002 PSSWRSP Ramna SP46240 Amtoli Ruhita Potkakhali DR 20/06/2017 Ramna SP46246 Ramna Subproject DR 20/06/2017 Betagi SSWRDSP-1 Bura Majumder SP14182 Kawnia-Mirjaganj FCD Subproject FCD 11/08/2002 SSWRDSP-2 Mokamia SP25308 Chhoto Mokamia-Bara Mokamia Subproject DR&IRR 17/04/2010 PSSWRSP Mokamia/ HosnabadSP46245 Koruna Khal Subproject DR 22/05/2017 Bibichini SP46238 Lakshmipur-Ranipur-Khantakata SP DR 22/05/2017 Bibichini SP43048 Deshantarkathi-Gouribunia Subproject DR 16/04/2015 Bibichini SP42016 Gabua Fultala Subproject DR&WC 09/07/2014 Patharghata SSWRDSP-1 Kakchira SP15268 Kakchira DR Subproject DR 14/11/2002 Nanchnapara SP15279 Nachnapara Khal DR Subproject DR 31/12/2003 Patharghata SP13071 Koralia-Hazir Khal
    [Show full text]