DOCSLIB.ORG

NOTES Maxwell’S Equations ( Incomplete So Far)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
NOTES Maxwell’S Equations ( Incomplete So Far) NOTES Maxwell’s Equations ( incomplete so far) Gauss’s law Gauss’ law for magnetism Faraday’s law Ampere’s law Parallel-Plate Capacitor Revisited For surface S , I = I, B=0 ? Not -Q 1 s experimentally! but for surface S2, Is = 0 Q Wait, LHS is the same (because C is the same)! ?? You could make this work if a fictitious current Id is added to Is in such a way that Id is zero for S1 but is equal to I for S2. will work. Displacement Current James Clerk Maxwell proposed that a changing electric field induces a magnetic field, in analogy to Faraday’s law: where a changing magnetic field induces an electric field. Ampere’s law is revised to become Ampere-Maxwell law where is the displacement current. MAXWELL’S EQUATIONS “COMPLETED” Basis for Electromagnetic Waves! The equations are often written in slightly different (and more convenient) forms when dielectric and/or magnetic materials are present. MAXWELLS EQUATIONS James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish theoretical physicist] His most prominent achievement was formulating a set of equations that united previously unrelated observations, experiments, and equations of electricity, magnetism, and optics into a consistent theory. His theory of classical electromagnetism demonstrates that electricity, magnetism and light are all manifestations of the same phenomenon, namely the electromagnetic field. Maxwell's achievements concerning electromagnetism have been called the "second great unification in physics” after the first one realized by Isaac Newton. Maxwell demonstrated that electric and magnetic fields travel through space in the form of waves at the speed of light in 1865, with the publication of A Dynamical Theory of the Electromagnetic Field. Maxwell proposed that light was in fact undulations in the same medium that is the cause of electric and magnetic phenomena. The unification of light and electrical phenomena led to the prediction of the existence of radio waves. TRANSVERSE ELECTROMAGNET WAVE T E M wave NOTES 7B-20 TRANSVERSE ELECTROMAGNETIC WAVE Notation for a TEM wave traveling in the + x direction ( Change + to – for traveling in the – x drection ) Ey = Em sin 2π ( x/λ - t/T ) T=1/f, ω = 2πf Bz = Bm sin 2π ( x/λ – t/T ) k = 2π/λ 2π/λ measures x the longitudinal extension 2π/T = 2πf measures t the time ELECTOMAGNETIC WAVE FARADAY INDUCTION PART Electromagnetic Waves From Faraday’s Law c TRANSVERSE ELECTROMAGNETIC WAVE AMPERE LAW PART Electromagnetic Waves From Ampère’s Law Electric Dipole Radiation Electromagnetic Wave Propagation in Free Space So, again we have a traveling electromagnetic wave speed of light in vacuum Ampere’s Law Faraday’s Law Speed of light in vacuum is currently defined rather than measured (thus defining meter and Wave Equation also the vacuum permittivity). NOTES Plane Electromagnetic Waves where c • Transverse wave • Plane wave (points of given phase form a plane) x • Linearly polarized (fixed plane contains E) Energy Density of Electromagnetic Waves • Electromagnetic waves contain energy. We know already expressions for the energy density stored in E and B fields: EM wave • So Total energy density is Energy Propagation in Electromagnetic Waves Energy flux density equals Energy transmitted through unit time per unit area • Intensity I = Average energy flux density (W/m2) Define Poynting vector Direction is that of wave propagation average magnitude is the intensity Radiation Pressure Electromagnetic waves carry momentum as well as energy. In terms of total energy of a wave U, the momentum is U/c. During a time interval Δt , the energy flux through area A is ΔU =IA Δ t . If radiation is totally absorbed: momentum imparted radiation pressure EXERTED If radiation is totally reflected: x2 Maxwell’s Rainbow Light is an Electromagnetic Wave NOTES Physics 241 - Extra QUIZ 3 An electromagnetic wave is traveling in +x direction and the electric field at a particular point on the x-axis points in the +z direction at a certain instant in time. At this same point and instant, what is the direction of the magnetic field? a) -z z b) -x E c) -y y d) +y e) None of the above x The direction of travel is that of E x B. Physics 241 – Extra QUIZ 3 An electromagnetic wave is traveling through a particular point in space where the direction of the electric field is along the +z direction and that of the magnetic field is along the +y direction at a certain instant in time. Which direction is this wave traveling? z a) +x E b) -x y c) -y B d) -z x The direction of travel e) None of the above is that of E x B. .
Load more

Recommended publications
  • Chapter 16 – Electrostatics-I
    Chapter 16 Electrostatics I Electrostatics – NOT Really Electrodynamics Electric Charge – Some history •Historically people knew of electrostatic effects •Hair attracted to amber rubbed on clothes •People could generate “sparks” •Recorded in ancient Greek history •600 BC Thales of Miletus notes effects •1600 AD - William Gilbert coins Latin term electricus from Greek ηλεκτρον (elektron) – Greek term for Amber •1660 Otto von Guericke – builds electrostatic generator •1675 Robert Boyle – show charge effects work in vacuum •1729 Stephen Gray – discusses insulators and conductors •1730 C. F. du Fay – proposes two types of charges – can cancel •Glass rubbed with silk – glass charged with “vitreous electricity” •Amber rubbed with fur – Amber charged with “resinous electricity” A little more history • 1750 Ben Franklin proposes “vitreous” and “resinous” electricity are the same ‘electricity fluid” under different “pressures” • He labels them “positive” and “negative” electricity • Proposaes “conservation of charge” • June 15 1752(?) Franklin flies kite and “collects” electricity • 1839 Michael Faraday proposes “electricity” is all from two opposite types of “charges” • We call “positive” the charge left on glass rubbed with silk • Today we would say ‘electrons” are rubbed off the glass Torsion Balance • Charles-Augustin de Coulomb - 1777 Used to measure force from electric charges and to measure force from gravity = - - “Hooks law” for fibers (recall F = -kx for springs) General Equation with damping - angle I – moment of inertia C – damping
    [Show full text]
  • APPENDICES 206 Appendices
    AAPPENDICES 206 Appendices CONTENTS A.1 Units 207-208 A.2 Abbreviations 209 SUMMARY A description is given of the units used in this thesis, and a list of frequently used abbreviations with the corresponding term is given. Units Description of units used in this thesis and conversion factors for A.1 transformation into other units The formulas and properties presented in this thesis are reported in atomic units unless explicitly noted otherwise; the exceptions to this rule are energies, which are most frequently reported in kcal/mol, and distances that are normally reported in Å. In the atomic units system, four frequently used quantities (Planck’s constant h divided by 2! [h], mass of electron [me], electron charge [e], and vacuum permittivity [4!e0]) are set explicitly to 1 in the formulas, making these more simple to read. For instance, the Schrödinger equation for the hydrogen atom is in SI units: È 2 e2 ˘ Í - h —2 - ˙ f = E f (1) ÎÍ 2me 4pe0r ˚˙ In atomic units, it looks like: È 1 1˘ - —2 - f = E f (2) ÎÍ 2 r ˚˙ Before a quantity can be used in the atomic units equations, it has to be transformed from SI units into atomic units; the same is true for the quantities obtained from the equations, which can be transformed from atomic units into SI units. For instance, the solution of equation (2) for the ground state of the hydrogen atom gives an energy of –0.5 atomic units (Hartree), which can be converted into other units quite simply by multiplying with the appropriate conversion factor (see table A.1.1).
    [Show full text]
  • Gauss' Theorem (See History for Rea- Son)
    Gauss’ Law Contents 1 Gauss’s law 1 1.1 Qualitative description ......................................... 1 1.2 Equation involving E field ....................................... 1 1.2.1 Integral form ......................................... 1 1.2.2 Differential form ....................................... 2 1.2.3 Equivalence of integral and differential forms ........................ 2 1.3 Equation involving D field ....................................... 2 1.3.1 Free, bound, and total charge ................................. 2 1.3.2 Integral form ......................................... 2 1.3.3 Differential form ....................................... 2 1.4 Equivalence of total and free charge statements ............................ 2 1.5 Equation for linear materials ...................................... 2 1.6 Relation to Coulomb’s law ....................................... 3 1.6.1 Deriving Gauss’s law from Coulomb’s law .......................... 3 1.6.2 Deriving Coulomb’s law from Gauss’s law .......................... 3 1.7 See also ................................................ 3 1.8 Notes ................................................. 3 1.9 References ............................................... 3 1.10 External links ............................................. 3 2 Electric flux 4 2.1 See also ................................................ 4 2.2 References ............................................... 4 2.3 External links ............................................. 4 3 Ampère’s circuital law 5 3.1 Ampère’s original
    [Show full text]
  • Ee334lect37summaryelectroma
    EE334 Electromagnetic Theory I Todd Kaiser Maxwell’s Equations: Maxwell’s equations were developed on experimental evidence and have been found to govern all classical electromagnetic phenomena. They can be written in differential or integral form. r r r Gauss'sLaw ∇ ⋅ D = ρ D ⋅ dS = ρ dv = Q ∫∫ enclosed SV r r r Nomagneticmonopoles ∇ ⋅ B = 0 ∫ B ⋅ dS = 0 S r r ∂B r r ∂ r r Faraday'sLaw ∇× E = − E ⋅ dl = − B ⋅ dS ∫∫S ∂t C ∂t r r r ∂D r r r r ∂ r r Modified Ampere'sLaw ∇× H = J + H ⋅ dl = J ⋅ dS + D ⋅ dS ∫ ∫∫SS ∂t C ∂t where: E = Electric Field Intensity (V/m) D = Electric Flux Density (C/m2) H = Magnetic Field Intensity (A/m) B = Magnetic Flux Density (T) J = Electric Current Density (A/m2) ρ = Electric Charge Density (C/m3) The Continuity Equation for current is consistent with Maxwell’s Equations and the conservation of charge. It can be used to derive Kirchhoff’s Current Law: r ∂ρ ∂ρ r ∇ ⋅ J + = 0 if = 0 ∇ ⋅ J = 0 implies KCL ∂t ∂t Constitutive Relationships: The field intensities and flux densities are related by using the constitutive equations. In general, the permittivity (ε) and the permeability (µ) are tensors (different values in different directions) and are functions of the material. In simple materials they are scalars. r r r r D = ε E ⇒ D = ε rε 0 E r r r r B = µ H ⇒ B = µ r µ0 H where: εr = Relative permittivity ε0 = Vacuum permittivity µr = Relative permeability µ0 = Vacuum permeability Boundary Conditions: At abrupt interfaces between different materials the following conditions hold: r r r r nˆ × (E1 − E2 )= 0 nˆ ⋅(D1 − D2 )= ρ S r r r r r nˆ × ()H1 − H 2 = J S nˆ ⋅ ()B1 − B2 = 0 where: n is the normal vector from region-2 to region-1 Js is the surface current density (A/m) 2 ρs is the surface charge density (C/m ) 1 Electrostatic Fields: When there are no time dependent fields, electric and magnetic fields can exist as independent fields.
    [Show full text]
  • Lesson 9: Coulomb's Law
    Lesson 9: Coulomb's Law Charles Augustin de Coulomb Before getting into all the hardcore physics that surrounds him, it’s a good idea to understand a little about Coulomb. ● He was born in 1736 in Angoulême, France. ● He received the majority of his higher education at the Ecole du Genie at Mezieres (a french military university with a very high reputation, similar to universities like Oxford, Harvard, etc.) from which he graduated in 1761. ● He then spent some time serving as a military engineer in the West Indies and other French outposts, until 1781 when he was permanently stationed in Illustration 1: Paris and was able to devote more time to scientific research. Charles Coulomb Between 1785-91 he published seven memoirs (papers) on physics. ● One of them, published in 1785, discussed the inverse square law of forces between two charged particles. This just means that as you move charges apart, the force between them starts to decrease faster and faster (exponentially). ● In a later memoir he showed that the force is also proportional to the product of the charges, a relationship now called “Coulomb’s Law”. ● For his work, the unit of electrical charge is named after him. This is interesting in that Coulomb was one of the first people to help create the metric system. ● He died in 1806. The Torsion Balance When Coulomb was doing his original experiments he decided to use a torsion balance to measure the forces between charges. ● You already learned about a torsion balance in Physics 20 when you discussed Henry Cavendish’s experiment to measure the value of “G” , the universal gravitational constant.
    [Show full text]
  • Lecture 12 Molecular Dynamics
    Lecture 12 Molecular Dynamics Required reading: Chapter 6: 6.22 –6.23 Karplus, M., and Petsko, G. A. (1990) Molecular dynamics simulations in biology. Nature 347: 631‐639. For further reading on the 2013 Nobel Prize, history and current state of computational methods like MD: Smith and Roux. Structure 21: 2102‐2105. Wednesday: Midterm 1 Reading for Friday: Chapter 7, sections 7.1‐7.19 MCB65 2/22/16 1 Today’s goals • Explain how solvent influences electrostatics • Dielectric constant models polarizability of solvent • Electrostatics influence interactions of ligands • Describe the basic principles behind to molecular dynamics (MD) • Computational simulation of motions of molecules • Challenges and limitations of MD • Examples of insights into protein function from MD MCB65 2/22/16 2 Energy of macromolecules • Component energy terms are assumed to be additive • parameter values – typically pulled from data on small molecules –are assumed to be transferable • Assumptions are likely reasonable for van der Waals and bonded energy terms, but less so for electrostatics Utotal Ubonds U angles U dihedrals U vdw U elec MCB65 Figure from The Molecules of Life (© Garland Science 2008) 2/22/16 3 Solvent effects • Measurements of H‐bonds in gases: • ~10‐20 kJ mol‐1 • ~40 kJ mol‐1 when one partner is charged • Calculations for peptide bond to peptide bond H‐bond in vacuum: • ~20 kJ mol‐1 • Measurement of H‐bond energy in proteins in aqueous buffer: • ~2‐4 kJ mol‐1 • ~4‐8 kJ mol‐1 when one partner is charged • Where does the difference come from? • MCB65 Solvent effect – competition with water 2/22/16 4 Interactions with water weaken H‐bonds • H‐bond energy in solvated proteins: • ~2‐4 kJ mol‐1 (~4‐8 kJ mol‐1 when one partner is charged) • Energy difference between H‐bond with water vs.
    [Show full text]
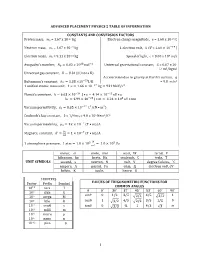
  • Advanced Placement Physics 2 Table of Information
    ADVANCED PLACEMENT PHYSICS 2 TABLE OF INFORMATION CONSTANTS AND CONVERSION FACTORS Proton mass, mp = 1.67 x 10-27 kg Electron charge magnitude, e = 1.60 x 10-19 C !!" Neutron mass, mn = 1.67 x 10-27 kg 1 electron volt, 1 eV = 1.60 × 10 J Electron mass, me = 9.11 x 10-31 kg Speed of light, c = 3.00 x 108 m/s !" !! - Avogadro’s numBer, �! = 6.02 � 10 mol Universal gravitational constant, G = 6.67 x 10 11 m3/kg•s2 Universal gas constant, � = 8.31 J/ mol • K) Acceleration due to gravity at Earth’s surface, g !!" 2 Boltzmann’s constant, �! = 1.38 ×10 J/K = 9.8 m/s 1 unified atomic mass unit, 1 u = 1.66 × 10!!" kg = 931 MeV/�! Planck’s constant, ℎ = 6.63 × 10!!" J • s = 4.14 × 10!!" eV • s ℎ� = 1.99 × 10!!" J • m = 1.24 × 10! eV • nm !!" ! ! Vacuum permittivity, �! = 8.85 × 10 C /(N • m ) CoulomB’s law constant, k = 1/4π�0 = 9.0 x 109 N•m2/C2 !! Vacuum permeability, �! = 4� × 10 (T • m)/A ! Magnetic constant, �‘ = ! = 1 × 10!! (T • m)/A !! ! 1 atmosphere pressure, 1 atm = 1.0 × 10! = 1.0 × 10! Pa !! meter, m mole, mol watt, W farad, F kilogram, kg hertz, Hz coulomB, C tesla, T UNIT SYMBOLS second, s newton, N volt, V degree Celsius, ˚C ampere, A pascal, Pa ohm, Ω electron volt, eV kelvin, K joule, henry, H PREFIXES Factor Prefix SymBol VALUES OF TRIGONOMETRIC FUNCTIONS FOR COMMON ANGLES 10!" tera T � 0˚ 30˚ 37˚ 45˚ 53˚ 60˚ 90˚ 109 giga G sin� 0 1/2 3/5 4/5 1 106 mega M 2/2 3/2 103 kilo k cos� 1 3/2 4/5 2/2 3/5 1/2 0 10-2 centi c tan� 0 3/3 ¾ 1 4/3 3 ∞ 10-3 milli m 10-6 micro � 10-9 nano n 10-12 pico p 1 ADVANCED PLACEMENT PHYSICS 2 EQUATIONS MECHANICS Equation Usage �! = �!! + �!� Kinematic relationships for an oBject accelerating uniformly in one 1 dimension.
    [Show full text]
  • Introduction Particle Physics 2
    Introduction 1 Particle Physics 2 • [0] L.Wainstein and V.Zubakov, Extraction of signals from noise, ISBN 0-486-62625-3 • The course PHZ 7357 is taught from the phenomenological and experimental perspectives, covering in depth the underlying theoretical and experimental concepts in particle physics. Prof. S. Klimenko PHZ 7357, Fall 2017 Time line of particle discoveries 2 X-rays nt H Prof. S. Klimenko PHZ 7357, Fall 2017 Standard Model building blocks 3 matter force strong electromag. weak weak Prof. S. Klimenko PHZ 7357, Fall 2017 Where are we today? 4 • All particles are made up of spin ½ fermions (leptons & quarks – are there other building blocks?) • Quarks and leptons appear to be fundamental (point-like) – no evidence for their constituents • Fundamental “matter” is organized in 3 generations (why 3?) • Carriers of force are integer spin bosons Ø quark interactions are strong (g), weak (W,Z), EM (g) and gravity Ø lepton interactions are weak (W,Z), EM (g) and gravity Ø strong & EM forces are long-range – mg=mg=0 Ø weak force is short-range – mw~mz ~ 90 GeV Ø the 4th force of nature – gravity – is not part of SM • All other particles are hadrons Ø mesons - ��" quarks bounded state, like K,p,.. Ø baryons – 3 quarks bounded state, like proton, neutron, .. Ø no free quarks have been observed. • Neutrinos have small mass - why so small? • …. Prof. S. Klimenko PHZ 7357, Fall 2017 Standard Model Interactions 5 • Fundamental interaction force is given by charge g related to dimensionless coupling constant ag. , • for the EM force: in Natural Units �%& = � = 4�� • Properties of the gauge bosons and nature of the interaction between the bosons and fermions determine the properties of the interaction 240 Prof.
    [Show full text]
  • KJM 3110 Electrochemistry Chapter 1. Electricity
    KJM 3110 Electrochemistry Chapter 1. Electricity Electricity • In this chapter we will familiarise ourselves with the most fundamental concepts of electricity itself. • Charge Different disciplines, textbooks, articles, teachers use different symbols for many of these entities. For instance, e vs q, q vs Q, f vs • Electrostatic force F, U vs E, i vs I… • Electrical work We could try to be completely consistent here. • Potential and voltage • Capacitance Instead we allow variations, to train ourselves for reality, but aim to always define and/or • Current make clear what we mean. • Conductance and resistance • DC and AC voltage and current and impedance Electrical charge • Charge is a physical property of matter that causes repulsive or attractive forces between objects of charge of the same or opposite sign. • Charge is quantized in multiples of e • The unit of electrical charge is C, coulomb • e = 1.602×10−19 C • As symbol of charge we use, for instance, q. • A proton has charge e Charles-Augustin de Coulomb • An electron has charge –e (1736-1806) • Neutrons have charge 0 • (Quarks have charges that are multiples of e/3) ke q1q2 q1q2 • Force between charges F F 2 2 r 4 r -12 2 2 0 • Dielectric permittivity of vacuum ε0 = 8.854x10 C /Nm Electroneutrality • Charges of equal sign repel each other • Tend to get max distance • Net charge seeks to external boundaries (surfaces, interfaces) • Interior (bulk) phases remain electroneutral • Electroneutrality: Sum of negative and positive charges balance (cancel) each other Electrical field;
    [Show full text]
  • Magnetic Field
    Magnetic and electric properties of quantum vacuum Rémy Battesti, Carlo Rizzo To cite this version: Rémy Battesti, Carlo Rizzo. Magnetic and electric properties of quantum vacuum. Reports on Progress in Physics, IOP Publishing, 2013, in press. hal-00748539 HAL Id: hal-00748539 https://hal.archives-ouvertes.fr/hal-00748539 Submitted on 5 Nov 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Magnetic and electric properties of quantum vacuum R. Battesti, C. Rizzo Laboratoire National des Champs Magn´etiques Intenses, 143 avenue de Rangueil, 31400 Toulouse, France. E-mail: [email protected] Abstract. In this report we show that vacuum is a nonlinear optical medium and we discuss what are the optical phenomena that should exist in the framework of the standard model of particle physics. We pay special attention to the low energy limit. The predicted effects for photons of energy smaller than the electron rest mass are of such a level that none has been observed experimentally yet. Progresses in field sources and related techniques seem to indicate that in few years vacuum nonlinear optics will be accessible to human investigation.
    [Show full text]
  • Macroscopic Maxwell Equations
    J. Förstner How HPC helps exploring electromagnetic near fields Jens Förstner Theoretical Electrical Engineering Outline J. Förstner • Maxwell equations • some analytical solutions – homogeneous media – point-like sources • challenges for wavelength-sized structures • examples from the TET group Maxwell equations J. Förstner Starting point of this talk are the macroscopic Maxwell equations: div 퐷(푟Ԧ, 푡) = 휌(푟Ԧ, 푡) Gauss's law (Electric charges are the source of electro-static fields) Gauss's law for magnetism div 퐵(푟Ԧ, 푡) = 0 (There are no free magnetic charges/monopoles) curl 퐸(푟Ԧ, 푡) = −휕푡퐵(푟Ԧ, 푡) Faraday's law of induction (changes in the magnetic flux electric ring fields) curl 퐻(푟Ԧ, 푡) = 휕 퐷(푟Ԧ, 푡) + 퐽Ԧ (푟Ԧ, 푡) Ampere's law with Maxwell's addition 푡 (currents and changes in the electric flux density magnetic ring fields) 퐸 electric field strength 퐻 magnetic field strength 퐷 electric flux density 퐵 magnetic flux density 푑 휕푡 ≔ 푃Ԧ macroscopic polarization 푃Ԧ magnetic dipole density 푑푡 휌 free electric charge density 퐽Ԧ free electric current density 퐶2 푁 휀 = 8.85 ⋅ 10−12 vacuum permittivity 휇 = 4휋10−7 vacuum permeability 0 푁푚2 0 퐴2 Maxwell theory J. Förstner - magnetism (earth, compass) DC - binding force between electrons & nucleus => atoms pg - binding between atoms => molecules and solids l.j AC circuit - <1 kHz: electricity, LF electronics - antennas, radation: radio, satellites, cell phones, radar - metallic waveguides: TV, land-line communication, power transmission, HF electronics - lasers, LEDs, optical fibers Full range of effects are described by the - medical applications same theory: Maxwell equations However the material response depends - X-Ray scanning strongly on the frequency.
    [Show full text]
  • Chapter 4. Electrostatics of Macroscopic Media
    Chapter 4. Electrostatics of Macroscopic Media 4.1 Multipole Expansion Approximate potentials at large distances x 3 x x' d x' x' (x') x a Fig 4.1 We consider the potential in the far-field region (see Fig. 4.1 where | | ) due to a localized charge distribution ( for ). If the total charge is q, it is a good approximation to treat the charge distribution as a point charge, so . Even if q is zero, the potential does not vanish, but it decays much faster than . We will discuss more details about how the potential behaves in the far-field region. Electric dipole r+ +q x r- Fig 4.2. An electric dipole consists of two d equal and opposite charges +q and –q separated by a displacement d. -q We begin with a simple, yet exceedingly important case of charge distribution. Two equal and opposite charges separated by a small distance form an electric dipole. Suppose that +q and –q are separated by a displacement vector d as shown in Figure 4.2, then the potential at x is ( ) [( ) ( ) ] (4.1) 1 In the far-field region for | | , (4.2) [( ) ( )] This reduces to the coordinate independent expression (4.3) where is the electric dipole moment. For the dipole p along the z-axis, the electric fields take the form (4.4) { From this, we can obtain the coordinate independent expression (4.5) where is a unit vector. Fig 4.3. Field of an electric dipole 2 Multipole expansion We can expand the potential due to the charge distribution (1.12) ∫ | | using Eq.
    [Show full text]