Multiscale-Failure Criteria of Carbon Nanotube Systems Under Biaxial Tension–Torsion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Executive Summary ¾ Electricity Report ¾ Natural Gas Report ¾ Communications Report ¾ Water/Wastewater Report ¾ Acronyms ¾ Glossary
Indiana Utility Regulatory Commission 2007 Regulatory Flexibility Report to the Indiana General Assembly Links to Major Sections of the Regulatory Flexibility Report Click on Links Below to Navigate to Major Sections of the Regulatory Flexibility Report ¾ Executive Summary ¾ Electricity Report ¾ Natural Gas Report ¾ Communications Report ¾ Water/Wastewater Report ¾ Acronyms ¾ Glossary Executive Summary EXECUTIVE SUMMARY This 2007 Indiana Utility Regulatory Commission Report to the Regulatory Flexibility Committee of the Indiana General Assembly highlights key issues that confront Indiana Electric, Gas, Communications, and Water/Wastewater industries, as well as the role of the Indiana Utility Regulatory Commission (IURC, Commission) in addressing these issues. For the first time, and while not required by statute, a section on the Water/Wastewater industry is included in this Report in response to concerns raised during the most recent session of the legislature. While each industry has unique issues, several issues discussed in this Report cut across multiple industries. This Executive Summary contains a brief overview of these cross-industry and industry-specific issues which are more fully addressed in the body of the Report. For your convenience there is a list of acronyms and a glossary in the back of the Report. CROSS-INDUSTRY ISSUES Aging infrastructure is a concern for many Indiana utilities. The Electric, Gas, and Water/Wastewater sections of this Report specifically discuss aging infrastructure and the potential problems and costs associated with repairing or replacing old facilities. Coupled with aging facilities is increasing consumer demand for electric, gas, telecommunications, and water services. Increased consumer demand can accelerate the deterioration of equipment and limit periods in which facilities can be conveniently removed from service for maintenance or replacement. -

TX-NR636 AV RECEIVER Advanced Manual
TX-NR636 AV RECEIVER Advanced Manual CONTENTS AM/FM Radio Receiving Function 2 Using Remote Controller for Playing Music Files 15 TV operation 42 Tuning into a Radio Station 2 About the Remote Controller 15 Blu-ray Disc player/DVD player/DVD recorder Presetting an AM/FM Radio Station 2 Remote Controller Buttons 15 operation 42 Using RDS (European, Australian and Asian models) 3 Icons Displayed during Playback 15 VCR/PVR operation 43 Playing Content from a USB Storage Device 4 Using the Listening Modes 16 Satellite receiver / Cable receiver operation 43 CD player operation 44 Listening to Internet Radio 5 Selecting Listening Mode 16 Cassette tape deck operation 44 About Internet Radio 5 Contents of Listening Modes 17 To operate CEC-compatible components 44 TuneIn 5 Checking the Input Format 19 Pandora®–Getting Started (U.S., Australia and Advanced Settings 20 Advanced Speaker Connection 45 New Zealand only) 6 How to Set 20 Bi-Amping 45 SiriusXM Internet Radio (North American only) 7 1.Input/Output Assign 21 Connecting and Operating Onkyo RI Components 46 Slacker Personal Radio (North American only) 8 2.Speaker Setup 24 About RI Function 46 Registering Other Internet Radios 9 3.Audio Adjust 28 RI Connection and Setting 46 DLNA Music Streaming 11 4.Source Setup 29 iPod/iPhone Operation 47 About DLNA 11 5.Listening Mode Preset 32 Firmware Update 48 Configuring the Windows Media® Player 11 6.Miscellaneous 32 About Firmware Update 48 DLNA Playback 11 7.Hardware Setup 33 Updating the Firmware via Network 48 Controlling Remote Playback from a PC 12 8.Remote Controller Setup 39 Updating the Firmware via USB 49 9.Lock Setup 39 Music Streaming from a Shared Folder 13 Troubleshooting 51 Operating Other Components Using Remote About Shared Folder 13 Reference Information 57 Setting PC 13 Controller 40 Playing from a Shared Folder 13 Functions of REMOTE MODE Buttons 40 Programming Remote Control Codes 40 En AM/FM Radio Receiving Function Tuning into stations manually 2. -
ONN 6 Eng Codelist Only Webversion.Indd
6-DEVICE UNIVERSAL REMOTE Model: 100020904 CODELIST Need help? We’re here for you every day 7 a.m. – 9 p.m. CST. Give us a call at 1-888-516-2630 Please visit the website “www.onn-support.com” to get more information. 1 TABLE OF CONTENTS CODELIST TV 3 STREAM 5 STB 5 AUDIO SOUNDBAR 21 BLURAY DVD 22 2 CODELIST TV TV EQD 2014, 2087, 2277 EQD Auria 2014, 2087, 2277 Acer 4143 ESA 1595, 1963 Admiral 3879 eTec 2397 Affinity 3717, 3870, 3577, Exorvision 3953 3716 Favi 3382 Aiwa 1362 Fisher 1362 Akai 1675 Fluid 2964 Akura 1687 Fujimaro 1687 AOC 3720, 2691, 1365, Funai 1595, 1864, 1394, 2014, 2087 1963 Apex Digital 2397, 4347, 4350 Furrion 3332, 4093 Ario 2397 Gateway 1755, 1756 Asus 3340 GE 1447 Asustek 3340 General Electric 1447 Atvio 3638, 3636, 3879 GFM 1886, 1963, 1864 Atyme 2746 GPX 3980, 3977 Audiosonic 1675 Haier 2309, 1749, 1748, Audiovox 1564, 1276, 1769, 3382, 1753, 3429, 2121 2293, 4398, 2214 Auria 4748, 2087, 2014, Hannspree 1348, 2786 2277 Hisense 3519, 4740, 4618, Avera 2397, 2049 2183, 5185, 1660, Avol 2735, 4367, 3382, 3382, 4398 3118, 1709 Hitachi 1643, 4398, 5102, Axen 1709 4455, 3382, 0679 Axess 3593 Hiteker 3118 BenQ 1756 HKPro 3879, 2434 Blu:sens 2735 Hyundai 4618 Bolva 2397 iLo 1463, 1394 Broksonic 1892 Insignia 2049, 1780, 4487, Calypso 4748 3227, 1564, 1641, Champion 1362 2184, 1892, 1423, Changhong 4629 1660, 1963, 1463 Coby 3627 iSymphony 3382, 3429, 3118, Commercial Solutions 1447 3094 Conia 1687 JVC 1774, 1601, 3393, Contex 4053, 4280 2321, 2271, 4107, Craig 3423 4398, 5182, 4105, Crosley 3115 4053, 1670, 1892, Curtis -

PUBLIC NOTICE Federal Communications Commission Th News Media Information 202 / 418-0500 445 12 St., S.W
PUBLIC NOTICE Federal Communications Commission th News Media Information 202 / 418-0500 445 12 St., S.W. Internet: http://www.fcc.gov Washington, D.C. 20554 TTY: 1-888-835-5322 DA 07-3252 Released: July 27, 2007 Media Bureau Notice Deadline for Filing Mandatory EEO Form 396-C Is October 1, 2007 FCC Form 396-C, Multi-Channel Video Programming Distributor EEO Program Annual Report (September 2003 Edition) is due to be filed electronically with the Commission by midnight on October 1, 2007. This is because the normal deadline of September 30 falls on a Sunday this year. Users can access the electronic filing system via the Internet from the Commission’s Web Site at: http://svartifoss2.fcc.gov/cgi-bin/ws.exe/prod/cdbs/forms/prod/cdbsmenu.hts Paper versions of the form will not be accepted unless accompanied by an appropriate request for waiver of the electronic filing requirement. The Commission has recognized the need for limited waivers of the electronic filing requirement in light of the “burden that electronic filing could place upon some [entities] who are seeking to serve the public interest, with limited resources, and succeed in a highly competitive local environment.” Streamlining Order, 13 FCC Rcd 23061. However, such waivers will not be routinely granted and the applicant must plead with particularity the facts and circumstances warranting relief. Similar to prior years, selected Multi-Channel Video Programming Distributors (“MVPDs”) will be required to fill out portions of the Supplemental Investigation Sheet (“SIS”) at the end of the form. MVPDs, when they attempt to file Form 396-C electronically, will see a box on page one of the electronic version of the form next to the statement “Supplemental Investigation Sheet attached.” If the box is not checked, this means the filer does not need to file the SIS this year. -

Counselors Who Seal the Deals in Cable
specialreport DEAL-MAKERS: ATTORNEYS AT LARGE Counselors Who Seal the Deals in Cable IN A TRANSitiONAL YEAR, HERE ARE NINE AttORNEYS TO KNOW BY GARY ARLEN from the pending Comcast-Time Warner Cable and AT&T-DirecTV mergers, as well as the impact of the FCC’s Open Internet order. They have a unique perspective on what happens ohn Quincy Adams once said of the legal system, “Whoever tells the best story after a big merger, such as vendor consolidation. These “outside counsel” examine the im- wins.” The same holds try for the lawyers who close cable’s biggest deals. pact of today’s all-time high equity valuations and what the tightening credit markets will J Nine leading cable-industry attorneys offer their visions of what the business — and mean for cable transactions. Their views vary on the significance of issues such as retrans- they — will face in the coming year. Among the storylines they’re following: ripple effects mission consent and intellectual property, and help shape the narrative of the TV industry. Lee D. Charles Ariel Deckelbaum Partner, Baker Botts LLP, New York Partner and Deputy Chair, Corporate Department, Paul, Weiss, Rifkind, Wharton & Garrison LLP, New York Background: In his 25 years representing MSOs, pro- gram networks and companies that provide services Background: In addition to his cable projects — largely to both categories, Charles has been involved in many for Time Warner Cable — Deckelbaum has represented firsts. He worked on Discovery Communications’s Goldman Sachs in the sale of a 50% interest in TV show first acquisition (The Learning Channel, now TLC) CSI: Crime Scene Investigation and its related intellectual and on the creation of the YES Network on behalf property; he handled the acquisition of ViaWest by Oak of the New York Yankees. -

Telecommunications Service Providers IAC Codes, Exchange Carrier Names, Company Codes - Telcordia and Regions
COMMON LANGUAGE® Telecommunications Service Providers IAC Codes, Exchange Carrier Names, Company Codes - Telcordia and Regions Telcordia Technologies Practice BR-751-100-112 Issue 2 April 1999 Proprietary — Licensed Material Possession or use of this material or any of the COMMON LANGUAGE Codes, Rules, and Information disclosed herein requires a written license agreement and is governed by its terms and conditions. For more information, visit www.commonlanguage.com/notices. An SAIC Company BR-751-100-112 TSP IAC Codes, EC names, Company Codes - Telcordia and Regions Issue 2 Copyright Page April 1999 COMMON LANGUAGE® Telecommunications Service Providers IAC Codes, Exchange Carrier Names, Company Codes - Telcordia and Regions Prepared for Telcordia Technologies by: Lois Modrell Target audience: Telecommunications Service Providers This document replaces: BR-751-100-112, Issue 1, March 1998 Technical contact: Lois Modrell To obtain copies of this document, contact your company’s document coordinator or call 1-800-521-2673 (from the USA and Canada) or 1-732-699-5800 (all others), or visit our Web site at www.telcordia.com. Telcordia employees should call (732) 699-5802. Copyright © 1997-1999 Telcordia Technologies, Inc. All rights reserved. Project Funding Year: 1999 Trademark Acknowledgments Telcordia is a trademark of Telcordia Technologies, Inc. COMMON LANGUAGE is a registered trademark of Telcordia Technologies. Proprietary — Licensed Material See confidentiality restrictions on title page. 2 BR-751-100-112 Issue 2 TSP IAC Codes, EC Names, Company Codes - Telcordia and Regions April 1999 Disclaimer Notice of Disclaimer This document is issued by Telcordia Technologies, Inc. to inform Telcordia customers of the Telcordia practice relating to COMMON LANGUAGE® Telecommunications Service Providers IAC Codes, Exchange Carrier Names - Company Codes - Telcordia and Regions. -

NSTAC Report to the President on Emergency Communications and Interoperability
THE PRESIDENT’S NATIONAL SECURITY TELECOMMUNICATIONS ADVISORY COMMITTEE NSTAC Report to the President on Emergency Communications and Interoperability January 16, 2007 President’s National Security Telecommunications Advisory Committee TABLE OF CONTENTS EXECUTIVE SUMMARY ................................................................................................................. ES–1 1.0 INTRODUCTION .........................................................................................................................1 1.1 Background and Charge.......................................................................................... 1 1.2 Approach................................................................................................................. 3 1.3 Scope of the NSTAC Review ................................................................................. 3 1.4 Report Organization................................................................................................ 5 2.0 EXPANSION OF NATIONAL SECURITY AND EMERGENCY PREPAREDNESS PRIORITY SERVICES AND DEPLOYABLE CAPABILITIES.............................................7 2.1 Deployable Communications Capabilities.............................................................. 8 2.2 Telecommunications Service Priority Enhancement for Wireless .......................... Networks............................................................................................................... 13 3.0 INPUTS TO THE NATIONAL EMERGENCY COMMUNICATIONS STRATEGY........17 -

Missouri Public Service Commission Director, Utility Services CONNIE MURRAY NATELLE DIETRICH POST OFFICE BOX 360 Director, Utility Operations ROBERT M
WESS A . HENDERSON ' Executive Director DANA K . JOYCE Director, Administration and Commissioners Regulatory Policy JEFF DAVIS ROBERT SCHALLENBERG Chairman Missouri Public Service Commission Director, Utility Services CONNIE MURRAY NATELLE DIETRICH POST OFFICE BOX 360 Director, Utility Operations ROBERT M . CLAYTON III JEFFERSON CITY MISSOURI 65102 COLLEEN M. DALE 573-751-3234 TERRY JARRETT Secretary/Chief Regulatory Law Judge 573-751-1847 (Fax Number) KEVIN GUNN http ://www.psc.mo.gov KEVIN A. THOMPSON General Counsel August 28, 2008 Mr. Greg Steinho ff . Director Missouri Department of Economic Development Room 680, Truman Building Jefferson City, MO 65102 Dear Mr. Steinhoff: On behalf of the Missouri Public Service Commission, I am pleased to forward our report on developments resulting from the implementation of the 2007 Video Services Providers Act . As provided in Section 67.2693 RSMo the Commission is required to submit this report on August 28, 2008 and for the next three years thereafter. This report offers some limited findings ; however there are several areas where critical information or Commission authority is lacking to allow a full and accurate assessment of the effects of the Act . I hope you find this information useful, and don't hesitate to contact me at 751-3233 or Wess Henderson, PSC Executive Director, at 751-3684 if you have questions. Enclosure cc Governor Blunt, Hon. Rod Jetton Hon. Michael Gibbons Members of the Senate Committee on Commerce and Environment Members of the House Special Committee on Utilities -
Control Remoto Universal Para 4 Dispositivos NS-RMT415
GUÍA DEL USUARIO Control remoto universal para 4 dispositivos NS-RMT415 APPS Antes de usar su producto nuevo, lea este instructivo para evitar cualquier daño. 1 CONTENIDO DEL PAQUETE • Control remoto universal para 4 dispositivos • Guía del usuario CARACTERÍSTICAS • Funciona con un televisor, reproductor de DVD o Blu-Ray, decodifi cador de cable y dispositivo de transmisión en continuo • Programación por nombres de marcas populares para una instalación rápida y fácil • Biblioteca de códigos amplia para las marcas y dispositivos menos comunes • Diseño exclusivo, materiales y fabricación para un uso exigente INSTALACIÓN DE LAS PILAS • Inserte dos pilas AA (no incluidas) en el control remoto. Verifi que que los símbolos + y – en las pilas correspondan con los símbolos + y – en el compartimiento de las pilas. Nota: Para confi gurar su control remoto, siga los pasos de instalación a continuación en orden y DETÉNGASE tan pronto como su control remoto funciona correctamente. PROGRAMACIÓN DE SU CONTROL REMOTO Hay tres formas para confi gurar su control remoto: • Use el “Método de confi guración A: Marcas conocidas” para marcas conocidas preprogramadas. • Use el “Método de confi guración B: de entrada de código directo” si el código directo de su dispositivo está situado en la página posterior. • Use el “Método de confi guración C: búsqueda de código” para efectuar una búsqueda de código para su dispositivo. Nota: Este control remoto está preestablecido para televisores Insignia y reproductores de DVD, cajas decodifi cadoras DIRECTV y transmisión en continuo AppleTV. Si el control remoto no funciona con su dispositivo, use el método B o C para cambiar la confi guración. -
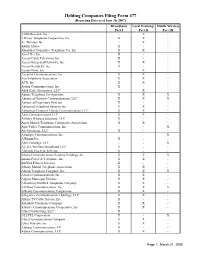
Holding Companies Filing Form 477 (Reporting Data As of June 30, 2007) Broadband Local Exchange Mobile Wireless Part I Part II Part III 1-800-Reconex, Inc
Holding Companies Filing Form 477 (Reporting Data as of June 30, 2007) Broadband Local Exchange Mobile Wireless Part I Part II Part III 1-800-Reconex, Inc. - X - 3 Rivers Telephone Cooperative, Inc. X X - A+ Wireless Inc. - X - Ability House X - - Absaraka Cooperative Telephone Co., Inc. X X - Accel Net, Inc. X - - Access Cable Television, Inc. X - - Access Integrated Networks, Inc. X X - Access Kentucky, Inc. X - - Access Point, Inc. - X - Accipiter Communications, Inc. X X - Ace Telephone Association X X - ACN, Inc. X X - Action Communications, Inc. X - - Adak Eagle Enterprises, LLC - X - Adams Telephone Co-Operative X X X Advanced Network Communications, LLC X X X Advanced Proprietary Systems X - - Advanced Telephone Systems Inc. X X - Advantage Group of Florida Communications LLC X X - Aero Communications LLC X X - Affinity Wireless Solutions, LLC X - - Agate Mutual Telephone Cooperative Association X X - Agri-Valley Communications, Inc. - - X Air Advantage, LLC X - - Airadigm Communications, Inc. - - X AIRbaud Inc. X - - AKD Holdings, LLC - - X AL-GA Wireless Broadband, LLC X - - Alameda Power & Telecom X - - Alaska Communications Systems Holdings, Inc. X X X Alaska Power & Telephone, Inc. X X - AlaWeb Pioneer Services X - - Albany Mutual Telephone Association X X - Albion Telephone Company, Inc. X X X Alenco Communications, Inc. X X - Algona Municipal Utilities X X - Alhambra-Grantfork Telephone Company X X - All West Communications, Inc. X X X Allband Communications Cooperative X X - Allegiance Communications Holdings, LLC X X - Allen's TV Cable Service, Inc. X - - Allendale Telephone Company X X - Alliance Communications Cooperative, Inc. X X - Allnet Networking, LLC X - - ALLTEL Corporation X - X Alma Communications Company X X - Alma Telecom, Inc. -

December 10, 2008 Ms. Marlene H. Dortch Secretary Federal
December 10, 2008 Jenner & Block LLP Chicago 1099 New York Avenue, NW New York Suite 900 Washington, DC Washington, DC 20001 Tel 202-639-6000 www.jenner.com Ms. Marlene H. Dortch Mark D. Schneider Tel 202 639-6005 Secretary Fax 202 661-4945 Federal Communications Commission [email protected] 445 Twelfth Street, S.W. Washington, D.C. 20554 Re: Application to Transfer of Control of Domestic Authorizations Held by Embarq Corporation to CenturyTel, Inc. Under Section 214 of the Communications Act, WC Docket No. 08-238 Dear Ms. Dortch: In response to the Wireline Competition Bureau’s request, the attached exhibits list the providers that Embarq and CenturyTel have identified through several databases in the markets where they operate in adjacent exchanges. Because each company uses different sources to identify providers, we have separated the lists into two exhibits, one for Embarq and one for CenturyTel. Embarq’s provider list is compiled from five sources: (1) the MediaPrints database; (2) Ported Line Reports dating back to August 2006; (3) UNE LOOP & UNEP Reports; (4) internal wholesale reseller accounts; and (5) cell tower sites. CenturyTel’s provider list is compiled from four sources: (1) wholesale billing accounts; (2) internal marketing data; (3) Port Away reports dating back to December 2006; and (4) data from USAC. In addition, we have attached an exhibit containing maps of all adjacent exchanges. For your convenience, the two competitor list exhibits reference the map number where each adjacent exchange is located. Please let -

Social Media and Emergency Management
Chapter 11: Social Media and Emergency Management CHAPTER 11: SOCIAL MEDIA AND EMERGENCY MANAGEMENT Academic Contributors: Dr. Amanda L. Hughes and Dr. Leysia Palen Practitioner Contributor: Steve Peterson ABSTRACT This chapter reports on the challenges and opportunities made possible by social media in the field of emergency management. First, we consider the emergency practitioner and the challenges they face when using social media: difficulties in verifying social media data, liability risks, information overload, and a lack of resources to manage social media communications and data. To address these challenges, we propose the use of performance measures, standards, best practices, digital volunteers, training, and exercises. Attention then turns to the research around social media in times of crisis. This research investigates public activity (citizen reporting, community-oriented computing, and collective intelligence and distributed problem solving) and demonstrates how social media have shaped—and continue to shape—perceptions around how members of the public can participate in an emergency. We then look at research that studies emergency management organizations as they seek to understand how social media might be used in their practice. We conclude with descriptions of future research directions and next-generation tools for monitoring and extracting information from social media. Finally, we discuss the differences between practice and research perspectives and discuss how these differences can make it difficult to reach consensus regarding social media’s role in emergency response. We advocate that as practice and research work together expanding the research agenda, understanding roles, building relationships, considering organizational fit, and developing best practices, they will advance knowledge about the potential and realities of social media and move toward envisioning how social media may be used as a resource in emergency management.