Measuring Noise Correlation for Improved Video Denoising
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ACM Multimedia 2007
ACM Multimedia 2007 Call for Papers (PDF) University of Augsburg Augsburg, Germany September 24 – 29, 2007 http://www.acmmm07.org ACM Multimedia 2007 invites you to participate in the premier annual multimedia conference, covering all aspects of multimedia computing: from underlying technologies to applications, theory to practice, and servers to networks to devices. A final version of the conference program is now available. Registration will be open from 7:30am to 7pm on Monday and 7:30am to 5pm on Tuesday, Wednesday and Thursday On Friday registration is only possible from 7:30am to 1pm. ACM Business Meeting is schedule for Wednesday 9/26/2007 during Lunch (Mensa). Ramesh Jain and Klara Nahrstedt will talk about the SIGMM status SIGMM web status Status of other conferences/journals (TOMCCAP/MMSJ/…) sponsored by SIGMM Miscellaneous Also Chairs of MM’08 will give their advertisement Call for proposals for MM’09 + contenders will present their pitch Announcement of Euro ACM SIGMM Miscellaneous Travel information: How to get to Augsburg How to get to the conference sites (Augsburg public transport) Conference site maps and directions (excerpt from the conference program) Images of Augsburg The technical program will consist of plenary sessions and talks with topics of interest in: (a) Multimedia content analysis, processing, and retrieval; (b) Multimedia networking, sensor networks, and systems support; (c) Multimedia tools, end-systems, and applications; and (d) Multimedia interfaces; Awards will be given to the best paper and the best student paper as well as to best demo, best art program paper, and the best-contributed open-source software. -

All You Need to Know About SINAD Measurements Using the 2023
applicationapplication notenote All you need to know about SINAD and its measurement using 2023 signal generators The 2023A, 2023B and 2025 can be supplied with an optional SINAD measuring capability. This article explains what SINAD measurements are, when they are used and how the SINAD option on 2023A, 2023B and 2025 performs this important task. www.ifrsys.com SINAD and its measurements using the 2023 What is SINAD? C-MESSAGE filter used in North America SINAD is a parameter which provides a quantitative Psophometric filter specified in ITU-T Recommendation measurement of the quality of an audio signal from a O.41, more commonly known from its original description as a communication device. For the purpose of this article the CCITT filter (also often referred to as a P53 filter) device is a radio receiver. The definition of SINAD is very simple A third type of filter is also sometimes used which is - its the ratio of the total signal power level (wanted Signal + unweighted (i.e. flat) over a broader bandwidth. Noise + Distortion or SND) to unwanted signal power (Noise + The telephony filter responses are tabulated in Figure 2. The Distortion or ND). It follows that the higher the figure the better differences in frequency response result in different SINAD the quality of the audio signal. The ratio is expressed as a values for the same signal. The C-MES signal uses a reference logarithmic value (in dB) from the formulae 10Log (SND/ND). frequency of 1 kHz while the CCITT filter uses a reference of Remember that this a power ratio, not a voltage ratio, so a 800 Hz, which results in the filter having "gain" at 1 kHz. -

AN10062 Phase Noise Measurement Guide for Oscillators
Phase Noise Measurement Guide for Oscillators Contents 1 Introduction ............................................................................................................................................. 1 2 What is phase noise ................................................................................................................................. 2 3 Methods of phase noise measurement ................................................................................................... 3 4 Connecting the signal to a phase noise analyzer ..................................................................................... 4 4.1 Signal level and thermal noise ......................................................................................................... 4 4.2 Active amplifiers and probes ........................................................................................................... 4 4.3 Oscillator output signal types .......................................................................................................... 5 4.3.1 Single ended LVCMOS ........................................................................................................... 5 4.3.2 Single ended Clipped Sine ..................................................................................................... 5 4.3.3 Differential outputs ............................................................................................................... 6 5 Setting up a phase noise analyzer ........................................................................................................... -

Topic 5: Noise in Images
NOISE IN IMAGES Session: 2007-2008 -1 Topic 5: Noise in Images 5.1 Introduction One of the most important consideration in digital processing of images is noise, in fact it is usually the factor that determines the success or failure of any of the enhancement or recon- struction scheme, most of which fail in the present of significant noise. In all processing systems we must consider how much of the detected signal can be regarded as true and how much is associated with random background events resulting from either the detection or transmission process. These random events are classified under the general topic of noise. This noise can result from a vast variety of sources, including the discrete nature of radiation, variation in detector sensitivity, photo-graphic grain effects, data transmission errors, properties of imaging systems such as air turbulence or water droplets and image quantsiation errors. In each case the properties of the noise are different, as are the image processing opera- tions that can be applied to reduce their effects. 5.2 Fixed Pattern Noise As image sensor consists of many detectors, the most obvious example being a CCD array which is a two-dimensional array of detectors, one per pixel of the detected image. If indi- vidual detector do not have identical response, then this fixed pattern detector response will be combined with the detected image. If this fixed pattern is purely additive, then the detected image is just, f (i; j) = s(i; j) + b(i; j) where s(i; j) is the true image and b(i; j) the fixed pattern noise. -

Youtube Buys Green Parrot Pictures 15 March 2011
YouTube buys Green Parrot Pictures 15 March 2011 quality, steadier video -- all while your video is simply being uploaded to the site?" Technology developed by Green Parrot Pictures "can do exactly this," Doig said, and has been used by major studios on films such as "Lord of the Rings," "X-Men" and "Spider-Man." "Their technology helps make videos look better while at the same time using less bandwidth and improving playback speed," Doig said. Google-owned YouTube said Tuesday that it has bought (c) 2011 AFP an Irish digital video company whose technology can help improve the quality of amateur footage submitted to the video-sharing site. Google-owned YouTube said Tuesday that it has bought an Irish digital video company whose technology can help improve the quality of amateur footage submitted to the video-sharing site. Financial details of the acquisition of Green Parrot Pictures, which was founded by Anil Kokaram, an associate professor at the engineering school of Trinity College in Dublin, were not disclosed. YouTube said in a blog post that much of the 35 hours of video uploaded to the site every minute is "beautifully shot by professionals or aspiring filmmakers." "But some of YouTube's most popular or moving videos are shot using low-quality mobile phones and video cameras," said Jeremy Doig, director of Google Video Technology. "Take, for example, videos of recent protests in Libya," Doig said. "Although emotionally captivating, they can be jerky, blurry or unsteady. "What if there was a technology that could improve the quality of such videos -- sharpening the image, reducing visual noise and rendering a higher- 1 / 2 APA citation: YouTube buys Green Parrot Pictures (2011, March 15) retrieved 24 September 2021 from https://phys.org/news/2011-03-youtube-green-parrot-pictures.html This document is subject to copyright. -

ICIP 2007 Session Index
ICIP 2007 Session Index Monday Morning MA-L1: Video Coding for Next Generation Displays MA-L2: Image And Video Segmentation I MA-L3: Video Coding I MA-L4: Image and Video Restoration MA-L5: Biometrics I MA-L6: Image and Video Storage and Retrieval I MA-P1: Stereoscopic and 3D Processing I: Coding and Processing MA-P2: Active-Contour, Level-Set, and Cluster-Based Segmentation Methods MA-P3: Image and Video Denoising MA-P4: Biometrics II: Human Activity, Gait, Gaze Analysis MA-P5: Security I: Authentication and Steganography MA-P6: Image and Video Multiresolution Processing MA-P7: Motion Detection and Estimation I MA-P8: Image and Video Enhancement Monday Afternoon MP-L1: Distributed Source Coding I: Low Complexity Video Coding MP-L2: Image And Video Segmentation II: Texture Segmentation MP-L3: Interpolation and Superresolution I MP-L4: Image and Video Modeling I MP-L5: Security II MP-L6: Image Scanning, Display, Printing, Color and Multispectral Processing I MP-P1: Image and Video Storage and Retrieval II MP-P2: Morphological, Level-Set, and Edge or Color Image/Video Segmentation MP-P3: Scalable Video Coding MP-P4: Image Coding I MP-P5: Biometrics III: Fingerprints, Iris, Palmprints MP-P6: Biomedical Imaging I MP-P7: Motion Detection and Estimation II MP-P8: Stereoscopic and 3D Processing II: 3D Modeling & Synthesis Tuesday Morning TA-L1: Distributed Source Coding II: Distributed Image and Video Coding and Their Applications TA-L2: Image and Video Segmentation III: Edge or Color Segmentation TA-L3: Stereoscopic and 3D Processing III TA-L4: -

Soundproofing 101: a Presentation to the MCAC Environment and Health Subcommittee March 18, 2019 Content
Soundproofing 101: A presentation to the MCAC Environment and Health Subcommittee March 18, 2019 Content • Overview of How Logan Works • Noise Abatement Program • Soundproofing Regulatory Context • Soundproofing Process • History of the Program and Current Status • Questions/Discussion 2 The FAA uses Logan runways in combinations to safely and efficiently meet demand. Depending on which sets of runways the FAA chooses different communities are overflown Northeast Flow Southwest Flow R 4R\L and 9 R22R\L and 27 Northwest Flow Southeast Flow R33L\32 and 27 R33L\32 and 27 3 Because of Logan’s urban location, Massport has developed a comprehensive noise abatement program for Logan Airport • Noise abatement departure • 24/7 noise complaint line 617-561- procedures 3333 • Late night runway preference • State of the art Noise Monitoring opposite direction operations System • Decibel restriction on R4L • Near live flight tracking on website departures and 22R arrivals • http://www.massport.com/environment/environmental_rep orting/Noise%20Abatement/overview.aspx • Unidirectional/wind restriction use R14/32 • Soundproofing Program for Homes and School • Engine run-up restrictions • Limited time • Specific locations • Towing requirements for certain aircraft repositioning • Encourage use of single engine taxiing and reverse thrust 4 Noise Contours for environmental analysis and soundproofing must be created by using the FAA’s Airport Environmental Data Tool (AEDT) Model • The AEDT is an FAA Model • Critical inputs include number of flights, aircraft -
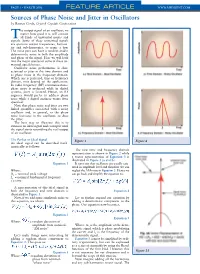
Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation
PAGE • MARCH 2006 FEATURE ARTICLE WWW.MPDIGEST.COM Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation he output signal of an oscillator, no matter how good it is, will contain Tall kinds of unwanted noises and signals. Some of these unwanted signals are spurious output frequencies, harmon- ics and sub-harmonics, to name a few. The noise part can have a random and/or deterministic noise in both the amplitude and phase of the signal. Here we will look into the major sources of some of these un- wanted signals/noises. Oscillator noise performance is char- acterized as jitter in the time domain and as phase noise in the frequency domain. Which one is preferred, time or frequency domain, may depend on the application. In radio frequency (RF) communications, phase noise is preferred while in digital systems, jitter is favored. Hence, an RF engineer would prefer to address phase noise while a digital engineer wants jitter specified. Note that phase noise and jitter are two linked quantities associated with a noisy oscillator and, in general, as the phase noise increases in the oscillator, so does the jitter. The best way to illustrate this is to examine an ideal signal and corrupt it until the signal starts resembling the real output of an oscillator. The Perfect or Ideal Signal Figure 1 Figure 2 An ideal signal can be described math- ematically as follows: The new time and frequency domain representation is shown in Figure 2 while a vector representation of Equation 3 is illustrated in Figure 3 (a and b.) Equation 1 It turns out that oscillators are usually satu- rated in amplitude level and therefore we can Where: neglect the AM noise in Equation 3. -

Don't Replace Your Windows. . .Soundproof Them. Reduce Noise
Don’t replace your windows. .Soundproof them. Reduce Noise Levels by 75% to 95%. Create REAL peace and quiet. What is it? A soundproof window is a second window placed behind your existing window that opens and closes just like your existing window. We do not remove or replace your existing window. Acoustically engineered to stop sound, it offers most of the benefits of dual-paned replacement windows and several benefits not available with replacement windows. o Absolutely Stops the Noise Reduces noise levels by 75% and more - much more than any dual-paned replacement window. You will be amazed how dramatic the improvement is!! oThe Best Insulation Available Our two window system provides better insulation than any one window system. Our windows insulate better than ANY dual-paned window. Simply the best insulating windows available - period! o Removes 99.9% of color-fading UV light Museum-quality protection for the harmful effects of UV light. Prevents the color-fading caused by ultraviolet light. UV light is often considered to be a health hazard that causes skin cancer and more. o Peace & Quiet - Lowered Stress - Better Health Stay home and enjoy "the peace and quiet of the countryside". Escape to the quiet surroundings of your own home, instead of only on weekend getaways and vacations. Noise causes restless sleep, higher stress levels, and can easily lead to hearing loss and other long-term health risks. More and more is being discovered about the harmful effects of even moderate noise levels in your home and work environment. ©2008 SOUNDPROOF WINDOWS, Inc. -

Results of the HARMONICA Project • Possible Links Between DYNAMAP and HARMONICA
HARMONICA PROJECT News tools to inform the public about environmental noise in cities and to assist decision-making www.noiseineu.eu DYNAMAP SPECIAL SESSION 22 International Conference on Sound and Vibration Florence 12-16 Jully 2015 OUTLINES • Brief overview of the noise observatory Bruitparif and the Île-de-France region • Results of the HARMONICA project • Possible links between DYNAMAP and HARMONICA Bruitparif, what is it? State • A collegiate association (NGO) representatives at the regional level • 100 members • Staff: 11 persons Environmental Infrastruture and consumer • 3 main objectives: and transport protection activities • Observation and evaluation associations • Support to public policies • Information and awareness Local authorities: cities, districts, region The Paris region « Ile-de- France » • 12 000 km2 • 12 million inhabitants • 40 000 km of roads • 1 800 km of railways • 3 main airports • 71% of inhabitants said they are annoyed by noise at home Need for a regional noise observatory to get reliable information on the noise levels in the Ile-de-France region Bruitparif was created in 2004 Map: Population density • END application that exceeds noise limit values • 20% of the population are exposed to noise levels that exceed the French limit values The LIFE HARMONICA Project HARMONICA = HARMOnised Noise Information for Citizens and Authorities • Co-funded over 3 years and 3 months (01/10/2011-31/12/2014) by EC • Two French non-profit associations specialised in the observation of environmental noise: • Coordinator : -

Teaching Fellow
Find more on our web: hipeac.net/jobs/12290 Trinity College Dublin Dublin, Ireland Teaching Fellow • Deadline: May 21, 2021 • Career levels: PostDoc • Keywords: Computer architecture, Embedded / Cyber-Physical Systems, Reconfigurable computing Trinity College Dublin Academic Posts Open We are delighted to invite applications for 2 academic posts at Trinity College with the Electronic Engineering Dept. (https://www.tcd.ie/eleceng/) in the School of Engineering. The appointments are in the area of Computational Engin- eering at the level of Asst Prof (€35,509 - €86,247, 4.5 years) and Teaching Fellow (€35,509 - €46,266, 2.5 years). Fur- ther information and applications for these posts are at jobs.tcd.ie (select Academic->Engineering). The positions are part of the new Human Capital Initiative supported by the Government of Ireland. Successful candid- ates will contribute to Computational Engineering research and teaching in the Department. This includes Signal Pro- cessing (Video, Audio, Climate), Communications, Biomedical Engineering, Media Technology and design of computa- tional hardware (FPGAs, ASICS for high throughput computation). The appointees will deliver courses in computation- al methodology including numerical software programming skills (NumPy, TensorFlow etc), computational science and engineering. The Department has a long history of strong collaboration with industry e.g. Google, YouTube, Qualcomm and is espe- cially strong in communications (connectcentre.ie) , DSP, audio/video processing (sigmedia.tv, adaptcentre.ie). The School runs a vibrant Biomedical Engineering initiative with contributions from each of the 3 disciplines including EEE. Please contact [email protected] if further context is required. Further information and applications for these posts are at jobs.tcd.ie (select Academic->Engineering). -

The Influence of Noise on Radio Signals from Cosmic Rays
The influence of noise on radio signals from cosmic rays Bachelor Thesis in Physics & Astronomy Katharina Holland Supervisor: Dr. Charles Timmermans Institute for Mathematics, Astrophysics and Particle Physics 1 Preface This thesis is the result of my Bachelor project. I have done my Bachelor project at the department of Experimental High Energy Physics of the Institute of Mathematics, Astrophysics and Particle Physics at the Radboud University of Nijmegen. I would like to thank Jose Coppens, Antje Fitzner, Stefan Grebe, Harm Schoor- lemmer and of course my supervisor Charles Timmermans for helping program- ming, answering questions and having a nice time. CONTENTS 2 Contents 1 Introduction 3 2 Cosmic rays & extensive air showers 3 3 Pierre Auger Observatory 5 4 Measurements in radio frequencies 7 4.1 Radio Detector . 7 4.2 Radiosignals . 7 5 Data 9 6 Analysis 11 6.1 Noise generation . 11 6.2 Generated noise added to a signal . 11 6.3 The variation of the original maximum by adding noise . 14 6.4 The effect of noise on the maximum . 17 6.5 The average and variation of the maximum as a function of SNR 20 6.6 Varying the size of the searching window . 23 6.7 Different noise generation . 26 6.8 Arrival direction reconstruction . 27 7 Conclusion 30 A Abbreviations 31 1 INTRODUCTION 3 1 Introduction When a cosmic ray enters the atmosphere, an extensive airshower starts. Billions of particles “rain“ on the Earth. At the Pierre Auger Observatory, there are several possibilities to detect extensive air showers. One of these possibilities is radio detection of cosmic rays.