DOCSLIB.ORG

Multifactor Capital Asset Pricing Model in the Jordanian Stock Market Mohammad Kamel Elshqirat Walden University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Multifactor Capital Asset Pricing Model in the Jordanian Stock Market Mohammad Kamel Elshqirat Walden University Walden University ScholarWorks Walden Dissertations and Doctoral Studies Walden Dissertations and Doctoral Studies Collection 2018 Multifactor Capital Asset Pricing Model in the Jordanian Stock Market Mohammad Kamel Elshqirat Walden University Follow this and additional works at: https://scholarworks.waldenu.edu/dissertations Part of the Finance and Financial Management Commons This Dissertation is brought to you for free and open access by the Walden Dissertations and Doctoral Studies Collection at ScholarWorks. It has been accepted for inclusion in Walden Dissertations and Doctoral Studies by an authorized administrator of ScholarWorks. For more information, please contact [email protected]. Walden University College of Management and Technology This is to certify that the doctoral dissertation by Mohammad Kamel Elshqirat has been found to be complete and satisfactory in all respects, and that any and all revisions required by the review committee have been made. Review Committee Dr. Mohammad Sharifzadeh, Committee Chairperson, Management Faculty Dr. Robert DeYoung, Committee Member, Management Faculty Dr. Craig Barton, University Reviewer, Management Faculty Chief Academic Officer Eric Riedel, Ph.D. Walden University 2018 Abstract Multifactor Capital Asset Pricing Model in the Jordanian Stock Market by Mohammad Kamel Elshqirat MA, Hashemite University, 2007 BS, University of Jordan, 1998 Dissertation Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Management Walden University May 2018 Abstract A valid and accurate capital asset pricing model (CAPM) may help investors and mutual funds managers in determining expected returns and thus, may increase profits which can be reflected on the community resources. The problem is that the traditional CAPM does not accurately predict the expected rate of return. A more accurate model is needed to help investors in determining the intrinsic price of the financial asset they want to sell or buy. The purpose of this study was to examine the validity of the single-factor CAPM and then develop and test the validity of a multifactor CAPM in the Jordanian stock market. The study was informed by the modern portfolio theory and specifically by the single-factor CAPM developed by Sharpe, Lintner, and Mossin. The research questions for the study examined the factors that may explain the variation in the expected rate of return on stocks in the Jordanian stock market and the relationship between the expected rate of return and factors of market return, company size, financial leverage, and operating leverage. A causal-comparative quantitative research design was employed to achieve the purpose of the study by testing the listed companies on the Amman stock exchange (ASE) for the period from 2000 to 2015. Data were collected from the ASE database and analyzed using the multiple regression model and t test. The results revealed that market return, company size, and financial leverage are not predictors of the expected rate of return while operating leverage is a predictor. The results of this study may contribute to positive social change by changing the way the individual investors and mutual funds managers select their investing portfolios which can lead to better resource distribution in the economy. Multifactor Capital Asset Pricing Model and the Jordanian Stock Market by Mohammad Kamel Elshqirat MA, Hashemite University, 2007 BS, University of Jordan, 1998 Dissertation Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Management Walden University May 2018 Dedication This dissertation is dedicated to my mother and father who spent most of their life and money in helping me and my brothers to complete our education. Special dedication is to my father who spared no effort to provide me with medical treatment after I suffered from a serious injury when I was a child. I am thankful for all my brothers who supported me during my study. My thanks also go to those people who treated me bad during my career because they pushed me to work harder and prove myself. Acknowledgments I am grateful for Walden University and for all of its faculty members and staff. I want to thank all faculty members of management for everything I learned from them during my coursework. Special thanks go to Dr. Sharifzadeh for accepting to be my chair and for all of his recommendations and directions. In addition, I want to thank Dr. DeYoung, my committee member, for his helpful recommendations on my writing. Finally, I am thankful for all Jordanian agencies that provide the public with data about the Jordanian economy and stock market. Table of Contents List of Tables .......................................................................................................................v List of Figures ................................................................................................................... vii Chapter 1: Introduction to the Study ....................................................................................1 Background of the Study ...............................................................................................2 Problem Statement .........................................................................................................5 Purpose of the Study ......................................................................................................6 Research Questions and Hypotheses .............................................................................6 Research Questions ................................................................................................. 6 Research Hypotheses .............................................................................................. 7 Theoretical Foundation ................................................................................................12 Nature of the Study ......................................................................................................14 Definitions....................................................................................................................15 Assumptions .................................................................................................................17 Scope and Delimitations ..............................................................................................19 Limitations ...................................................................................................................20 Significance of the Study .............................................................................................20 Significance to Theory .......................................................................................... 20 Significance to Practice......................................................................................... 21 Significance to Social Change .............................................................................. 22 Summary and Transition ..............................................................................................23 Chapter 2: Literature Review .............................................................................................25 i Literature Search Strategy............................................................................................26 Literature Review through Annotated Bibliographies .......................................... 26 Libraries, Databases, Search Engines, and Search Terms Used ........................... 26 Scope of the Reviewed Literature ......................................................................... 27 Capital Asset Pricing Model ........................................................................................28 Theoretical Analysis of CAPM ............................................................................. 28 CAPM Extensions ................................................................................................. 42 Arbitrage Pricing Theory .............................................................................................44 Empirical Tests of CAPM ............................................................................................46 Size, Operating Leverage, and Financial Leverage .....................................................47 Summary and Conclusions ..........................................................................................49 Chapter 3: Research Method ..............................................................................................52 Introduction ..................................................................................................................52 Research Design and Rationale ...................................................................................52 Methodology ................................................................................................................54 Population and Sampling Procedures ................................................................... 54 Pilot Study ............................................................................................................. 56 Data Collection ..................................................................................................... 57 Study Variables ............................................................................................................57 Study Hypotheses.........................................................................................................60
Load more

Recommended publications
  • The Role of MENA Stock Exchanges in Corporate Governance the Role of MENA Contents Stock Exchanges Executive Summary Introduction in Corporate Governance Part I
    The Role of MENA Stock Exchanges in Corporate Governance The Role of MENA Contents Stock Exchanges Executive Summary Introduction in Corporate Governance Part I. Key Features of MENA Markets Dominant state ownership Low regional and international integration Moderate competition for listings Young markets, dominated by a few sectors High levels of retail investment Diversifi cation of fi nancial products Part II. The Role of Exchanges in Corporate Governance The regulatory role The listing authority Corporate governance codes Disclosure and transparency The enforcement powers Concluding Remarks Annex I. About The Taskforce Annex II. Consolidated Responses to the OECD Questionnaire Annex III. Largest Listed Companies in the MENA region www.oecd.org/daf/corporateaffairs/mena Photos on front cover : © Media Center/Saudi Stock Exchange (Tadawul) and © Argus/Shutterstock.com 002012151cov.indd 1 12/06/2012 12:48:57 The Role of MENA Stock Exchanges in Corporate Governance This work is published on the responsibility of the Secretary-General of the OECD. The opinions expressed and arguments employed herein do not necessarily reflect the official views of the Organisation or of the governments of its member countries. This document and any map included herein are without prejudice to the status of or sovereignty over any territory, to the delimitation of international frontiers and boundaries and to the name of any territory, city or area. © OECD 2012 You can copy, download or print OECD content for your own use, and you can include excerpts from OECD publications, databases and multimedia products in your own documents, presentations, blogs, websites and teaching materials, provided that suitable acknowledgement of OECD as source and copyright owner is given.
    [Show full text]
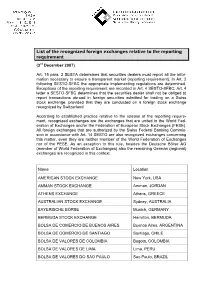
  • List of the Recognized Foreign Exchanges Relative to the Reporting Requirement (3Rd December 2007)
    List of the recognized foreign exchanges relative to the reporting requirement (3rd December 2007) Art. 15 para. 2 SESTA determines that securities dealers must report all the infor- mation necessary to ensure a transparent market (reporting requirement). In Art. 2 following SESTO-SFBC the appropriate implementing regulations are determined. Exceptions of the reporting requirement are recorded in Art. 4 SESTO-SFBC. Art. 4 letter a SESTO-SFBC determines that the securities dealer shall not be obliged to report transactions abroad in foreign securities admitted for trading on a Swiss stock exchange, provided that they are conducted on a foreign stock exchange recognized by Switzerland. According to established practice relative to the release of the reporting require- ment, recognized exchanges are the exchanges that are united in the World Fed- eration of Exchanges and/or the Federation of European Stock Exchanges (FESE). All foreign exchanges that are authorized by the Swiss Federal Banking Commis- sion in accordance with Art. 14 SESTO are also recognized exchanges concerning this matter, even they are neither member of the World Federation of Exchanges nor of the FESE. As an exception to this rule, besides the Deutsche Börse AG (member of World Federation of Exchanges) also the remaining German (regional) exchanges are recognized in this context. Name Location AMERICAN STOCK EXCHANGE New York, USA AMMAN STOCK EXCHANGE Amman, JORDAN ATHENS EXCHANGE Athens, GREECE AUSTRALIAN STOCK EXCHANGE Sydney, AUSTRALIA BAYERISCHE BÖRSE Munich, GERMANY BERMUDA STOCK EXCHANGE Hamilton, BERMUDA BOLSA DE COMERCIO DE BUENOS AIRES Buenos Aires, ARGENTINA BOLSA DE COMERCIO DE SANTIAGO Santiago, CHILE BOLSA DE VALORES DE COLOMBIA Bogota, COLOMBIA BOLSA DE VALORES DE LIMA Lima, PERU BOLSA DE VALORES DO SAO PAULO Sao Paulo, BRAZIL Name Location BOLSA MEXICANA DE VALORES Mexico, MEXICO BOLSAS Y MERCADOS ESPANOLES Barcelona, Bilbao, Madrid, Valencia, SPAIN BOMBAY STOCK EXCHANGE LTD.
    [Show full text]
  • The Effect of Conflict on Palestine, Israel, and Jordan Stock Markets
    International Review of Economics and Finance 56 (2018) 258–266 Contents lists available at ScienceDirect International Review of Economics and Finance journal homepage: www.elsevier.com/locate/iref The effect of conflict on Palestine, Israel, and Jordan stock markets Islam Hassouneh a,*, Anabelle Couleau b, Teresa Serra b, Iqbal Al-Sharif a a College of Administrative Science and Informatics, Palestine Polytechnic University (PPU), P.O. Box 198, Abu Ruman, Hebron, Palestine b Department of Agricultural and Consumer Economics, University of Illinois, 335 Mumford Hall, 1301 W Gregory Drive, Urbana, IL 61801, United States ARTICLE INFO ABSTRACT JEL classification: This research studies how the Israeli-Palestinian conflict affects Palestine, Israel and Jordan stock C32 markets, as well as the links between these markets on a daily basis. A violence index is built and G11 used as an exogenous variable in a VECM-MGARCH model. Our findings suggest the existence of G15 an equilibrium relationship between the three markets, which is essentially kept through Pales- tinian and Jordanian stock market adjustments and that does not respond to increases in violence. Keywords: An increase in violence has short-run direct negative impacts on the Palestinian stock exchange, Stock markets but does not directly influence the Israeli and Jordanian stock markets. Volatility VECM MGARCH model 1. Introduction Understanding the dynamic relationships between different stock markets sheds light on important financial market characteristics, and provides valuable information
    [Show full text]
  • Report of the 5 Th Meeting
    FIFTH MEETING OF THE OIC MEMBER STATES’ STOCK EXCHANGES FORUM FINAL REPORT OF THE FIFTH MEETING OF THE OIC MEMBER STATES’ STOCK EXCHANGES FORUM ISTANBUL, SEPTEMBER 17-18, 2011 The Marmara Hotel Istanbul, September 2011 1 FINAL REPORT OF THE FIFTH MEETING OF THE OIC MEMBER STATES’ STOCK EXCHANGES FORUM ISTANBUL, SEPTEMBER 17-18, 2011 The Marmara Hotel Istanbul, September 2011 2 TABLE OF CONTENTS Final Report of the Fifth Meeting of the OIC Member States’ Stock Exchanges Forum ANNEXES I. Presentation by Mr. Thomas Krabbe II. Presentation by Mr. Roland Bellegarde III. Presentation by Mr. Lauri Rosendahl IV. Presentation by Mr. Stephan Pouyat V. Presentation by Mr. Philippe Carré VI. Presentation by Mr. Rushdi Siddiqui on behalf of Thomson Reuters VII. Presentation by Mr. Ibrahim Idjarmizuan on behalf of IFSB VIII. Presentation by Mr. Gürsel Kona from the Istanbul Stock Exchange IX. Presentation by Mr. Ijlal Alvi on behalf of IIFM X. Presentation by Avşar Sungurlu, on behalf of BMD Securities Inc. XI. Presentation by Mr. Hüseyin Erkan, as Forum Chairman XII. Presentation by Şenay Pehlivanoğlu on behalf of the Task Force for Customized Indices and Exchange Traded Islamic Financial Products XIII. Presentation by Mr. Charbel Azzi on behalf of S&P Indices XIV. Presentation by Dr. Eralp Polat on behalf of the Forum Secretariat XV. Presentation by Mr. Abolfazl Shahrabadi and Mr. Hamed Soltaninejad on behalf of the Task Force for Capital Market Linkages 3 FINAL REPORT OF THE FFIFTH MEETING OF THE OIC MEMBER STATES’ STOCK EXCHANGES FORUM ISTANBUL, SEPTEMBER 17-18, 2011 4 Original: English FINAL REPORT OF THE FIFTH MEETING OF THE OIC MEMBER STATES’ STOCK EXCHANGES FORUM (Istanbul, September 17-18, 2011) 1.
    [Show full text]
  • Amman Stock Exchange Amman Stock Exchange
    Amman Stock Exchange Amman Stock Exchange Annual Report 2015 His Majesty King Abdullah II Ibn Al Hussein His Royal Highness Crown Prince Al Hussein Bin Abdullah II The Amman Stock Exchange (ASE) was established in March 11, 1999 as an independent institution authorized to function as an exchange for the trading of securities in Jordan under the Securities Law, No. 23 of 1997 and its amendments. The ASE has a legal personality with financial and administrative autonomy and it is regulated by Jordan Securities Commission. Vision Advanced financial market distinguished legislatively and technically, regionally and globally; rising to the latest international standards in the field of financial markets to provide an attractive investment environment. Mission Provide an organized, fair, transparent, and efficient market for trading securities in Jordan, and secure a safe environment for trading securities to deepen trust in the stock market therefore to serve the national economy. Objectives • Creating an attractive, safe, competitive, transparent and credible investment environment. • Developing processes, methods, and systems for trading securities in the stock market according to the latest international standards. • Developing and delivering an outstanding service to the related parties. • Disseminating trading information to the largest possible number of traders and interested parties. • Enhance the public awareness of all segments of society, while devoting especial attention to traders of securities. • Increasing the depth and the transparency of the ASE and diversifying the financial instruments available to investors. • Enhancing the cooperation with the Arab, regional and international exchanges, organizations and federations. Amman Stock Exchange 7 Amman Stock Exchange Contents Subject Page Chairman’s Statement............................................................................
    [Show full text]
  • The List of Approved Stock Exchanges
    November 9, 2018 The following stock exchanges are approved by the Cayman Islands Monetary Authority for purposes of the Regulatory Laws pursuant to the Authority’s Regulatory Policy – Approved Stock Exchanges. Note: This list is for illustrative purposes only and is subject to change. To verify whether a stock exchange is approved by the Cayman Islands Monetary Authority, please refer to the Regulatory Policy – Approved Stock Exchanges. Amman Stock Exchange Deutsche Borse Athens Exchange Dusseldorf Stock Exchange Australian Securities Exchange EDX London Barbados Stock Exchange Eurex BATS Exchange Euronext Bayerische Borse AG Fukuoka Stock Exchange* Berlin Stock Exchange Gibraltar Stock Exchange Bermuda Stock Exchange Hong Kong Exchange and Clearing BM&F Bovespa Indonesia Stock Exchange BME Spanish Exchanges Intercontinental Exchange BOAG Borsen AG International Securities Exchange Bolsa de Comercio de Buenos Aires Irish Stock Exchange Bolsa de Comercio de Santiago Istanbul Stock Exchange Bolsa de Valores de Caracas* Jamaica Stock Exchange Bolsa de Valores de Colombia JASDAQ Bolsa de Valores de Lima Johannesburg Stock Exchange Bombay Stock Exchange Korea Stock Exchange Borsa Italiana SPA London Stock Exchange Bratislava Stock Exchange Ljubljana Stock Exchange Bucharest Stock Exchange Luxembourg Stock Exchange Budapest Stock Exchange Madrid Stock Exchange Bulgarian Stock Exchange Malaysia Stock Exchange Cayman Islands Stock Exchange Malta Stock Exchange Channel Islands Stock Exchange* Mexican Stock Exchange Chicago Board Options Exchange
    [Show full text]
  • Market Closures and Restrictions (As of June 22, 2020 12:00 P.M
    Market Closures and Restrictions (As of June 22, 2020 12:00 p.m. EDT) Country Restrictions Source Information United States of . Electronic trading. Starting March 23, 2020, the New York Stock NYSE To Temporarily Close Floor, Move To Electronic America Exchange (NYSE) will temporarily close its trading floor and move Trading After Positive Coronavirus Tests fully to electronic trading. The facilities to be closed are the NYSE Cboe Options Exchange Temporarily Shift to Fully equities trading floor and NYSE American Options trading floor in Electronic Trading New York, and the NYSE Arca Options trading floor in San The NYSE Will Reopen the Trading Floor Francisco. The CME Group temporarily closed its Chicago trading floor as of the close of business on March 13, 2020. Cboe temporarily moved to electronic trading effective on March 16, 2020. NYSE President Stacey Cunningham announced in an opinion piece posted by the Wall Street Journal the plan to reopen the NYSE trading floor on May 26 with numerous restrictions. Austria . Restrictions on short selling. The Austrian Financial Market Authority Austria's Financial Markets Watchdog Bans Short-Selling (FMA) temporarily prohibited the short selling of certain financial Until April 18 instruments on the Vienna stock exchange until April 18, 2020. The FMA Extends Ban on Short Selling of Certain Financial ban includes creating or increasing net short positions via derivatives Instruments Listed on Vienna Stock Exchange, While or other financial instruments which confer a financial advantage in Also Modifying It the event of a decrease in the price of covered stocks. Short sales of equity indices or baskets are covered by the ban if the restricted securities account for 50% or more of their composition.
    [Show full text]
  • Annual Report 2005 Amman Stock Exchange Amman-The Hashemite Kingdom of Jordan
    Amman Stock Exchange ANNUAL REPO RT 200 5 Amman Stock Exchange ANNUAL REPORT 2005 His Majesty King Abdullah, II Bin Al-Hussein AAmmanmman SStoctock ExExchange ANNUAUAL REPORTRT 2005 BOARD OF DIRECTORS H.E. Mohammed S. Hourani Chairman Mr. Mansour Haddadin Vice Chairman Dr. Abdul-Hadi Alaween Member Mr. Adnan Madi Member Jordan Islamic Bank for Finance and Investment Mr. Saqer Abdul-Fattah Member The Housing Bank for Trade and Finance Mr. Jawad Kharoof Member Al-Amal Investment Mr. Younes Qawasmi Member Aman for Securities Mr. Jalil Tarif Chief Executive Officer Amman Stock Exchange ANNUAL REPORT 2005 CONTENTS Subject Page Chairmanʼs Statement 9 Economic Situation 13 Arab And International Stock Exchanges 15 The ASE Performance In 2005 21 The ASE Accomplishments During The Year 2005 31 Financial Statements 41 Statistical Appendix 61 Amman Stock Exchange ANNUAL REPORT 2005 CHAIRMANʼS STATEMENT Honorable Members of the General Assembly of the Amman Stock Exchange, On behalf of myself and my colleagues, the members of the Board of Directors, it is my pleasure to present to you the ASEʼs Seventh Annual Report, which highlights ASEʼs most significant achievements for the year 2005, and its future perspectives and plans for the year 2006. The year 2005 witnessed an increasing activity at the ASE, and it was the best in terms of ASEʼs performance indicators since the establishment of the securities market in Jordan, which contributed to increased the interest in the ASE on both the local and the international levels. The price index at the ASE rose by 93% and trading volume increased by many folds during 2005 to reach JD16.9 billion.
    [Show full text]
  • Join Us in Celebrating International Women’S Day March 8, 2021 RING the BELL for GENDER EQUALITY
    Join us in Celebrating International Women’s Day March 8, 2021 RING THE BELL FOR GENDER EQUALITY A Call To Action For Businesses Everywhere To Take Concrete Actions To Advance Women’s Empowerment And Gender Equality Celebrate International Women’s Day Ring the Bell for Gender Equality 7th Annual “Ring the Bell for Objectives: Gender Equality” Ceremony • Raise awareness of the importance of private sector action To celebrate International Women’s Day (8 March), to advance gender equality, and showcase existing examples Exchanges around the world will be invited to be to empower women in the workplace, marketplace and part of a global event on gender equality by hosting community a bell ringing ceremony – or a virtual event– to • Convene business leaders, investors, government, civil help raise awareness for women’s economic society and other key partners at the country- and regional empowerment. level to highlight the business case for gender equality • Encourage business to take action to advance the Sustainable Development Goals (SDGs) and promote uptake of the Women’s Empowerment Principles (WEPs) • Highlight how exchanges can help advance the SDGs by promoting gender equality VIRTUAL OPTION: Please note that given the current COVID-19 crisis, if in person ceremonies are not possible, partners are welcome to host a virtual event on the online platform we will use to organize a virtual global Ring the Bell for Gender Equality event this year. Be Part of a Global Effort In March 2020, 77 exchanges rang their bells for gender equality —
    [Show full text]
  • Over 100 Exchanges Worldwide 'Ring the Bell for Gender Equality in 2021' with Women in Etfs and Five Partner Organizations
    OVER 100 EXCHANGES WORLDWIDE 'RING THE BELL FOR GENDER EQUALITY IN 2021’ WITH WOMEN IN ETFS AND FIVE PARTNER ORGANIZATIONS Wednesday March 3, 2021, London – For the seventh consecutive year, a global collaboration across over 100 exchanges around the world plan to hold a bell ringing event to celebrate International Women’s Day 2021 (8 March 2020). The events - which start on Monday 1 March, and will last for two weeks - are a partnership between IFC, Sustainable Stock Exchanges (SSE) Initiative, UN Global Compact, UN Women, the World Federation of Exchanges and Women in ETFs, The UN Women’s theme for International Women’s Day 2021 - “Women in leadership: Achieving an equal future in a COVID-19 world ” celebrates the tremendous efforts by women and girls around the world in shaping a more equal future and recovery from the COVID-19 pandemic. Women leaders and women’s organizations have demonstrated their skills, knowledge and networks to effectively lead in COVID-19 response and recovery efforts. Today there is more recognition than ever before that women bring different experiences, perspectives and skills to the table, and make irreplaceable contributions to decisions, policies and laws that work better for all. Women in ETFs leadership globally are united in the view that “There is a natural synergy for Women in ETFs to celebrate International Women’s Day with bell ringings. Gender equality is central to driving the global economy and the private sector has an important role to play. Our mission is to create opportunities for professional development and advancement of women by expanding connections among women and men in the financial industry.” The list of exchanges and organisations that have registered to hold an in person or virtual bell ringing event are shown on the following pages.
    [Show full text]
  • The Role of MENA Stock Exchanges in Corporate Governance the Role of MENA Contents Stock Exchanges Executive Summary Introduction in Corporate Governance Part I
    The Role of MENA Stock Exchanges in Corporate Governance The Role of MENA Contents Stock Exchanges Executive Summary Introduction in Corporate Governance Part I. Key Features of MENA Markets Dominant state ownership Low regional and international integration Moderate competition for listings Young markets, dominated by a few sectors High levels of retail investment Diversifi cation of fi nancial products Part II. The Role of Exchanges in Corporate Governance The regulatory role The listing authority Corporate governance codes Disclosure and transparency The enforcement powers Concluding Remarks Annex I. About The Taskforce Annex II. Consolidated Responses to the OECD Questionnaire Annex III. Largest Listed Companies in the MENA region www.oecd.org/daf/corporateaffairs/mena Photos on front cover : © Media Center/Saudi Stock Exchange (Tadawul) and © Argus/Shutterstock.com 002012151cov.indd 1 12/06/2012 12:48:57 The Role of MENA Stock Exchanges in Corporate Governance This work is published on the responsibility of the Secretary-General of the OECD. The opinions expressed and arguments employed herein do not necessarily reflect the official views of the Organisation or of the governments of its member countries. This document and any map included herein are without prejudice to the status of or sovereignty over any territory, to the delimitation of international frontiers and boundaries and to the name of any territory, city or area. © OECD 2012 You can copy, download or print OECD content for your own use, and you can include excerpts from OECD publications, databases and multimedia products in your own documents, presentations, blogs, websites and teaching materials, provided that suitable acknowledgement of OECD as source and copyright owner is given.
    [Show full text]
  • Dow Jones Middle East Indices Methodology
    Dow Jones Middle East Indices Methodology June 2021 S&P Dow Jones Indices: Index Methodology Table of Contents Introduction 3 Index Objective 3 Index Family and Highlights 3 Supporting Documents 4 Eligibility Criteria and Index Construction 5 Index Eligibility 5 Ineligible Securities 5 Multiple Classes of Stock 5 Index Calculations 5 Index Construction 6 Dow Jones GCC Index and Dow Jones GCC Ex-Saudi Index 6 Dow Jones MENA Index and Dow Jones MENA Ex-Saudi Index 7 Index Maintenance 8 Rebalancing 8 Additions 8 Deletions 8 Corporate Actions 9 Currency of Calculation and Additional Index Return Series 9 Investable Weight Factor (IWF) 9 Other Adjustments 9 Base Dates and History Availability 10 Index Data 11 Calculation Return Types 11 Index Governance 12 Index Committee 12 S&P Dow Jones Indices: Dow Jones Middle East Indices Methodology 1 Index Policy 13 Announcements 13 Pro-forma Files 13 Holiday Schedule 13 Rebalancing 14 Unexpected Exchange Closures 14 Recalculation Policy 14 Real-Time Calculation 14 Contact Information 14 Index Dissemination 15 Tickers 15 Index Data 15 Web site 15 Appendix I 16 Methodology Changes 16 Appendix II 17 EU Required ESG Disclosures 17 Disclaimer 18 S&P Dow Jones Indices: Dow Jones Middle East Indices Methodology 2 Introduction Index Objective The Dow Jones Middle East Indices are comprehensive, rules-based indices that measure the performance of Middle East stock markets. The indices reflect the available float-adjusted market capitalization (FMC) defined by the foreign investment limits applicable to Gulf Cooperation Council (GCC) residents (for the applicable GCC countries), which is typically larger than that available to foreigners.
    [Show full text]