Reducing Redundancy in Data Organization and Arithmetic Calculation for Stencil Computations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SIGOPS Annual Report 2012
SIGOPS Annual Report 2012 Fiscal Year July 2012-June 2013 Submitted by Jeanna Matthews, SIGOPS Chair Overview SIGOPS is a vibrant community of people with interests in “operatinG systems” in the broadest sense, includinG topics such as distributed computing, storaGe systems, security, concurrency, middleware, mobility, virtualization, networkinG, cloud computinG, datacenter software, and Internet services. We sponsor a number of top conferences, provide travel Grants to students, present yearly awards, disseminate information to members electronically, and collaborate with other SIGs on important programs for computing professionals. Officers It was the second year for officers: Jeanna Matthews (Clarkson University) as Chair, GeorGe Candea (EPFL) as Vice Chair, Dilma da Silva (Qualcomm) as Treasurer and Muli Ben-Yehuda (Technion) as Information Director. As has been typical, elected officers agreed to continue for a second and final two- year term beginning July 2013. Shan Lu (University of Wisconsin) will replace Muli Ben-Yehuda as Information Director as of AuGust 2013. Awards We have an excitinG new award to announce – the SIGOPS Dennis M. Ritchie Doctoral Dissertation Award. SIGOPS has lonG been lackinG a doctoral dissertation award, such as those offered by SIGCOMM, Eurosys, SIGPLAN, and SIGMOD. This new award fills this Gap and also honors the contributions to computer science that Dennis Ritchie made durinG his life. With this award, ACM SIGOPS will encouraGe the creativity that Ritchie embodied and provide a reminder of Ritchie's leGacy and what a difference a person can make in the field of software systems research. The award is funded by AT&T Research and Alcatel-Lucent Bell Labs, companies that both have a strong connection to AT&T Bell Laboratories where Dennis Ritchie did his seminal work. -

2020 SIGACT REPORT SIGACT EC – Eric Allender, Shuchi Chawla, Nicole Immorlica, Samir Khuller (Chair), Bobby Kleinberg September 14Th, 2020
2020 SIGACT REPORT SIGACT EC – Eric Allender, Shuchi Chawla, Nicole Immorlica, Samir Khuller (chair), Bobby Kleinberg September 14th, 2020 SIGACT Mission Statement: The primary mission of ACM SIGACT (Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory) is to foster and promote the discovery and dissemination of high quality research in the domain of theoretical computer science. The field of theoretical computer science is the rigorous study of all computational phenomena - natural, artificial or man-made. This includes the diverse areas of algorithms, data structures, complexity theory, distributed computation, parallel computation, VLSI, machine learning, computational biology, computational geometry, information theory, cryptography, quantum computation, computational number theory and algebra, program semantics and verification, automata theory, and the study of randomness. Work in this field is often distinguished by its emphasis on mathematical technique and rigor. 1. Awards ▪ 2020 Gödel Prize: This was awarded to Robin A. Moser and Gábor Tardos for their paper “A constructive proof of the general Lovász Local Lemma”, Journal of the ACM, Vol 57 (2), 2010. The Lovász Local Lemma (LLL) is a fundamental tool of the probabilistic method. It enables one to show the existence of certain objects even though they occur with exponentially small probability. The original proof was not algorithmic, and subsequent algorithmic versions had significant losses in parameters. This paper provides a simple, powerful algorithmic paradigm that converts almost all known applications of the LLL into randomized algorithms matching the bounds of the existence proof. The paper further gives a derandomized algorithm, a parallel algorithm, and an extension to the “lopsided” LLL. -
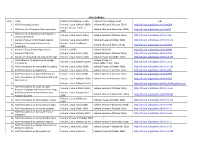
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1 (March 1969) Volume 49 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J204 Volume 24 Issue 1 (Feb. 1, 2. ACM Journal of Computer Documentation Volume 26 Issue 4 (November 2002) http://dl.acm.org/citation.cfm?id=J24 2000) ACM Journal on Emerging Technologies in 3. Volume 1 Issue 1 (April 2005) Volume 13 Issue 2 (October 2016) http://dl.acm.org/citation.cfm?id=J967 Computing Systems 4. Journal of Data and Information Quality Volume 1 Issue 1 (June 2009) Volume 8 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1191 Journal on Educational Resources in Volume 1 Issue 1es (March 5. Volume 16 Issue 2 (March 2016) http://dl.acm.org/citation.cfm?id=J814 Computing 2001) 6. Journal of Experimental Algorithmics Volume 1 (1996) Volume 21 (2016) http://dl.acm.org/citation.cfm?id=J430 7. Journal of the ACM Volume 1 Issue 1 (Jan. 1954) Volume 63 Issue 4 (October 2016) http://dl.acm.org/citation.cfm?id=J401 8. Journal on Computing and Cultural Heritage Volume 1 Issue 1 (June 2008) Volume 9 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J1157 ACM Letters on Programming Languages Volume 2 Issue 1-4 9. Volume 1 Issue 1 (March 1992) http://dl.acm.org/citation.cfm?id=J513 and Systems (March–Dec. 1993) 10. ACM Transactions on Accessible Computing Volume 1 Issue 1 (May 2008) Volume 9 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1156 11. -

Turbulent Flame Propagation Through Non-Homogeneous Reactant
MAHMUT TAYLAN KANDEMIR Assoc. Prof. of Computer Science and Engineering Department The Pennsylvania State University 354C IST Building, University Park, PA 16802, USA Phone: (814) 863-4888 Fax: (814) 865-3176 Email: [email protected] Web: http://www.cse.psu.edu/~kandemir Education and Training Istanbul Technical University, Turkey Computer Engineering B.S. 1988 Istanbul Technical University, Turkey Computer Engineering M.S. 1992 Syracuse University, NY, USA Computer Science Ph.D. 1999 Research and Professional Experience 9/04 - present Associate Professor, Computer Science and Engineering, Pennsylvania State University 9/99 - 9/04 Assistant Professor, Computer Science and Engineering, Pennsylvania State University 9/97 - 9/99 Visiting Ph.D. Student, ECE Department, Northwestern University 9/95 - 9/97 Teaching Assistant, EECS Department, Syracuse University Research Interests Optimizing Compilers, Parallel I/O and Storage Systems, High-Performance Computing, Energy-Aware System Design, and Reliable Computing. Teaching Interests Compilers, Programming Languages, High-Level Synthesis and Multicore Architectures. Awards and Honors Outstanding Research Award, Penn State Engineering Society (PSES), 2004 Top Download from ACM’s Digital Library (October 2006) Best Paper Award in IPDPS, 2008 Best Paper Award in ICPADS, 2006 Best Paper Award in Compiler Construction Conference, 2002 Best Paper Nominations in DAC 2004, DAC 2005, DAC 2006 Editorship 2006-present Associate Editor, International Journal of Distributed Sensor Networks 2004-present -

Lori L. Pollock January 2016 Personal Data Research Interests Education
Vita Lori L. Pollock January 2016 Personal Data Address: Dept. of Computer and Information Sciences 436 Smith Hall University of Delaware Newark, DE 19716 Phone: 302 831-1953 Email: [email protected] Research Interests Software analysis, software testing, green software engineering, software maintenance tools, compiler optimization for parallel architectures, computer science education. Education Ph.D. Computer Science, April 1986, University of Pittsburgh, Pittsburgh, PA Dissertation: An approach to incremental compilation of optimized code Advisor: Mary Lou Soffa M.S. Computer Science, August 1983, University of Pittsburgh B.S. Computer Science, magna cum laude, June 1981, Allegheny College, Meadville, PA B.S. Economics, magna cum laude, June 1981, Allegheny College, Meadville, PA Professional Experience September 2004 to present: Professor, Department of Computer and Information Sciences, University of Delaware. September 2012 to May 2013: Research Consultant, ABB Inc. September 1998 to 2003: Associate Professor, Department of Computer and Information Sciences, University of Delaware. September 1998 to May 1999, September 2012 to August 2013: Research Consultant, Army Research Laboratory, Aberdeen, MD. September 1992 to September 1998: Assistant Professor, Department of Computer and Information Sciences, University of Delaware. June-August, 1993 and 1994: Research Scientist, Supercomputing Research Center, Bowie, MD. September 1991 to August 1992: Visiting Assistant Professor, Department of Computer and Information Sciences, University of Delaware. 1 January 1986 to May 1990: Assistant Professor, Department of Computer Science, Rice University. September 1982 to September 1984: Teaching assistant and Instructor, Department of Computer Science, University of Pittsburgh. June-August 1982: Programmer, Hagerstown Cash Register, Inc., Hagerstown, MD. Honors and Awards Invited Keynote Speaker, 3rd International Workshop on Software Engineering Research and Industrial Practice (SER&IP 2016) at ICSE, 2016. -

Personal Research Interests Positions, Education, and Academic Degrees
Pavel Veselý Curriculum Vitae Personal Current position: Assistant Professor at Computer Science Institute of Charles University Address: Charles University Faculty of Mathematics and Physics Computer Science Institute Malostranské nám. 25, 118 00 Praha 1, Czech Republic Email: [email protected] Web page: http://iuuk.mff.cuni.cz/~vesely/ ORCID: 0000-0003-1169-7934 DBLP: dblp.uni-trier.de/pers/hd/v/Vesel=yacute=:Pavel Google Scholar: scholar.google.cz/citations?user=65ss5RMAAAAJ Research Interests Theoretical computer science and combinatorics, with particular focus on designing ecient algorithms and data structures, specically: streaming algorithms (quantile estimation, geometric streams, packing and scheduling problems), online algorithms (buer management, packing and scheduling problems), and approximation algorithms. Positions, Education, and Academic Degrees September 2020 present: Assistant Professor, Computer Science Institute of Charles University, Prague, Czech Republic. On leave from 19 September 2020 30 April 2021. September 2018 April 2021: Research Fellow, Department of Computer Science, University of Warwick. Adviser prof. Graham Cormode. PhD. 2018, Charles University, doctoral thesis Online Algorithms for Packet Scheduling. Supervisor prof. RNDr. Ji°í Sgall, DrSc. October 2014 September 2018: PhD studies at Computer Science Institute of Charles University, Prague, Czech Republic. Supervisor prof. RNDr. Ji°í Sgall, DrSc. Mgr. 2014, Charles University, master thesis Online algorithms for variants of bin packing. Supervisor prof. RNDr. Ji°í Sgall, DrSc. October 2012 September 2014: master studies, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic. Bc. 2012, Charles University, bachelor thesis Articial intelligence in abstract 2-player games. Supervisor RNDr. Tomá² Valla, Ph.D. October 2010 September 2012: bachelor studies, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic. -

Professor Shang-Hua Teng
Professor Shang-Hua Teng Department of Computer Science, University of Southern California 1039 25 Street 3710 McClintock, RTH 505, Los Angeles, CA 90089 Santa Monica, CA 90403 (213) 740-3667, [email protected] (617) 440-4281 EMPLOYMENT: University Professor USC (2017 – ) Seeley G. Mudd Professor (Computer Science and Mathematics) USC (2012 – ) Chair and Seeley G. Mudd Professor (Computer Science) USC (2009 – 2012) Professor (Computer Science) Boston University (2002 – 2009) Research Affiliate Professor (Mathematics) MIT (1999 – Present) Visiting Research Scientist Microsoft Research Asia and New England (2004 – Present) Senior Research Scientist Akamai (1997 – 2009) Visiting Professor (Computer Science) Tsinghua University (2004 – 2008) Professor (Computer Science)[Associate Professor before 1999] UIUC (2000 – 2002) Research Scientist IBM Almaden Research Center (1997 – 1999) Assistant Professor (Computer Science) Univ. of Minnesota (1994 – 1997) Research Scientist Intel Corporation (Summer 1994, 1995) Instructor (Mathematics) MIT (1992 – 1994) Computer Scientist NASA Ames Research Center (Summer 1993) Research Scientist Xerox Palo Alto Research Center (1991 – 1992) EDUCATION: Ph.D. (Computer Science) Carnegie Mellon University (1991) Thesis: “A Unified Geometric Approach to Graph Partitioning.” Advisor: Gary Lee Miller M.S. (Computer Science) University of Southern California (1988) Thesis: “Security, Verifiablity, and Universality in Distributed Computing”. Advised by Leonard Adleman and Ming-Deh Huang B.S. (Computer Science) & B.A. (Electrical -

Analysis and Modeling of Advanced PIM Architecture Design Tradeoffs
Analysis and Modeling of Advanced PIM Architecture Design Tradeoffs∗ Ed Upchurch Thomas Sterling California Institute of Technology Jay Brockman University of Notre Dame October 6, 2004 1 Introduction A major trend in high performance computer architecture over the last two decades is the mi- gration of memory in the form of high speed caches onto the microprocessor semiconductor die. Where temporal locality in the computation is high, caches prove very effective at hiding memory access latency and contention for communication resources. However where temporal locality is absent, caches may exhibit low hit rates resulting in poor operational efficiency. Vector computing exploiting pipelined arithmetic units and memory access address this challenge for certain forms of data access patterns, for example involving long contiguous data sets exhibiting high spatial locality. But for many advanced applications for science, technology, and national security at least some data access patterns are not consistent to the restricted forms well handled by either caches or vector processing. An important alternative is the reverse strategy; that of migrating logic in to the main memory (DRAM) and performing those operations directly on the data stored there. Processor in Memory (PIM) architecture has advanced to the point where it may fill this role and provide an important new mechanism for improving performance and efficiency of future super- computers for a broad range of applications. One important project considering both the role of PIM in supercomputer architecture and the design of such PIM components is the Cray Cascade Project sponsored by the DARPA High Productivity Computing Program. Cascade is a Petaflops scale computer targeted for deployment at the end of the decade that merges the raw speed of an advanced custom vector architecture with the high memory bandwidth processing delivered by an innovative class of PIM architecture. -

Lori L. Pollock September 2008 Personal Data Research Interests
Vita Lori L. Pollock September 2008 Personal Data Address: Dept. of Computer and Information Sciences University of Delaware Newark, DE 19716 Phone: 302 831-1953 Email: [email protected] Research Interests Program analysis, software testing, software maintenance tools, compiler optimization for parallel architectures. Education Ph.D. Computer Science, April 1986, University of Pittsburgh, Pittsburgh, PA Dissertation: An approach to incremental compilation of optimized code Advisor: Mary Lou Soffa M.S. Computer Science, August 1983, University of Pittsburgh B.S. Computer Science, magna cum laude, June 1981, Allegheny College, Meadville, PA B.S. Economics, magna cum laude, June 1981, Allegheny College, Meadville, PA Professional Experience September 2004 to present: Professor, Department of Computer and Information Sciences, University of Delaware. September 1998 to 2003: Associate Professor, Department of Computer and Information Sciences, University of Delaware. September 1998 to May 1999: Research Consultant, Army Research Laboratory, Aberdeen, MD. September 1992 to September 1998: Assistant Professor, Department of Computer and Information Sciences, University of Delaware. June-August, 1993 and 1994: Research Scientist, Supercomputing Research Center, Bowie, MD. September 1991 to August 1992: Visiting Assistant Professor, Department of Computer and Information Sciences, University of Delaware. January 1986 to May 1990: Assistant Professor, Department of Computer Science, Rice University. September 1982 to September 1984: Teaching assistant and Instructor, Department of Computer Science, University of Pittsburgh. 1 June-August 1982: Programmer, Hagerstown Cash Register, Inc., Hagerstown, MD. Journal Publications and Book Chapters Zachary P. Fry, David Shepherd, Emily Hill, Lori Pollock, K. Vijay-Shanker, “Analyzing Source Code: Looking for Useful Verb-Direct Object Pairs in All the Right Places,” IET Software Special Issue on Natural Language in Software Development, Vol. -

Brittany Terese Fasy
Brittany Terese Fasy Contact Department of Computer Science Phone: 1.919.346.3279 Information Tulane University E-mail: [email protected] New Orleans, Louisiana 70118 Web: www.fasy.us Education Ph.D., Computer Science, 2012 Duke University, Durham, NC Thesis: Modes of Gaussian Mixtures and an Inequality for the Distance Between Curves in Space Adviser: Herbert Edelsbrunner B.S., Mathematics and Computer Science, 2007 Saint Joseph's University, Philadelphia, PA Honors Program. Summa Cum Laude. Thesis: Homotopy Classification of the Components of the Space of Maps into an Aspherical Space: a Problem in the Intersection of Group Theory and Topology Adviser: Samuel Smith Faculty Assistant Professor, Computer Science, starting Fall 2015 Position Montana State University, Bozeman, MT Research Postdoctoral Fellow, Computer Science, 2013 { present Positions Tulane University, New Orleans, LA Adviser: Carola Wenk Postdoctoral Fellow, Computer Science, 2012 { 2013 Carnegie Mellon University, Pittsburgh, PA Visiting Scientist, 2009 { 2012 IST Austria, Vienna, Austria College Student Senior Technical Specialist, May 2006 { August 2008 Lockheed Martin, King of Prussia, PA Lockheed Martin, Gaithersburg, MD University Scholar Research, Mathematics, 2006 { 2007 Saint Joseph's University, Philadelphia, PA Adviser: Samuel Smith. Summer Research Scholar, Computer Science Education, 2004 { 2005 Saint Joseph's University, Philadelphia, PA Adviser: Steve Cooper. Teaching Co-Instructor, Computational Geometry (Undergraduate), January 2013 - May 2013 Experience -

ACM SIGACT Announces 2017 Awards Gödel, Knuth and Distinguished Service Prizes Recognize Contributions to Algorithms and Compu
Contact: Michael Mitzenmacher Jim Ormond ACM SIGACT Chair ACM 617-496-7172 212-626-0505 [email protected] [email protected] ACM SIGACT Announces 2017 Awards Gödel, Knuth and Distinguished Service Prizes Recognize Contributions to Algorithms and Computation Theory Community NEW YORK, June 19, 2017 – The Association for Computing Machinery’s Special Interest Group on Algorithms and Computation Theory (SIGACT) recently announced the recipients of three significant awards. The 2017 Gödel Prize is awarded to Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith for their work on differential privacy in their paper “Calibrating Noise to Sensitivity in Private Data Analysis.” The 2017 Donald E. Knuth Prize is awarded to Oded Goldreich of the Weizmann Institute of Science for fundamental and lasting contributions to many areas of theoretical computer science, including cryptography, probabilistically checkable proofs, inapproximability, property testing, and several other areas in complexity theory. Also this year, Alistair Sinclair of the University of California, Berkeley is the recipient of the 2017 ACM SIGACT Distinguished Service Prize for his role in the spectacular success of The Simons Institute for the Theory of Computing. These awards will be presented at the 49th Annual ACM Symposium on the Theory of Computing (STOC 2017), to be held June 19-23, in Montreal, Canada. 2017 Gödel Prize Differential privacy is a powerful theoretical model for dealing with the privacy of statistical data. The intellectual impact of differential privacy has been broad, influencing thinking about privacy across many disciplines. The work of Cynthia Dwork (Harvard University), Frank McSherry (independent researcher), Kobbi Nissim (Harvard University), and Adam Smith (Harvard University) launched a new line of theoretical research aimed at understanding the possibilities and limitations of differentially private algorithms. -

The Future of Scientific Workflows 1
5)&'6563& 0'4$*&/5*'*$ 803,'-084 2%0/24/&4(%$/%.'.3#33#)%.4)&)#7/2+&,/737/2+3(/0 !02),n 3PONSOREDBYTHE/FFICEOF!DVANCED3CIENTIFIC#OMPUTING2ESEARCH 53$EPARTMENTOF%NERGY /FFICEOF3CIENCE The Future of Scientific Workflows 1 Cover images courtesy of LSC LIGO Scientific Collaboration, www.ligo.org 2 The Future of Scientific Workflows Th The Future of Scientific Workflows Report of the DOE NGNS/CS Scientific Workflows Workshop Rockville, Maryland April 20-21, 2015 Meeting Organizers Ewa Deelman (USC) (co-organizer) Kenneth Moreland (SNL) Tom Peterka (ANL) (co-organizer) Manish Parashar (RU) Ilkay Altintas (SDSC) Lavanya Ramakrishnan (LBNL) Christopher Carothers (RPI) Michela Taufer (UD) Kerstin Kleese van Dam (PNNL) Jeffrey Vetter (ORNL) Meeting Participants Greg Abram (UT) Scott Klasky (ORNL) Gagan Agrawal (OSU) Jim Kowalkowski (FNAL) Jim Ahrens (LANL) Dan Laney (LLNL) Pavan Balaji (ANL) Miron Livny (UW) Ilya Baldin (RENCI) Allen Malony (UO) Jim Belak (LLNL) Anirban Mandal (RENCI) Amber Boehnlein (SLAC) Folker Meyer (ANL) Shreyas Cholia (NERSC) Dave Montoya (LANL) Alok Choudhary (NU) Peter Nugent (LBNL) Constantinos Evangelinos (IBM) Valerio Pascucci (UU) Ian Foster (ANL) Wilfred Pinfold (Intel) Geoffrey Fox (IU) Thomas Proffen (ORNL) Foss Friedman-Hill (SNL) Rob Ross (ANL) Jonathan Gallmeier (AMD) Erich Strohmaier (LBNL) Al Geist (ORNL) Christine Sweeney (LANL) Berk Geveci (Kitware) Douglas Thain (UND) Gary Grider (LANL) Craig Tull (LBNL) Mary Hall (UU) Tom Uram (ANL) Ming Jiang (LLNL) Dean Williams (LLNL) Elizabeth Jurrus (UU) Matt Wolf (GT) Gideon Juve (USC) John Wright (MIT) Larry Kaplan (Cray) John Wu (LBNL) Dimitri Katramatos (BNL) Frank Wuerthwein (UCSD) Dan Katz (UC) Dantong Yu (BNL) Darren Kerbyson (PNNL) DOE Program Managers Richard Carlson Lucy Nowell The Future of Scientific Workflows 3 Table of Contents 1 Executive Summary .........................................................................