DOCSLIB.ORG

A Simplified Model of All-Sky Artificial Sky Glow Derived from VIIRS Day

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Simplified Model of All-Sky Artificial Sky Glow Derived from VIIRS Day Journal of Quantitative Spectroscopy & Radiative Transfer 214 (2018) 133–145 Contents lists available at ScienceDirect Journal of Quantitative Spectroscopy & Radiative Transfer journal homepage: www.elsevier.com/locate/jqsrt A simplified model of all-sky artificial sky glow derived from VIIRS Day/Night band data ∗ Dan M. Duriscoe a, Sharolyn J. Anderson b, , Christian B. Luginbuhl c, Kimberly E. Baugh d a U.S. National Park Service Night Skies Program (retired), Big Pine, CA, USA b National Park Service, Natural Sounds and Night Skies, Fort Collins, CO, USA c Dark Sky Partners LLC, Tucson, AZ, USA d University of Colorado- CIRES, Boulder, CO, USA a r t i c l e i n f o a b s t r a c t Article history: We present a simplified method using geographic analysis tools to predict the average artificial luminance Received 15 November 2017 over the hemisphere of the night sky, expressed as a ratio to the natural condition. The VIIRS Day/Night Revised 25 April 2018 Band upward radiance data from the Suomi NPP orbiting satellite was used for input to the model. The Accepted 25 April 2018 method is based upon a relation between sky glow brightness and the distance from the observer to the Available online 26 April 2018 source of upward radiance. This relationship was developed using a Garstang radiative transfer model Keywords: with Day/Night Band data as input, then refined and calibrated with ground-based all-sky V-band photo- Night sky brightness metric data taken under cloudless and low atmospheric aerosol conditions. An excellent correlation was Light pollution found between observed sky quality and the predicted values from the remotely sensed data. Thematic Landscape scale assessments maps of large regions of the earth showing predicted artificial V-band sky brightness may be quickly gen- erated with modest computing resources. We have found a fast and accurate method based on previous work to model all-sky quality. We provide limitations to this method. The proposed model meets require- ments needed by decision makers and land managers of an easy to interpret and understand metric of sky quality. Published by Elsevier Ltd. This is an open access article under the CC BY license. ( http://creativecommons.org/licenses/by/4.0/ ) 1. Introduction and previous work velopment of this tool to advance conservation of scenic resources and the quality of visitor experience. Sky glow from escaped anthropogenic light degrades visual night sky quality. Sky glow results from reflection and scattering of stray light by molecules and aerosols in the atmosphere. Mea- 1.1. Measurements of artificial sky glow surements and models of this phenomenon are useful in evaluat- ing the effect of sky glow on the visual nightscape. This paper de- Astronomical observations of background night sky brightness velops a method to predict sky glow luminance using Geographic from large observatory telescopes provide one measure of night Information System (GIS) analysis applied to readily available re- sky quality. These observations are nearly always of an area near motely sensed upward radiance measures. The result, distance- the zenith or the darkest part of the night sky, e.g. [1,2] . Zenith weighted neighborhood sums of upward radiance around each ob- sky brightness has also been measured by citizen science projects servation point, have been calibrated with contemporaneous sky and researchers using low cost devices such as the Unihedron SQM brightness measurements of artificial sky glow. The model works and SQM-L. [3–5] . Zenith sky brightness, or zenith luminance (ZL), best in protected areas distant from major cities and other artificial is important to astronomical observations and is an informative in- light sources. It provides an accessible tool to evaluate the amount dicator of sky quality in moderate to severely light polluted areas. of sky glow and the quality of the night sky on large landscape The U.S. National Park Service (NPS) and natural resource managers scales. The U. S. National Park Service has participated in the de- characterize the condition of the entire night sky using average sky luminance (or ASL) [7] . This is a more sensitive measure of sky glow because light domes are more intense near the horizon than near the zenith. It is a more relevant measure of sky quality be- ∗ Corresponding author. cause wildlife and park visitors are more likely to have the horizon E-mail address: [email protected] (S.J. Anderson). in view than the zenith. https://doi.org/10.1016/j.jqsrt.2018.04.028 0022-4073/Published by Elsevier Ltd. This is an open access article under the CC BY license. ( http://creativecommons.org/licenses/by/4.0/ ) 134 D.M. Duriscoe et al. / Journal of Quantitative Spectroscopy & Radiative Transfer 214 (2018) 133–145 Accurate measurements of artificial sky glow in areas distant Berry [11] , and translated into a computer model by Pike [12] in from the sources, may only be obtained when the natural light the 1970 s. These models utilized human population as a surrogate from the night sky is removed from luminance observations, since for the amount of escaped outdoor light produced by a city. They the observed sky brightness is the combination of artificial and also included the distance from the observer to the city and a mea- natural sources. For this reason the NPS developed a method of sure of the aerosol content of the air as input parameters. In the pixel-by-pixel subtraction of a natural sky model from photomet- late 1970 s, Walker [13] developed a brightness/distance relation- rically calibrated all sky image mosaics [6] . A similar method has ship from a source of fixed escaped light from observations of sky been used to improve zenith brightness measures with the SQM-L brightness at progressively greater distances from the same city. A [7] . Values of 171 μcd m −2 and 250 μcd m −2 have been proposed simple function where the distance is raised to power −2.5 was as the reference conditions for ZL and ASL, respectively, in the ab- found to fit the data, the relationship is known as "Walker’s Law." sence of artificial sky glow [8] . These values provide a baseline This relationship was expanded by Albers and Duriscoe [14] who level for expressing the scale of sky glow. For many audiences, the derived a constant to convert from population to predicted artifi- condition of the night sky is more expressively rendered in terms cial sky brightness for cities. Netzel and Netzel [15] used high res- of a unitless ratio to natural conditions. The ratio indicators uti- olution daytime satellite imagery classified as "percent of built up lized in this paper are termed all-sky average light pollution ratio area" as a surrogate for escaped artificial light and Berry’s empiri- (ALR) and zenith light pollution ratio (ZLR). Numeric indicators of cal model to produce an estimate of sky brightness at zenith over artificial sky brightness were discussed in detail by Duriscoe [8] , the country of Poland at 100 m resolution with modest computer including their derivation from all sky photometric measurements resources using GIS tools. The model was calibrated with observa- and application to night sky quality assessments. tional sky brightness data from 65 sites. These empirical models To summarize the important sky brightness measures used in paved the way to constructing landscape scale models of the sky this paper, for the hemisphere of sky with azimuth angle ϕ, zenith brightness at zenith. −2 angle z , and punctual luminance B ϕ,z in μcd m : zenith lumi- nance: 1.2.2. Physical models A complex physical model of atmospheric scattering of light ZL = B ϕ, (1) 0 from ground based sources was described by Garstang [16–18] . The anthropogenic zenith luminance: model predicts the punctual sky brightness as seen by an observer on earth at any given point in the sky from any number of sources. Z L = Z L − Z L (2) a n Garstang’s radiative transfer model was adapted to produce the where ZL n = natural sky background brightness at zenith, reference first World Atlas of Artificial Night Sky Brightness in 2001 by Cin- condition set to 171 μcd m −2 zenith light pollution ratio: zano et al. [19] . Covering most of the land area of earth and using upward radiance data derived from DMSP-OLS satellite imagery as ZLR = Z L / 171 (3) a input [20] , the atlas is the pioneering landscape-scale assessment average sky luminance: of night sky quality based upon a physical model. The New World π/ π Atlas of Artificial Night Sky Brightness [7] utilized VIIRS Day/Night 2 2 1 ASL = B ϕ,z sin ( z )d ϕ d z (4) band upward radiance data [21] from 2014. The atlas used an en- π 2 0 0 hanced version of the Garstang model [22] was calibrated to thou- anthropogenic average sky luminance: sands of ground based observations over a several year period. π/ π Both atlases expressed artificial sky brightness as a ratio to a natu- 2 2 1 2 2 AS L a = ( B − B n )ϕ , sin ( z )d ϕ d z (5) ral background condition set at 251 μcd/m and 174 μcd/m in the π z 2 0 0 "first" and "new" editions, respectively. Both required substantial where B n = natural sky background brightness at φ, z computational resources and the assumption of a constant concen- With the reference condition for the all-sky average set to 250 tration of aerosols over the entire earth. μcd m −2 , all-sky light pollution ratio: Physical models have been used to refine the Walker’s Law neg- ative exponential zenith brightness/distance relationship.
Load more

Recommended publications
  • GLOBE at Night: Using Sky Quality Meters to Measure Sky Brightness
    GLOBE at Night: using Sky Quality Meters to measure sky brightness This document includes: • How to observe with the SQM o The SQM, finding latitude and longitude, when to observe, taking and reporting measurements, what do the numbers mean, comparing results • Demonstrating light pollution o Background in light pollution and lighting, materials needed for the shielding demo, doing the shielding demo • Capstone activities (and resources) • Appendix: An excel file for multiple measurements CREDITS This document on citizen-scientists using Sky Quality Meters to monitor light pollution levels in their community was a collaborative effort between Connie Walker at the National Optical Astronomy Observatory, Chuck Bueter of nightwise.org, Anna Hurst of ASP’s Astronomy from the Ground Up program, Vivian White and Marni Berendsen of ASP’s Night Sky Network and Kim Patten of the International Dark-Sky Association. Observations using the Sky Quality Meter (SQM) The Sky Quality Meters (SQMs) add a new twist to the GLOBE at Night program. They expand the citizen science experience by making it more scientific and more precise. The SQMs allow citizen-scientists to map a city at different locations to identify dark sky oases and even measure changes over time beyond the GLOBE at Night campaign. This document outlines how to make and report SQM observations. Important parts of the SQM ! Push start button here. ! Light enters here. ! Read out numbers here. The SQM Model The SQM-L Model Using the SQM There are two models of Sky Quality Meters. Information on the newer model, the SQM- L, can be found along with the instruction sheet at http://unihedron.com/projects/sqm-l/.
    [Show full text]
  • The Dawn Sky Brightness Observations in the Preliminary Shubuh Prayer Time Determination
    QIJIS: Qudus International Journal of Islamic Studies Volume 6, Issue 1, February 2018 THE DAWN SKY BRIGHTNESS OBSERVATIONS IN THE PRELIMINARY SHUBUH PRAYER TIME DETERMINATION Laksmiyanti Annake Harijadi Noor Bandung Institute of Technology (ITB) Bandung, West Java [email protected] Fahmi Fatwa Rosyadi Satria Hamdani Bandung Islamic University (UNISBA) Bandung, West Java [email protected] Abstract The indication of began to enter the shubuh prayer time is when emerge the morning dawn and lasted until the sun rises. The sun position when emerge the morning dawn is below the intrinsic horizon marked with a minus sign (-) with the value of a certain height. The Ministry of Religious Affairs has set the sun altitudes of dawn in the shubuh prayer time with minus (-) 19° + sunrise/sunset altitudes as standard is the reference time of dawn prayers in Indonesia. However, this provision in fact reap discourse in some quarters because it is not in accordance with the phenomenon of morning dawn emergence at the beginning of the shubuh prayer time empirically. This study aims to decide the morning dawn, as the beginning of dawn determinant. The tool used in this study is the Sky Quality Meter (SQM), to detecting the morning dawn emergence as a sign of the beginning of the shubuh prayer time. The results of this study found that the brightness of the sky throughout Fahmi Fatwa Rosyadi Satria Hamdani the night or the morning dawn in Tayu Beach, Pati, Central Java, in the span of four days of observation that is at 04.31 A.M. with an average altitude of the sun is -17°(17° below the horizon).
    [Show full text]
  • Daytime Sky Brightness Characterization for Persistent GEO SSA
    Daytime sky brightness characterization for persistent GEO SSA Grant M. Thomas Air Force Institute of Technology, Wright-Patterson AFB, Ohio Richard G. Cobb Air Force Institute of Technology, Wright-Patterson AFB, Ohio ABSTRACT Space Situational Awareness (SSA) is fundamental to operating in space. SSA for collision avoidance ensures safety of flight for both government and commercial spacecraft through persistent monitoring. A worldwide network of optical and radar sensors gather satellite ephemeris data from the nighttime sky. Current practice for daytime satellite tracking is limited exclusively to radar as the brightening daytime sky prevents the use of visible-band optical sensors. Radar coverage is not pervasive and results in significant daytime coverage gaps in SSA. To mitigate these gaps, optical telescopes equipped with sensors in the near-infrared band (0.75-0.9µm) may be used. The diminished intensity of the background sky radiance in the near-infrared band may allow for daylight tracking further into the twilight hours. To determine the performance of a near-infrared sensor for daylight custody, the sky background radiance must first be characterized spectrally as a function of wavelength. Using a physics-based atmospheric model with access to near-real time weather, we developed a generalized model for the apparent sky brightness of the Geostationary satellite belt. The model results are then compared to measured data collected from Dayton, OH through various look and Sun angles for model validation and spectral sky radiance quantification in the visible and near-infrared bands. 1 INTRODUCTION Spectral sky radiance or spectral sky brightness is a measure of the radiant intensity at each wavelength of the atmosphere.
    [Show full text]
  • Measuring Night Sky Brightness: Methods and Challenges
    Measuring night sky brightness: methods and challenges Andreas H¨anel1, Thomas Posch2, Salvador J. Ribas3,4, Martin Aub´e5, Dan Duriscoe6, Andreas Jechow7,13, Zolt´anKollath8, Dorien E. Lolkema9, Chadwick Moore6, Norbert Schmidt10, Henk Spoelstra11, G¨unther Wuchterl12, and Christopher C. M. Kyba13,7 1Planetarium Osnabr¨uck,Klaus-Strick-Weg 10, D-49082 Osnabr¨uck,Germany 2Universit¨atWien, Institut f¨urAstrophysik, T¨urkenschanzstraße 17, 1180 Wien, Austria tel: +43 1 4277 53800, e-mail: [email protected] (corresponding author) 3Parc Astron`omicMontsec, Comarcal de la Noguera, Pg. Angel Guimer`a28-30, 25600 Balaguer, Lleida, Spain 4Institut de Ci`encies del Cosmos (ICCUB), Universitat de Barcelona, C.Mart´ıi Franqu´es 1, 08028 Barcelona, Spain 5D´epartement de physique, C´egep de Sherbrooke, Sherbrooke, Qu´ebec, J1E 4K1, Canada 6Formerly with US National Park Service, Natural Sounds & Night Skies Division, 1201 Oakridge Dr, Suite 100, Fort Collins, CO 80525, USA 7Leibniz-Institute of Freshwater Ecology and Inland Fisheries, 12587 Berlin, Germany 8E¨otv¨osLor´andUniversity, Savaria Department of Physics, K´arolyi G´asp´ar t´er4, 9700 Szombathely, Hungary 9National Institute for Public Health and the Environment, 3720 Bilthoven, The Netherlands 10DDQ Apps, Webservices, Project Management, Maastricht, The Netherlands 11LightPollutionMonitoring.Net, Urb. Ve¨ınatVerneda 101 (Bustia 49), 17244 Cass`ade la Selva, Girona, Spain 12Kuffner-Sternwarte,Johann-Staud-Straße 10, A-1160 Wien, Austria 13Deutsches GeoForschungsZentrum Potsdam, Telegrafenberg, 14473 Potsdam, Germany Abstract Measuring the brightness of the night sky has become an increasingly impor- tant topic in recent years, as artificial lights and their scattering by the Earth’s atmosphere continue spreading around the globe.
    [Show full text]
  • Measurements of Night Sky Brightness in the Veneto Region of Italy: Sky Quality Meter Network Results and Differential Photometry by Digital Single Lens Reflex
    Journal of Imaging Article Measurements of Night Sky Brightness in the Veneto Region of Italy: Sky Quality Meter Network Results and Differential Photometry by Digital Single Lens Reflex Andrea Bertolo 1,* , Renata Binotto 1, Sergio Ortolani 2,3 and Simone Sapienza 1 1 Regional Environmental Protection Agency of Veneto, Via Ospedale Civile 24, 35121 Padova, Italy; [email protected] (R.B.); [email protected] (S.S.) 2 Department of Physics and Astronomy, University of Padova, vicolo dell’Osservatorio 2, 35122 Padova, Italy; [email protected] 3 INAF, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy * Correspondence: [email protected] Received: 3 April 2019; Accepted: 21 May 2019; Published: 24 May 2019 Abstract: In this paper, we present the implementation of a monitoring network for artificial light at night (ALAN), based on Sky Quality Meter devices (SQM) installed in seven locations of the Veneto region. The system is coordinated by the Regional Environmental Protection Agency (ARPA-Veneto) and the Department of Physics and Astronomy of the University of Padova, in collaboration with a local dark-sky association, Venetostellato. A new centralized database containing zenith night sky brightness (NSB) data was implemented to collect data from all SQM stations of the regional territory, not only in real time (since 2017), but in some stations since 2011. We now have a dataset to determine how light pollution is affecting astronomical observatories. A WEB portal was created to offer different downloads from these NSB data. We present the results of some elaborations for the 2018 dataset (statistics, histograms, annual and cumulative plots) for seven monitoring sites.
    [Show full text]
  • The 1997 Reference of Diffuse Night Sky Brightness
    ASTRONOMY & ASTROPHYSICS JANUARY I 1998,PAGE1 SUPPLEMENT SERIES Astron. Astrophys. Suppl. Ser. 127, 1-99 (1998) The 1997 reference of diffuse night sky brightness? Ch. Leinert1,S.Bowyer2, L.K. Haikala3, M.S. Hanner4,M.G.Hauser5, A.-Ch. Levasseur-Regourd6, I. Mann7,K.Mattila3, W.T. Reach8, W. Schlosser9, H.J. Staude1, G.N. Toller10, J.L. Weiland11, J.L. Weinberg12, and A.N. Witt13 1 Max–Planck–Institut f¨ur Astronomie, K¨onigstuhl 17, D-69117 Heidelberg, Germany 2 Astronomy Dept., University of California, 601 Campbell Hall, Berkeley CA 94720, U.S.A. 3 Observatory, P.O. Box 14, FIN-00014 University of Helsinki, Finland 4 Jet Propulsion Laboratory, 4800 Oak Grove Drive, Pasadena CA 91109, U.S.A. 5 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218, U.S.A. 6 Service d’A´eronomie, BP. 3, F-91371 Verri`eres le Buisson, France 7 Max–Planck–Institut f¨ur Aeronomie, Max-Planck-Straße 2, D-37191 Katlenburg-Lindau, Germany 8 Institut d’Astrophysique Spatiale, Universit´e Paris XI, 91405 Orsay Cedex, France 9 Astronomisches Institut, Ruhr-Universit¨at Bochum, D-44780 Bochum, Germany 10 General Sciences Corporation, 6100 Chevy Chase Drive, Laurel, MD 20707, U.S.A. 11 Hughes STX, NASA/Goddard Space Flight Center Code 685.9, Greenbelt, MD 20771, U.S.A. 12 MK Industries, 2137E Flintstone Drive, Tucker, Georgia 30084, U.S.A. 13 Ritter Astrophys. Res. Center, University of Toledo, Toledo, OH 43606, U.S.A. Received August 7; accepted September 8, 1997 Abstract. In the following we present material in tabu- 6.4 Geocorona lar and graphical form, with the aim to allow the non- 6.5 Interplanetary emissions specialist to obtain a realistic estimate of the diffuse night 6.6 Shuttle glow sky brightness over a wide range of wavelengths from the 7.
    [Show full text]
  • Lab 2: Sky Brightness
    Lab 2: Sky Brightness As we discussed in class, the brightness of the night sky during an observation depends upon a number of factors. These factors include the wavelength of the observations, airmass, cloud-cover, the location and phase of the moon, and terrestrial light pollution. In this lab your objective is to directly investigate the sky brightness at Rosemary Hill Observatory using a sky quality meter during our RHO trip. As always, the lab report that you turn in should provide clear explanations of your work, and include the requested numbers, figures, and tables. Objectives: Your basic objectives for the lab are the following. 1. Quantify the dependence of sky brightness upon time after sunset. 2. Quantify the dependence of sky brightness upon zenith angle. 3. Compare the minimum sky brightness at Rosemary Hill Observatory with numbers for at least one other research observatory at a dark site (be sure to cite your reference for these numbers). Your report should include a table with the darkest sky levels at each site. 4. Discuss and attempt to explain any anomalous data. Procedure: During the trip to RHO, we will have on hand a sky quality meter. The unit is point-and- shoot, providing the sky brightness in visual magnitudes per square arcsec. The Full Width Half Maximum (FWHM) of the angular sensitivity is 20 degrees, so if you for example point at zenith the meter is sensitive to the sky brightness within ~10 degrees. We will share the meter as a class. All measurements should be made from a single location.
    [Show full text]
  • Measuring Night-Sky Brightness with a Wide-Field CCD Camera
    Publications of the Astronomical Society of the Pacific ᭧ Measuring Night-Sky Brightness with a Wide-Field CCD Camera Dan M. Duriscoe Death Valley National Park, Death Valley, CA; [email protected] Christian B. Luginbuhl US Naval Observatory Flagstaff Station, Flagstaff, AZ; [email protected] and Chadwick A. Moore Bryce Canyon National Park, Bryce Canyon, UT; [email protected] Received 2006 November 13; accepted 2006 December 26; published 2007 February 13 ABSTRACT. We describe a system for rapidly measuring the brightness of the night sky using a mosaic of CCD images obtained with a low-cost automated system. The portable system produces millions of independent photometric measurements covering the entire sky, enabling the detailed characterization of natural sky conditions and light domes produced by cities. The measurements are calibrated using images of standard stars contained within the raw data, producing results closely tracking the Johnson V astronomical standard. The National Park Service has collected hundreds of data sets at numerous parks since 2001 and is using these data for the protection and monitoring of the night-sky visual resource. This system also allows comprehensive characterization of sky conditions at astronomical observatories. We explore photometric issues raised by the broadband measurement of the complex and variable night-sky spectrum, and potential indices of night-sky quality. 1. INTRODUCTION (such as the TASCA camera at Cerro Tololo Inter-American Observatory [Schwarz et al. 2003] and the network of contin- The National Park Service’s mission of preservation of na- uous night-sky cameras known as CONCAM [Pereira & Nem- tional park resources and values requires accurate information iroff 1998]), but such images are difficult to calibrate to known on past, present, and future conditions.
    [Show full text]
  • Introducing the Bortle Dark-Sky Scale
    observer’s log Introducing the Bortle Dark-Sky Scale Excellent? Typical? Urban? Use this nine-step scale to rate the sky conditions at any observing site. By John E. Bortle ow dark is your sky? A Limiting Magnitude Isn’t Enough precise answer to this ques- Amateur astronomers usually judge their tion is useful for comparing skies by noting the magnitude of the observing sites and, more im- faintest star visible to the naked eye. Hportant, for determining whether a site is However, naked-eye limiting magnitude dark enough to let you push your eyes, is a poor criterion. It depends too much telescope, or camera to their theoretical on a person’s visual acuity (sharpness of limits. Likewise, you need accurate crite- eyesight), as well as on the time and ef- ria for judging sky conditions when doc- fort expended to see the faintest possible umenting unusual or borderline obser- stars. One person’s “5.5-magnitude sky” vations, such as an extremely long comet is another’s “6.3-magnitude sky.” More- tail, a faint aurora, or subtle features in over, deep-sky observers need to assess the galaxies. visibility of both stellar and nonstellar ob- On Internet bulletin boards and news- jects. A modest amount of light pollution groups I see many postings from begin- degrades diffuse objects such as comets, ners (and sometimes more experienced nebulae, and galaxies far more than stars. observers) wondering how to evaluate To help observers judge the true dark- the quality of their skies. Unfortunately, ness of a site, I have created a nine-level most of today’s stargazers have never scale.
    [Show full text]
  • Open Access Proceedings Journal of Physics: Conference Series
    International Journal of Science and Applied Science: Conference Series P-ISSN: 2549-4635 Int. J. Sci. Appl. Sci.: Conf. Ser., Vol. 2 No. 1 (2017) E-ISSN: 2549-4627 International Conference on Science and Applied Science 2017 http://jurnal.uns.ac.id/ijsascs The moon phases influence on the beginning of astronomical dawn determination in Yogyakarta Abu Yazid Raisal1, Yudhiakto Pramudya1,2, Okimustava2 and Muchlas1,2 1 Program Studi Magister Pendidikan Fisika Universitas Ahmad Dahlan, Jalan Pramuka 42, Sidikan, Umbulharjo, Yogyakarta 55161 2 Pusat Studi Astronomi Universitas Ahmad Dahlan, Jalan Gondosuli 1 Yogyakarta [email protected] Abstract: In astronomy, there are three types of dawn. They are astronomical, nautical, and civil dawn. The sunlight is starting to appear on the east horizon when the Sun altitude is 18o below the horizon. Hence, there is a change on the sky brightness. The sky brightness can be affected by the moon phases. The sky brightness level is monitored by Sky Quality Meter (SQM). The SQM was installed upward to the zenith. There are 4 locations of measurement in Yogyakarta. The data has been collected for nine months to obtain the complete moon phases. The beginning of astronomical dawn is time when the sky brightness level is starting to decrease. The moving average algorithm was employed to determine the beginning of astronomical dawn. The time when the astronomical dawn begins is compared with the sun altitude calculation. The sun altitude calculation has been done using accurate times software. The difference of the beginning of astronomical dawn by measurement and calculation are 18.61±6.81 minutes, 19.12±3.28 minutes, 31.12±7.76 minutes, and 27.24±8.04 minutes, on the new moon (0), on the first quarter (0.25), on the full moon (0.5) and on the last quarter (0.75), respectively.
    [Show full text]
  • The Proliferation of Space Objects Is a Rapidly Increasing Source of Artificial
    MNRAS 000,1{6 (2015) Preprint 24 March 2021 Compiled using MNRAS LATEX style file v3.0 The proliferation of space objects is a rapidly increasing source of artificial night sky brightness M. Kocifaj,1;2? F. Kundracik,2 J. C. Barentine,3;4 S. Bar´a,5 1ICA, Slovak Academy of Sciences, D´ubravsk´acesta 9, 845 03 Bratislava, Slovakia 2Department of Experimental Physics, FMPI, Comenius University, Mlynsk´adolina, 842 48 Bratislava, Slovakia 3International Dark-Sky Association, 3223 N. 1st Ave, Tucson, AZ 85710 USA 4Consortium for Dark Sky Studies, University of Utah, 375 S 1530 E, RM 235 ARCH, Salt Lake City, Utah 84112-0730 USA 5Departamento de F´ısica Aplicada, Universidade de Santiago de Compostela, E-15782 Santiago de Compostela, Galicia, Spain Accepted XXX. Received YYY; in original form ZZZ ABSTRACT The population of artificial satellites and space debris orbiting the Earth imposes non-negligible constraints on both space operations and ground-based optical and ra- dio astronomy. The ongoing deployment of several satellite `mega-constellations' in the 2020s represents an additional threat that raises significant concerns. The expected severity of its unwanted consequences is still under study, including radio interference and information loss by satellite streaks appearing in science images. In this Letter, we report a new skyglow effect produced by space objects: increased night sky bright- ness caused by sunlight reflected and scattered by that large set of orbiting bodies whose direct radiance is a diffuse component when observed with the naked eye or with low angular resolution photometric instruments. According to our preliminary estimates, the zenith luminance of this additional light pollution source may have al- ready reached ∼20 µcd m−2, which amounts to an approximately 10 percent increase over the brightness of the night sky determined by natural sources of light.
    [Show full text]
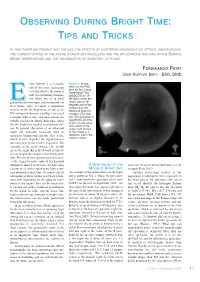
  • Observing During Bright Time: Tips and Tricks
    OOBSERBSERVINGVING DDURINGURING BBRIGHTRIGHT TTIMEIME:: TTIPSIPS ANDAND TTRICKSRICKS IN THIS PAPER WE PRESENT AND DISCUSS THE EFFECTS OF SCATTERED MOONLIGHT ON OPTICAL OBSERVATIONS, THE CURRENT STATUS OF THE MOONLIT NIGHT SKY MODELLING AND THE IMPLICATIONS THIS HAS ON THE SERVICE MODE OBSERVATIONS AND THE MAXIMISATION OF SCIENTIFIC OUTCOME. FERDINANDO PATAT USER SUPPORT DEPT. - ESO, DMD VEN THOUGH it is certainly Figure 1: Image one of the most fascinating taken by the ESO celestial objects, the moon is Mini All-Sky Cloud Observation Tool indeed a disturbing compan- (MASCOT) on 19- ion when one is to push 09-2004, when the Eground-based telescopes and instruments to moon was at 16 E degrees above the their limits, since it causes a significant horizon and the increase in the sky brightness, at least in the fractional lunar illu- UV and optical domains (see Fig. 1 for a real mination (FLI) was example). This is why such observations are 0.2. The greyscale is usually carried out during dark time, when logarithmic and the the sky brightness reaches its minimum val- bright circular struc- ture visible in the ues. In general, the effect of an enhanced upper right corner night sky emission translates into an of the image is a increased background photon shot noise, reflection within the which in turn, degrades the signal-to-noise camera optics. one can reach in the science exposures. For example, in the most extreme case of full moon, the night sky in the B-band is typical- ly four magnitudes brighter than during dark time. For any given exposure time, this caus- es the signal-to-noise ratio of background dominated images to decrease by more than A SPECTRUM OF THE value one measures during dark time (see for a factor of six with respect to the same expo- MOONLIT NIGHTIGHT SKY example Patat 2003).
    [Show full text]