Factor Models for Recommending Given Names
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Name Index to Photograph Collection
Name Index to Photograph Collection What follows is a name index only to the Finnish American Historical Archives' Historic Photograph Collection (Old Topical File). See Archival Finding Aids for a complete listing of this collection. When more than one surname was indicated concerning one photo, the entry with the first surname lists all of the individuals, while each additional surname is also listed individually. The metadata concerning each photograph is limited to whatever information is available on the object, often revealing limitations to the information about each object (for example, a mounted card photo that simply states "Mrs. Maki," or an group photo that only includes surnames). Another limitation is the legibility and clarity of the handwriting. This name index was created by Larissa Poyhonen in the summer of 2010, while performing preservation work on this collection. Megan Ott transcribed the Knights of Kaleva Convention Photograph in November, 2010. The index was edited and prepared for the Internet by Kent Randell. This index also includes the Knights of Kaleva Convention Photograph, August, 1910 The index also includes the pictures included in the book Tervehdys Suomelle, published in Brooklyn, N.Y. in 1920. Folder name Name Notes 002 Indvid – A- Aartila, Toivo Rudyard Am 062- Orgs.- Temperance- Aartilla, Toivo Marquette, Mich; 1917 Michigan Tervehdys Suomelle book Aatila, Julle p. 37 (1920) 021- Postcards- Finland- Imig. & Abbot, Mr & Mrs. Robert Collection Folkways 002 Indvid – A- Grand Marais, Mich., 50th Abramson, Axel and Helga Am Anniversary 1964, #12997 002 Indvid – A- Ahlman, Mrs; Hakola, Maria; Ahlman, Newberry, Mich. Am Pastor Lauri. Tervehdys Suomelle book Aho, Antti p. -

Ákos Lakatos University of Debrecen, Hungary Allan Hani State Real Estate Ltd, RKAS, Estonia Anatolijs Borodiņecs Riga Technic
Ákos Lakatos University of Debrecen, Hungary Allan Hani State Real Estate Ltd, RKAS, Estonia Anatolijs Borodiņecs Riga Technical University, Latvia Anders Kumlin Anders Kumlin AB, Sweden André Desjarlais Oak Ridge National Laboratory, Canada Andreas Nicolai Technical University of Dresden, Germany Andrius Jurelionis Kaunas University of Technology, Lithuania Angela Sasic Kalagasidis Chalmers University of Technology, Sweden Czech Technical University in Prague, Czech Antonín Lupíšek Republic Ardeshir Mahdavi Vienna University of Technology, Austria Norwegian University of Science and Arild Gustavsen Technology, NTNU, Norway Arnold Janssens Ghent University, Belgium Berit Time SINTEF, Norway Eindhoven University of Technology, The Bert Blocken Netherlands Birgit Risholt SINTEF, Norway Norwegian University of Science and Bjørn Petter Jelle Technology, NTNU, Norway Carl-Eric Hagentoft Chalmers University of Technology, Sweden Carsten Rode Technical Univ. of Denmark DTU, Denmark Daisuke Ogura Kyoto University, Japan Dariusz Gawin Technical University of Lodz, Lodz, Poland Dariusz Heim Technical University of Lodz, Poland Dirk Saelens KU Leuven, Belgium Swiss Federal Laboratories for Materials Science Dominique Derome and Technology, Empa, Switzerland Dušan Petráš Slovak University of Technology, Slovakia Endrik Arumägi Tallinn University of Technology, Estonia Enrico Fabrizio Politecnico di Torino, Italy Eva Sikander Research Institutes of Sweden, RISE, Sweden Canada Research Chair in Whole-Building Fitsum Tariku Performance, Canada Fraunhofer -

Ontanogon County Naturalization Index
Ontanogon County Naturalization Index Last Name First Name Middle Name First Paper Second Paper Aahaekarpi Anton V4,P158 Aalta John V12,P48 Aalto Fredrik Ivar V4,P282 Aalto John V4,P135 Aalto Sigrid V21,P699 Aarnio Eddie V5,P47 Abe Anton V5,P105 Abe Jacob V5,P273 Abfall Valentine V6,P404 Abraham George V3,P23 Abrahamson Henry V4,P149 Abramovich Frank V6,P238 Abramovich Johan V16,P79 V16,P79 Abramovich Stanko V9,P1131 Abramson Anna Moilanen B2,F1,P810 Adair Alpheus C. V11,P32 Adair Alpheus C. V3,P254 Adams Christopher V10,P143 Adams Christopher B1,F5,P4 B1,F5,P4 Adams Henry V4,P258 Aeshlinen Christ V3,P104 Agere Joseph V3,P89 Aguisti Adolo V6,P212 Ahala Alekx V6,P416 Thursday, August 05, 2004 Ontonagon County Page1 of 234 Last Name First Name Middle Name First Paper Second Paper Ahistus Jaako V16,P31 V16,P31 Ahlholm Karl August V22,P747 V22,P747 Ahlholm Vendla B2,F8,P987 Aho Aili Marie B2,F6,P930 Aho Antti V13,P68 Aho Antti V18,P4 V18,P4 Aho Antti V6,P51 Aho Charles Gust V17,P100 Aho Edward V5,P275 Aho Elias V6,P91 Aho Erik J. V4,P183 Aho Gust V5,P239 Aho Herman V6,P368 Aho Herman V19,P16 V19,P16 Aho Jacob V4,P69 Aho Jacob V13,P56 Aho Johan V5,P11 Aho John V6,P294 Aho John V13,P69 Aho Minnie Sanna B2,F7,P974 B2,F7,P974 Aho Minnie Sanna V9,P1050 Aho Nestori V15,P85 V15,P85 Aho Nistari V14,P53 Aho Oskar Jarvi V6,P74 Aho Viktori Ranto V6,P70 Ahola Alex V9,P1026 Thursday, August 05, 2004 Ontonagon County Page2 of 234 Last Name First Name Middle Name First Paper Second Paper Ahola Alexa B2,F2,P863 Ahola Matti V15,P38 V15,P38 Ahteenpaa Jaakka -
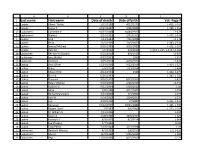
Last Name First Name Date of Death Date of Birth Vol.-Page
A B C D E 1 Last name First name Date of death Date of birth Vol.-Page # 2 Laajala Albert "Abbie" 1/12/1980 4/27/1933 L-421, L-535 3 Laajala Esther K 10/27/1997 2/28/1909 L-399, L-553 4 Laakaniemi Catherine V 10/21/2009 10/30/1922 L2-679 5 Laakaniemi Waino J 3/24/1992 2/22/1919 L-427, L-546 6 Laakko Emil 7/13/1983 7/11/1908 L2-178 7 Laakko Hilda 12/1/1969 11/5/1873 L-383, L-534 8 Laakko Samuel Michael 8/28/1980 8/28/1980 L-421, L-535 9 Laakko Vera M 7/6/2002 6/4/1912 L-214, L-215, L-232, L2-382 10 Laakkonen Bernice W (Stolpe) 5/23/2010 8/8/1925 L2-547 11 Laakkonen June (Kallio) 8/22/2003 1930 L-157 12 Laakonen Clarence 7/25/2014 4/26/1929 L2-474 13 Laakso Arvo Oliver 11/14/1998 9/22/1916 L-404, L-527 14 Laakso Bruce 5/6/2014 7/23/1934 L2-494 15 Laakso Edward Erik 4/24/1994 1944 L-342, L-479 16 Laakso Elvira E 6/30/1997 L-387, L-531 17 Laakso Florence 9/10/1977 8/15/1919 L-421 18 Laakso Helen Mildred 9/10/2006 2/26/1923 L2-432 19 Laakso Herbert G 6/12/2004 5/30/1917 L-85 20 Laakso Hilda 7/8/1988 4/17/1907 L-254 21 Laakso Hilma (Manninen) 4/17/2000 7/4/1900 L-273 22 Laakso Jack W 5/24/2002 2/14/1937 L-233 23 Laakso Joel 4/28/1958 2//1887 L-421, L-535 24 Laakso Kustaava 10/12/1955 10/21/1882 L-421, L-535 25 Laakso Rupert "Sam" 7//1987 5/6/1905 L-222, L-254 26 Laakso Tri William A 4/11/1995 L-328 27 Laakso Roger A 2/28/2008 10/8/1935 L-624 28 Laakso Rudolph A 6/9/1905 8/7/1914 L-648 29 Laakso Eva (Tissary) 1/7/1996 L2-84 30 Laakso Toini Perko 7/19/2004 3/12/1918 L-49 31 Laaksonen Bertha H (Nisula) 4/1/2005 1/6/1917 L-2, L-619 32 Laaksonen -

Club Name Last Name First Name Age Group Division Total 0Tri1 Triathlon Team Como 1 Papagallo Andrea M30-34 V 1. FC Kaiserslaute
Club Name Last Name First Name Age Group Division Total 0Tri1 Triathlon Team Como 1 Papagallo Andrea M30-34 V 1. FC Kaiserslautern Triathlon 1 Becker Arno M50-54 V 1. Triathlon Club Oldenburg Die Bären 1 Berdjis Navid M50-54 V 2tri 1 Badensø Kenneth M40-44 V 3bike.ch | Team 1 Denyes Jenna F30-34 IV 3City Triathlon 2 Wendelius Ludvig M30-34 IV Adolfsson Peter M50-54 IV 3D Fitness Race Team 1 Mcgirl Louise F45-49 V 3D Triathlon Vietnam 1 Nguyen Tuan M40-44 V 3K Sport 1 Komac Marko M45-49 IV 3MD 6 De Beul Bart M50-54 IV Claus Dieter M35-39 IV D'Haese Kevin M35-39 IV De Smet Laurens M30-34 IV De Rybel Ruud M25-29 IV Van Langenhove Simon M25-29 IV 21CC Triatloniklubi 2 Hääl Indrek M40-44 IV Rosen Ulf M50-54 IV 338 Småland Triathlon & Multisport 1 Bergqvist Mikael M55-59 IV /tri club denmark 63 Karlsson Alexander M25-29 II Bussek-Sedzinski Alexandra F35-39 II Eriksen Allan M40-44 II Eriksen Anders Wøhlk M35-39 II Fernandes Quilelli Andres Eduardo M25-29 II Blicher Anette F60-64 II Christiansen Anna-Marie F30-34 II Klærke-Olesen Anne Leth F30-34 II Poulsen Bjarne M55-59 II Skovgaard Pedersen Camilla F40-44 II Thorsen Christian Munch M50-54 II Petersen Claus M55-59 II Rindshoej Claus M50-54 II Larsen Claus Wiegand M55-59 II Hammarbro Ligaard Daniel M40-44 II Maman David M40-44 II Christensen Dennis M40-44 II Hansen Dorthe F35-39 II Olsen Frank M55-59 II Bruun Axelsen Henrik M45-49 II Larsen Henrik M50-54 II Rudolf Henrik M45-49 II Francke Christensen Jacob M35-39 II Olsen Jacob M30-34 II Thomsen Jakob M40-44 II Reichl Jan M50-54 II Gerlach Jan-Peter -

First Name: Initiation Year Patsy Kjosness Gottschalk 1946
First Name: Initiation Year Patsy Kjosness Gottschalk 1946 Rosermary Harland Pennell 1947 jackie mitchell last 1948 Jody Getty Norman 1948 Becky Barline Boyington 1948 Carm McMahon Johnson 1948 Sheila Janssen Klages 1950 Ernestine Gohrband Oringdulph 1951 Mary Carnoll Heath 1951 Mary Lou Varian Porter 1951 Margery Nobles McIntosh 1951 Gwen Tupper Soderberg 1951 Joann Smith Lefferts 1951 Pat Long Odberg 1951 Carolyn Gale Louthian 1952 Jo Harwood Flynn 1952 June Powels Smith 1953 Janet Austad Parks 1953 June Powels Smith 1953 Marilyn Norseth Will 1954 Carolyn Sanderson Staley 1954 Rosemarie Perrin Bowman 1954 Judy Crookham Krueger 1954 Karen Crozier Smith 1955 Dorothy Bauer Schedler 1956 Rosemary Maule Daubert 1956 Marjie Bradbury Johnson 1956 Eleanor Whitney Fowler 1956 Suzanne Roffler Tarlov 1956 Pat Casey Nelson 1956 Ella Taye Springer Williams 1956 Barbara Tatum Snow 1957 Judy Orcutt Burke-Chelius 1957 Ann Irwin Shively 1958 Karen (Stedtfeld) Offen 1958 Patsy Rogers Mosman 1958 Kay Irwin Rowley 1959 Heather Hill Chrisman 1959 Linda Ensign Dashew 1959 Lynda Herndon Carey 1960 Kathryn Rodell Hunt 1960 Judy Powers Arnt 1960 Jo Ann Tatum Hattner 1960 Ann Rosendahl White 1960 Rowena Eikum Henry 1960 Linda Engle Sande 1960 Janice Rieman Gisler 1961 Mary Casey Ratcliffe 1961 Pat Swan Gustavel 1961 Jeanne Maxey Reese 1961 Alice Fulcher Anderson 1962 Bonnie Johansen Bruce 1962 Barbara Ware Featherstone 1962 Joan Sorensen Sullivan 1962 Judy Frazier Livingston 1962 Leslie Ensign Hall 1963 Nina Jenkins Bartlett 1963 Barbara Doll Keithly 1963 Zena -

Naughty and Nice List, 2020
North Pole Government NAUGHTY & NICE LIST 2020 NAUGHTY & NICE LIST Naughty and Nice List 2020 This is the Secretary’s This list relates to the people of the world’s performance for 2020 against the measures outlined Naughty and Nice in the Christmas Behaviour Statements. list to the Minister for Christmas Affairs In addition to providing an alphabetised list of all naughty and nice people for the year 2020, this for the financial year document contains details of how to rectify a ended 30 June 2020. naughty reputation. 2 | © Copyright North Pole Government 2020 christmasaffairs.com North Pole Government, Department of Christmas Affairs | Naughty and Nice List, 2020 Contents About this list 04 Official list (in alphabetical order) 05 Disputes 173 Rehabilitation 174 3 | © Copyright North Pole Government 2020 christmasaffairs.com North Pole Government, Department of Christmas Affairs | Naughty and Nice List, 2018-192020 About this list This list relates to the people of the world’s performance for 2020 against the measures outlined in the Christmas Behaviour Statements. In addition to providing an alphabetised list of all naughty and nice people for the 2020 financial year, this document contains details of how to rectify a naughty reputation. 4 | © Copyright North Pole Government 2020 christmasaffairs.com North Pole Government, Department of Christmas Affairs | Naughty and Nice List, 2020 Official list in alphabetical order A.J. Nice Abbott Nice Aaden Nice Abby Nice Aalani Naughty Abbygail Nice Aalia Naughty Abbygale Nice Aalis Nice Abdiel -

Baby Boy Names Registered in 2017
Page 1 of 43 Baby Boy Names Registered in 2017 # Baby Boy Names # Baby Boy Names # Baby Boy Names 1 Aaban 3 Abbas 1 Abhigyan 1 Aadam 2 Abd 2 Abhijot 1 Aaden 1 Abdaleh 1 Abhinav 1 Aadhith 3 Abdalla 1 Abhir 2 Aadi 4 Abdallah 1 Abhiraj 2 Aadil 1 Abd-AlMoez 1 Abic 1 Aadish 1 Abd-Alrahman 1 Abin 2 Aaditya 1 Abdelatif 1 Abir 2 Aadvik 1 Abdelaziz 11 Abraham 1 Aafiq 1 Abdelmonem 7 Abram 1 Aaftaab 1 Abdelrhman 1 Abrham 1 Aagam 1 Abdi 1 Abrielle 2 Aahil 1 Abdihafid 1 Absaar 1 Aaman 2 Abdikarim 1 Absalom 1 Aamir 1 Abdikhabir 1 Abu 1 Aanav 1 Abdilahi 1 Abubacarr 24 Aarav 1 Abdinasir 1 Abubakar 1 Aaravjot 1 Abdi-Raheem 2 Abubakr 1 Aarez 7 Abdirahman 2 Abu-Bakr 1 Aaric 1 Abdirisaq 1 Abubeker 1 Aarish 2 Abdirizak 1 Abuoi 1 Aarit 1 Abdisamad 1 Abyan 1 Aariv 1 Abdishakur 13 Ace 1 Aariyan 1 Abdiziz 1 Achier 2 Aariz 2 Abdoul 4 Achilles 2 Aarnav 2 Abdoulaye 1 Achyut 1 Aaro 1 Abdourahman 1 Adab 68 Aaron 10 Abdul 1 Adabjot 1 Aaron-Clive 1 Abdulahad 1 Adalius 2 Aarsh 1 Abdul-Azeem 133 Adam 1 Aarudh 1 Abdulaziz 2 Adama 1 Aarus 1 Abdulbasit 1 Adamas 4 Aarush 1 Abdulla 1 Adarius 1 Aarvsh 19 Abdullah 1 Adden 9 Aaryan 5 Abdullahi 4 Addison 1 Aaryansh 1 Abdulmuhsin 1 Adedayo 1 Aaryav 1 Abdul-Muqsit 1 Adeel 1 Aaryn 1 Abdulrahim 1 Adeen 1 Aashir 2 Abdulrahman 1 Adeendra 1 Aashish 1 Abdul-Rahman 1 Adekayode 2 Aasim 1 Abdulsattar 4 Adel 1 Aaven 2 Abdur 1 Ademidesireoluwa 1 Aavish 1 Abdur-Rahman 1 Ademidun 3 Aayan 1 Abe 5 Aden 1 Aayandeep 1 Abed 1 A'den 1 Aayansh 21 Abel 1 Adeoluwa 1 Abaan 1 Abenzer 1 Adetola 1 Abanoub 1 Abhaypratap 1 Adetunde 1 Abantsia 1 Abheytej 3 -

Conference & Workshop Program
8TH INTERNATIONAL CONFERENCE & WORKSHOP “MEDICAL PHYSICS 2010” 14 - 16 October 2010, Kaunas, Lithuania CONFERENCE & WORKSHOP PROGRAM Thursday, 14 October 2010 13.30-14.00 Registration of participants at Kaunas Medical University Hospital branch Oncology Hospital Volungių str. 16, Kaunas Session 1. Chair: Jurgita Laurikaitienė 14.00-14.15 Welcome to the Oncology Hospital: Artūras Andrejaitis, Vice-Director; Dr. Marius Laurikaitis, Medical physicist 14.15-14.45 Tommy Knöös. Lessons learned from accidents in radiation therapy: how to prevent them? 14.45-15.00 A. Miller, L. Kasulaitytė. IMRT for craniospinal irradiation: challenges and results 15.00-15.15 E. Jakubovskij, R. Griškevičius, A. Miller. IMRT commissioning: Baltic institutions planning and dosimetry comparisons 15.15-15.30 Fredrik Nordström, Sacha AF Wettersted, Sven ÅJ Bäck. Quality assurance methods in radiotherapy 15.30-15.45 R. Vilkas, M. Laurikaitis, D. Adlienė, V. Andrijaitienė. Implementation of the patient plan checking in radiotherapy 15.45-16.00 Coffee break Session2. Chair: Dr. Marius Laurikaitis QUALITY ASSURANCE SEMINAR 16.00-16.15 Miglė Šniurevičiūtė. Quality assurance in brachytherapy 16.15-16.30 Romas Griškevičius. Quality assurance of modern radiotherapy procedures 16.30-16.45 Marius Laurikaitis. Quality assurance of distance radiotherapy 16.45-17.00 Tim Thurn (LAP GmbH Laser Applikationen). Virtual simulation and patient positioning in the field of radiotherapy 17.00-17.45 Visit to the Radiotherapy department 18.00-19.00 ANNUAL MEETING OF LITHUANIAN MEDICAL PHYSICISTS SOCIETY 1 Friday, 15 October 2010 9.00-9.30 Registration of participants at Kaunas University of Technology, Studentų str. 50–325F, Kaunas 9.15-9.30 Conference opening: Vytautas Janilionis, Dean of the Faculty of Fundamental Sciences; prof. -

HOME STATE HOME CITY HOME POSTAL First Name Middle Last
HOME STATE HOME CITY HOME POSTAL First Name Middle Last Major 1 Descrip Jonathan Robert Fisher Mathematics Major Hei Yeung Fung Finance Major Altenstadt 63674 Jaclyn Caroline Morgan International Exchange Bang Khae 10160 Arisra Lertrungarun International Exchange Busan Jaehyun An Management Major Copenhagen 2200 Marianne Jensby Larsen International Exchange DAEGU 701110 Hangi Park International Exchange Dong Ha Huong Thi Mai Vo Finance Major Frankfurt 60311 Nadine Ritz International Exchange Frankfurt 60389 Eugenia Canisius Udoumeobi International Exchange Frederiksberg 2000 Kalle Ohrt Stenbaek International Exchange Gaozhou 525200 Jingyu Liang English Major: Rhetoric and Writing Emphasis GRANADA 18008 Miguel Angel Hernandez Ianez International Exchange Guangzhou 510000 Yi Huang English Major: Rhetoric and Writing Emphasis Guangzhou 510000 Zeyao Wu English Major: Rhetoric and Writing Emphasis Ha Noi Huyen Ngoc Pham Management Major Hanoi Khanh Ngoc Nguyen Accountancy Major Hanoi Phuc Duc Pham Computer Science Major Hanoi Yen Hai Trinh Finance Major Hechi 547000 Yi Wei English Major: Rhetoric and Writing Emphasis Hvidovre 2650 Morten Guldbrandtsen Gilder International Exchange Kremsmuenster 4550 Gabriel Zwicklhuber International Exchange Mauá 09331040 Mariane Helen de Oliveira Undergraduate Special - Non Degree Nanning 530001 Jintian Li English Major: Rhetoric and Writing Emphasis Nanning 530300 Aijing Song English Major: Rhetoric and Writing Emphasis Nanning 530021 Shaohua Wei Accountancy Major Oldenburg 26121 Monia Ilana Meyer International -

Permits Issued with Fees and Values City of Salinas Date Range Between 11/1/2019 and 11/30/2019
Permits Issued with Fees and Values City of Salinas Date Range Between 11/1/2019 and 11/30/2019 PERMIT NUMBER PERMIT TYPE ADDRESS VALUATION ISSUED DATE PERMIT SUBTYPE PARCEL NUMBER TOTAL FEES APPLIED DATE STATUS SUBDIVISION TOTAL PAID CITY19-0683 CITY 244 HAWTHORNE ST $0.00 11/4/2019 R-CITY REPORT 002613011000 $69.30 11/1/2019 FINALED AVELAR TRACT NO. 2 $69.30 Owner Name: O MAHONEY MICHAEL J & SHANNON B TRS Contractor Name: CITY19-0684 CITY 440 COMANCHE WY $0.00 11/4/2019 R-CITY REPORT 261412021000 $69.30 11/4/2019 FINALED CRESCENT PARK UNIT 5 $69.30 Owner Name: CAMERA JANET K Contractor Name: CITY19-0685 CITY 151 CHRISTENSEN AVE $0.00 11/4/2019 R-CITY REPORT 261266007000 $69.30 11/4/2019 FINALED NORTHPOINT II (aka CALIFORNIA $69.30 VILLAS),HARDEN RANCH PHASE 1 (aka CANTERBURY PARK ) Owner Name: CRUZ ALFREDO & TERESA Contractor Name: CITY19-0686 CITY 1791 CHEROKEE DR 3 $0.00 11/4/2019 R-CITY REPORT 261762027000 $69.30 11/4/2019 FINALED NORTHGATE VILLAGE $69.30 Owner Name: TINOCO MARIA ISALIA Contractor Name: CITY19-0687 CITY 1556 DURAN ST $0.00 11/4/2019 R-CITY REPORT 261613014000 $69.30 11/4/2019 FINALED NORTHGATE UNIT 2 $69.30 Owner Name: BROWN ELLIOTT D & VIRGINIA F TRS Contractor Name: CITY19-0688 CITY 762 ALVARADO DR $0.00 11/5/2019 R-CITY REPORT 261773004000 $69.30 11/5/2019 FINALED LAUREL WEST UNIT 3,LAUREL WEST $69.30 UNIT 4 Owner Name: CISNEROS GEORGE & SHARON TRS Contractor Name: CITY19-0689 CITY 301 MAPLE ST $0.00 11/5/2019 R-CITY REPORT 002382045000 $69.30 Printed: Wednesday, 04 December, 2019 1 of 37 Permits Issued with Fees and Values City of Salinas Date Range Between 11/1/2019 and 11/30/2019 11/5/2019 FINALED $69.30 Owner Name: KENYON COLIN & KENYON ALISSA Contractor Name: CITY19-0690 CITY 654 CALAVERAS DR $0.00 11/5/2019 R-CITY REPORT 261492017000 $69.30 11/5/2019 FINALED SANTA LUCIA VILLAGE ADDITION NO. -

Babies' First Forenames: Births Registered in Scotland in 2012
Babies' first forenames: births registered in Scotland in 2012 Information about the basis of the list can be found via the 'Babies' First Names' page on the National Records of Scotland website. Boys Girls Position Name Number of babies Position Name Number of babies 1 Jack 539 1 Sophie 619 2 Lewis 438 2 Emily 489 3 James 428 3 Ava 435 4 Riley 418 4 Olivia 428 5 Logan 392 5 Lucy 418 6 Daniel 384 6 Isla 413 7 Ethan 352 7= Jessica 402 8 Harry 331 7= Lily 402 9 Alexander 327 9 Amelia 335 10 Oliver 311 10 Mia 300 11 Max 306 11 Millie 295 12 Charlie 298 12 Chloe 286 13= Finlay 296 13 Ellie 282 13= Tyler 296 14 Eva 280 15 Aaron 295 15 Sophia 258 16 Adam 291 16 Freya 256 17 Mason 287 17 Grace 249 18 Alfie 284 18 Holly 248 19 Ryan 278 19 Emma 243 20= Liam 271 20 Hannah 225 20= Lucas 271 21 Ruby 204 22 Jamie 266 22 Erin 198 23 Thomas 265 23 Amy 195 24 Callum 259 24 Ella 193 25 Cameron 258 25 Leah 190 26 Dylan 252 26 Eilidh 188 27 Kyle 249 27 Katie 187 28 Harris 242 28 Charlotte 180 29= Matthew 240 29 Brooke 175 29= Noah 240 30= Evie 173 31 Rory 233 30= Layla 173 32= Connor 225 32 Kayla 172 32= Joshua 225 33 Anna 169 34 Nathan 219 34 Rebecca 156 35 Jacob 216 35 Poppy 154 36 Aiden 200 36 Orla 149 37 William 199 37 Summer 145 38 Archie 197 38 Hollie 144 39 Leo 191 39 Niamh 141 40 Andrew 189 40 Lexi 140 41 Jayden 186 41 Lacey 138 42 Luke 183 42 Molly 132 43 Rhys 158 43= Amber 131 44 Kai 157 43= Isabella 131 45 David 155 45 Skye 130 46 Cole 152 46 Maisie 129 47= Joseph 151 47 Zoe 119 47= Michael 151 48 Abbie 118 49 Samuel 145 49 Daisy 117 50 Leon 144