Estimated Age Effects in Baseball
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
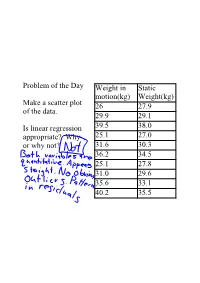
Problem of the Day Make a Scatter Plot of the Data. Is Linear Regression
Problem of the Day Weight in Static motion(kg) Weight(kg) Make a scatter plot 26 27.9 of the data. 29.9 29.1 Is linear regression 39.5 38.0 appropriate? Why 25.1 27.0 or why not? 31.6 30.3 36.2 34.5 25.1 27.8 31.0 29.6 35.6 33.1 40.2 35.5 Salary(in Problem of the Day Player Year millions) Nolan Ryan 1980 1.0 Is it appropriate to use George Foster 1982 2.0 linear regression Kirby Puckett 1990 3.0 to predict salary Jose Canseco 1991 4.7 from year? Roger Clemens 1996 5.3 Why or why not? Ken Griffey, Jr 1997 8.5 Albert Belle 1997 11.0 Pedro Martinez 1998 12.5 Mike Piazza 1999 12.5 Mo Vaughn 1999 13.3 Kevin Brown 1999 15.0 Carlos Delgado 2001 17.0 Alex Rodriguez 2001 22.0 Manny Ramirez 2004 22.5 Alex Rodriguez 2005 26.0 Chapter 10 ReExpressing Data: Get It Straight! Linear Regressioneasiest of methods, how can we make our data linear in appearance Can we reexpress data? Change functions or add a function? Can we think about data differently? What is the meaning of the yunits? Why do we need to reexpress? Methods to deal with data that we have learned 1. 2. Goal 1 making data symmetric Goal 2 make spreads more alike(centers are not necessarily alike), less spread out Goal 3(most used) make data appear more linear Goal 4(similar to Goal 3) make the data in a scatter plot more spread out Ladder of Powers(pg 227) Straightening is good, but limited multimodal data cannot be "straightened" multiple models is really the only way to deal with this data Things to Remember we want linear regression because it is easiest (curves are possible, but beyond the scope of our class) don't choose a model based on r or R2 don't go too far from the Ladder of Powers negative values or multimodal data are difficult to reexpress Salary(in Player Year Find an appropriate millions) Nolan Ryan 1980 1.0 linear model for the George Foster 1982 2.0 data. -
The Daily Scoreboard
10 – THE DERRICK. / The News-Herald Thursday, Aug. 14, 2014 THE DAILY SCOREBOARD Major League Baseball standings Pro golf glance Announcements Transactions LPGA TOUR BOWLING LEAGUES BASEBALL AMERICAN LEAGUE LPGA CHAMPIONSHIP Thursday Night Mixed League at Seneca Lanes is National League East Division Site: Pittsford, New York. set to meet on August 21 at 6:30 p.m. Everyone from CHICAGO CUBS — Sent LHP Felix Doubront to W L Pct GB WCGB L10 Str Home Away Schedule: Thursday-Sunday. the league is welcome to attend the meeting. After the Iowa (PCL) for a rehab assignment. Baltimore 69 50 .580 — — 8-2 W-2 34-26 35-24 Course: Monroe Golf Club (6,717 yards, par 72). meeting, it is open bowling for free. If y ou have any LOS ANGELES DODGERS — Released 3B Chone Toronto 63 58 .521 7 2½ 3-7 L-2 33-26 30-32 Purse: $2,225,000. Winner’s share: $337,000. questions, please contact Tina Exley, the league secre- Figgins. New York 61 58 .513 8 3½ 5-5 L-4 29-29 32-29 Television: Golf Channel (Thursday-Friday, 12:30-3 tary, or call Seneca Lanes. PITTSBURGH PIRATES — Claimed C Ramon p.m.; Saturday-Sunday, 3-7 p.m.) Tampa Bay 58 61 .487 11 6½ 5-5 L-1 27-32 31-29 Cabrera off waivers from Detroit. Designated RHP Last year: Inbee Park won the June event at Locust The fall meeting for the Let’s Take a Break League Wirfin Obispo for assignment. Boston 54 65 .454 15 10½ 5-5 W-3 27-31 27-34 will be held Wednesday, August 20 at 11 a.m. -

Vic Power Dies
University of Central Florida STARS On Sport and Society Public History 12-2-2005 Vic Power dies Richard C. Crepeau University of Central Florida, [email protected] Part of the Cultural History Commons, Journalism Studies Commons, Other History Commons, Sports Management Commons, and the Sports Studies Commons Find similar works at: https://stars.library.ucf.edu/onsportandsociety University of Central Florida Libraries http://library.ucf.edu This Commentary is brought to you for free and open access by the Public History at STARS. It has been accepted for inclusion in On Sport and Society by an authorized administrator of STARS. For more information, please contact [email protected]. Recommended Citation Crepeau, Richard C., "Vic Power dies" (2005). On Sport and Society. 676. https://stars.library.ucf.edu/onsportandsociety/676 SPORT AND SOCIETY FOR H-ARETE Vic Power dies DECEMBER 2, 2005 On Tuesday Victor Pellot died at age 78. This may not mean all that much to many baseball fans, but if that sentence is modified to read, "On Tuesday Vic Power died at age 78," it would have considerably more meaning. Vic Power was a first baseman who came to North America from Puerto Rico in 1950 to play baseball. He started in Class D ball in Ontario and a year later was signed by the Yankee organization. In 1952 he was assigned to the Yankee farm team in Kansas City where he hit .331 and drove in over a hundred runs. The next year he hit .349. He then was traded by the Yankees to the Philadelphia Athletics. -

Seattle Mariners Opening Day Record Book
SEATTLE MARINERS OPENING DAY RECORD BOOK 1977-2012 All-Time Openers Year Date Day Opponent Att. Time Score D/N 1977 4/6 Wed. CAL 57,762 2:40 L, 0-1 N 1978 4/5 Wed. MIN 45,235 2:15 W, 3-2 N 1979 4/4 Wed. CAL 37,748 2:23 W, 5-4 N 1980 4/9 Wed. TOR 22,588 2:34 W, 8-6 N 1981 4/9 Thurs. CAL 33,317 2:14 L, 2-6 N 1982 4/6 Tue. at MIN 52,279 2:32 W, 11-7 N 1983 4/5 Tue. NYY 37,015 2:53 W, 5-4 N 1984 4/4 Wed. TOR 43,200 2:50 W, 3-2 (10) N 1985 4/9 Tue. OAK 37,161 2:56 W, 6-3 N 1986 4/8 Tue. CAL 42,121 3:22 W, 8-4 (10) N 1987 4/7 Tue. at CAL 37,097 2:42 L, 1-7 D 1988 4/4 Mon. at OAK 45,333 2:24 L, 1-4 N 1989 4/3 Mon. at OAK 46,163 2:19 L, 2-3 N 1990 4/9 Mon. at CAL 38,406 2:56 W, 7-4 N 1991 4/9 Tue. CAL 53,671 2:40 L, 2-3 N 1992 4/6 Mon. TEX 55,918 3:52 L, 10-12 N 1993 4/6 Tue. TOR 56,120 2:41 W, 8-1 N 1994 4/4 Mon. at CLE 41,459 3:29 L, 3-4 (11) D 1995 4/27 Thurs. -

07-04-2012 Red Sox Ortiz 400 Home Run Sheet
399 CAREER HOME RUNS David Ortiz is 1 home run shy of becoming the 49th Major Leaguer to hit 400 home runs, the 21st left-handed batter to do it and the 20th player to reach 400 homers as an American Leaguer...Ortiz would be just the 8th active player to reach the mark. HR Date Opp. HR Date Opp. HR Date Opp. HR Date Opp. HR Date Opp. HR Date Opp. 1997 WITH MINNESOTA 63 7/3/2003 @TB 2005 WITH BOSTON 199 6/24/2006 PHI 2008 WITH BOSTON 334 6/29/2010 TBR 1 9/14/1997 @TEX 64 7/4/2003 @NYY 131 4/5/2005 @NYY 200 6/29/2006 NYM 267 4/2/2008 @OAK 335 7/11/2010 @TOR 65 7/4/2003 @NYY 201 7/1/2006 @FLA 1998 WITH MINNESOTA 132 4/9/2005 @TOR 268 4/18/2008 TEX 336 7/24/2010 @SEA 66 7/5/2003 @NYY 202 7/1/2006 @FLA 2 4/3/1998 KC 133 4/15/2005 TB 269 4/23/2008 LAA 337 7/26/2010 @LAA 67 7/5/2003 @NYY 203 7/2/2006 @FLA 3 4/13/1998 @TB 134 4/19/2005 TOR 270 4/24/2008 LAA 338 7/26/2010 @LAA 68 7/10/2003 @TOR 204 7/4/2006 @TB 4 4/18/1998 SEA 135 4/23/2005 @TB 271 4/30/2008 TOR 339 7/30/2010 DET 69 7/17/2003 TOR 205 7/6/2006 @TB 5 4/24/1998 @SEA 136 4/23/2005 @TB 272 5/5/2008 @DET 340 8/4/2010 CLE 70 7/31/2003 @TEX 206 7/6/2006 @TB 6 7/11/1998 @CLE 137 4/24/2005 @TB 273 5/6/2008 @DET 341 8/6/2010 @NYY 71 8/3/2003 @BAL 207 7/7/2006 @CHW 7 7/12/1998 @CLE 138 5/6/2005 SEA 274 5/17/2008-1 MIL 342 8/12/2010 @TOR 72 8/3/2003 @BAL 208 7/8/2006 @CHW 8 7/17/1998 @OAK 139 5/8/2005-2 SEA 275 5/18/2008 MIL 343 8/13/2010 @TEX 73 8/7/2003 ANA 209 7/15/2006 OAK 9 8/25/1998 @TB 140 5/15/2005 @SEA 276 5/18/2008 MIL 344 8/19/2010 LAA 74 8/7/2003 ANA 210 7/21/2006 @SEA 10 9/9/1998 -

Baseball Classics All-Time All-Star Greats Game Team Roster
BASEBALL CLASSICS® ALL-TIME ALL-STAR GREATS GAME TEAM ROSTER Baseball Classics has carefully analyzed and selected the top 400 Major League Baseball players voted to the All-Star team since it's inception in 1933. Incredibly, a total of 20 Cy Young or MVP winners were not voted to the All-Star team, but Baseball Classics included them in this amazing set for you to play. This rare collection of hand-selected superstars player cards are from the finest All-Star season to battle head-to-head across eras featuring 249 position players and 151 pitchers spanning 1933 to 2018! Enjoy endless hours of next generation MLB board game play managing these legendary ballplayers with color-coded player ratings based on years of time-tested algorithms to ensure they perform as they did in their careers. Enjoy Fast, Easy, & Statistically Accurate Baseball Classics next generation game play! Top 400 MLB All-Time All-Star Greats 1933 to present! Season/Team Player Season/Team Player Season/Team Player Season/Team Player 1933 Cincinnati Reds Chick Hafey 1942 St. Louis Cardinals Mort Cooper 1957 Milwaukee Braves Warren Spahn 1969 New York Mets Cleon Jones 1933 New York Giants Carl Hubbell 1942 St. Louis Cardinals Enos Slaughter 1957 Washington Senators Roy Sievers 1969 Oakland Athletics Reggie Jackson 1933 New York Yankees Babe Ruth 1943 New York Yankees Spud Chandler 1958 Boston Red Sox Jackie Jensen 1969 Pittsburgh Pirates Matty Alou 1933 New York Yankees Tony Lazzeri 1944 Boston Red Sox Bobby Doerr 1958 Chicago Cubs Ernie Banks 1969 San Francisco Giants Willie McCovey 1933 Philadelphia Athletics Jimmie Foxx 1944 St. -

MARINERS SINK ROSOX War on Narcotics Whose Funding Levels
Don't n^ss the annual Feast Fast this week... page 4 iManrljpalpr IpralJi Tuesday, Sept. 5, 1989 Newsstand Price: 35 Cents Bush maps iHaurltratrr Hrralfi NFL undergoing drug war radical changes tonight at 9 SPORTS see page 44 By Rita Beamish The Associated Press M ore U.S. military aid arrives in Colombia, page 9 WASHINGTON — President Bush, .issuing an anti-drug battle in one or two places. cry, tonight will urge a crack Bush's package for 1990 will be down on drug users and ask close to $2 billion above the Americans to join a $7.8 billion current anti-drug spending MARINERS SINK ROSOX war on narcotics whose funding levels. source he has yet to reveal. In his televised address, the For his first nationally tele president will dwell more on a vised address to the nation, general outline of his strategy AL Roundup scheduled for 9 p.m. EDT, Bush than on its cost specifics. The will talk about drugs in what White House planned to release White House Press Secretary those figures to the media today. BOSTON (AP) — Jeffrey Leonard broke a tie with Marlin Fitzwater called “ a per his career-high 22nd homer as the Seattle Mariners Bush will urge Americans “ to sonal message from himself to think about what drugs are doing played long ball to beat Bo.ston 7-2 Friday night, the American people that talks dropping the Red Sox four games out in the about the collective need of See WAR, page 10 American League East. society to pull together to solve Leonard broke a 2-2 tie against Mike Smithson in this problem.” the sixth and Dave Vallehithisseventh homer in the Bush will “ talk considerably seventh. -

2017 Information & Record Book
2017 INFORMATION & RECORD BOOK OWNERSHIP OF THE CLEVELAND INDIANS Paul J. Dolan John Sherman Owner/Chairman/Chief Executive Of¿ cer Vice Chairman The Dolan family's ownership of the Cleveland Indians enters its 18th season in 2017, while John Sherman was announced as Vice Chairman and minority ownership partner of the Paul Dolan begins his ¿ fth campaign as the primary control person of the franchise after Cleveland Indians on August 19, 2016. being formally approved by Major League Baseball on Jan. 10, 2013. Paul continues to A long-time entrepreneur and philanthropist, Sherman has been responsible for establishing serve as Chairman and Chief Executive Of¿ cer of the Indians, roles that he accepted prior two successful businesses in Kansas City, Missouri and has provided extensive charitable to the 2011 season. He began as Vice President, General Counsel of the Indians upon support throughout surrounding communities. joining the organization in 2000 and later served as the club's President from 2004-10. His ¿ rst startup, LPG Services Group, grew rapidly and merged with Dynegy (NYSE:DYN) Paul was born and raised in nearby Chardon, Ohio where he attended high school at in 1996. Sherman later founded Inergy L.P., which went public in 2001. He led Inergy Gilmour Academy in Gates Mills. He graduated with a B.A. degree from St. Lawrence through a period of tremendous growth, merging it with Crestwood Holdings in 2013, University in 1980 and received his Juris Doctorate from the University of Notre Dame’s and continues to serve on the board of [now] Crestwood Equity Partners (NYSE:CEQP). -
What Should the New Bob Hall Pier Look Like?
Inside the Moon Deep Sea Roundup A2 Pothole-a-palooza A6 Traveling Moon A9 Live Music A16 Photo by Natalie Werkhoven Issue 900 The 27° 37' 0.5952'' N | 97° 13' 21.4068'' W Island Free The voiceMoon of The Island since 1996 July 15, 2021 Weekly www.islandmoon.com FREE After this week it can rightfully be said that the Waves Waterpark is no more. All that is left now is to tear down the building. Photo by Dwight Jackson. By the numbers What Should the New Bob Rainfall Totals Hall Pier Look Like? on the Island The best thing one can do when it is raining is to let it rain. — By Dale Rankin Now is your chance to speak up Henry Wadsworth Longfellow It’s been a strange week here on our By Dale Rankin Location little sandbar. The enormous tourist Nueces County commissioners have crowds that have been swarming The signed a contract for the design of Jul 5 – 11 2021 year to date 2020 Island for months seemed to have the new Bob Hall Pier and are now year to date slowed a bit, maybe because of the reaching out to the public for input persistent rain, and the vehicle count Padre Island: Elbow St. 14.26” through a series of Virtual Town Hall 38.34” 13.81” coming OTB during the holiday meetings and an online survey. weekend just past was around 50,000 Padre Island: Scallop St. 13.23” per day which is significant but not Bob Hall (what was then called 38.50” 16.17” close to the 83,000 we saw in a single Nueces Beach Park) debuted the Padre Island: Cayo Cantiles St. -

Tonight's Game Information
Thursday, April 1, 2021 Game #1 (0-0) T-Mobile Park SEATTLE MARINERS (0-0) vs. SAN FRANCISCO GIANTS (0-0) Home #1 (0-0) TONIGHT’S GAME INFORMATION Starting Pitchers: LHP Marco Gonzales (7-2, 3.10 in ‘20) vs. RHP Kevin Gausman (3-3, 3.62 in ‘20) 7:10 pm PT • Radio: 710 ESPN / Mariners.com • TV: ROOT SPORTS NW Day Date Opp. Time (PT) Mariners Pitcher Opposing Pitcher RADIO Friday April 2 vs. SF 7:10 pm LH Yusei Kikuchi (6-9, 5.12 in ‘20) vs. RH Johnny Cueto (2-3, 5.40 in ‘20) 710 ESPN Saturday April 3 vs. SF 6:10 pm RH Chris Flexen (8-4, 3.01 in ‘20 KBO) vs. RH Logan Webb (3-4, 5.47 in ‘20) 710 ESPN Sunday April 4 OFF DAY TONIGHT’S TILT…the Mariners open their 45th season against the San Francisco Giants at T-Mobile INSIDE THE NUMBERS Park…tonight is the first of a 3-game series vs. the Giants…following Saturday’s game, the Mariners will enjoy an off day before hosting the White Sox for a 3-game set beginning on Monday, April 5…tonight’s game will be televised live on ROOT SPORTS NW and broadcast live on 710 ESPN Seattle and the 2 Mariners Radio Network. With a win in tonight’s game, Marco Gonzales would join Randy Johnson ODDS AND ENDS…the Mariners open the season against San Francisco for the first time in club history with 2 wins on Opening Day, trailing ...also marks the first time in club history the Mariners open with an interleague opponent...the Mariners are only Félix Hernández (7) for the most 12-4 over their last 16 Opening Day contests...are 3-1 at home during that span. -

Learning Unethical Practices from a Co-Worker: the Peer Effect of Jose Canseco
IZA DP No. 3328 Learning Unethical Practices from a Co-worker: The Peer Effect of Jose Canseco Eric D. Gould Todd R. Kaplan DISCUSSION PAPER SERIES DISCUSSION PAPER January 2008 Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of Labor Learning Unethical Practices from a Co-worker: The Peer Effect of Jose Canseco Eric D. Gould Hebrew University, Shalem Center, CEPR, CREAM and IZA Todd R. Kaplan Haifa University and University of Exeter Discussion Paper No. 3328 January 2008 IZA P.O. Box 7240 53072 Bonn Germany Phone: +49-228-3894-0 Fax: +49-228-3894-180 E-mail: [email protected] Any opinions expressed here are those of the author(s) and not those of IZA. Research published in this series may include views on policy, but the institute itself takes no institutional policy positions. The Institute for the Study of Labor (IZA) in Bonn is a local and virtual international research center and a place of communication between science, politics and business. IZA is an independent nonprofit organization supported by Deutsche Post World Net. The center is associated with the University of Bonn and offers a stimulating research environment through its international network, workshops and conferences, data service, project support, research visits and doctoral program. IZA engages in (i) original and internationally competitive research in all fields of labor economics, (ii) development of policy concepts, and (iii) dissemination of research results and concepts to the interested public. IZA Discussion Papers often represent preliminary work and are circulated to encourage discussion. Citation of such a paper should account for its provisional character. -

BOSTON RED SOX (0-0) Vs
WORLD SERIES CHAMPIONS (8): 1903, 1912, 1915, 1916, 1918, 2004, 2007, 2013 AMERICAN LEAGUE CHAMPIONS (13): 1903, 1904, 1912, 1915, 1916, 1918, 1946, 1967, 1975, 1986, 2004, 2007, 2013 AMERICAN LEAGUE EAST DIVISION CHAMPIONS (8): 1975, 1986, 1988, 1990, 1995, 2007, 2013, 2016 AMERICAN LEAGUE WILD CARD (7): 1998, 1999, 2003, 2004, 2005, 2008, 2009 @BOSTONREDSOXPR • HTTP://PRESSROOM.REDSOX.COM • @SOXNOTES BOSTON RED SOX (0-0) vs. PITTSBURGH PIRATES (0-0) Monday, April 3, 2017 • 2:05 p.m. ET • Fenway Park • Boston, MA RHP Rick Porcello (0-0, ---) vs. RHP Gerrit Cole (0-0, ---) Game #1 • Home Game #1 • TV: NESN • Radio: WEEI 93.7 FM, WCEC 1490 AM/103.7 FM (Spanish) FOR THE 117TH TIME: Boston begins its 117th AL season to- HAVE WE BENINTRODUCED?: Andrew Benintendi, who morrow vs. PIT...The Red Sox are 57-58-1 all-time on Opening will be 22 years and 271 days old tomorrow, could become 2016 SEASON BREAKDOWN Day (excluding G2 of doubleheaders in 1903, 1948, and 1982). the Red Sox’ youngest Opening Day starter in left field since AL East Standing .....................1st, +4.0 GA Home/Road ............................. 47-34/46-35 Carl Yastrzemski in 1962 (22 years, 231 days). Day/Night ................................ 27-23/66-46 STAYING HOME: This is the 41st time that the Red Sox April/May/June ..............14-10/18-10/10-16 have opened the regular season at home, snapping a streak KEYSTONE CONSISTENCY: Dustin Pedroia and Xander July/August ............................. 15-10/17-13 of 6 consecutive years opening on the road...Including this Bogaerts have been the Red Sox’ Opening Day starters at September/October ......................