DOCSLIB.ORG

Destination Dwarf Planets: a Panel Discussion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Destination Dwarf Planets: a Panel Discussion Destination Dwarf Planets: A Panel Discussion OPAG, August 2019 Convened: Orkan Umurhan (SETI/NASA-ARC) Co-Panelists: Walt Harris (LPL, UA) Kathleen Mandt (JHUAPL) Alan Stern (SWRI) Dwarf Planets/KBO: a rogues gallery Triton Unifying Story for these bodies awaits Perihelio n/ Diamet Aphelion DocumentGoals 09.2018) from OPAG (Taken Name Surface characteristics Other observations/ hypotheses Moons er (km) /Current Distance (AU) Eris ~2326 P=38 Appears almost white, albedo of 0.96, higher Largest KBO by mass second Dysnomia A=98 than any other large Solar System body except by size. Models of internal C=96 Enceledus. Methane ice appears to be quite radioactive decay indicate evenly spread over the surface that a subsurface water ocean may be stable Haumea ~1600 P=35 Displays a white surface with an albedo of 0.6- Is a triaxial ellipsoid, with its Hi’iaka and A=51 0.8 , and a large, dark red area . Surface shows major axis twice as long as Namaka C=51 the presence of crystalline water ice (66%-80%) , the minor. Rapid rotation (~4 but no methane, and may have undergone hrs), high density, and high resurfacing in the last 10 Myr. Hydrogen cyanide, albedo may be the result of a phyllosilicate clays, and inorganic cyanide salts giant collision. Has the only may be present , but organics are no more than ring system known for a TNO. 8% 2007 OR10 ~1535 P=33 Amongst the reddest objects known, perhaps due May retain a thin methane S/(225088) A=101 to the abundant presence of methane frosts atmosphere 1 C=87 (tholins?) across the surface.Surface also show the presence of water ice. P=39 Methane, ethane, tholins, and possibly nitrogen May have an atmosphere up MK 2 A=53 present on the surface. Smaller amounts of to 4-12 nanobar at surface. ethylene, acetylene, and high-mass alkanes (like May have N convecting Makemake ~1427 C=52 2 propane) may be present. Appears red in the layer. visible spectrum. Some nitrogen present, but much less than on Pluto or Triton. Perihelio n/ Diamet Aphelion DocumentGoals 09.2018) from OPAG (Taken Name Surface characteristics Other observations/ hypotheses Moons er (km) /Current Distance (AU) ~1092 P=42 Surface is moderately red, and albedo may Crystalline water ice indicates that Weywot Quaoar A=45 be as low as 0.1, maybe indicating that temperature rose to at least -110°K C=42 fresh ice has disappeared from its surface. sometime in the last 10 Ma, Crystalline water ice exists at the surface. possible cryovolcanism spurred by Small presence (5%) of methane and internal radioactive decay ethane ice Sedna ~1030 P=76 Has an albedo of 0.32, a homogeneous One of the most distant- known None A=936 surface in color and spectrum, and one of objects in the Solar System, with a detected C=86 the reddest surfaces in the Solar System, highly eccentric orbit, leading to perhaps caused by a surface coating of speculation that it may be a tholins. Surface composition upper limits member of the inner Oort cloud, in are 60% for methane and 70% for water ice. addition to extra- solar origin 24% Triton-type tholins, 7% amorphous hypotheses. Models of internal carbon, 10% nitrogen, 26% methanol, and radioactive decay indicate that a 33% methane have been suggested for the subsurface ocean may be stable. surface composition. Orcus 917 P=31 Has an albedo of 0.3, is gray in color, and is A plutino in a 2:3 resonance with Vanth A=48 rich in crystalline water ice, mixed with Neptune. Crystalline water ice, and C=48 tholins . Methane and ammonia may be possible ammonia ice, may present. Water and methane ices can cover indicate surface renewal by no more than 50% and 30% of the surface cryovolcanism. Models of internal respectively.,. radioactive decay indicate that a subsurface ocean may be stable. V&V Crosscutting Science Themes and Priority Questions, and candidate missions relevant to OPAG Crosscutting Candidate future missions Science Priority Questions to outer planets Themes 1. What were the initial stages, conditions, and processes of solar system formation and the Ice Giants mission, KBO nature of incorporated interstellar matter? mission, Saturn Probe 2. How did the giant planets and their satellite Ice Giants mission, Saturn systems accrete, and is there evidence that they Probe, Io Observer, multiple New Worlds migrated to new orbital positions? Ocean Worlds missions (ORIGINS) 3. What governed the accretion, supply of water, Ice Giants mission, KBO chemistry, and internal differentiation of the inner mission, Io Observer, Titan Building planets and the evolution of their atmospheres, mission (see Section 8.0) and what roles did bombardment by large Planetary habitats projectiles play? V&V Crosscutting Science Themes and Priority Questions, and candidate missions relevant to OPAG Crosscutting Candidate future missions Science Priority Questions to outer planets Themes 4. What were the primordial sources of organic Ice Giants mission, multiple matter, and where does organic synthesis Ocean Worlds missions, KBO continue today? mission 5. Did Mars or Venus host ancient aqueous environments conducive to early life, and is there N/A evidence that life emerged? 6. Beyond Earth, are there contemporary habitats elsewhere in the solar system with necessary Multiple Ocean Worlds Planetary Habitats conditions, organic matter, water, energy, and missions, Ice Giants mission nutrients to sustain life, and do organisms live there now? V&V Crosscutting Science Themes and Priority Questions, and candidate missions relevant to OPAG Crosscutting Candidate future missions Science Priority Questions to outer planets Themes 7. How do the giant planets serve as laboratories Ice Giants mission, Saturn to understand Earth, the solar system, and probe, multiple Ocean Worlds extrasolar planetary systems? missions, Io Observer 8. What solar system bodies endanger Earth’s N/A biosphere, and what mechanisms shield it? 9. Can understanding the roles of physics, Ice Giants mission, Saturn chemistry, geology, and dynamics in driving Probe, Titan mission, Io SYSTEM planetary atmospheres and climates lead to a Observer, KBO mission better understanding of climate change on Earth? 10. How have the myriad chemical and physical WORKINGS OF SOLAR WORKINGS OF processes that shaped the solar system operated, All missions interacted, and evolved over time? On the Value of a Pluto-Charon System Orbiter O.M. Umurhan with prime assistance from: Jason Hofgartner1, Bonnie Buratti1, Marc Buie2, Veronica Bray3, Emmanuel Lellouch4 1. Jet Propulsion Laboratory, California Institute of Technology; 2. Southwest Research Institute; 3. University of Arizona; 4. Observatoire de Paris, Meudon; © 2019 OPAG. Government sponsorship acknowledged. Pre-Decisional Information - For Planning and Discussion Purposes Only On the Value of a Pluto-Charon System Orbiter O.M. Umurhan with prime assistance from: Jason Hofgartner1, Bonnie Buratti1, Marc Buie2, Veronica Bray3, Emmanuel Lellouch4 “…because it has a little bit of all the KBO Dwarf Planets, that’s why” 1. Jet Propulsion Laboratory, California Institute of Technology; 2. Southwest Research Institute; 3. University of Arizona; 4. Observatoire de Paris, Meudon; © OPAG. Government sponsorship acknowledged. Pre-Decisional Information - For Planning and Discussion Purposes Only Diverse, Unique, Ongoing, Endogenic and Exogenic , Liquids?, Stratigraphy: Crust? Glaciers and volatile caps? Pluto Geology Polar night unknown, non-encounter side needs resolution. Global Map, most desirable. Instruments: Color cameras (narrow and wide angle), Altimeter, IR spectral imager, Polar night imaging: Radar, Laser, Lyman-α imager? Priority Science Question(s) Addressed 10. How have the myriad chemical and physical processes that shaped the solar system operated, interacted, and evolved over Cryovolcanism Glaciers time? Convection Sublimation Interior: Ocean? (likely) If so depth, thickness, composition? Sputnik Planitia: Mascon and Polar wander? Basin origin & age? Depth? Southern Sputnik? Tidal evolution. Pluto Geophysics Answers to most of these questions needs an orbiter Sputnik Planitia Instruments: Gravity, Magnetometry, Sounding Radar, Thermal IR/Sub-mm Priority Science Question(s) Addressed 1. What were the initial stages, conditions, and processes of solar system formation and the nature of incorporated interstellar matter ? 6. Beyond Earth, are there contemporary habitats elsewhere in the solar system with necessary conditions, organic matter, water, energy, and nutrients to sustain life, and do organisms live there now? 9. Can understanding the roles of physics, chemistry, geology, and dynamics in driving planetary atmospheres and climates lead to a better understanding of climate change on Earth? Spencer et al., 2019 10. How have the myriad chemical and physical processes that shaped the solar system operated, interacted, and evolved over time? Hazes: Origin? Composition & structure? Properties of Pluto Atmosphere Atmospheric Gravity/Wave Propagation? Layering? Cthulhu? Climate: Seasonal Changes? Extremes? and Climate Escape: Why is the exosphere so cold? Answers to most of these questions needs an orbiter as most of these processes vary on the timescales of days-weeks to decades!!! Instruments: mass spec, sub-mm, UV spectroscopy/occultations, radio occultations, color cameras, plasma spectrometer and waves The atmosphere and surface are intimately linked! Therefore Surface Appearance and Climate in tight dance Priority Science Question(s) Addressed 4. What were the primordial sources of organic matter, and where does organic synthesis
Load more

Recommended publications
  • Demoting Pluto Presentation
    WWhhaatt HHaappppeenneedd ttoo PPlluuttoo??!!!! Scale in the Solar System, New Discoveries, and the Nature of Science Mary L. Urquhart, Ph.D. Department of Science/Mathematics Education Marc Hairston, Ph.D. William B. Hanson Center for Space Sciences FFrroomm NNiinnee ttoo EEiigghhtt?? On August 24th Pluto was reclassified by the International Astronomical Union (IAU) as a “dwarf planet”. So what happens to “My Very Educated Mother Just Served Us Nine Pizzas”? OOffifficciiaall IAIAUU DDeefifinniittiioonn A planet: (a) is in orbit around the Sun, (b) has sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and (c) has cleared the neighborhood around its orbit. A dwarf planet must satisfy only the first two criteria. WWhhaatt iiss SScciieennccee?? National Science Education Standards (National Research Council, 1996) “…science reflects its history and is an ongoing, changing enterprise.” BBeeyyoonndd MMnneemmoonniiccss Science is “ not a collection of facts but an ongoing process, with continual revisions and refinements of concepts necessary in order to arrive at the best current views of the Universe.” - American Astronomical Society AA BBiitt ooff HHiiststoorryy • How have planets been historically defined? • Has a planet ever been demoted before? Planet (from Greek “planetes” meaning wanderer) This was the first definition of “planet” planet Latin English Spanish Italian French Sun Solis Sunday domingo domenica dimanche Moon Lunae Monday lunes lunedì lundi Mars Martis
    [Show full text]
  • Surface Characteristics of Transneptunian Objects and Centaurs from Photometry and Spectroscopy
    Barucci et al.: Surface Characteristics of TNOs and Centaurs 647 Surface Characteristics of Transneptunian Objects and Centaurs from Photometry and Spectroscopy M. A. Barucci and A. Doressoundiram Observatoire de Paris D. P. Cruikshank NASA Ames Research Center The external region of the solar system contains a vast population of small icy bodies, be- lieved to be remnants from the accretion of the planets. The transneptunian objects (TNOs) and Centaurs (located between Jupiter and Neptune) are probably made of the most primitive and thermally unprocessed materials of the known solar system. Although the study of these objects has rapidly evolved in the past few years, especially from dynamical and theoretical points of view, studies of the physical and chemical properties of the TNO population are still limited by the faintness of these objects. The basic properties of these objects, including infor- mation on their dimensions and rotation periods, are presented, with emphasis on their diver- sity and the possible characteristics of their surfaces. 1. INTRODUCTION cally with even the largest telescopes. The physical char- acteristics of Centaurs and TNOs are still in a rather early Transneptunian objects (TNOs), also known as Kuiper stage of investigation. Advances in instrumentation on tele- belt objects (KBOs) and Edgeworth-Kuiper belt objects scopes of 6- to 10-m aperture have enabled spectroscopic (EKBOs), are presumed to be remnants of the solar nebula studies of an increasing number of these objects, and signifi- that have survived over the age of the solar system. The cant progress is slowly being made. connection of the short-period comets (P < 200 yr) of low We describe here photometric and spectroscopic studies orbital inclination and the transneptunian population of pri- of TNOs and the emerging results.
    [Show full text]
  • Gnc 2021 Abstract Book
    GNC 2021 ABSTRACT BOOK Contents GNC Posters ................................................................................................................................................... 7 Poster 01: A Software Defined Radio Galileo and GPS SW receiver for real-time on-board Navigation for space missions ................................................................................................................................................. 7 Poster 02: JUICE Navigation camera design .................................................................................................... 9 Poster 03: PRESENTATION AND PERFORMANCES OF MULTI-CONSTELLATION GNSS ORBITAL NAVIGATION LIBRARY BOLERO ........................................................................................................................................... 10 Poster 05: EROSS Project - GNC architecture design for autonomous robotic On-Orbit Servicing .............. 12 Poster 06: Performance assessment of a multispectral sensor for relative navigation ............................... 14 Poster 07: Validation of Astrix 1090A IMU for interplanetary and landing missions ................................... 16 Poster 08: High Performance Control System Architecture with an Output Regulation Theory-based Controller and Two-Stage Optimal Observer for the Fine Pointing of Large Scientific Satellites ................. 18 Poster 09: Development of High-Precision GPSR Applicable to GEO and GTO-to-GEO Transfer ................. 20 Poster 10: P4COM: ESA Pointing Error Engineering
    [Show full text]
  • The Dynamics of Plutinos
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server The dynamics of Plutinos Qingjuan Yu and Scott Tremaine Princeton University Observatory, Peyton Hall, Princeton, NJ 08544-1001, USA ABSTRACT Plutinos are Kuiper-belt objects that share the 3:2 Neptune resonance with Pluto. The long-term stability of Plutino orbits depends on their eccentric- ity. Plutinos with eccentricities close to Pluto (fractional eccentricity difference < ∆e=ep = e ep =ep 0:1) can be stable because the longitude difference librates, | − | ∼ in a manner similar to the tadpole and horseshoe libration in coorbital satellites. > Plutinos with ∆e=ep 0:3 can also be stable; the longitude difference circulates ∼ and close encounters are possible, but the effects of Pluto are weak because the encounter velocity is high. Orbits with intermediate eccentricity differences are likely to be unstable over the age of the solar system, in the sense that encoun- ters with Pluto drive them out of the 3:2 Neptune resonance and thus into close encounters with Neptune. This mechanism may be a source of Jupiter-family comets. Subject headings: planets and satellites: Pluto — Kuiper Belt, Oort cloud — celestial mechanics, stellar dynamics 1. Introduction The orbit of Pluto has a number of unusual features. It has the highest eccentricity (ep =0:253) and inclination (ip =17:1◦) of any planet in the solar system. It crosses Neptune’s orbit and hence is susceptible to strong perturbations during close encounters with that planet. However, close encounters do not occur because Pluto is locked into a 3:2 orbital resonance with Neptune, which ensures that conjunctions occur near Pluto’s aphelion (Cohen & Hubbard 1965).
    [Show full text]
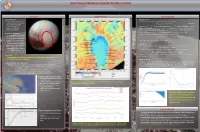
  • Motivation Sputnik Planitia Flexural Modeling Plans for GEOL
    Motivation Sputnik Planitia Flexural modeling Sputnik Planitia Flexure model • Large teardrop-shaped basin The flexure of an elastic plate in two dimensions obeys Equation 1 located on Pluto at 20°N 180°E 푑4푤 퐷 + 푚 − 푐 푔푤 = 푉0 Equation 1. • Size: 1300 km by 900 km 푑푥4 4퐷 1/4 퐸∗ℎ3 • Depth: 3-4 km (basin) where 훼 = is the flexural parameter, 퐷 = is the flexural rigidity, is the 휌 −휌 12(1−푣2) 푚 • 푚 푐 Deposit of nitrogen ice density of the underlying layer of the ice shell, is the density of the ice shell. g is the gravity on • 푐 Water ice basement Pluto, E is the Young’s modulus of water ice, h is the elastic thickness, and 휈 is Poisson’s ratio 푑3푤 1 푑푤 For a single vertical load at 푥 = 0 , the boundary conditions are 퐷 = 푉 and = 0 Formation Hypotheses 푑푥3 2 0 푑푥 • An ancient impact basin created The deflection due to several line loads is found by superposition: 푉 훼3 푥−푥 푥−푥 푥−푥 by an impactor later filled with 푤 = σ 푖 sin 푖 + cos 푖 exp − 푖 Equation 2. 푖 8퐷 훼 훼 훼 N2 ice. The feature would have moved to the current location Where {푉푖} is the magnitude of the loads at position {푥푖} through polar wander. • Runaway deposition of N2 ice Inversion due to albedo feedback at the The load vector 퐕 that produces topography 퐰, is found by least squares optimization: ±30°. The depression is due to 퐕 = 퐌′퐌 + 퐂 −1 퐌′퐰 elastic flexure under the load of 풎 where M is the operator matrix that links a load at position 푥푗 to deflection at a point 푥푖 a thick N2 ice cap.
    [Show full text]
  • Alactic Observer
    alactic Observer G John J. McCarthy Observatory Volume 14, No. 2 February 2021 International Space Station transit of the Moon Composite image: Marc Polansky February Astronomy Calendar and Space Exploration Almanac Bel'kovich (Long 90° E) Hercules (L) and Atlas (R) Posidonius Taurus-Littrow Six-Day-Old Moon mosaic Apollo 17 captured with an antique telescope built by John Benjamin Dancer. Dancer is credited with being the first to photograph the Moon in Tranquility Base England in February 1852 Apollo 11 Apollo 11 and 17 landing sites are visible in the images, as well as Mare Nectaris, one of the older impact basins on Mare Nectaris the Moon Altai Scarp Photos: Bill Cloutier 1 John J. McCarthy Observatory In This Issue Page Out the Window on Your Left ........................................................................3 Valentine Dome ..............................................................................................4 Rocket Trivia ..................................................................................................5 Mars Time (Landing of Perseverance) ...........................................................7 Destination: Jezero Crater ...............................................................................9 Revisiting an Exoplanet Discovery ...............................................................11 Moon Rock in the White House....................................................................13 Solar Beaming Project ..................................................................................14
    [Show full text]
  • CHORUS: Let's Go Meet the Dwarf Planets There Are Five in Our Solar
    Meet the Dwarf Planet Lyrics: CHORUS: Let’s go meet the dwarf planets There are five in our solar system Let’s go meet the dwarf planets Now I’ll go ahead and list them I’ll name them again in case you missed one There’s Pluto, Ceres, Eris, Makemake and Haumea They haven’t broken free from all the space debris There’s Pluto, Ceres, Eris, Makemake and Haumea They’re smaller than Earth’s moon and they like to roam free I’m the famous Pluto – as many of you know My orbit’s on a different path in the shape of an oval I used to be planet number 9, But I break the rules; I’m one of a kind I take my time orbiting the sun It’s a long, long trip, but I’m having fun! Five moons keep me company On our epic journey Charon’s the biggest, and then there’s Nix Kerberos, Hydra and the last one’s Styx 248 years we travel out Beyond the other planet’s regular rout We hang out in the Kuiper Belt Where the ice debris will never melt CHORUS My name is Ceres, and I’m closest to the sun They found me in the Asteroid Belt in 1801 I’m the only known dwarf planet between Jupiter and Mars They thought I was an asteroid, but I’m too round and large! I’m Eris the biggest dwarf planet, and the slowest one… It takes me 557 years to travel around the sun I have one moon, Dysnomia, to orbit along with me We go way out past the Kuiper Belt, there’s so much more to see! CHORUS My name is Makemake, and everyone thought I was alone But my tiny moon, MK2, has been with me all along It takes 310 years for us to orbit ‘round the sun But out here in the Kuiper Belt… our adventures just begun Hello my name’s Haumea, I’m not round shaped like my friends I rotate fast, every 4 hours, which stretched out both my ends! Namaka and Hi’iaka are my moons, I have just 2 And we live way out past Neptune in the Kuiper Belt it’s true! CHORUS Now you’ve met the dwarf planets, there are 5 of them it’s true But the Solar System is a great big place, with more exploring left to do Keep watching the skies above us with a telescope you look through Because the next person to discover one… could be me or you… .
    [Show full text]
  • Quaoar from Multi-Chord Stellar Occultations
    The Astrophysical Journal, 773:26 (13pp), 2013 August 10 doi:10.1088/0004-637X/773/1/26 C 2013. The American Astronomical Society. All rights reserved. Printed in the U.S.A. THE SIZE, SHAPE, ALBEDO, DENSITY, AND ATMOSPHERIC LIMIT OF TRANSNEPTUNIAN OBJECT (50000) QUAOAR FROM MULTI-CHORD STELLAR OCCULTATIONS F. Braga-Ribas1,2,28, B. Sicardy2,3,J.L.Ortiz4, E. Lellouch2, G. Tancredi5, J. Lecacheux2, R. Vieira-Martins1,6,7, J. I. B. Camargo1, M. Assafin7, R. Behrend8,F.Vachier6, F. Colas6, N. Morales4, A. Maury9, M. Emilio10,A.Amorim11, E. Unda-Sanzana12, S. Roland5, S. Bruzzone5, L. A. Almeida13, C. V. Rodrigues13, C. Jacques14, R. Gil-Hutton15, L. Vanzi16,A.C.Milone13, W. Schoenell4,11, R. Salvo5, L. Almenares5,E.Jehin17, J. Manfroid17, S. Sposetti18, P. Tanga19, A. Klotz20, E. Frappa21, P. Cacella22, J. P. Colque12, C. Neves10, E. M. Alvarez23, M. Gillon17, E. Pimentel14, B. Giacchini14, F. Roques2, T. Widemann2, V. S. Magalhaes˜ 13, A. Thirouin4, R. Duffard4, R. Leiva16, I. Toledo24, J. Capeche5, W. Beisker25, J. Pollock26,C.E.Cedeno˜ Montana˜ 13, K. Ivarsen27, D. Reichart27, J. Haislip27, and A. Lacluyze27 1 Observatorio´ Nacional, Rio de Janeiro, Brazil; [email protected] 2 Observatoire de Paris, LESIA, F-92195 Meudon, France 3 Universite´ Pierre et Marie Curie, F-75252 Paris, France 4 Instituto de Astrof´ısica de Andaluc´ıa-CSIC, E-18080 Granada, Spain 5 Observatorio Astronomico Los Molinos, Montevideo U-12400, Uruguay 6 Observatoire de Paris, IMCCE, F-75014 Paris, France 7 Observatorio´ do Valongo/UFRJ, Rio de Janeiro, Brazil 8 Observatoire
    [Show full text]
  • Mass of the Kuiper Belt · 9Th Planet PACS 95.10.Ce · 96.12.De · 96.12.Fe · 96.20.-N · 96.30.-T
    Celestial Mechanics and Dynamical Astronomy manuscript No. (will be inserted by the editor) Mass of the Kuiper Belt E. V. Pitjeva · N. P. Pitjev Received: 13 December 2017 / Accepted: 24 August 2018 The final publication ia available at Springer via http://doi.org/10.1007/s10569-018-9853-5 Abstract The Kuiper belt includes tens of thousands of large bodies and millions of smaller objects. The main part of the belt objects is located in the annular zone between 39.4 au and 47.8 au from the Sun, the boundaries correspond to the average distances for orbital resonances 3:2 and 2:1 with the motion of Neptune. One-dimensional, two-dimensional, and discrete rings to model the total gravitational attraction of numerous belt objects are consid- ered. The discrete rotating model most correctly reflects the real interaction of bodies in the Solar system. The masses of the model rings were determined within EPM2017—the new version of ephemerides of planets and the Moon at IAA RAS—by fitting spacecraft ranging observations. The total mass of the Kuiper belt was calculated as the sum of the masses of the 31 largest trans-neptunian objects directly included in the simultaneous integration and the estimated mass of the model of the discrete ring of TNO. The total mass −2 is (1.97 ± 0.30) · 10 m⊕. The gravitational influence of the Kuiper belt on Jupiter, Saturn, Uranus and Neptune exceeds at times the attraction of the hypothetical 9th planet with a mass of ∼ 10 m⊕ at the distances assumed for it.
    [Show full text]
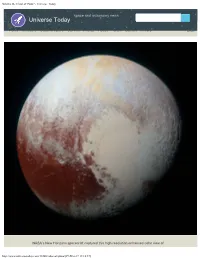
  • What Is the Color of Pluto? - Universe Today
    What is the Color of Pluto? - Universe Today space and astronomy news Universe Today Home Members Guide to Space Carnival Photos Videos Forum Contact Privacy Login NASA’s New Horizons spacecraft captured this high-resolution enhanced color view of http://www.universetoday.com/13866/color-of-pluto/[29-Mar-17 13:18:37] What is the Color of Pluto? - Universe Today Pluto on July 14, 2015. Credit: NASA/JHUAPL/SwRI WHAT IS THE COLOR OF PLUTO? Article Updated: 28 Mar , 2017 by Matt Williams When Pluto was first discovered by Clybe Tombaugh in 1930, astronomers believed that they had found the ninth and outermost planet of the Solar System. In the decades that followed, what little we were able to learn about this distant world was the product of surveys conducted using Earth-based telescopes. Throughout this period, astronomers believed that Pluto was a dirty brown color. In recent years, thanks to improved observations and the New Horizons mission, we have finally managed to obtain a clear picture of what Pluto looks like. In addition to information about its surface features, composition and tenuous atmosphere, much has been learned about Pluto’s appearance. Because of this, we now know that the one-time “ninth planet” of the Solar System is rich and varied in color. Composition: With a mean density of 1.87 g/cm3, Pluto’s composition is differentiated between an icy mantle and a rocky core. The surface is composed of more than 98% nitrogen ice, with traces of methane and carbon monoxide. Scientists also suspect that Pluto’s internal structure is differentiated, with the rocky material having settled into a dense core surrounded by a mantle of water ice.
    [Show full text]
  • Long-Term Orbital and Rotational Motions of Ceres and Vesta T
    A&A 622, A95 (2019) Astronomy https://doi.org/10.1051/0004-6361/201833342 & © ESO 2019 Astrophysics Long-term orbital and rotational motions of Ceres and Vesta T. Vaillant, J. Laskar, N. Rambaux, and M. Gastineau ASD/IMCCE, Observatoire de Paris, PSL Université, Sorbonne Université, 77 avenue Denfert-Rochereau, 75014 Paris, France e-mail: [email protected] Received 2 May 2018 / Accepted 24 July 2018 ABSTRACT Context. The dwarf planet Ceres and the asteroid Vesta have been studied by the Dawn space mission. They are the two heaviest bodies of the main asteroid belt and have different characteristics. Notably, Vesta appears to be dry and inactive with two large basins at its south pole. Ceres is an ice-rich body with signs of cryovolcanic activity. Aims. The aim of this paper is to determine the obliquity variations of Ceres and Vesta and to study their rotational stability. Methods. The orbital and rotational motions have been integrated by symplectic integration. The rotational stability has been studied by integrating secular equations and by computing the diffusion of the precession frequency. Results. The obliquity variations of Ceres over [ 20 : 0] Myr are between 2◦ and 20◦ and the obliquity variations of Vesta are between − 21◦ and 45◦. The two giant impacts suffered by Vesta modified the precession constant and could have put Vesta closer to the resonance with the orbital frequency 2s s . Given the uncertainty on the polar moment of inertia, the present Vesta could be in this resonance 6 − V where the obliquity variations can vary between 17◦ and 48◦.
    [Show full text]
  • 15:1 Resonance Effects on the Orbital Motion of Artificial Satellites
    doi: 10.5028/jatm.2011.03032011 Jorge Kennety S. Formiga* FATEC - College of Technology 15:1 Resonance effects on the São José dos Campos/SP – Brazil [email protected] orbital motion of artificial satellites Rodolpho Vilhena de Moraes Abstract: The motion of an artificial satellite is studied considering Federal University of São Paulo geopotential perturbations and resonances between the frequencies of the São José dos Campos/SP – Brazil mean orbital motion and the Earth rotational motion. The behavior of the [email protected] satellite motion is analyzed in the neighborhood of the resonances 15:1. A suitable sequence of canonical transformations reduces the system of differential equations describing the orbital motion to an integrable kernel. *author for correspondence The phase space of the resulting system is studied taking into account that one resonant angle is fixed. Simulations are presented showing the variations of the semi-major axis of artificial satellites due to the resonance effects. Keywords: Resonance, Artificial satellites, Celestial mechanics. INTRODUCTION some resonance’s region. In our study, it satellites in the neighbourhood of the 15:1 resonance (Fig. 1), or satellites The problem of resonance effects on orbital motion with an orbital period of about 1.6 hours will be considered. of satellites falls under a more categorical problem In our choice, the characteristic of the 356 satellites under in astrodynamics, which is known as the one of zero this condition can be seen in Table 1 (Formiga, 2005). divisors. The influence of resonances on the orbital and translational motion of artificial satellites has been extensively discussed in the literature under several aspects.
    [Show full text]