CBN Journal of Applied Statistics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Human Immunodeficiency and Hepatitis B Viral Co-Infection In
Available online at www.ijmrhs.com cal R edi ese M ar of c l h a & n r H u e o a J l l t h International Journal of Medical Research & a S n ISSN No: 2319-5886 o c i t i Health Sciences, 2020, 9(3): 8-17 e a n n c r e e t s n I • • IJ M R H S Human Immunodeficiency and Hepatitis B Viral Co-infection in Women Attending Antenatal Care Clinic in a Tertiary Health Institution in Nigeria Charles Njoku1,2, Anthony Umego2, Henry Okpara3 and Amarachukwu Njoku2 1Department of Obstetrics and Gynecology, University of Calabar, Nigeria 2Department of Obstetrics and Gynaecology, University of Calabar Teaching Hospital, Calabar, Nigeria 3Department of Chemical Pathology, Nnamdi Azikiwe University, Nnewi Campus, Anambra State, Nigeria *Corresponding e-mail: [email protected] ABSTRACT Background: Human immunodeficiency virus (HIV) and Hepatitis B virus (HBV) infections are major global health problems with common modes of transmission. Objective: To determine the prevalence, demographic characteristics, risk factors and liver dysfunction among antenatal women with HIV and HBV co-infection. Methodology: A cross- sectional study of 586 pregnant women. Socio-demographic data were collected and blood samples were collected and tested for HBsAg and HIV infection. The liver function test was conducted on those who tested positive to HBV alone and have HIV/HBV co-infection. Data were analyzed using SPSS version 18 statistical program. Result: The prevalence of patients with HIV and HBV co-infection was 0.3%. They are single and in the age group of 21-24. -
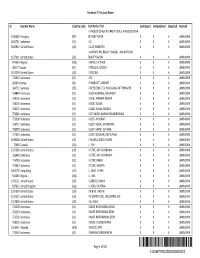
Schedule F-2 by Last Name
Schedule F-2 by Last Name ID Country Name Country Code Last Name, First Contingent Unliquidated Disputed Amount I A NEGOCIOS NA INTERNET LTDA, I A NEGOCIOS NA 1196382 Paraguay (PY) INTERNET LTDA X X X UNKNOWN 1841761 Indonesia (ID) I AK X X X UNKNOWN 1666942 United States (US) I ALZA, ROBERTO X X X UNKNOWN I AM NATURAL BEAUTY SALON, I AM NATURAL 1517291 United States (US) BEAUTY SALON X X X UNKNOWN 949633 Nigeria (NG) I ANYIA, STEPHEN X X X UNKNOWN 820177 Japan (JP) I DEGUCHI, CECILIA X X X UNKNOWN 1517299 United States (US) I DORCIUS X X X UNKNOWN 752343 Indonesia (ID) I EDI X X X UNKNOWN 829494 Kenya (KE) I EMURGAT, AKWARE X X X UNKNOWN 366752 Germany (DE) I FREEE COM LTD, WOLFGANG MITTERMAYR X X X UNKNOWN 754849 Indonesia (ID) I GEDE KOMANG, MALANDO X X X UNKNOWN 748163 Indonesia (ID) I GEDE, AMBARA WIJAYA X X X UNKNOWN 758570 Indonesia (ID) I GEDE, SUSILA X X X UNKNOWN 758571 Indonesia (ID) I GEDE, SUSILA YADNYA X X X UNKNOWN 752381 Indonesia (ID) I GST BAGUS NANDA PARAMESWARA X X X UNKNOWN 752398 Indonesia (ID) I GUSTI AYUSRIATI X X X UNKNOWN 748712 Indonesia (ID) I GUSTI MADE, ARTANAWA X X X UNKNOWN 758579 Indonesia (ID) I GUSTI MADE, SUTAMA X X X UNKNOWN 747655 Indonesia (ID) I GUSTI NGURAH, ADI SUYASA X X X UNKNOWN 1638328 United States (US) I HIULHIU, GUIGLKHGLIU X X X UNKNOWN 72683 Canada (CA) I I, YAY X X X UNKNOWN 1517306 United States (US) I KETUT, ADI SUARBAWA X X X UNKNOWN 752448 Indonesia (ID) I KETUT, ADI SUARBAWA X X X UNKNOWN 753783 Indonesia (ID) I KETUT, KARDI X X X UNKNOWN 759667 Indonesia (ID) I KETUT, WIRATA X -
Creating Markets in Nigeria
A COUNTRY PRIVATE SECTOR DIAGNOSTIC SECTOR PRIVATE COUNTRY A A COUNTRY PRIVATE SECTOR DIAGNOSTIC CREATING MARKETS IN NIGERIA Crowding in the Private Sector: Nigeria’s Path to Faster Job Creation and Structural Transformation October 2020 About IFC IFC—a sister organization of the World Bank and member of the World Bank Group—is the largest global development institution focused on the private sector in emerging markets. We work with more than 2,000 businesses worldwide, using our capital, expertise, and influence to create markets and opportunities in the toughest areas of the world. In fiscal year 2018, we delivered more than $23 billion in long-term financing for developing countries, leveraging the power of the private sector to end extreme poverty and boost shared prosperity. For more information, visit www.ifc.org © International Finance Corporation 2020. All rights reserved. 2121 Pennsylvania Avenue, N.W. Washington, D.C. 20433 www.ifc.org The material in this report was prepared in consultation with government officials and the private sector in Senegal and is copyrighted. Copying and/or transmitting portions or all of this work without permission may be a violation of applicable law. IFC does not guarantee the accuracy, reliability or completeness of the content included in this work, or for the conclusions or judgments described herein, and accepts no responsibility or liability for any omissions or errors (including, without limitation, typographical errors and technical errors) in the content whatsoever or for reliance thereon. The findings, interpretations, views, and conclusions expressed herein are those of the authors and do not necessarily reflect the views of the Executive Directors of the International Finance Corporation or of the International Bank for Reconstruction and Development (the World Bank) or the governments they represent. -

3.2. Project Design 3.2.1
NATIONAL OPEN UNIVERSITY OF NIGERIA 91, Cadastral Zone, University Village Jabi, Abuja FACULTY OF MANAGEMENT SCIENCES DEPARTMENT OF ADMINISTRATION COURSE GUIDE Course Code: MPA 858 Course Title: DEVELOPMENT PLANNING, PROJECT PREPARATION AND IMPLEMENTATION Course Writers: Dr. Ibrahim Adamu Course Editor: Dr. (Mrs.) Yemisi Ogunlela (National Open University of Nigeria) Programme Coordinator: Dr. (Mrs.) Nwamaka P. Ibeme (National Open University of Nigeria) Head of Department: Dr. (Mrs.) Yemisi Ogunlela (National Open University of Nigeria) Dean of Faculty: Dr. Timothy O. Ishola (National Open University of Nigeria) 1 National Open University of Nigeria Headquarters University Village Plot 91 Cadastral Zone NamdiAzikiwe Expressway Jabi, Abuja. Lagos Office 14/16 Ahmadu Bello Way Victoria Island, Lagos e-mail: [email protected] URL: www.nou.edu.ng Published by NOUN Press ©2017 ISBN: All Rights Reserved 2 CONTENTSPAGE Introduction ………………………………………………………… 1 Course Aims …………………………………..…………………......1 CourseObjectives..…………………………………………….……..1 Course Materials……………………………………………………… Study Units ……………………………………..…..………………... Assignments………..………………………………………………... Tutor-Marked Assignment ……………………................................... Final Examination and Grading ……………………….…………… Summary …………………………………………………………… 3 Introduction This course, MPA 858: DEVELOPMENT PLANNING, PROJECT PREPARATION AND IMPLEMENTATION is a two creditunit compulsory course for students studying Public Administration at masters level in the Faculty of Management Sciences. The course -

ISEE 2020 VIRTUAL CONFERENCE Poster Abstract List
ISEE 2020 VIRTUAL CONFERENCE Poster Abstract List Abstract Abstract Title Presenting Author Ref. Number Estimated prenatal exposure to nitrate in drinking water and 1096 body length and head circumference at birth: A population-based Vanessa Renee Coffman prospective cohort study from Denmark, 1991-2011 Estimated prenatal exposure to nitrate in drinking water and 1134 birth defects: A population-based cohort study of over half a Vanessa Renee Coffman million births in Denmark Proximity to freshwater blue space and type 2 diabetes onset: 1135 Melissa N Poulsen the importance of historical and economic context Prospective investigation of urinary polycyclic aromatic hydrocarbon metabolites and mortality in the United States: 1143 Suril S. Mehta National Health and Nutrition Examination Survey (NHANES) and National Death Index (NDI) Linkage (2001-2015) Risk of bias assessments for evidence syntheses of observational 1144 epidemiologic studies of environmental and occupational Kyle Steenland exposures: strengths and limitations Evolution of Evidence on PFOA and Health Following the 1150 Kyle Steenland Assessments of the C8 Science Panel Linking biomarkersof environmental chemical exposure and 1170 endometriosis: integrating the exposome and metabolome in the Komodo Matta ENDOXOMICS-b Study Association of prenatal exposure to phthalates with measures of 1188 Francheska Marie Merced-Nieves cognition in 4.5-month-old infants Long-term exposure to iron and copper in fine particulate air pollution and their combined impact on reactive oxygen species 1207 Zilong Zhang concentration in lung fluid: A population-based cohort study of cardiovascular disease incidence and mortality in Toronto, Canada Plasma concentrations of per- and polyfluoroalkyl substances 1233 Jaclyn A. Janis and body composition from mid-childhood to early adolescence Exploratory Survey of Consumers' Knowledge of Gold Mining: 1240 Afoma Mbanefo Contrasting India and U.S. -

Mise En Page 1
The Africa Experts Ecobank Nigeria Plc Annual Report RC No: 89773 2010 15:27 The Ecobank Network 2 Ecobank Nigeria Annual Report 2010 Ecobank Nigeria branches Head Office Branch Plot 21, Ahmadu Bello Way - P.O. Box 72688, Victoria Island - Lagos - NIGERIA Tel: (234) 1 2710391/5 - Fax: (228) 221 51 19 CROSS RIVER / AKWA IBOM Abak Netpost Ogboefere Market NO 1 Ikot Ekpene Road Abak Tel.: (234) 806 099 7484/704 145 0365; CROSS RIVER STATE Tel.: (234) 07041450461 (234) 803 387 1772/704 145 0254 Old Market Road Calabar II EAST 24 Old Market Road, Onitsha 15, Murtala Mohammed Highway, Tel.: (234) 704 145 0386/704 145 0171 Calabar ABIA STATE Williams Tel.: (234) 803 720 4656/805 839 9981 7 William Street, Onitsha Mary Slessor Factory Road, Aba. Tel.: (234) 704 145 0366/803 335 7444; 12 Mary Slessor Avenue, Calabar No. 1, Factory Road, Aba. (234) 704 145 0907 Tel.: (234) 87 290 474/704 145 0474 Tel.: (234) 07041450398/07041450400 Obudu Ekeoha ENUGU STATE No. 2 Government Station Ranch Road, Ekeoha Shopping Complex, Obudu Ehi/Asa Road, Aba Okpara Avenue I Tel.: (234) 708 987 7826/803 418 6012 Tel.: (234) 704 145 0389; 704 145 0415 31A Okpara Avenue, Enugu Ogoja Govt. Station Layout, Umuahia Tel.: 234) 704 145 0381/704 145 0170; 19 MLA Hospital Road Igoli Ogoja Plot 110 Govt. Station Layout, Umuahia (234) 42 290 578/704 145 0380 Tel.: (234) 08037134913/08028363500 Tel.: (234) 704 145 0411/704 145 0225 Okpara Avenue II Ikom Faulks Road Aba 20B Okpara Avenue, Enugu 72 Calabar Road, Four Corner, Ikom 187 FAULKS ROAD,ABA ABIA-STATE Tel.: (234) 704 145 -

2020 Virtual CONVOCATION CEREMONY
AMERICAN COLLEGE OF SURGEONS 2020 Virtual CONVOCATION CEREMONY SUNDAY, OCTOBER 4, 2020 Congratulations TO ALL OF THE INITIATES OF 2020. Although we can't congratulate you in person, we want to make sure this time is as special for you as past ceremonies. 2 CONTENTS 3 ABOUT THE COLLEGE O The American College of Surgeons (ACS) is the largest organization of surgeons in the world, uniquely positioned to lead the way in optimal patient care, surgical research, health policy, and continuing education and networking opportunities. It is the single strongest voice for surgeons in all specialties and, since its founding in 1913 by surgeons from the United States and Canada, has been at the forefront of providing quality care for surgical patients and supporting surgeons wherever they practice. The College works on behalf of our members and their patients by: Developing innovative educational and training programs to support practicing surgeons, surgery residents, medical students, and surgical team members Improving care for surgical patients through American College of Surgeons Quality Programs, including the Cancer Programs, the Committee on Trauma (COT), and the ACS National Surgical Quality Improvement Program (ACS NSQIP®) Fostering the next generation of promising surgeons through scholarships and fellowships Conducting research to provide cutting-edge best practices in patient care Giving surgeons from across the U.S. and around the globe opportunities for networking Promoting the image of the surgical profession, today and tomorrow The FACS Designation The FACS designation (Fellow, American College of Surgeons) after a surgeon’s name means that the surgeon’s education and training, professional qualifications, surgical competence, and ethical conduct have undergone a rigorous evaluation and have been found to be consistent with the high standards established and demanded by the College. -

XIX FIGO World Congress of Gynecology and Obstetrics 4 – 9 October 2009 Cape Town, South Africa
XIX FIGO World Congress of Gynecology and Obstetrics 4 – 9 October 2009 Cape Town, South Africa Scientific Programme (September 2009) Monday 5 October 09h00 – 10h30 Monday Sessions Auditorium 1 Howard Taylor Lecture Chair: Ralph Hale, Washington DC, USA The Ob-Gyn World is Flat: International Collaboration is Essential for Clinical and Scientific Advances - Joe Leigh Simpson, Houston, USA Auditorium 2 Assisted Reprodutive Technology (ART) in Low-resource Settings Chair: Gamal Serour, Cairo, Egypt Co-chair: Bharati Dhorepatil, Pune, India 1. Demand and Access - Gamal Serour, Cairo, Egypt 2. Stimulation Protocols in Low-resource Settings - Geeta Nargund, London, UK 3. Low Cost ART - Luca Gianaroli, Bologna, Italy 4. Ovarian Hyperstimulation Syndrome and Complications of Art - Thomas D’Hooghe, Leuven, Belgium Ballroom East Caesarean Section Chair: Michael Robson, Dublin, Ireland 1. Auditing Caesarean Section Rates - Michael Robson, Dublin, Ireland 2. Vaginal Birth after Caesarean Section - Gordon Smith, Cambridge, UK 3. Surgical Techniques - Michael Stark, Berlin, Germany Ballroom West New Advances in Surgical Treatment of Cervical Cancer Chair: Desmond Barton, London, UK 1. Sentinel Node in Cervical Cancer: Can It Replace Lymphadenectomy? - Eng Tay, Singapore 2. Role of Laparoscopic Surgery - Dennis Querleu, Toulouse, France 3. Nerve Sparing Operation in Treatment of Cervical Cancer - Desmond Barton, London, UK 4. How Radical Should a Radical Hysterectomy Be? - Prapaporn Suprasert, Chiang Mai, Thailand Westin Grand Ballroom Keynote Lecture Chair: Justo Alonso, Montevideo, Uruguay Appropriate Learning and Technology for Maternal Care in Low Resource Settings - David Woods, Cape Town, South Africa Roof Terrace Non-Physician Human Resources for Major Emergency Obstetric Surgery Chair: Staffan Bergstrom, Stockholm, Sweden 1. -

Technology Ransfer and Commercialization in Nigeria
USEP _____,. Rural Sector Enhancement Program ____________________ Promoting Market-led Agricultural Technology ransfer and Commercialization in Nigeria Editors P.M. Kormawa, C.1. Ezedinma, A.A. Adekunle, and KO. Makinde -,.. IntemationallnslilUle Federal Republic United Slales Agency of Tropical Agriculture of Nigena for In emational lIllAJ Development (U5AIDI Promoting Market-led Agricultural Technology Transfer and Commercialization in Nigeria Edited by P.M. Kormawa, C.I. Ezedinma, AA Adekunle, and KO. Makinde Coordinating Office Rural Sector Enhancement Program International Institute of Tropical Agriculture PMB 5320, Ibadan, Nigeria Acknowledgements We express our profound gratitude to the United States Agency for International Development (USAJD) Nigeria Office who provided the funds for the workshop that led ro the production of these proceedings. Thanks also go to the Winrock International and the Federal Ministry of Agriculture and Rural Development. We are particularly grateful to Mr Ismaila Adamu and Dr O. Oyebanji of the Projects Coordinating Unit for the time they put into the organization of the workshop and launching. We thank all the authors who shared their experiences through the papers presented here. We are also grateful to IITA, especially the Multimedia Unit, for the staff time and resources it invested in producing these proceedings. A special word of thanks should go to Mrs Rose Umelo who, through her editorial prowess, made a lot of sense from several drafts of this document. Dr P. Kormawa Rural Sector Enhancement Program (RUSEP) © IITA 2003 ISBN 976·131·206·6 Citation: Kormawa, P.M., C.I. Ezedinma, A.A. Adekunle, and K.G. Makinde (editors). 2003. Promoting market·led agricultural technology transfer and commercialization in Nigeria. -

Impact of Democratic Governance on Service Delivery in Katsina and Bindawa Local Government Areas of Katsina State
IMPACT OF DEMOCRATIC GOVERNANCE ON SERVICE DELIVERY IN KATSINA AND BINDAWA LOCAL GOVERNMENT AREAS OF KATSINA STATE BY Shehu SANI DEPARTMENT OF PUBLIC ADMINISTRATION, FACULTY OF ADMINISTRATION AHMADU BELLO UNIVERSITY, ZARIA NIGERIA MARCH, 2018 1 IMPACT OF DEMOCRATIC GOVERNANCE ON SERVICE DELIVERY IN KATSINA AND BINDAWA LOCAL GOVERNMENT AREAS OF KATSINA STATE BY Shehu SANI P15ADPA8009 A DISSERTATION SUBMITTED TO THE SCHOOL OF POSTGRADUATE STUDIES, AHMADU BELLO UNIVERSITY, ZARIA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE AWARD OF MASTER OF SCIENCE (MSc) IN PUBLIC ADMINISTRATION, DEPARTMENT OF PUBLIC ADMINISTRATION, FACULTY OF ADMINISTRATION AHMADU BELLO UNIVERSITY, ZARIA, NIGERIA MARCH, 2018 2 DECLARATION I declare that the work in this dissertation entitled ―Impact of Democratic Governance on Service Delivery in Katsina and Bindawa Local Government Areas of Katsina State” has been carried out by me in the Department of Public Administration. The information derived from the literature has been duly acknowledged in the text and a list of references provided. No part of this dissertation was previously presented for another degree or diploma at this or any other institution. Shehu SANI _________________ _________________ _________________ Name of student signature Date CERTIFICATION 3 This dissertation entitled IMPACT OF DEMOCRATIC GOVERNANCE ON SERVICE DELIVERY IN KATSINA AND BINDAWA LOCAL GOVERNMENT AREAS OF KATSINA STATE by shehu SANI meets the regulations governing the award of the degree of Master of Science in Public Administration of the Ahmadu Bello University, and is approved for its contribution to knowledge and literary presentation. Dr Ibrahim Adamu Signature_________________ ______________________________ Date ____________________ Chairman Supervisory Committee Dr Adamu A. Tijjani Signature_________________ ________________________________ Date ____________________ Member Supervisory Committee Dr H. -

Impact of Funding on Quality Education in Ahmadu Bello and Nasarawa Universities, Nigeria 2001-2009 by Tijjani Aliyu Adamu Depar
IMPACT OF FUNDING ON QUALITY EDUCATION IN AHMADU BELLO AND NASARAWA UNIVERSITIES, NIGERIA 2001-2009 BY TIJJANI ALIYU ADAMU DEPARTMENT OF PUBLIC ADMINISTRATION AHMADU BELLO UNIVERSITY, ZARIA NIGERIA. AUGUST 2015 IMPACT OF FUNDING ON QUALITY EDUCATION IN ABU AND NASARAWA UNIVERSITIES, NIGERIA 2001-2009. By TijjaniAliyu ADAMU Ph.D/ADMIN/07085/2006-2007 BEING A DISSERTATION SUBMITTED TO SCHOOL OF POSTGRADUATE STUDIES, AHMADU BELLO UNIVERSITY, ZARIA IN PARTIAL FULFILLMENT OF THE REQUIREMENT FOR THE AWARD OF THE DEGREE OF DOCTOR OF PHILOSOPHY IN PUBLIC ADMINISTRATION AUGUST, 2015 ii DECLARATION I declare that the work in thisThesisentitled “Impact of Funding on Quality Education in ABU and Nasarawa Universities, Nigeria 2001-2009” has been carried out by me in the Department of Public Administration. The information derived from the literature has been duly acknowledged in the text and a list of references provided. No part of this Thesis was previously presented for another degree or diploma at this or any other Institution. __________________ _____________________ _____________________ TijjaniAliyu ADAMU Signature Date iii CERTIFICATION This is to certify that this Thesisentitled IMPACT OF FUNDING ON QUALITY EDUCATION IN AHMADU BELLOAND NASARAWA UNIVERSITIES,NIGERIA 2001- 2009 by TIJJANI,ALIYU ADAMU meets the regulations governing the award of the degree of Doctor of Philosophy (Ph.D) of theAhmadu Bello University, and is approved for its contribution to knowledge and literary presentation. ___________________ ____________ Dr. HarunaYerima Date Chairman, Supervisory Committee ___________________ ____________ Dr. S.B.Abdulkarim Date Member, Supervisory Committee ___________________ ____________ Prof. SaniAbdullahi Date Member, Supervisory Committee ___________________ ____________ Prof. A. Z. Hassan Date Dean, School of Postgraduate iv DEDICATION This Thesis is dedicated to Almighty Allah and our beloved Prophet Mohammed (S.A.W). -

Rural Banditry and Conflicts in Northern Nigeria
RURAL BANDITRY AND CONFLICTS IN NORTHERN NIGERIA CENTRE FOR DEMOCRACY AND DEVELOPMENT EDITED BY: PROF. MOHAMMED J. KUNA & DR. JIBRIN IBRAHIM CENTRE FOR DEMOCRACY AND DEVELOPMENT 1 This Publication was made possible by the following: Centre for Democracy and Development, Pastoral Resolve(PARE) and Nigeria Stability and Reconciliation Programme (NSRP) 2 A Publication of : Centre of Democracy and Development CITECT Estate Abuja E-mail:[email protected] First Published in Nigeria by CDD, 2016 ISBN: 978-978-952-168-5. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmied in any form or means, electronic. mechanical, photocopy, recording or otherwise, without prior wrien permission of CDD 3 Table of Contents FOREWORD 5 PREFACE 7 ACKNOWLEDGEMENT 10 NOTES ON CONTRIBUTORS 11 THE POLITICAL ECONOMY OF RURAL BANDITRY IN CONTEMPORARY NIGERIA 13 CHANGING METHODS OF ANIMAL HUSBANDRY, CATTLE RUSTLING AND RURAL BANDITRY IN NIGERIA 69 THE EFFECT OF ARMED BANDITRY ON RURAL WOMEN'S LIVELIHOOD AND SECURITY: CASE STUDY OF KADUNA & PLATEAU STATES, NIGERIA 111 SOCIAL IMPACT OF RURAL BANDITRY 167 THE STATE OF GRAZING RESERVES AND THEIR POTENTIAL CAPACITY TO ABSORB PASTORALISTS 189 HERDERS' AND FARMERS' ASSOCIATIONS AND SOCIAL CONFLICTS IN NORTHERN NIGERIA 217 RURAL BANDITRY AND HATE SPEECH IN NORTHERN NIGERIA: FERTILE GROUND FOR THE CONSTRUCTION OF DANGEROUS NARRATIVES IN THE MEDIA 257 4 Table of Contents RURAL BANDITRY AND SOCIAL CONFLICTS IN PLATEAU STATE 319 RURAL BANDITRY AND CONFLICTS IN KADUNA STATE, NORTHERN NIGERIA 353 PASTORAL TRANSHUMANCE AND DYNAMICS OF SOCIAL CONFLICT IN NASARAWA STATE, NORTH-CENTRAL NIGERIA 389 5 Foreword This book arose from the concerns of a group of Nigerian civil society activists, academics, development practitioners, politicians and policy makers on the frequent incidence and ravaging impact of violence in rural communities in Northern Nigeria.