C:\Documents and Settings\Holy Cross\Desktop\Repec\Spe\HC Title Page (PM).Wpd
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Public/Social Service/Government
Public/Social Service/Government/Education Elias “Bo” Ackal Jr., member of Louisiana House of Representatives 1972-1996, attended UL Lafayette Ernie Alexander ’64, Louisiana representative 2000-2008 Scott Angelle ’83, secretary of Louisiana Department of Natural Resources Ray Authement ’50, UL Lafayette’s fifth president 1974-2008 Charlotte Beers ’58, former under secretary of U.S. Department of State and former head of two of the largest advertising agencies in the world J. Rayburn Bertrand ’41, mayor of Lafayette 1960-1972 Kathleen Babineaux Blanco ’64, Louisiana’s first female governor 2004-2008; former lieutenant governor, Public Service Commission member, and member of the Louisiana House of Representatives Roy Bourgeois ’62, priest who founded SOA Watch, an independent organization that seeks to close the Western Hemisphere Institute for Security Corporation, a controversial United States military training facility at Fort Benning, Ga. Charles Boustany Jr. ’78, cardiovascular surgeon elected in 2004 to serve as U.S. representative for the Seventh Congressional District Kenny Bowen Sr. ’48, mayor of Lafayette 1972-1980 and 1992-1996 Jack Breaux mayor of Zachary, La., 1966-1980; attended Southwestern Louisiana Institute John Breaux ’66, U.S. senator 1987-2005; U.S. representative 1972-1987, Seventh Congressional District Jefferson Caffery 1903, a member of Southwestern Louisiana Industrial Institute’s first graduating class; served as a U.S. ambassador to El Salvador, Colombia, Cuba, Brazil, France and Egypt 1926-1955 Patrick T. Caffery ’55, U.S. representative for the Third Congressional District 1968- 1971; member of Louisiana House of Representatives 1964-1968 Page Cortez ’86, elected in 2008 to serve in the Louisiana House of Representatives 1 Cindy Courville ’75, professor at the National Defense Intelligence College in Washington, D.C.; first U.S. -

This Bud's for You: Milwaukee Will Take Anything Including The
This Bud’s for you: Milwaukee will take anything including the sleeper tag in order to avoid another 90 loss campaign 6. Milwaukee Brewers: Can Carlos Lee really help the Brewers improve dramatically upon a 67-94 finish one year ago? That’s the major question right now for the baseball team in Milwaukee, which traded base stealer extraordinare Scott Podsednik to the White Sox in exchange for Lee (.305Avg. 31HR 99RBI). He gives them the right handed power bat they’ve been lacking for a while to go sandwiched in between lefty hitters Lyle Overbay (All-Star) and veteran outfielder Geoff Jenkins. Jenkins (.851 career OPS), Lee and likely Brady Clark will compose the Brewers outfield. Behind the plate is Damian Miller, who works very well with start pitchers as he did in Arizona, Oakland and Chicago, so he will have no trouble handling Ben Sheets. Chad Moeller, an ex-teammate of Miller’s with the Diamondbacks, should spell him for about 40-50 games and be a decent backup. I question how good Clark can be in the everyday lineup, markedly as the leadoff man. Clark was decent in 2004, batting .280 and stealing 15 bases. Still, don’t see him staying there long if he’s only score 40-50 runs per season. And Clark will get the chance to touch home plate with guys like Lee, Overbay and Jenkins behind him. Russell Branyan poses a threat when on the field. Despite striking out quite often, he hit 11 dingers in 51 games. Branyan, whose 81 home runs are the most of someone with less than 1500 plate appearances, would relish the opportunity to start every day or get upwards of 250 at-bats. -

December, 2016
By the Numbers Volume 26, Number 2 The Newsletter of the SABR Statistical Analysis Committee December, 2016 Review Academic Research: Three Papers Charlie Pavitt The author reviews three recent academic papers: one investigating the effect of the military draft on the timing of the emergence of young baseball players, another investigating pitch selection over the course of a game, and a third modeling pickoff throws using game theory. I haven’t found any truly outstanding contributions in the attenuated in the last half of careers. It was most evident at the academic literature of late, but here are three I found of some highest production levels; the top ten rWARs and all six Hall of interest. Famers from those birth years were all born on “non-draft days.” Mange, Brennan and David C. Phillips (2016), As some potential players below the “magic number” did not Career interruption and productivity: Evidence serve due to student deferments (among other reasons), and some potential players above the figure did serve as volunteers, these from major league baseball during the figures likely underestimate the actual differences between those Vietnam War who did and did not era , Journal of actually serve. The Human Capital, authors presented Vol. 10, No. 2, In this issue data suggesting that the main reason for pp. 159-185 Academic Research: Three Papers ............................Charlie Pavitt ............................1 this effect may be a World Series Pinch Runners, 1990-2015...................Samuel Anthony........................3 greater likelihood of Mange and Phillips Pitcher Batting Eighth ...............................................Pete Palmer ...............................9 potential players conducted a study of Two Strategies: A Story of Change............................Don Coffin ..............................11 opting for four-year interruptions caused by college rather than draft status during the The previous issue of this publication was March, 2016 (Volume 26, Number 1). -

2017 Information & Record Book
2017 INFORMATION & RECORD BOOK OWNERSHIP OF THE CLEVELAND INDIANS Paul J. Dolan John Sherman Owner/Chairman/Chief Executive Of¿ cer Vice Chairman The Dolan family's ownership of the Cleveland Indians enters its 18th season in 2017, while John Sherman was announced as Vice Chairman and minority ownership partner of the Paul Dolan begins his ¿ fth campaign as the primary control person of the franchise after Cleveland Indians on August 19, 2016. being formally approved by Major League Baseball on Jan. 10, 2013. Paul continues to A long-time entrepreneur and philanthropist, Sherman has been responsible for establishing serve as Chairman and Chief Executive Of¿ cer of the Indians, roles that he accepted prior two successful businesses in Kansas City, Missouri and has provided extensive charitable to the 2011 season. He began as Vice President, General Counsel of the Indians upon support throughout surrounding communities. joining the organization in 2000 and later served as the club's President from 2004-10. His ¿ rst startup, LPG Services Group, grew rapidly and merged with Dynegy (NYSE:DYN) Paul was born and raised in nearby Chardon, Ohio where he attended high school at in 1996. Sherman later founded Inergy L.P., which went public in 2001. He led Inergy Gilmour Academy in Gates Mills. He graduated with a B.A. degree from St. Lawrence through a period of tremendous growth, merging it with Crestwood Holdings in 2013, University in 1980 and received his Juris Doctorate from the University of Notre Dame’s and continues to serve on the board of [now] Crestwood Equity Partners (NYSE:CEQP). -
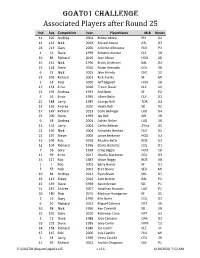
GOAT01 Challenge Associated Players After Round 25
GOAT01 Challenge Associated Players after Round 25 Rnd Seq Competitor Year PlayerName MLB Roster 14 120 Andrea 2004 Bobby Abreu PHI O4 14 124 Nick 2019 Ronald Acuna ATL O2 24 213 Gary 2000 Antonio Alfonseca FLO P3 4 31 Dave 1999 Roberto Alomar CLE 2B 10 86 Richard 2016 Jose Altuve HOU 2B 16 142 Nick 1996 Brady Anderson BAL O4 15 128 Steve 2016 Nolan Arenado COL 3B 6 52 Nick 2015 Jake Arrieta CHC S3 23 203 Richard 2001 Rich Aurilia SF MI 2 18 Rob 2000 Jeff Bagwell HOU 1B 17 153 Ernie 2018 Trevor Bauer CLE S3 22 192 Andrea 1993 Rod Beck SF P2 5 45 Ernie 1995 Albert Belle CLE O2 21 188 Larry 1987 George Bell TOR U2 19 169 Andrea 2010 Heath Bell SD R2 17 149 Richard 2019 Cody Bellinger LAD O4 23 200 Steve 1999 Jay Bell ARI 2B 6 48 Andrea 2004 Adrian Beltre LAD 3B 13 116 Larry 2004 Carlos Beltran 2Tms O5 22 196 Nick 2004 Armando Benitez FLO R2 22 197 Steve 2006 Lance Berkman HOU U2 13 109 Rob 2018 Mookie Betts BOS U1 12 104 Richard 1996 Dante Bichette COL O1 7 58 Gary 1998 Craig Biggio HOU 2B 11 99 Ernie 2017 Charlie Blackmon COL O3 15 127 Rob 1987 Wade Boggs BOS 3B 1 1 Rob 2001 Barry Bonds SF O1 7 57 Nick 2001 Bret Boone SEA MI 10 84 Andrea 2012 Ryan Braun MIL O2 16 143 Steve 2016 Zack Britton BAL P2 16 139 Dave 1998 Kevin Brown SD P1 21 187 Andrea 2007 Jonathan Broxton LAD P1 20 180 Rob 2015 Madison Bumgarner SF S2 2 15 Gary 1996 Ellis Burks COL O2 6 50 Richard 2012 Miguel Cabrera DET 3B 10 88 Nick 1996 Ken Caminiti SD 3B 22 195 Gary 2010 Robinson Cano NYY U2 2 13 Dave 1988 Jose Canseco OAK O2 25 218 Steve 1985 Gary Carter NYM C2 18 158 -

Tony Robichaux 1961-2019
IN MEMORIAM TONY ROBICHAUX 1961-2019 Tony Robichaux spent 25 seasons as the leader of the Louisiana Ragin’ Cajuns and took the baseball program to new heights. Robichaux coached 29 All-Americans, five Academic All-Americans, 90 All-Sun Belt players and 55 All-Louisiana players in his 25 years with the Cajuns. During that time, he coached six Sun Belt Pitchers of the Year, two Sun Belt Players of the Year, two Sun Belt Newcomers of the Year, three Sun Belt Freshmen of the Year, three All-Louisiana Pitchers of the Year, one All-Louisiana Player of the Year and five All-Louisiana Newcomers of the Year. Robichaux took Louisiana to its only College World Series appearance in 2000 and won over 1,000 career games. Yet, that’s not how Robichaux will be remembered. He will be remembered and honored as someone who left behind a legacy of servant leadership and compassion that extended beyond the baseball diamond and into the lives of the thousands of student- athletes and staff he impacted during his career. Coach Robe’s contributions to the University and his impact left on others will not be forgotten. 36 1 WELCOME INTERVIEW AVAILABILITY The Louisiana Athletic Communications Office Head coach Matt Deggs is available at his weekly appreciates your interest in Louisiana Baseball media presss conference and by appointment in and looks forward to assisting you during the the mornings. Check with the Louisiana Athletics 2020 season. Our office is located in the Cox Communications Office for days and times of Communications Building. the weekly media press conferences. -

Atlanta Braves Schedule
2020 60GAME ATLANTA BRAVES SCHEDULE JULYJULY SUN MON TUE WED THU FRI SAT 1 2 3 4 HOME AWAY 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 4:10 25 4:10 26 7:08 27 6:40 28 6:40 29 7:10 30 7:10 31 7:10 AUGUSTAUGUST SUN MON TUE WED THU FRI SAT 1 7:10 2 1:10 3 7:10 4 7:10 5 7:10 6 7:10 7 7:05 8 6:05 9 1:05 10 6:05 11 7:05 12 7:05 13 14 7:10 15 6:10 16 1:10 17 7:10 18 7:10 19 7:10 20 21 7:10 22 7:10 / / / / 23 1:10 24 25 7:10 26 7:10 27 28 7:05 29 1:15 30 7:08 31 7:30 SEPTEMBERSEPTEMBER SUN MON TUE WED THU FRI SAT 1 7:30 2 7:30 3 4 7:10 5 7:10 6 1:10 7 1:10 8 7:10 9 7:10 10 6:05 11 6:05 12 6:05 13 12:35 14 7:35 15 7:35 16 7:35 17 18 7:10 19 7:07 BB&T and SunTrust are now Truist 20 1:10 21 7:10 22 7:10 23 7:10 24 7:10 25 7:10 26 7:10 Together for better 27 3:10 28 29 30 WATCH ON: LISTEN ON: truist.com Truist Bank, Member FDIC. -

10-04-2013 Tigers Game Notes (ALDS Game 1)
Game Information ................................................................................................................................................................................................................................................................................................... Detroit Tigers Media Relations Department w Comerica Park w Phone (313) 471-2000 w Fax (313) 471-2138 w Detroit, MI 48201 w www.tigers.com Detroit Tigers at Oakland Athletics Friday, October 4, 2013 O.co Coliseum, Oakland, CA Game Time - 9:37 p.m. EDT TIGERS AT A GLANCE: The Tigers finished the regular season with an 93-69 record to Tonight’s Scheduled Starters capture the American League Central Division championship. It marks the 15th time in RHP Max Scherzer vs. RHP Bartolo Colon franchise history the Tigers have secured a spot in the playoffs. (21-3, 2.90) (18-6, 2.65) A THIRD STRAIGHT AMERICAN LEAGUE CENTRAL DIVISION TITLE: The Tigers clinched the American League Central Divison for the third straight season and advanced TV/Radio to the playoffs for the 15th time in franchise history. It marks the sixth time the Tigers TBS/97.1 FM have captured a division title since divisional play began during the 1969 season. Detroit has advanced to the playoffs in three consecutive seasons for the second time in club TIGERS VS. ATHLETICS history. The only other time the Tigers have advanced to the playoffs in three consecutive 2013 Record: 3-4 seasons is from 1907-1909. FAMILIAR TERRITORY FOR THE SKIPPER 2013 at Home: 1-3 : Tigers Manager Jim Leyland has guided a 2013 at Oakland: 2-1 club to the postseason for the eighth time in his 22 seasons as a major league manager, including the fourth time during his eight-year tenure with the Tigers. -

Cuban Baseball Players in America: Changing the Difficult Route to Chasing the Dream
CUBAN BASEBALL PLAYERS IN AMERICA: CHANGING THE DIFFICULT ROUTE TO CHASING THE DREAM Evan Brewster* Introduction .............................................................................. 215 I. Castro, United States-Cuba Relations, and The Game of Baseball on the Island ......................................................... 216 II. MLB’s Evolution Under Cuban and American Law Regarding Cuban Baseball Players .................................... 220 III. The Defection Black Market By Sea For Cuban Baseball Players .................................................................................. 226 IV. The Story of Yasiel Puig .................................................... 229 V. The American Government’s and Major League Baseball’s Contemporary Response to Cuban Defection ..................... 236 VI. How to Change the Policies Surrounding Cuban Defection to Major League Baseball .................................................... 239 Conclusion ................................................................................ 242 INTRODUCTION For a long time, the game of baseball tied Cuba and America together. However as relations between the countries deteriorated, so did the link baseball provided between the two countries. As Cuba’s economic and social policies became more restrictive, the best baseball players were scared away from the island nation to the allure of professional baseball in the United States, taking some dangerous and extremely complicated routes * Juris Doctor Candidate, 2017, University of Mississippi -

Weekly Notes 072817
MAJOR LEAGUE BASEBALL WEEKLY NOTES FRIDAY, JULY 28, 2017 BLACKMON WORKING TOWARD HISTORIC SEASON On Sunday afternoon against the Pittsburgh Pirates at Coors Field, Colorado Rockies All-Star outfi elder Charlie Blackmon went 3-for-5 with a pair of runs scored and his 24th home run of the season. With the round-tripper, Blackmon recorded his 57th extra-base hit on the season, which include 20 doubles, 13 triples and his aforementioned 24 home runs. Pacing the Majors in triples, Blackmon trails only his teammate, All-Star Nolan Arenado for the most extra-base hits (60) in the Majors. Blackmon is looking to become the fi rst Major League player to log at least 20 doubles, 20 triples and 20 home runs in a single season since Curtis Granderson (38-23-23) and Jimmy Rollins (38-20-30) both accomplished the feat during the 2007 season. Since 1901, there have only been seven 20-20-20 players, including Granderson, Rollins, Hall of Famers George Brett (1979) and Willie Mays (1957), Jeff Heath (1941), Hall of Famer Jim Bottomley (1928) and Frank Schulte, who did so during his MVP-winning 1911 season. Charlie would become the fi rst Rockies player in franchise history to post such a season. If the season were to end today, Blackmon’s extra-base hit line (20-13-24) has only been replicated by 34 diff erent players in MLB history with Rollins’ 2007 season being the most recent. It is the fi rst stat line of its kind in Rockies franchise history. Hall of Famer Lou Gehrig is the only player in history to post such a line in four seasons (1927-28, 30-31). -

The History of the Fly-By-Night Baseball Association
THE HISTORY OF THE FLY-BY-NIGHT BASEBALL ASSOCIATION PART I Founded in 1974 by David Smith COMMISSIONER 1974 - 78 David Smith 1978 - 80 Craig Haines 1981 - 82 Steve Walters 1983 - 84 Craig Haines 1985 - 87 Steve Walters 1988 to present Rob Bruno PRESIDENTS AMERICAN LEAGUE PRESIDENT NATIONAL LEAGUE PRESIDENT 1985 - 86 Scott Ellis 1985 Bob Cebelak 1987 Mike Kostek 1986 - 87 Rob Bruno 1988 - 89 Bruce Kutler 1988 Joe Hults 1990 - 91 Mike Gereck 1989 Bruce Fogg 1992 - 94 Bob Figella 1990 - 00 Dave Gineo 1995 - 02 Jeff Merklin 2001 to present Bob Figella 2003 –13 Ed Griffin 2014 - 17 Jeff Merklin 2018 to present Ed Griffin WORLD SERIES CHAMPIONS 1975 - West Jeff Jerks NL (wild card) (1) 2000 – Farmington Valley Hawks NL 1976 - Murray Racers NL 2001 - Maine Yaks AL (wild card) 1977 - Galactic Gladiators NL (wild card) 2002 - Caribou Street Hogs NL (3) 1978 - Galactic Gladiators NL 2003 – Hazardville Powderkegs NL 1979 - Illinois Aces AL 2004 – Hazardville Powderkegs NL 2005 – California Dreamers AL 1980 - Carmel Buccaneers NL 2006 – Hart Street Hogs AL 1981 - Galactic Gladiators NL 2007 – Taxachusetts Chiefs NL 1982 - Illinois Aces AL 2008 – Burlington Buccaneers NL 1983 - Illinois Aces AL (wild card) 2009 – Milford Dogfish NL (4) 1984 - Illinois Aces AL (wild card) 2010 – Salem Psychics AL 1985 - Galactic Gladiators NL 1986 - Jupiter Hellbillies AL (wild card) 2011 – Taxachusetts Chiefs NL 1987 - Galactic Gladiators AL 2012 – Salem Psychics AL 1988 - Pawcatuck Pequots NL (wild card) (2) 2013 – Hotlanta Possums (24 Team League) 1989 - Pawcatuck -

Bats 3 Post-Expansion
BATS 3 POST-EXPANSION (1961-to the present) 30 teams 31 players per team 930 total players Names in red are Hall of Famers MVP Most Valuable Player league award ROY Rookie of the Year; league award. CY Cy Young winner league award; CY(M) Cy Young winner when only awarded to best pitcher in the majors NATIONAL LEAGUE MILWAUKEE-ATLANTA BRAVES ARIZONA DIAMONDBACKS CHICAGO CUBS CINCINNATI REDS Hank Aaron – 1971 Jay Bell – 1999 Javier Baez – 2017 Johnny Bench – 1970 MVP Felipe Alou – 1966 Eric Byrnes – 2007 Ernie Banks – 1961 Leo Cardenas – 1966 Jeff Blauser – 1997 Alex Cintron – 2003 Michael Barrett – 2006 Sean Casey – 1999 Rico Carty – 1970 Craig Counsell – 2002 Glenn Beckert – 1971 Dave Concepcion – 1978 Del Crandall – 1962 Stephen Drew – 2008 Kris Bryant – 2016 MVP Eric Davis – 1987 Darrell Evans – 1973 Steve Finley – 2000 Jody Davis – 1983 Adam Dunn – 2004 Freddie Freeman – 2017 Paul Goldschmidt – 2015 Andre Dawson – 1987 MVP George Foster – 1977 MVP Rafael Furcal – 2003 Luis Gonzalez – 2001 Shawon Dunston – 1995 Ken Griffey, Sr. - 1976 Ralph Garr – 1974 Orlando Hudson – 2008 Leon Durham – 1982 Barry Larkin – 1996 Andruw Jones – 2005 Conor Jackson – 2006 Mark Grace – 1995 Lee May – 1969 Chipper Jones – 2008 Jake Lamb – 2016 Jim Hickman – 1970 Devin Mesoraco – 2014 David Justice – 1994 Damian Miller – 2001 Dave Kingman – 1979 Joe Morgan – 1976 MVP Javier Lopez – 2003 Miguel Montero – 2009 Derrek Lee – 2005 Tony Perez – 1970 Brian McCann – 2006 David Peralta – 2015 Anthony Rizzo – 2016 Brandon Phillips – 2007 Fred McGriff – 1994 A.J. Pollock