Combining Computer Models to Account for Mass Loss in Stellar Evolution
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

August 2012 of You Know I Went to the Astronomical League Conference (Alcon) in Chicago at the Beginning of July with My Grandmother
BACKBACK BAYBAY observerobserver The Official Newsletter of the Back Bay Amateur Astronomers P.O. Box 9877, Virginia Beach, VA 23450-9877 Looking Up! Hello again! This month I actually have a story EPHEMERALS to tell, instead of just random ramblings. As most august 2012 of you know I went to the Astronomical League Conference (ALCon) in Chicago at the beginning of July with my grandmother. It was great. Not quite 08/24, 7:00 pm as good as last year, seeing as I had to pay for it Night Hike and they didn’t give me a check and a plaque this Northwest River Park year (last year I won the Horkheimer Youth award, which paid for my trip), but it was still a lot of fun, and very educational. I met a lot of cool 08/24, 8:00 pm people and definitely learned something. The Garden Stars whole trip was a big story, but a few events stand Norfolk Botanical Gardens out the most in my memory, and they’re all connected to some extent. 08/28, 7:00 pm Boardwalk Astronomy It all started on the day we got there. ALCon is Near 24th St Stage an annual four day conference usually in the VA Beach Oceanfront beginning of July. This year, the day we got there was July fourth. After checking in, taking a nap and 09/06, 7:30 pm dining, we decided to participate in the observing BBAA Monthly Meeting event outside the hotel. It was in a parking lot with lights, and fireworks, but there was a large moon TCC Campus and Saturn was up, so we went for it. -

Atlas Menor Was Objects to Slowly Change Over Time
C h a r t Atlas Charts s O b by j Objects e c t Constellation s Objects by Number 64 Objects by Type 71 Objects by Name 76 Messier Objects 78 Caldwell Objects 81 Orion & Stars by Name 84 Lepus, circa , Brightest Stars 86 1720 , Closest Stars 87 Mythology 88 Bimonthly Sky Charts 92 Meteor Showers 105 Sun, Moon and Planets 106 Observing Considerations 113 Expanded Glossary 115 Th e 88 Constellations, plus 126 Chart Reference BACK PAGE Introduction he night sky was charted by western civilization a few thou - N 1,370 deep sky objects and 360 double stars (two stars—one sands years ago to bring order to the random splatter of stars, often orbits the other) plotted with observing information for T and in the hopes, as a piece of the puzzle, to help “understand” every object. the forces of nature. The stars and their constellations were imbued with N Inclusion of many “famous” celestial objects, even though the beliefs of those times, which have become mythology. they are beyond the reach of a 6 to 8-inch diameter telescope. The oldest known celestial atlas is in the book, Almagest , by N Expanded glossary to define and/or explain terms and Claudius Ptolemy, a Greco-Egyptian with Roman citizenship who lived concepts. in Alexandria from 90 to 160 AD. The Almagest is the earliest surviving astronomical treatise—a 600-page tome. The star charts are in tabular N Black stars on a white background, a preferred format for star form, by constellation, and the locations of the stars are described by charts. -

The White Dwarf Cooling Age of the Open Cluster NGC 2420
Publications 9-2000 The White Dwarf Cooling Age of the Open Cluster NGC 2420 Ted von Hippel Embry-Riddle Aeronautical University, [email protected] Gerard Gilmore Institute of Astronomy, Cambridge, [email protected] Follow this and additional works at: https://commons.erau.edu/publication Part of the Stars, Interstellar Medium and the Galaxy Commons Scholarly Commons Citation von Hippel, T., & Gilmore, G. (2000). The White Dwarf Cooling Age of the Open Cluster NGC 2420. The Astronomical Journal, 120(3). Retrieved from https://commons.erau.edu/publication/217 This Article is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Publications by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. THE ASTRONOMICAL JOURNAL, 120:1384È1395, 2000 September ( 2000. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE WHITE DWARF COOLING AGE OF THE OPEN CLUSTER NGC 24201 TED VON HIPPEL Gemini Observatory, 670 North AÏohoku Place, Hilo, HI 96720; ted=gemini.edu AND GERARD GILMORE Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK; gil=ast.cam.ac.uk Received 2000 April 14; accepted 2000 June 1 ABSTRACT We have used deep HST WFPC2 observations of two Ðelds in NGC 2420 to produce a cluster color- magnitude diagram down to V B 27. After imposing morphological selection criteria we Ðnd eight candi- date white dwarfs in NGC 2420. Our completeness estimates indicate that we have found the terminus of the WD cooling sequence. We argue that the cluster distance modulus is likely to be close to 12.10 with E(B[V ) \ 0.04. -

Caldwell Catalogue - Wikipedia, the Free Encyclopedia
Caldwell catalogue - Wikipedia, the free encyclopedia Log in / create account Article Discussion Read Edit View history Caldwell catalogue From Wikipedia, the free encyclopedia Main page Contents The Caldwell Catalogue is an astronomical catalog of 109 bright star clusters, nebulae, and galaxies for observation by amateur astronomers. The list was compiled Featured content by Sir Patrick Caldwell-Moore, better known as Patrick Moore, as a complement to the Messier Catalogue. Current events The Messier Catalogue is used frequently by amateur astronomers as a list of interesting deep-sky objects for observations, but Moore noted that the list did not include Random article many of the sky's brightest deep-sky objects, including the Hyades, the Double Cluster (NGC 869 and NGC 884), and NGC 253. Moreover, Moore observed that the Donate to Wikipedia Messier Catalogue, which was compiled based on observations in the Northern Hemisphere, excluded bright deep-sky objects visible in the Southern Hemisphere such [1][2] Interaction as Omega Centauri, Centaurus A, the Jewel Box, and 47 Tucanae. He quickly compiled a list of 109 objects (to match the number of objects in the Messier [3] Help Catalogue) and published it in Sky & Telescope in December 1995. About Wikipedia Since its publication, the catalogue has grown in popularity and usage within the amateur astronomical community. Small compilation errors in the original 1995 version Community portal of the list have since been corrected. Unusually, Moore used one of his surnames to name the list, and the catalogue adopts "C" numbers to rename objects with more Recent changes common designations.[4] Contact Wikipedia As stated above, the list was compiled from objects already identified by professional astronomers and commonly observed by amateur astronomers. -

The Caldwell Catalogue+Photos
The Caldwell Catalogue was compiled in 1995 by Sir Patrick Moore. He has said he started it for fun because he had some spare time after finishing writing up his latest observations of Mars. He looked at some nebulae, including the ones Charles Messier had not listed in his catalogue. Messier was only interested in listing those objects which he thought could be confused for the comets, he also only listed objects viewable from where he observed from in the Northern hemisphere. Moore's catalogue extends into the Southern hemisphere. Having completed it in a few hours, he sent it off to the Sky & Telescope magazine thinking it would amuse them. They published it in December 1995. Since then, the list has grown in popularity and use throughout the amateur astronomy community. Obviously Moore couldn't use 'M' as a prefix for the objects, so seeing as his surname is actually Caldwell-Moore he used C, and thus also known as the Caldwell catalogue. http://www.12dstring.me.uk/caldwelllistform.php Caldwell NGC Type Distance Apparent Picture Number Number Magnitude C1 NGC 188 Open Cluster 4.8 kly +8.1 C2 NGC 40 Planetary Nebula 3.5 kly +11.4 C3 NGC 4236 Galaxy 7000 kly +9.7 C4 NGC 7023 Open Cluster 1.4 kly +7.0 C5 NGC 0 Galaxy 13000 kly +9.2 C6 NGC 6543 Planetary Nebula 3 kly +8.1 C7 NGC 2403 Galaxy 14000 kly +8.4 C8 NGC 559 Open Cluster 3.7 kly +9.5 C9 NGC 0 Nebula 2.8 kly +0.0 C10 NGC 663 Open Cluster 7.2 kly +7.1 C11 NGC 7635 Nebula 7.1 kly +11.0 C12 NGC 6946 Galaxy 18000 kly +8.9 C13 NGC 457 Open Cluster 9 kly +6.4 C14 NGC 869 Open Cluster -

March Preparing for Your Stargazing Session
Central Coast Astronomical Stargazing March Preparing for your stargazing session: Step 1: Download your free map of the night sky: SkyMaps.com They have it available for Northern and Southern hemispheres. Step 2: Print out this document and use it to take notes during your stargazing session. Step 3: Watch our stargazing video: youtu.be/YewnW2vhxpU *Image credit: all astrophotography images are courtesy of NASA & ESO unless otherwise noted. All planetarium images are courtesy of Stellarium. Main Focus for the Session: 1. Monoceros (the Unicorn) 2. Puppis (the Stern) 3. Vela (the Sails) 4. Carina (the Keel) Notes: Central Coast Astronomy CentralCoastAstronomy.org Page 1 Monoceros (the Unicorn) Monoceros, (the unicorn), meaning “one horn” from the Greek. This is a modern constellation in the northern sky created by Petrus Plancius in 1612. Rosette Nebula is an open cluster plus the surrounding emission nebula. The open cluster is actually denoted NGC 2244, while the surrounding nebulosity was discovered piecemeal by several astronomers and given multiple NGC numbers. This is an area where a cluster of young stars about 3 million years old have blown a hole in the gas and dust where they were born. Hard ultraviolet light from these young stars have excited the gases in the surrounding nebulosity, giving the red wreath-like appearance in photographs. NGC 2244 is in the center of this roughly round nebula. This cluster has a visual magnitude of 4.8 and a distance of about 4900 light years. It was discovered by William Herschel on January 24, 1784. NGC 2244 is about 24’ across and contains about 100 stars. -

Lacaille’S Catalogue of Southern Deep-Sky Objects
Lacaille’s Catalogue of Southern Deep-sky Objects Deep-sky Observing Challenge ASSA Deep-Sky Observing Section. Version 5, 2015 March 12 Lac number Other catalogue designations / Lacaille’s description Object type RA (J2000.0) Dec Con Lac number Other catalogue designations / Lacaille’s description Object type RA (J2000.0) Dec Con Lacaille I.1 NGC 104, 47 Tuc, Dunlop 18, Ben 2, C 106 globular cluster 00 24 06 –72° 04’ 53’’ Tuc Lacaille II.9 IC 2602, Southern Pleiades, C 102 open cluster 10 43 12 –64° 24’ 00’’ Car It resembles the nucleus of a fairly bright small comet. The star Theta Navis, of the third magnitude or less, surrounded by a large number of stars of sixth, seventh and eighth magnitude, which make it resemble the Pleiades. Lacaille I.2 NGC 2070, Tarantula Nebula, Dunlop 142, Ben 35, C 103 bright nebula 05 38 42 –69° 06’ 00’’ Dor It resembles the preceding, but it is fainter. Lacaille II.10 NGC 3532, Pincushion Cluster, Dunlop 323, C 91 open cluster 11 05 33 –58° 43’ 48’’ Car Prodigious cluster of faint stars, very compressed, filling up in the shape of semi-circle of 20’ to 25’ in diameter. Lacaille I.3 NGC 2477, Dunlop 535, C 71 open cluster 07 52 06 –38° 32’ 00’’ Pup Large nebulosity of 15’ to 20’ in diameter. Lacaille II.11 Dunlop 324 asterism 11 22 55 –58° 19’ 36’’ Cen Seven or eight faint stars compressed in a straight line. Lacaille I.4 NGC 4833, Dunlop 164, Ben 56, C 105 globular cluster 12 59 35 –70° 52’ 29’’ Mus It resembles a small comet, faint. -

Number of Objects by Type in the Caldwell Catalogue
Caldwell catalogue Page 1 of 16 Number of objects by type in the Caldwell catalogue Dark nebulae 1 Nebulae 9 Planetary Nebulae 13 Galaxy 35 Open Clusters 25 Supernova remnant 2 Globular clusters 18 Open Clusters and Nebulae 6 Total 109 Caldwell objects Key Star cluster Nebula Galaxy Caldwell Distance Apparent NGC number Common name Image Object type Constellation number LY*103 magnitude C22 NGC 7662 Blue Snowball Planetary Nebula 3.2 Andromeda 9 C23 NGC 891 Galaxy 31,000 Andromeda 10 C28 NGC 752 Open Cluster 1.2 Andromeda 5.7 C107 NGC 6101 Globular Cluster 49.9 Apus 9.3 Page 2 of 16 Caldwell Distance Apparent NGC number Common name Image Object type Constellation number LY*103 magnitude C55 NGC 7009 Saturn Nebula Planetary Nebula 1.4 Aquarius 8 C63 NGC 7293 Helix Nebula Planetary Nebula 0.522 Aquarius 7.3 C81 NGC 6352 Globular Cluster 18.6 Ara 8.2 C82 NGC 6193 Open Cluster 4.3 Ara 5.2 C86 NGC 6397 Globular Cluster 7.5 Ara 5.7 Flaming Star C31 IC 405 Nebula 1.6 Auriga - Nebula C45 NGC 5248 Galaxy 74,000 Boötes 10.2 Page 3 of 16 Caldwell Distance Apparent NGC number Common name Image Object type Constellation number LY*103 magnitude C5 IC 342 Galaxy 13,000 Camelopardalis 9 C7 NGC 2403 Galaxy 14,000 Camelopardalis 8.4 C48 NGC 2775 Galaxy 55,000 Cancer 10.3 C21 NGC 4449 Galaxy 10,000 Canes Venatici 9.4 C26 NGC 4244 Galaxy 10,000 Canes Venatici 10.2 C29 NGC 5005 Galaxy 69,000 Canes Venatici 9.8 C32 NGC 4631 Whale Galaxy Galaxy 22,000 Canes Venatici 9.3 Page 4 of 16 Caldwell Distance Apparent NGC number Common name Image Object type Constellation -

Andromeda Auriga Camelopardalis Canes Vena Cassiopeia Cepheus
Castor NGC 2903 Eurynome Elnath Lemmon (C/2016 X1) M37 Taurus Kalliope M36 PANSTARRS (P/2017 B4) M38 Egeria Auriga Irene Catalina (P/1999 XN120) Menkalinan Honda-Mrkos-Pajdusakova (45P) McNaught (C/2009 F4) Capella Lynx Papagena ValesLeo (P/2010 Minor H2) PANSTARRS (C/2017 C2) PANSTARRS (C/2016 T3)Perseus Tuttle-Giacobini-Kresak (41P) Algol NGC 2403 Catalina (C/2013 US10) Mirfak Siding Spring (C/2013 A1) M34 Boattini (C/2010 U3) Ursa MajorLemmon (C/2012 K8) Camelopardalis Triangulum M81 (Bode's Galaxy) Dubhe Almach NGC 884 (Perseus Double Cluster) NGC 869 (Perseus Double Cluster) NEOWISE (C/2017 C1) M103 NEOWISE (C/2014 N3) PANSTARRS (C/2014 R3) NGC 457 (Owl Cluster) Alioth Polaris Matheny (C/2016 T2) Cassiopeia M63 (Sunflower Galaxy)Canes Venati AndromedaM31 (Andromeda Galaxy) M51 (Whirlpool Galaxy) Kochab Ursa Minor Alkaid M101 (Pinwheel Galaxy) NGC 7789 Catalina (C/2013 V4) M52 (TheCepheus Scorpion) NGC 7662 (Blue Snowball) Catalina (C/2016 KA) Draco PANSTARRS (C/2015 V3) NGC 6946 Lacerta M39 Johnson (C/2015 V2) IRIDIUM 76 [+] IRIDIUM 71 [-] NGC 6826 (Blinking Planetary) NGC 7000 (North America Nebula) TERRA IRAS ARIANE 40+ R/B SL-8 R/B NGC 7027 Deneb M92 Corona Borealis SL-3 R/B SONEAR (C/2014Cygnus A4) Pegasus M13 (Hercules Cluster) PANSTARRS (C/2016 N6)SERT 2 IRIDIUM 70 [+] GP-B Vega IRIDIUM 35 [+] NGC 6992 (Veil Nebula (East), NetworkIRIDIUM Nebula) 31 [+] NGC 6960 (Veil Nebula (West))Lyra SL-3Hercules R/B SL-3 R/B IRIDIUM 53 [+] IRIDIUM 914 [-] ENVISAT IRIDIUM 42 [-] IRIDIUM 33 [-] SL-14 R/B SL-3 R/B Viewing from Burlington, IA; -

Reflectionsreflections the Newsletter of the Popular Astronomy Club
Affiliated with ReflectionsReflections The Newsletter of the Popular Astronomy Club ESTABLISHED 1936 March 2020 President’s Corner MARCH 2020 the newsletter. A small group of us Welcome to anoth- convened at the Paul Castle Memorial er edition of Observatory to view all 27 of the “Reflections”, the Messier objects listed in NCRAL’s Win- universe’s best as- ter Messier Marathon. To my Page Topic knowledge, at this session, three of us 1-2 Presidents tronomy news- Corner letter. It is always a were successful in bagging all 27 of the 3 Announcements/ challenge for me to objects. I am looking forward to ac- Info Alan Sheidler come up with knowledging the achievements of 4-6 Contributions something inter- these observers at a future PAC 6 PAC Outreach esting to pique your interest and get meeting. Congratulations to those in- 7 Awards you to delve further into the news- trepid individuals for stepping up and 8-9 Astronomy in participating. In the meantime, howev- Print letter. I certainly hope my presiden- 10 First Light by tial reflections are not the only rea- er, I would like to ask if anyone else is David Levy son you read PAC’s newsletter. interested in observing these objects? 11 Upcoming Events There is plenty of interesting subject Please let me know if you are. I am 12 Sign Up Report matter here beyond anything I can hoping to have at least one more ob- 13 Astronomical say to entice you to read further. serving session this winter to enable Calendar of folks to observe these objects in a Events/ Rather than taking time here to high- The Planets light this newsletter’s content, this group setting. -
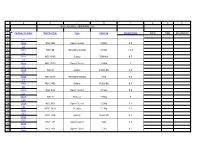
Caldwell Certificate Data
A B C D E F G H 1 CFAS CALDWELL OBSERVING LOG 2 3 Caldwell Number NGC Number Type Distance MAGNITUDE DATE TIME EQUIPMENT 4 5 C1 6 Close NGC 188 Open Cluster 4.8 kly 8.1 7 C2 8 Close NGC 40 Planetary Nebula 3.5 kly 11.4 9 C3 10 Close NGC 4236 Galaxy 7000 kly 9.7 11 C4 12 Close NGC 7023 Open Cluster 1.4 kly 7 13 C5 14 Close NGC 0 Galaxy 13000 kly 9.2 15 C6 16 Close NGC 6543 Planetary Nebula 3 kly 8.1 17 C7 18 Close NGC 2403 Galaxy 14000 kly 8.4 19 C8 20 Close NGC 559 Open Cluster 3.7 kly 9.5 21 C9 22 Close NGC 0 Nebula 2.8 kly 0 23 C10 24 Close NGC 663 Open Cluster 7.2 kly 7.1 25 C11 NGC 7635 Nebula 7.1 kly 11 26 Close 27 C12 NGC 6946 Galaxy 18000 kly 8.9 28 Close 29 C13 NGC 457 Open Cluster 9 kly 6.4 30 Close 31 C14 NGC 869 Open Cluster 7.3 kly 4.3 32 Close A B C D E F G H 33 C15 NGC 6826 Planetary Nebula 2.2 kly 8.8 34 Close 35 C16 NGC 7243 Open Cluster 2.5 kly 6.4 36 Close 37 C17 NGC 147 Galaxy 2300 kly 9.3 38 Close 39 C18 NGC 185 Galaxy 2300 kly 9.2 40 Close 41 C19 NGC 0 Nebula 3.3 kly 7.2 42 Close 43 C20 NGC 7000 Nebula 1.8 kly 0 44 Close 45 C21 NGC 4449 Galaxy 10000 kly 9.4 46 Close 47 C22 NGC 7662 Planetary Nebula 3.2 kly 8.3 48 Close 49 C23 NGC 891 Galaxy 31000 kly 9.9 50 Close 51 C24 NGC 1275 Galaxy 230000 kly 11.6 52 Close 53 C25 NGC 2419 Globular Cluster 275 kly 10.4 54 Close 55 C26 NGC 4244 Galaxy 10000 kly 10.2 56 Close 57 C27 NGC 6888 Nebula 4.7 kly 0 58 Close 59 C28 NGC 752 Open Cluster 1.2 kly 5.7 60 Close 61 C29 NGC 5005 Galaxy 69000 kly 9.8 62 Close 63 C30 NGC 7331 Galaxy 47000 kly 9.5 64 Close A B C D E F G H 65 C31 NGC