DOCSLIB.ORG

Discrete Random Variables

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Random Variables Discrete Random Variables A dichotomous random variable takes only the values 0 and 1. Let X be such a random variable, with Pr(X=1) = p and Pr(X=0) = 1-p . Then E[X] = p, and Var[X] = p(1-p) . Consider a sequence of n independent experiments, each of which has probability p of “being a success.” Let Xk = 1 if the k-th experiment is a success, and 0 otherwise. Then the total number of successes in n trials is X = X1 +...+ Xn ; X is a binomial random variable, and ⎛ n⎞ k n-k Pr(X=k) = ⎜ ⎟ ⋅ p (1 - p ) . ⎝k⎠ E[X] = np , and Var[X] = np(1-p) . (These results follow from the properties of the expected value and variance of sums of independent random variables.) Next, consider a sequence of independent experiments, and let Y be the number of trials up to (and including) the first success. Y is a geometric random variable, and Pr(Y = k) = (1- p)k-1 p . E[Y] = 1/p , and Var[Y] = (1-p)/p2 . (These results follow from the evaluation of infinite sums.) A hypergeometric random variable Z results from drawing a sample of size n from a population of size N containing g “good” members, and then counting the number of “good” members in the sample: ⎛g⎞ ⎛ N − g⎞ ⎜ ⎟ ⎜ ⎟ ⋅⎜ ⎟ ⎝ z⎠ ⎝ n − z ⎠ Pr(Z = z) = . ⎛ N⎞ ⎜ ⎟ ⎝ n ⎠ (This formula was used to compute the relevant probabilities in the “Bag R vs. Bag B” example.) Continuous Random Variables A continuous random variable is a random variable which can take any value in some interval. A continuous random variable is characterized by its probability density function, a graph which has a total area of 1 beneath it: The probability of the random variable taking values in any interval is simply the area under the curve over that interval. The normal distribution: This most-familiar of continuous probability distributions has the classic “bell” shape (see the left-hand graph below). The peak occurs at the mean of the distribution, i.e., at the expected value of the normally-distributed random variable with this distribution, and the standard deviation (the square root of the variance) indicates the spread of the bell, with roughly 68% of the area within 1 standard deviation of the peak. The normal distribution arises so frequently in applications due to an amazing fact: If you take a bunch of independent random variables (with comparable variances) and average them, the result will be roughly normally distributed, no matter what the distributions of the separate variables might be. (This is known as the “Central Limit Theorem”.) Many interesting quantities (ranging from IQ scores, to demand for a retail product, to lengths of shoelaces) are actually a composite of many separate random variables, and hence are roughly normally distributed. If X is normal, and Y = aX+b, then Y is also normal, with E[Y] = a⋅E[X] + b and StdDev[Y] = a⋅StdDev[X] . If X and Y are normal (independent or not), then X+Y and X-Y = X+(-Y) are also normal (intuition: the sum of two bunches is a bunch). Any normally- distributed random variable can be transformed into a “standard” normal random variable (with mean 0 and standard deviation 1) by subtracting off its mean and dividing by its standard deviation. Hence, a single tabulation of the cumulative distribution for a standard normal random variable (attached) can be used to do probabilistic calculations for any normally-distributed random variable. The exponential distribution: Consider the time between successive incoming calls at a switchboard, or between successive patrons entering a store. These “interarrival” times are typically exponentially distributed. If the mean interarrival time is 1/λ (so λ is the mean arrival rate per unit time), then the variance will be 1/λ2 (and the standard deviation will be 1/λ ). The right-hand graph above displays the graph of the exponential density function when λ = 1 . Generally, if X is exponentially distributed, then Pr(s < s < X ≤ t) = e-λs - e-λt (where e ≈ 2.71828) . The exponential distribution fits the examples cited above because it is the only distribution with the “lack-of-memory” property: If X is exponentially distributed, then Pr(X ≤ s+t ⏐X > s) = Pr(X ≤ t). (After waiting a minute without a call, the probability of a call arriving in the next two minutes is the same as was the probability (a minute ago) of getting a call in the following two minutes. As you continue to wait, the chance of something happening “soon” neither increases nor decreases.) Note that, among discrete distributions, the geometric distribution is the only one with the lack-of-memory property; indeed, the exponential and geometric distributions are analogues of one another. Let the time between successive arrivals into some system be exponentially distributed, and let N be the number of arrivals in a fixed interval of time of length t. Then N (a discrete random variable) has the Poisson distribution, and (tλ )k Pr(N=k) = e-tλ ⋅ . k! E[N] = λt, and Var[N] = λt as well. The exponential and Poisson distributions arise frequently in the study of queuing, and of process quality. An interesting (and sometimes useful) fact is that the minimum of two independent, identically-distributed exponential random variables is a new random variable, also exponentially distributed and with a mean precisely half as large as the original mean(s). Connections: The geometric distribution deals with the time between successes in a series of independent trials, and the binomial distribution deals with the number of successes in a fixed number of trials. The exponential distribution deals with the time between occurrences of successive events, and the Poisson distribution deals with the number of occurrences in a fixed period of time. Obviously, there's a relationship here. Rule of thumb: If n > 20 and p < 0.05 , then a binomial random variable with parameters (n, p) has a probability distribution very similar to that of a Poisson random variable with parameters λ = np and t = 1 . (Think of dividing one interval of time into n subintervals, and having a probability p of an arrival in each subinterval. That's very much like having a rate of np arrivals (on average) per unit time.) The uniform distribution: A random variable U is uniformly distributed on an interval [a,b] if its density function is flat over that interval. (The uniform distribution is what one typically has in mind when one thinks of “picking a number at random” over some range.) The expected value of U is (a+b)/2, and Var[U] = (b-a)2/12 . If n independent, identically distributed random variables are all uniformly distributed on [0,1] (i.e., if we pick n numbers at random between 0 and 1), then the expected values of the largest, second-largest,..., smallest are n/(n+1), (n- 1)/(n+1),..., 1/(n+1) (i.e., the expected values divide the interval into n+1 equally-large subintervals). Given that n individuals enter a system (with exponential interarrival times) in a fixed interval of time, the n actual arrival times will look as if they were drawn uniformly over that time interval. The beta distribution: A random variable X has the beta distribution (with parameters α > 0 and β > 0) on the interval [0, 1] if its density has the form k⋅xα−1(1-x)β−1 (where k is a scale factor which makes the area under the curve 1). E[X] = α/(α+β), and Var[X] = αβ/[(α+β)2(α+β+1)] . The main use of the beta distribution is to “fit” it to observed data when building a model of a real-world phenomenon: The beta distribution can take a wide variety of shapes, as seen in the graphs below. The lefthand graph arises when α = 5 and β = 3 , the center when α = 1.5 and β = 3, and the right when α = 0.5 and β = 0.5 . Generally, if α > 2, the density has a slope of 0 at x = 0, if 2 > α > 1, the density is near-vertical near x = 0, and if 1 > α > 0, the density rises as x approaches 0. (Analogous properties involving β hold when x is near 1.) When α = β = 1, the beta distribution is uniform on [0,1]. Right-Tail Probabilities of the Normal Distribution +0.01 +0.02 +0.03 +0.04 +0.05 +0.06 +0.07 +0.08 +0.09 +0.10 0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641 0.4602 0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247 0.4207 0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859 0.3821 0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483 0.3446 0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121 0.3085 0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776 0.2743 0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451 0.2420 0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148 0.2119 0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867 0.1841 0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611 0.1587 1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379 0.1357 1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170 0.1151 1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985 0.0968 1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823 0.0808 1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681 0.0668 1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559 0.0548 1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0.0475 0.0465 0.0455 0.0446 1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367 0.0359 1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294 0.0287 1.9 0.0287 0.0281 0.0274
Load more

Recommended publications
  • Chapter 6 Continuous Random Variables and Probability
    EF 507 QUANTITATIVE METHODS FOR ECONOMICS AND FINANCE FALL 2019 Chapter 6 Continuous Random Variables and Probability Distributions Chap 6-1 Probability Distributions Probability Distributions Ch. 5 Discrete Continuous Ch. 6 Probability Probability Distributions Distributions Binomial Uniform Hypergeometric Normal Poisson Exponential Chap 6-2/62 Continuous Probability Distributions § A continuous random variable is a variable that can assume any value in an interval § thickness of an item § time required to complete a task § temperature of a solution § height in inches § These can potentially take on any value, depending only on the ability to measure accurately. Chap 6-3/62 Cumulative Distribution Function § The cumulative distribution function, F(x), for a continuous random variable X expresses the probability that X does not exceed the value of x F(x) = P(X £ x) § Let a and b be two possible values of X, with a < b. The probability that X lies between a and b is P(a < X < b) = F(b) -F(a) Chap 6-4/62 Probability Density Function The probability density function, f(x), of random variable X has the following properties: 1. f(x) > 0 for all values of x 2. The area under the probability density function f(x) over all values of the random variable X is equal to 1.0 3. The probability that X lies between two values is the area under the density function graph between the two values 4. The cumulative density function F(x0) is the area under the probability density function f(x) from the minimum x value up to x0 x0 f(x ) = f(x)dx 0 ò xm where
    [Show full text]
  • Skewed Double Exponential Distribution and Its Stochastic Rep- Resentation
    EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 2, No. 1, 2009, (1-20) ISSN 1307-5543 – www.ejpam.com Skewed Double Exponential Distribution and Its Stochastic Rep- resentation 12 2 2 Keshav Jagannathan , Arjun K. Gupta ∗, and Truc T. Nguyen 1 Coastal Carolina University Conway, South Carolina, U.S.A 2 Bowling Green State University Bowling Green, Ohio, U.S.A Abstract. Definitions of the skewed double exponential (SDE) distribution in terms of a mixture of double exponential distributions as well as in terms of a scaled product of a c.d.f. and a p.d.f. of double exponential random variable are proposed. Its basic properties are studied. Multi-parameter versions of the skewed double exponential distribution are also given. Characterization of the SDE family of distributions and stochastic representation of the SDE distribution are derived. AMS subject classifications: Primary 62E10, Secondary 62E15. Key words: Symmetric distributions, Skew distributions, Stochastic representation, Linear combina- tion of random variables, Characterizations, Skew Normal distribution. 1. Introduction The double exponential distribution was first published as Laplace’s first law of error in the year 1774 and stated that the frequency of an error could be expressed as an exponential function of the numerical magnitude of the error, disregarding sign. This distribution comes up as a model in many statistical problems. It is also considered in robustness studies, which suggests that it provides a model with different characteristics ∗Corresponding author. Email address: (A. Gupta) http://www.ejpam.com 1 c 2009 EJPAM All rights reserved. K. Jagannathan, A. Gupta, and T. Nguyen / Eur.
    [Show full text]
  • Lecture 2 — September 24 2.1 Recap 2.2 Exponential Families
    STATS 300A: Theory of Statistics Fall 2015 Lecture 2 | September 24 Lecturer: Lester Mackey Scribe: Stephen Bates and Andy Tsao 2.1 Recap Last time, we set out on a quest to develop optimal inference procedures and, along the way, encountered an important pair of assertions: not all data is relevant, and irrelevant data can only increase risk and hence impair performance. This led us to introduce a notion of lossless data compression (sufficiency): T is sufficient for P with X ∼ Pθ 2 P if X j T (X) is independent of θ. How far can we take this idea? At what point does compression impair performance? These are questions of optimal data reduction. While we will develop general answers to these questions in this lecture and the next, we can often say much more in the context of specific modeling choices. With this in mind, let's consider an especially important class of models known as the exponential family models. 2.2 Exponential Families Definition 1. The model fPθ : θ 2 Ωg forms an s-dimensional exponential family if each Pθ has density of the form: s ! X p(x; θ) = exp ηi(θ)Ti(x) − B(θ) h(x) i=1 • ηi(θ) 2 R are called the natural parameters. • Ti(x) 2 R are its sufficient statistics, which follows from NFFC. • B(θ) is the log-partition function because it is the logarithm of a normalization factor: s ! ! Z X B(θ) = log exp ηi(θ)Ti(x) h(x)dµ(x) 2 R i=1 • h(x) 2 R: base measure.
    [Show full text]
  • Statistical Inference
    GU4204: Statistical Inference Bodhisattva Sen Columbia University February 27, 2020 Contents 1 Introduction5 1.1 Statistical Inference: Motivation.....................5 1.2 Recap: Some results from probability..................5 1.3 Back to Example 1.1...........................8 1.4 Delta method...............................8 1.5 Back to Example 1.1........................... 10 2 Statistical Inference: Estimation 11 2.1 Statistical model............................. 11 2.2 Method of Moments estimators..................... 13 3 Method of Maximum Likelihood 16 3.1 Properties of MLEs............................ 20 3.1.1 Invariance............................. 20 3.1.2 Consistency............................ 21 3.2 Computational methods for approximating MLEs........... 21 3.2.1 Newton's Method......................... 21 3.2.2 The EM Algorithm........................ 22 1 4 Principles of estimation 23 4.1 Mean squared error............................ 24 4.2 Comparing estimators.......................... 25 4.3 Unbiased estimators........................... 26 4.4 Sufficient Statistics............................ 28 5 Bayesian paradigm 33 5.1 Prior distribution............................. 33 5.2 Posterior distribution........................... 34 5.3 Bayes Estimators............................. 36 5.4 Sampling from a normal distribution.................. 37 6 The sampling distribution of a statistic 39 6.1 The gamma and the χ2 distributions.................. 39 6.1.1 The gamma distribution..................... 39 6.1.2 The Chi-squared distribution.................. 41 6.2 Sampling from a normal population................... 42 6.3 The t-distribution............................. 45 7 Confidence intervals 46 8 The (Cramer-Rao) Information Inequality 51 9 Large Sample Properties of the MLE 57 10 Hypothesis Testing 61 10.1 Principles of Hypothesis Testing..................... 61 10.2 Critical regions and test statistics.................... 62 10.3 Power function and types of error.................... 64 10.4 Significance level............................
    [Show full text]
  • Likelihood-Based Inference
    The score statistic Inference Exponential distribution example Likelihood-based inference Patrick Breheny September 29 Patrick Breheny Survival Data Analysis (BIOS 7210) 1/32 The score statistic Univariate Inference Multivariate Exponential distribution example Introduction In previous lectures, we constructed and plotted likelihoods and used them informally to comment on likely values of parameters Our goal for today is to make this more rigorous, in terms of quantifying coverage and type I error rates for various likelihood-based approaches to inference With the exception of extremely simple cases such as the two-sample exponential model, exact derivation of these quantities is typically unattainable for survival models, and we must rely on asymptotic likelihood arguments Patrick Breheny Survival Data Analysis (BIOS 7210) 2/32 The score statistic Univariate Inference Multivariate Exponential distribution example The score statistic Likelihoods are typically easier to work with on the log scale (where products become sums); furthermore, since it is only relative comparisons that matter with likelihoods, it is more meaningful to work with derivatives than the likelihood itself Thus, we often work with the derivative of the log-likelihood, which is known as the score, and often denoted U: d U (θ) = `(θjX) X dθ Note that U is a random variable, as it depends on X U is a function of θ For independent observations, the score of the entire sample is the sum of the scores for the individual observations: X U = Ui i Patrick Breheny Survival
    [Show full text]
  • Chapter 10 “Some Continuous Distributions”.Pdf
    CHAPTER 10 Some continuous distributions 10.1. Examples of continuous random variables We look at some other continuous random variables besides normals. Uniform distribution A continuous random variable has uniform distribution if its density is f(x) = 1/(b a) − if a 6 x 6 b and 0 otherwise. For a random variable X with uniform distribution its expectation is 1 b a + b EX = x dx = . b a ˆ 2 − a Exponential distribution A continuous random variable has exponential distribution with parameter λ > 0 if its λx density is f(x) = λe− if x > 0 and 0 otherwise. Suppose X is a random variable with an exponential distribution with parameter λ. Then we have ∞ λx λa (10.1.1) P(X > a) = λe− dx = e− , ˆa λa FX (a) = 1 P(X > a) = 1 e− , − − and we can use integration by parts to see that EX = 1/λ, Var X = 1/λ2. Examples where an exponential random variable is a good model is the length of a telephone call, the length of time before someone arrives at a bank, the length of time before a light bulb burns out. Exponentials are memoryless, that is, P(X > s + t X > t) = P(X > s), | or given that the light bulb has burned 5 hours, the probability it will burn 2 more hours is the same as the probability a new light bulb will burn 2 hours. Here is how we can prove this 129 130 10. SOME CONTINUOUS DISTRIBUTIONS P(X > s + t) P(X > s + t X > t) = | P(X > t) λ(s+t) e− λs − = λt = e e− = P(X > s), where we used Equation (10.1.1) for a = t and a = s + t.
    [Show full text]
  • Package 'Renext'
    Package ‘Renext’ July 4, 2016 Type Package Title Renewal Method for Extreme Values Extrapolation Version 3.1-0 Date 2016-07-01 Author Yves Deville <[email protected]>, IRSN <[email protected]> Maintainer Lise Bardet <[email protected]> Depends R (>= 2.8.0), stats, graphics, evd Imports numDeriv, splines, methods Suggests MASS, ismev, XML Description Peaks Over Threshold (POT) or 'methode du renouvellement'. The distribution for the ex- ceedances can be chosen, and heterogeneous data (including histori- cal data or block data) can be used in a Maximum-Likelihood framework. License GPL (>= 2) LazyData yes NeedsCompilation no Repository CRAN Date/Publication 2016-07-04 20:29:04 R topics documented: Renext-package . .3 anova.Renouv . .5 barplotRenouv . .6 Brest . .8 Brest.years . 10 Brest.years.missing . 11 CV2............................................. 11 CV2.test . 12 Dunkerque . 13 EM.mixexp . 15 expplot . 16 1 2 R topics documented: fgamma . 17 fGEV.MAX . 19 fGPD ............................................ 22 flomax . 24 fmaxlo . 26 fweibull . 29 Garonne . 30 gev2Ren . 32 gof.date . 34 gofExp.test . 37 GPD............................................. 38 gumbel2Ren . 40 Hpoints . 41 ini.mixexp2 . 42 interevt . 43 Jackson . 45 Jackson.test . 46 logLik.Renouv . 47 Lomax . 48 LRExp . 50 LRExp.test . 51 LRGumbel . 53 LRGumbel.test . 54 Maxlo . 55 MixExp2 . 57 mom.mixexp2 . 58 mom2par . 60 NBlevy . 61 OT2MAX . 63 OTjitter . 66 parDeriv . 67 parIni.MAX . 70 pGreenwood1 . 72 plot.Rendata . 73 plot.Renouv . 74 PPplot . 78 predict.Renouv . 79 qStat . 80 readXML . 82 Ren2gev . 84 Ren2gumbel . 85 Renouv . 87 RenouvNoEst . 94 RLlegend . 96 RLpar . 98 RLplot . 99 roundPred . 101 rRendata . 102 Renext-package 3 SandT . 105 skip2noskip .
    [Show full text]
  • 1 IEOR 6711: Notes on the Poisson Process
    Copyright c 2009 by Karl Sigman 1 IEOR 6711: Notes on the Poisson Process We present here the essentials of the Poisson point process with its many interesting properties. As preliminaries, we first define what a point process is, define the renewal point process and state and prove the Elementary Renewal Theorem. 1.1 Point Processes Definition 1.1 A simple point process = ftn : n ≥ 1g is a sequence of strictly increas- ing points 0 < t1 < t2 < ··· ; (1) def with tn−!1 as n−!1. With N(0) = 0 we let N(t) denote the number of points that fall in the interval (0; t]; N(t) = maxfn : tn ≤ tg. fN(t): t ≥ 0g is called the counting process for . If the tn are random variables then is called a random point process. def We sometimes allow a point t0 at the origin and define t0 = 0. Xn = tn − tn−1; n ≥ 1, is called the nth interarrival time. th We view t as time and view tn as the n arrival time (although there are other kinds of applications in which the points tn denote locations in space as opposed to time). The word simple refers to the fact that we are not allowing more than one arrival to ocurr at the same time (as is stated precisely in (1)). In many applications there is a \system" to which customers are arriving over time (classroom, bank, hospital, supermarket, airport, etc.), and ftng denotes the arrival times of these customers to the system. But ftng could also represent the times at which phone calls are received by a given phone, the times at which jobs are sent to a printer in a computer network, the times at which a claim is made against an insurance company, the times at which one receives or sends email, the times at which one sells or buys stock, the times at which a given web site receives hits, or the times at which subways arrive to a station.
    [Show full text]
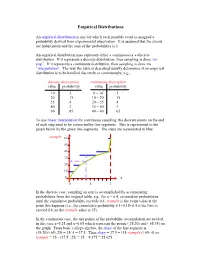
  • Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
    Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph.
    [Show full text]
  • Exponential Families and Theoretical Inference
    EXPONENTIAL FAMILIES AND THEORETICAL INFERENCE Bent Jørgensen Rodrigo Labouriau August, 2012 ii Contents Preface vii Preface to the Portuguese edition ix 1 Exponential families 1 1.1 Definitions . 1 1.2 Analytical properties of the Laplace transform . 11 1.3 Estimation in regular exponential families . 14 1.4 Marginal and conditional distributions . 17 1.5 Parametrizations . 20 1.6 The multivariate normal distribution . 22 1.7 Asymptotic theory . 23 1.7.1 Estimation . 25 1.7.2 Hypothesis testing . 30 1.8 Problems . 36 2 Sufficiency and ancillarity 47 2.1 Sufficiency . 47 2.1.1 Three lemmas . 48 2.1.2 Definitions . 49 2.1.3 The case of equivalent measures . 50 2.1.4 The general case . 53 2.1.5 Completeness . 56 2.1.6 A result on separable σ-algebras . 59 2.1.7 Sufficiency of the likelihood function . 60 2.1.8 Sufficiency and exponential families . 62 2.2 Ancillarity . 63 2.2.1 Definitions . 63 2.2.2 Basu's Theorem . 65 2.3 First-order ancillarity . 67 2.3.1 Examples . 67 2.3.2 Main results . 69 iii iv CONTENTS 2.4 Problems . 71 3 Inferential separation 77 3.1 Introduction . 77 3.1.1 S-ancillarity . 81 3.1.2 The nonformation principle . 83 3.1.3 Discussion . 86 3.2 S-nonformation . 91 3.2.1 Definition . 91 3.2.2 S-nonformation in exponential families . 96 3.3 G-nonformation . 99 3.3.1 Transformation models . 99 3.3.2 Definition of G-nonformation . 103 3.3.3 Cox's proportional risks model .
    [Show full text]
  • 12.4: Exponential and Normal Random Variables Exponential Density Function Given a Positive Constant K > 0, the Exponential Density Function (With Parameter K) Is
    12.4: Exponential and normal random variables Exponential density function Given a positive constant k > 0, the exponential density function (with parameter k) is ke−kx if x ≥ 0 f(x) = 0 if x < 0 1 Expected value of an exponential random variable Let X be a continuous random variable with an exponential density function with parameter k. Integrating by parts with u = kx and dv = e−kxdx so that −1 −kx du = kdx and v = k e , we find Z ∞ E(X) = xf(x)dx −∞ Z ∞ = kxe−kxdx 0 −kx 1 −kx r = lim [−xe − e ]|0 r→infty k 1 = k 2 Variance of exponential random variables Integrating by parts with u = kx2 and dv = e−kxdx so that −1 −kx du = 2kxdx and v = k e , we have Z ∞ Z r 2 −kx 2 −kx r −kx x e dx = lim ([−x e ]|0 + 2 xe dx) 0 r→∞ 0 2 −kx 2 −kx 2 −kx r = lim ([−x e − xe − e ]|0) r→∞ k k2 2 = k2 2 2 2 1 1 So, Var(X) = k2 − E(X) = k2 − k2 = k2 . 3 Example Exponential random variables (sometimes) give good models for the time to failure of mechanical devices. For example, we might measure the number of miles traveled by a given car before its transmission ceases to function. Suppose that this distribution is governed by the exponential distribution with mean 100, 000. What is the probability that a car’s transmission will fail during its first 50, 000 miles of operation? 4 Solution Z 50,000 1 −1 x Pr(X ≤ 50, 000) = e 100,000 dx 0 100, 000 −x 100,000 50,000 = −e |0 −1 = 1 − e 2 ≈ .3934693403 5 Normal distributions The normal density function with mean µ and standard deviation σ is 1 −1 ( x−µ )2 f(x) = √ e 2 σ σ 2π As suggested, if X has this density, then E(X) = µ and Var(X) = σ2.
    [Show full text]
  • 5.2 Exponential Distribution
    Section 5.2. Exponential Distribution 257 5.2 Exponential Distribution A continuous random variable with positive support A = {x|x > 0} is useful in a variety of applica- tions. Examples include • patient survival time after the diagnosis of a particular cancer, • the lifetime of a light bulb, • the sojourn time (waiting time plus service time) for a customer purchasing a ticket at a box office, • the time between births at a hospital, • the number of gallons purchased at a gas pump, or • the time to construct an office building. The common element associated with these random variables is that they can only assume positive values. One fundamental distribution with positive support is the exponential distribution, which is the subject of this section. The gamma distribution also has positive support and is considered in the next section. The exponential distribution has a single scale parameter λ, as defined below. Definition 5.2 A continuous random variable X with probability density function λ f (x)= λe− x x > 0 for some real constant λ > 0 is an exponential(λ) random variable. In many applications, λ is referred to as a “rate,” for example the arrival rate or the service rate in queueing, the death rate in actuarial science, or the failure rate in reliability. The exponential distribution plays a pivotal role in modeling random processes that evolve over time that are known as “stochastic processes.” The exponential distribution enjoys a particularly tractable cumulative distribution function: F(x) = P(X ≤ x) x = f (w)dw Z0 x λ = λe− w dw Z0 λ x = −e− w h i0 λ = 1 − e− x for x > 0.
    [Show full text]