DOCSLIB.ORG

Chapter 1 Magnetic Circuits and Magnetic Materials

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 1 Magnetic Circuits and Magnetic Materials Chapter 1 Magnetic Circuits and Magnetic Materials The objective of this course is to study the devices used in the interconversion of electric and mechanical energy, with emphasis placed on electromagnetic rotating machinery. The transformer, although not an electromechanical-energy-conversion device, is an important component of the overall energy-conversion process. Practically all transformers and electric machinery use ferro-magnetic material for shaping and directing the magnetic fields that acts as the medium for transferring and converting energy. Permanent-magnet materials are also widely used. The ability to analyze and describe systems containing magnetic materials is essential for designing and understanding electromechanical-energy-conversion devices. The techniques of magnetic-circuit analysis, which represent algebraic approximations to exact field-theory solutions, are widely used in the study of electromechanical-energy-conversion devices. §1.1 Introduction to Magnetic Circuits Assume the frequencies and sizes involved are such that the displacement-current term in Maxwell’s equations, which accounts for magnetic fields being produced in space by time-varying electric fields and is associated with electromagnetic radiations, can be neglected. Z H : magnetic field intensity, amperes/m, A/m, A-turn/m, A-t/m Z B : magnetic flux density, webers/m2, Wb/m2, tesla (T) Z 1 Wb =108 lines (maxwells); 1 T =104 gauss Z From (1.1), we see that the source of H is the current density J . The line integral of the tangential component of the magnetic field intensity H around a closed contour C is equal to the total current passing through any surface S linking that contour. O Hdl = O J ⋅ da (1.1) c s Z Equation (1.2) states that the magnetic flux density B is conserved. No net flux enters or leaves a closed surface. There exists no monopole charge sources of magnetic fields. O B ⋅ da = 0 (1.2) s A magnetic circuit consists of a structure composed for the most part of high-permeability magnetic material. The presence of high-permeability material tends to cause magnetic flux to be confined to the paths defined by the structure. Figure 1.1 Simple magnetic circuit. 1 Z In Fig. 1.1, the source of the magnetic field in the core is the ampere-turn product N i , the magnetomotive force (mmf) F acting on the magnetic circuit. Z The magnetic flux φ (in weber, Wb) crossing a surface S is the surface integral of the normal component B : φ = O B ⋅ da (1.3) s Z φ c : flux in core, Bc : flux density in core φ = c Bc Ac (1.4) Z H c : average magnitude H in the core. The direction of H c can be found from the RHR. F = Ni = O Hdl (1.5) = = F Ni H clc (1.6) The relationship between the magnetic field intensity H and the magnetic flux density B : B = μH (1.7) Z Linear relationship? Z μ = μ μ μ r 0 , : magnetic permeability, Wb/A-t-m = H/m Z μ = π × −7 0 4 10 : the permeability of free space Z μ r : relative permeability, typical values: 2000-80,000 A magnetic circuit with an air gap is shown in Fig. 1.2. Air gaps are present for moving elements. The air gap length is sufficiently small. φ : the flux in the magnetic circuit. Figure 1.2 Magnetic circuit with air gap. φ = Bc (1.8) Ac φ = Bg (1.9) Ag = + F H clc H g lg (1.10) B B F = c l + g g (1.11) μ c μ 0 C l g S F = φ D c + T (1.12) D μ μ T E Ac 0 Ag U 2 Z Rc , Rg : the reluctance of the core and the air gap, respectively, l g R = c , R = (1.13), (1.14) c μ g μ Ac 0 Ag = φ( + ) F Rc Rg (1.15) F φ = (1.16) + Rc Rg F φ = (1.17) l c + g μ μ Ac 0 Ag Z In general, for any magnetic circuit of total reluctance Rtot , the flux can be found as F φ = (1.18) Rtot Z The permeance P is the inverse of the reluctance = 1 Ptot (1.19) Rtot Z Fig. 1.3: Analogy between electric and magnetic circuits: Figure 1.3 Analogy between electric and magnetic circuits: (a) electric ckt, (b) magnetic ckt. Z << << Note that with high material permeability: Rc Rg and thus Rtot Rg , F Fμ A μ A φ ≈ = 0 g = Ni 0 g (1.20) Rg g g Z Fig. 1.4: Fringing effect, effective Ag increased. Figure 1.4 Air-gap fringing fields. 3 In general, magnetic circuits can consist of multiple elements in series and parallel. = = = F O Hdl B Fk B H k lk (1.21) k k F = O J ⋅ da (1.22) s = V B Rk ik (1.23) k = Bin 0 (1.24) n φ = B n 0 (1.25) n Figure 1.5 Simple synchronous machine. 4 §1.2 Flux Linkage, Inductance, and Energy Faraday’s Law: d O E ⋅ ds = − O B ⋅ da (1.26) c dt s Z λ : the flux linkage of the winding, ϕ : the instantaneous value of a time-varying flux, Z e : the induced voltage at the winding terminals dϕ dλ e = N = (1.27) dt dt λ = Nϕ (1.28) L : the inductance (with material of constant permeability), H = Wb-t/A λ L = (1.29) i N 2 L = (1.30) Rtot Z The inductance of the winding in Fig. 1.2: N 2 N 2 μ A L = = 0 g (1.31) ()μ g / 0 Ag g Figure 1.6 (a) Magnetic circuit and (b) equivalent circuit for Example 1.3. 5 6 Magnetic circuit with more than one windings, Fig. 1.8: Figure 1.8 Magnetic circuit with two windings. = + F N1i1 N 2i2 (1.32) μ A φ = ()N i + N i 0 c (1.33) 1 1 2 2 g C μ A S C μ A S λ = N φ = N 2 D 0 c T i + N N D 0 c T i (1.34) 1 1 1 E g U 1 1 2 E g U 2 λ = + 1 L11i1 L12i2 (1.35) μ A L = N 2 0 c (1.36) 11 1 g μ A L = N N 0 c = L (1.37) 12 1 2 g 21 C μ A S C μ A S λ = N φ = N N D 0 c T i + N 2 D 0 c T i (1.38) 2 2 1 2 E g U 1 2 E g U 2 λ = + 2 L21i1 L22i2 (1.39) μ A L = N 2 0 c (1.40) 22 2 g Z Induced voltage, power (W = J/s), and stored energy: d e = ()Li (1.41) dt d e = L ()Li (1.42) dt di dL e = L + i (1.43) dt dt dλ p = ie = i (1.44) dt t λ ΔW = 2 p dt = 2 i dλ (1.45) O Oλ t1 1 λ λ 2 2 λ 1 ΔW = i dλ = dλ = ()λ2 − λ2 (1.46) Oλ Oλ 2 1 1 1 L 2L 1 L W = λ2 = i 2 (1.47) 2L 2 7 §1.3 Properties of Magnetic Materials The importance of magnetic materials is twofold: Z Magnetic materials are used to obtain large magnetic flux densities with relatively low levels of magnetizing force. Z Magnetic materials can be used to constrain and direct magnetic fields in well-defined paths. Ferromagnetic materials, typically composed of iron and alloys of iron with cobalt, tungsten, nickel, aluminum, and other metals, are by far the most common magnetic materials. Z They are found to be composed of a large number of domains. Z When unmagnetized, the domain magnetic moments are randomly oriented. Z When an external magnetizing force is applied, the domain magnetic moments tend to align with the applied magnetic field until all the magnetic moments are aligned with the applied field, and the material is said to be fully saturated. Z When the applied field is reduced to zero, the magnetic dipole moments will no longer be totally random in their orientation and will retain a net magnetization component along the applied field direction. The relationship between B and H for a ferromagnetic material is both nonlinear and multivalued. Z In general, the characteristics of the material cannot be described analytically but are commonly presented in graphical form. Z The most common used curve is the B − H curve. Z Dc or normal magnetization curve: Z Hysteresis loop (Note the remanance): 8 Figure 1.9 B-H loops for M-5 grain-oriented electrical steel 0.012 in thick. Only the top halves of the loops are shown here. (Armco Inc.) Figure 1.10 Dc magnetization curve for M-5 grain-oriented electrical steel 0.012 in thick. (Armco Inc.) Figure 1.13 Hysteresis loop. 9 §1.4 AC Excitation In ac power systems, the waveforms of voltage and flux closely approximate sinusoidal functions of time. We are to study the excitation characteristics and losses associated with magnetic materials under steady-state ac operating conditions. Z Assume a sinusoidal variation of the core flux ϕ(t) : ϕ()= φ ω = ω t max sin t Ac Bmax sin t (1.48) φ = ϕ where max amplitude of core flux in webers = Bmax amplitude of flux density Bc in teslas ω = angular frequency = 2πf f = frequency in Hz Z The voltage induced in the N-turn winding is ()= ω φ (ω )= ω e t N max cos t Emax cos t (1.49) E = ωNφ = 2πfNA B max max c max (1.50) Z The Root-Mean-Squared (rms) value: C 1 T S F = D O f 2 ()t dt T (1.51) rms E T o U π = 2 = π Erms fNAc Bmax 2 fNAc Bmax (1.52) 2 Note that the rums value of a sinusoidal wave is 12 times its peak value.
Load more

Recommended publications
  • Design of Magnetic Circuits
    Design of Magnetic Circuits Fundamental Equations Circuit laws similar to those of electric circuits apply in magnetic circuits as well. That is, a magnetic circuit can be replaced by an equivalent electric circuit for Ohm’s Law to be applied. If the magnetomotive force of a magnet is F and the total magnetic flux is Φt, and assuming the magnetic resistance (reluctance) of the circuit is R, then the following equation is valid. （1） Assuming the vacant length of the circuit as ℓg and the vacant cross-sectional area as ag, the magnetic resistance is then given by the following equation. （2） μ is the magnetic permeability of the magnetic path and is equivalent to the magnetic permeability μ0 of a vacuum in the case of air. (μ0=4π×10-7 [H/m]) Yoke 〈Figure 7〉 Although the current in an electric circuit rarely leaks outside the circuit, as the difference in the magnetic permeability between the conductor yoke and insulated area in a magnetic circuit is not very large, leakage of the magnetic flux also becomes large in reality. The amount of the magnetic flux leakage is expressed by the leakage factor σ, which is the ratio of the total magnetic flux Φt generated in the magnetic circuit to the effective magnetic flux Φg of the vacant space. （3） In addition, the loss in the magnetic flux due to the joints in the magnetic circuit must also be taken into consideration. This is represented by the reluctance factor f. Since the leakage factor σ is equivalent to the increase in the vacant space area, and the reluctance factor f refers to the correction coefficient of the vacant space length, the corrected magnetic resistance becomes as follows.
    [Show full text]
  • Transient Simulation of Magnetic Circuits Using the Permeance-Capacitance Analogy
    Transient Simulation of Magnetic Circuits Using the Permeance-Capacitance Analogy Jost Allmeling Wolfgang Hammer John Schonberger¨ Plexim GmbH Plexim GmbH TridonicAtco Schweiz AG Technoparkstrasse 1 Technoparkstrasse 1 Obere Allmeind 2 8005 Zurich, Switzerland 8005 Zurich, Switzerland 8755 Ennenda, Switzerland Email: [email protected] Email: [email protected] Email: [email protected] Abstract—When modeling magnetic components, the R1 Lσ1 Lσ2 R2 permeance-capacitance analogy avoids the drawbacks of traditional equivalent circuits models. The magnetic circuit structure is easily derived from the core geometry, and the Ideal Transformer Lm Rfe energy relationship between electrical and magnetic domain N1:N2 is preserved. Non-linear core materials can be modeled with variable permeances, enabling the implementation of arbitrary saturation and hysteresis functions. Frequency-dependent losses can be realized with resistors in the magnetic circuit. Fig. 1. Transformer implementation with coupled inductors The magnetic domain has been implemented in the simulation software PLECS. To avoid numerical integration errors, Kirch- hoff’s current law must be applied to both the magnetic flux and circuit, in which inductances represent magnetic flux paths the flux-rate when solving the circuit equations. and losses incur at resistors. Magnetic coupling between I. INTRODUCTION windings is realized either with mutual inductances or with ideal transformers. Inductors and transformers are key components in modern power electronic circuits. Compared to other passive com- Using coupled inductors, magnetic components can be ponents they are difficult to model due to the non-linear implemented in any circuit simulator since only electrical behavior of magnetic core materials and the complex structure components are required.
    [Show full text]
  • Magnetism and Magnetic Circuits
    UNIVERSITY OF BABYLON BASIC OF ELECTRICAL ENGINEERING LECTURE NOTES Magnetism and Magnetic Circuits The Nature of a Magnetic Field: Magnetism refers to the force that acts between magnets and magnetic materials. We know, for example, that magnets attract pieces of iron, deflect compass needles, attract or repel other magnets, and so on. The region where the force is felt is called the “field of the magnet” or simply, its magnetic field. Thus, a magnetic field is a force field. Using Faraday’s representation, magnetic fields are shown as lines in space. These lines, called flux lines or lines of force, show the direction and intensity of the field at all points. The field is strongest at the poles of the magnet (where flux lines are most dense), its direction is from north (N) to south (S) external to the magnet, and flux lines never cross. The symbol for magnetic flux as shown is the Greek letter (phi). What happens when two magnets are brought close together? If unlike poles attract, and flux lines pass from one magnet to the other. الصفحة 321 Saad Alwash UNIVERSITY OF BABYLON BASIC OF ELECTRICAL ENGINEERING LECTURE NOTES If like poles repel, and the flux lines are pushed back as indicated by the flattening of the field between the two magnets. Ferromagnetic Materials (magnetic materials that are attracted by magnets such as iron, nickel, cobalt, and their alloys) are called ferromagnetic materials. Ferromagnetic materials provide an easy path for magnetic flux. The flux lines take the longer (but easier) path through the soft iron, rather than the shorter path that they would normally take.
    [Show full text]
  • MAGNETISM and Its Practical Applications
    Mechanical Engineering Laboratory A short introduction to… MAGNETISM and its practical applications Michele Togno – Technical University of Munich, 28 th March 2014 – 4th April 2014 Mechanical Engineering laboratory - Magnetism - 1 - Magnetism A property of matter A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but it is responsible for the most notable property of a magnet: a force that pulls on ferromagnetic materials, such as iron, and attracts or repels other magnets. History of magnetism Magnetite Fe 3O4 Sushruta, VI cen. BCE (lodestone) (Indian surgeon) J.B. Biot, 1774-1862 A.M. Ampere, 1775-1836 Archimedes (287-212 BCE) William Gilbert, 1544-1603 H.C. Oersted, 1777-1851 (English physician) C.F. Gauss, 1777-1855 F. Savart, 1791-1841 M. Faraday, 1791-1867 J.C. Maxwell, 1831-1879 Shen Kuo, 1031-1095 (Chinese scientist) H. Lorentz, 1853-1928 Mechanical Engineering laboratory - Magnetism - 2 - The Earth magnetic field A sort of cosmic shield Mechanical Engineering laboratory - Magnetism - 3 - Magnetic domains and types of magnetic materials Ferromagnetic : a material that could exhibit spontaneous magnetization, that is a net magnetic moment in the absence of an external magnetic field (iron, nickel, cobalt…). Paramagnetic : material slightly attracted by a magnetic field and which doesn’t retain the magnetic properties when the external field is removed (magnesium, molybdenum, lithium…). Diamagnetic : a material that creates a magnetic field in opposition to an externally applied magnetic field (superconductors…). Mechanical Engineering laboratory - Magnetism - 4 - Magnetic field and Magnetic flux Every magnet is a magnetic dipole (magnetic monopole is an hypothetic particle whose existence is not experimentally proven right now).
    [Show full text]
  • Magnetic Theory and Applications.Cdr
    Magnetic Theory & Applications All materials are defined as being magnetic in that they respond to the application of an applied magnetic field differently to that of air or vacuum. Only selected elements or alloys have useful magnetic properties in engineering applications. B Magnetic materials which are easily magnetized and the magnetized are often termed soft. Conversely, those magnetic materials where any induced magnetism Normal is difficult to remove are termed hard or permanent. Intrinsic When a practical or highly permeable material is influenced by an external Initial magnetisation curve magnetic field it may acquire a large magnetization or magnetic induction. The level J of the magnetization will be related to the individual intrinsic permeability of the B HcJ HcB material in question. The relationship between the external field in the induction is: H B = µH where B is the magnetic induction and where µ is the permeability and where H is the external magnetic field. Br Remanence HcB Normal coercivity HcJ Intrinsic coercivity In the S. I. system of units, B is defined in terms of the tesla (T) and the magnetic field H in ampere per meter (A/m). When the external field, H and induction, B are identical (i.e. in a vacuum) the permeability µ is exactly 4π x 10-7 in units of henry per meter for the equation to balance. It is termed µo. Hence: B B = µo H Initial magnetisation curve Bmax In strongly magnetic materials the relationship is: B r A ΔB H B = µ µ H where µ is the relative c o r r H ΔH permeability of the Hysteresis loop material.
    [Show full text]
  • Magnetic Circuits Magnetic Circuit Definitions
    ELG2336: Magnetic Circuits Magnetic Circuit Definitions • Magnetomotive Force – The “driving force” that causes a magnetic field – Symbol, F – Definition, F = NI – Units, Ampere-turns, (A-t) 2 Magnetic Circuit Definitions • Magnetic Field Intensity – mmf gradient, or mmf per unit length – Symbol, H – Definition, H = F/l = NI/l – Units, (A-t/m) 3 Magnetic Circuit Definitions • Flux Density – he concentration of the lines of force in a magnetic circuit – Symbol, B – Definition, B = Φ/A – Units, (Wb/m2), or T (Tesla) 4 Magnetic Circuit Definitions • Reluctance – The measure of “opposition” the magnetic circuit offers to the flux – The analog of Resistance in an electrical circuit – Symbol, R – Definition, R = F/Φ – Units, (A-t/Wb) 5 Magnetic Circuit Definitions • Permeability – Relates flux density and field intensity – Symbol, μ – Definition, μ = B/H – Units, (Wb/A-t-m) ECE 441 6 Magnetic Circuit Definitions • Permeability of free space (air) – Symbol, μ0 -7 – μ0 = 4πx10 Wb/A-t-m 7 Definitions Combined (Unit is Weber (Wb)) = Magnetic Flux Crossing a Surface of Area ‘A’ in m2. B (Unit is Tesla (T)) = Magnetic Flux Density = /A B H (Unit is Amp/m) = Magnetic Field Intensity = = permeability = o r -7 o = 4*10 H/m (H Henry) = Permeability of free space (air) r = Relative Permeability r >> 1 for Magnetic Material 8 Magnetic Circuit 9 Air Gaps, Fringing, and Laminated Cores • Circuits with air gaps may cause fringing • Correction – Increase each cross-sectional dimension of gap by the size of the gap • Many applications use laminated cores
    [Show full text]
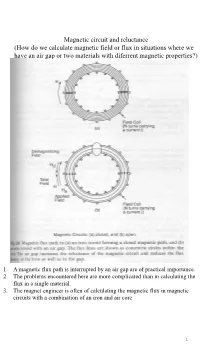
  • Magnetic Circuit and Reluctance (How Do We Calculate Magnetic Field Or
    Magnetic circuit and reluctance (How do we calculate magnetic field or flux in situations where we have an air gap or two materials with diferrent magnetic properties?) 1. A magnetic flux path is interrupted by an air gap are of practical importance. 2. The problems encountered here are more complicated than in calculating the flux in a single material. 3. The magnet engineer is often of calculating the magnetic flux in magnetic circuits with a combination of an iron and air core 1 (i) In closed circuit case ( a ring of iron is wound with N turns of a solenoid which carries a current i) Ni N : Turns Magnetic field H L L : The average length of the ring Flux density passing → Ampere’s law → Ni H dl B μo(H M) circuit in the ring path Ni B μ ( M) Ni HL (B μH) o L B Ni L B B L μ Ni M L μo μ We can define here the magnetomotive N: the number of turns i: the current flowing in the force η which for a solenoid is Ni solenoid A magnetic analogue of flow Ohm’s law We can formulate a general : magnetic flux equation relating the Rm magnetic flux Rm : magnetic relutcance V i i R V Rm R 2 If the iron ring has cross-section area A(m²) permeability μ Turns of solenoid N length L Starting from the B A H A - The term L/μA is the relationship between Ni magnetic reluctance of A path. flux, magnetic induction L and magnetic field Ni - Magnetic reluctance is L series in a magnetic A circuit may be added is analogous to L R R m A A 1 3 Magnetic circuit Electrical circuit magnetomotive force electromotive force Flux () Current (i) reluctance resistance l l Reluctance Resistance R A A 1 Reluctivity Resistivity 1 conductivity permeability (ii) In open circuit case • If the air gap is small, there will be little leakage of the flux at the gap, but B = μH can no longer apply since the μ of air and the iron ring are different.
    [Show full text]
  • Lesson 4: Solving Magnetic Circuits with Electrical Analogies
    8/31/2016 Lesson 4: Solving Magnetic Circuits with Electrical Analogies ET 332a Dc Motors, Generators and Energy Conversion Devices 1 Learning Objectives After this presentation you will be able to: Convert a magnetic structure to a electric circuit analogy Solve a complex magnetic circuit using the mathematical relationships of magnetic circuits Compute the inductance of a coil Define Hysteresis power loss in magnetic circuits and determine power losses. 2 1 8/31/2016 Magnetic-Electric Circuit Analogies Sources = windings and current flowing into coils Core Reluctances = length, area and permeability of core carrying a given flux Air Gap Reluctances = length, area and permeability of free space (air) used to compute these quantities Known flux or Flux Density One of these quantities must be given to find the permeability of core sections. Remember, reluctance is non-linear and depends on the level of flux carried by a core section. 3 Magnetic Circuit Example 3 Converting the magnetic circuit to an electrical analogy The magnetic core at the left has the following core segment lengths L = L = L =L = 1.0 m 0.3 m af cd bc ed Lab=Lfe = 0.8 m 0.5 cm 1.0 m The air gap length is L = 0.5 cm Bag = 0.2 T ag Flux density in the air gap is Bag = 0.2T 0.69 m Coil turns: N =80 t Core cross sectional area: A = 0.04 m2 Coil Resistance: R=2.05 W Fringing negligible 0.8 m 1.0 m 1.) Find battery V to produce Bag 2.) Compute mr for each core leg Using magnetization curve (B-H) from text 4 2 8/31/2016 Example 3 Convert diagram to schematic diagram Rabfe
    [Show full text]
  • Designing Hydraulic-Magnetic Circuit Breakers for Hazardous Rail Applications White Paper WP131005EN Effective January 2017
    Thought leadership White Paper On board with Eaton. Designing hydraulic-magnetic circuit breakers for hazardous rail applications White Paper WP131005EN Effective January 2017 Author name The nature of the rail challenge Alexandre Zint, Conditions on board a train are harsh for equipment mechanically, Product manager, Eaton electrically and environmentally. Additionally, the equipment is expected to endure these conditions throughout near-continuous operation over very long lifetimes. The rail industry is highly competitive, and rail operators Due to space limitations, the electrical equipment is usually tightly are under pressure to make their trains safer, more reliable, packed into small enclosures, cabinets or compartments, with units cost-effective and attractive to travellers. Choosing hydraulic operating in very close proximity to one another. This can increase magnetic circuit breakers for circuit protection can help in the incidence of spikes, transients and bursts in the power lines meeting these objectives, as they perform reliably under that circuit breakers have to protect. Within applications such as the harsh conditions of a rail environment while eliminating metros and tramways, track distances and time intervals between nuisance tripping and its associated problems. In this White stops are short, with multiple journey breaks and traction step Paper Jean-Christophe BARNAS, senior engineer at Eaton changes. These, together with heavy passenger door usage, explains the technology and details the advantages that cause hard repetitive switching which subjects the equipment and it offers. circuit breakers to constant voltage fluctuations. Additionally, there are often long wiring runs between the circuit breakers and the Railways have long been recognised as particularly harsh equipment they protect, because the circuit breakers are usually environments, placing extreme demands on the equipment assembled onto panels within the driver’s cab or into electrical installed into their rolling stock and trackside applications.
    [Show full text]
  • Magnetic Circuits Dr
    1st Class Engineering Collage Basic of Electrical Engineering. Electrical Engineering Dep. Magnetic Circuits Dr. Ibrahim Aljubouri Magnetic Circuits INTRODUCTION Magnetism plays an integral part in almost every electrical device used today in industry, research, or the home. Generators, motors, transformers, circuit breakers, televisions, computers, tape recorders, and telephones all employ magnetic effects to perform a variety of important tasks. MAGNETIC FIELDS In the region surrounding a permanent magnet there exists a magnetic field, which can be represented by magnetic flux lines similar to electric flux lines. Magnetic flux lines, however, do not have origins or terminating points as do electric flux lines but exist in continuous loops, as shown in Figure below. The symbol for magnetic flux is the Greek letter (phi). The magnetic flux lines radiate from the north pole to the south pole, returning to the north pole through the metallic bar. A magnetic field is present around every wire that carries an electric current. The direction of the magnetic flux lines can be found simply by placing the thumb of the right hand in the direction of conventional current flow and noting the direction of the fingers. (This method is commonly called the right-hand rule.) In the SI system of units, magnetic flux is measured in webers. The number of flux lines per unit area is called the flux density, is denoted by the capital letter B, and is measured in teslas. Its magnitude is determined by the following equation: A where is the number of flux lines passing through the area A. Φ Example Determine the flux density PERMEABILITY If cores of different materials with the same physical dimensions are used in the electromagnet described in Section 11.2, the strength of the magnet will vary in accordance with the core used.
    [Show full text]
  • The Study of Magnetic Circuits Is Important in the Study of Energy
    MAGNETIC CIRCUITS The study of magnetic circuits is important in the study of energy systems since the operation of key components such as transformers and rotating machines (DC machines, induction machines, synchronous machines) can be characterized efficiently using magnetic circuits. Magnetic circuits, which characterize the behavior of the magnetic fields within a given device or set of devices, can be analyzed using the circuit analysis techniques defined for electric circuits. The quantities of interest in a magnetic circuit are the vector magnetic field H (A/m), the vector magnetic flux density B (T = Wb/m2) and the total magnetic flux Rm (Wb). The vector magnetic field and vector magnetic flux density are related by where : is defined as the total permeability (H/m), :r is the relative !7 permeability (unitless), and :o = 4B×10 H/m is the permeability of free space. The total magnetic flux through a given surface S is found by integrating the normal component of the magnetic flux density over the surface where the vector differential surface is given by ds = an ds and where an defines a unit vector normal to the surface S. The relative permeability is a measure of how much magnetization occurs within the material. There is no magnetization in free space (vacuum) and negligible magnetization in common conductors such as copper and aluminum. These materials are characterized by a relative permeability of unity (:r =1). There are certain magnetic materials with very high relative permeabilities that are commonly found in components of energy systems. These materials (iron, steel, nickel, cobalt, etc.), designated as ferromagnetic materials, are characterized by significant magnetization.
    [Show full text]
  • Inductor and Transformer Design
    Inductor and Transformer Design 1 Introduction The conditioning of power flow in Power Electronic Systems (PES) is done through the use of elec- tromagnetic elements (inductors and transformers). In this section the basics of electromagnetics is reviewed. They are formulated in such a way as to be useful for the design of inductors and transformers. 2 Electromagnetics The voltage across and the current through a conducting element is related through Ohm’s lam. This law may be stated as follows. When an electric field (of intensity V/m) is set up across a conducting material (of conductivity σ 1/Ω-m), there is an average flow of electrical charges across the conducting material (of current density J A/m). This is shown in Fig. 1. Figure 1 J = σ When expressed in terms of element voltage and current, this reduces to the familiar ststement of Ohm’s law. I = V/R ; R = l/σA In comparison with conducting material, the property of magnetic material may be stated as follows. When a magnetic field (of intensity H A/m) is set up, across a magnetic material (of permeability µ H/m) a magnetic flux (of density B T/m2) is established in the magnetic material, as shown in Fig. 2. B = µH The above equation, in terms of magnetomotive force (mmf = F) and the flux (Φ) in the magnetic circuit, reduces to 1 Figure 2 Φ = F/R ; R = Reluctance of the magnetic circuit l/Aµ The above relationship is analogous to Ohm’s law for magnetic circuits. The magnetic permebility µ of −7 any magnetic material is usually expressed relative to the permeability of free space (µo = 4π × 10 H/m).
    [Show full text]