Computer Aided Sand Wedge Shape Assessment by Using Particle Simulation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

How to Chip It Close
126 CHAPTER 6 STRATEGY How to Chip It Close Land the ball one pace on Determine the yards needed to land the ball one pace and let your club selection on (carry), and the yards from the front edge to the take care of the rest cup (roll), then pull the —Top 100 Teacher Scott Sackett appropriate club based on the chart below. THIS STORY IS THE PROBLEM FOR YOU IF... You’re aware that 1 every chip shot you You’re hit features varying confused by amounts of carry how much and roll, but you carry and roll you need to don’t know how land chips to select clubs or close. adjust your swing 2 to get the right Club Guide (Carry:Roll) You hit every combination for the <1:1 LOB WEDGE chip with your shot you’re facing. sand wedge. 1:1 SAND WEDGE 1:1.5 GAP WEDGE 1:2 PITCHING WEDGE THE SOLUTION >1:2 9-IRON Regardless of how far off the green the ball is sitting, or where the pin is positioned, try to land every chip HOW TO GET THE RIGHT COMBINATION OF CARRY AND ROLL one pace on the front edge of the green. That gives you a baseline Say you’re 10 yards off 15 10 5 0 5 10 15 for determining the exact amount the green, and the pin of carry versus roll for every shot. is cut 10 yards from the TO FLAG TO FLAG TO FLAG (Carry: Roll) (Carry: Roll) (Carry: Roll) Then, using the guide at right, pull front. -

Slice Proof Swing Tony Finau Take the Flagstick Out! Hot List Golf Balls
VOLUME 4 | ISSUE 1 MAY 2019 `150 THINK YOUNG | PLAY HARD PUBLISHED BY SLICE PROOF SWING TONY FINAU TAKE THE FLAGSTICK OUT! HOT LIST GOLF BALLS TIGER’S SPECIAL HERO TRIUMPH INDIAN GREATEST COMEBACK STORY OPEN Exclusive Official Media Partner RNI NO. HARENG/2016/66983 NO. RNI Cover.indd 1 4/23/2019 2:17:43 PM Roush AD.indd 5 4/23/2019 4:43:16 PM Mercedes DS.indd All Pages 4/23/2019 4:45:21 PM Mercedes DS.indd All Pages 4/23/2019 4:45:21 PM how to play. what to play. where to play. Contents 05/19 l ArgentinA l AustrAliA l Chile l ChinA l CzeCh republiC l FinlAnd l FrAnCe l hong Kong l IndIa l indonesiA l irelAnd l KoreA l MAlAysiA l MexiCo l Middle eAst l portugAl l russiA l south AFriCA l spAin l sweden l tAiwAn l thAilAnd l usA 30 46 India Digest Newsmakers 70 18 Ajeetesh Sandhu second in Bangladesh 20 Strong Show By Indians At Qatar Senior Open 50 Chinese Golf On The Rise And Yes Don’t Forget The 22 Celebration of Women’s Golf Day on June 4 Coconuts 54 Els names Choi, 24 Indian Juniors Bring Immelman, Weir as Laurels in Thailand captain’s assistants for 2019 Presidents Cup 26 Club Round-Up Updates from courses across India Features 28 Business Of Golf Industry Updates 56 Spieth’s Nip-Spinner How to get up and down the spicy way. 30 Tournament Report 82 Take the Flagstick Out! Hero Indian Open 2019 by jordan spieth Play Your Best We tested it: Here’s why putting with the pin in 60 Leadbetter’s Laser Irons 75 One Golfer, Three Drives hurts more than it helps. -

Drills and Insight to Slash Your Scores
www.ImagenGolf.com While every precaution has been taken in the preparation of this book, the publisher assumes no responsibility for errors or omissions, or for damages resulting from the use of the information contained herein. THE GOLFER'S PRACTICE PLAN: DRILLS AND INSIGHT TO SLASH YOUR SCORES First edition. January 1, 2019. Copyright © 2021 Imagen Golf. www.ImagenGolf.com Dedicated to my son: I never enjoy the game as much as the rounds we play together! www.ImagenGolf.com Introduction: Why Practice? Golf is a fickle game. It’s based on such a simple principle; simply hole out in as few strokes as possible, but unfortunately, this is much harder than it sounds? So what makes this game so difficult? From my experience, the more I play this game the more I realize that golf’s difficulty comes from the scale of movements and mis-movements that a player makes. While you might think you made the same swing you normally do, a couple millimeters of change above, below, left, or right of the ball at contact can completely change the outcome of your shot. Similarly, two or three degrees of adjustment in how the club strikes the ball can be the difference between your shot flying down the fairway or slicing into the water. This required level of precision, in my opinion, is frustrating for a lot of golfers and is the single biggest limitation of a player’s improvement. Although these small physical changes in each swing dramatically affect your round, this really is what makes the game fun and satisfying to play at a high level. -

Golf Club Prototyping and Design for Spin Rate Tuning
GOLF CLUB PROTOTYPING AND DESIGN FOR SPIN RATE TUNING A Senior Project submitted to the Faculty of California Polytechnic State University, San Luis Obispo In Partial Fulfillment of the Requirements for the Degree of Bachelor of Science in Industrial and Mechanical Engineering by Cole Nygren, Jordan Wright, Jesse Yap June 2017 ABSTRACT Golf Club Prototyping and Design for Spin Rate Tuning Cole Nygren, Jordan Wright, Jesse Yap The aim of this project was to design a golf wedge capable of increasing backspin for the amateur golfer. This was accomplished by embedding a metal lattice structure behind the clubface to allow the face to elastically deform slightly upon impact. This would increase contact time between the club and ball. The mechanism of spin generation was discussed and the relationship between contact time and spin rate was established. The design was enabled by using additive manufacturing, which allowed for the generation of a metal lattice structure. An appropriate control and prototype were designed to minimize run time and material usage due to limited machine capacity. Various lattice topologies were generated and analyzed with finite element analysis. Design validation build in plastic revealed that these were not feasible due to support material generation, so X topology was used instead. After printing, player testing was conducted. The prototype design underwent plastic deformation during testing, and resulted in a significantly lower spin rate than the control. The design outlined in the report is not recommended unless changes to prevent plastic deformation are made and more testing is performed. Economic justification for the production of additive manufacturing golf club designs is made in case future designs prove viable. -

Buyer's Guide to 1966 Golf Clubs
Buyer's Guide to 1966 golf clubs Lost that brochure? Or perhaps one of your members interested in a particular set has "borrowed" and not re- turned it? Now what do you do to satisfy that query about the new, "Super-Duper" wedge put out by ABC Co.? That is just the reason GOLFDOM is offering this "Buyer's guide to 1966 golf clubs." Here in one handy package are the main lines being put out this year by the manufacturers of pro-line clubs. Whether your customer craves a new set of woods or irons, an extra utility club or a new putter, the distinguishing features of any club and its price are at your fingertips. (Addresses of all companies listed are on page 64.) The recent cutback in excise taxes has made it pos- sible for most companies to reduce their prices to the lowest level in years. Make certain you tell your members this wel- come news by any and all means at your disposal—in the club newsletter, your pre-season shop promotion letter, and by word of mouth. Then watch them beat a path to your door! After all, everyone loves a bargain-and how often do you get a bargain on first-quality goods? • PRO LINE EQUIPMENT A NOLO BURTON WOODS IRONS PRICE AVAILABLE PRICE AVAILABLE MODU FEATURES (Set of 1) IN STOCK MODEL FEATURES (Set of 8) IN STOCK < CROOKSHANK Head offset to place striking face $90-$105 Men's 8 CROOKSHANK Angled shaft extends to sole of $235 Men's 8 ROYAL In line with shaft, promoting later (appro».) Ladies' RUSTLESS club, placing weight behind "sweet (approx.) Ladies' SCOTTISH hit with square clubface. -
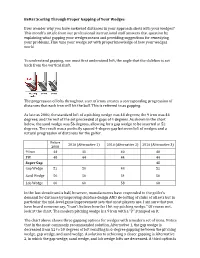
Better Scoring Through Proper Gapping of Your Wedges Ever
Better Scoring Through Proper Gapping of Your Wedges Ever wonder why you have awkward distances in your approach shots with your wedges? This month's article from our professional instructional staff answers that question by explaining what gapping your wedges means and providing suggestions for remedying your problems. Fine tune your wedge set with proper knowledge of how your wedges work! To understand gapping, one must first understand loft, the angle that the clubface is set back from the vertical shaft. The progression of lofts throughout a set of irons creates a corresponding progression of distances that each iron will hit the ball. This is referred to as gapping. As late as 2000, the standard loft of a pitching wedge was 48 degrees; the 9 iron was 44 degrees; and the rest of the set proceeded at gaps of 4 degrees. As shown in the chart below, the sand wedge was 56 degrees, allowing for a gap wedge to be inserted at 52 degrees. The result was a perfectly spaced 4-degree gap between loft of wedges and a natural progression of distances for the golfer. Before 2016 (Alternative 1) 2016 (Alternative 2) 2016 (Alternative 3) 2000 9 Iron 44 40 40 40 PW 48 44 44 44 Super Gap 48 Gap Wedge 52 50 48 52 Sand Wedge 56 56 54 56 Lob Wedge 60 60 58 60 In the last decade and a half, however, manufacturers have responded to the golfer's demand for distance by improving clubface design AND de-lofting of clubs of all sets but in particular the mid-level game improvement sets that most players use. -

Elite Insider Circle Monthly Handicap Improver September 2016
Elite Insider Circle Monthly Handicap Improver September 2016 Hello Fellow Golf Enthusiast, This is Jaacob Bowden. Last Month To recap last month, we had a piece from golf expert Adam Young called “Take Control of Your Game” in which he talked about his teaching process and how he helps students learn how to rectify problems without him even being there. We had a Long Drive Q&A with 4-time World Long Drive Champion Sandra Carlborg of Sweden. Some of the things I think that are worth pointing out about Sandra’s Q&A are: • She tests drivers using a Flightscope launch monitor to help dial in her equipment for maximum distance. • She has swung 117.5 mph in the World Championships. To remind you and give you some perspective on that…male amateurs and LPGA players average around 93 mph and PGA TOUR players average around 113 mph. So as you can see, club head speed is very important for distance. • She spends time in the gym to improve her body’s ability to swing. We see this over and over in these Long Drive Q&A’s. No long hitter of this caliber swings this fast naturally. They all work on their bodies. Fortunately, this is something you can do too at any age or skill level. I talked about my in-person experiences and observations attending this year’s PGA Championship at Baltusrol in New Jersey. From a handicap improving standpoint, a couple of the key things that I was reminded of are: • Lots of different swing styles and techniques can be effective on a global level, even if they aren’t the most optimal. -

Golfer's Guide
THE PGA OF AMERICA FIRST SWING GOLFer’s GUIDE Table of Contents CHAPTER Welcome1 to Golf - 3 CHAPTER Facility Orientation2 - 9 CHAPTER Beginning to Play3 the Game - 13 CHAPTER The Skills4 of Golf - 21 CHAPTER Ball Flight5 Laws - 31 CHAPTER Skill Practice6 - 35 CHAPTER Testing Your7 Skills - 47 CHAPTER Rules of the8 Game - 51 GLOSSARY - 57 FIRST SWING GOLFER’S GUIDE 1 CHAPTER1 Welcome to Golf FIRST SWING GOLFER’S GUIDE 3 CHAPTER 1 WELCOME TO GOLF Dear Golfer Dear Golfer Golf is a challenging and exciting game. The object of moving the ball No experience in the world quite equals the exhilaration you feel when you from a starting point (the teeing ground) to an end point (in the hole) seems hit a golf ball. Whether you’re hitting from the tee, the fairway, the rough simple. But the task of propelling the ball can be complex. The game not or a bunker – when you strike the ball and it goes airborne – it’s the greatest only requires that you attempt to master the multiple skills of golf, but you feeling in the world. must also gain knowledge and understanding about how to play the game. Golf is a game that you will be able to play and enjoy throughout your life- While the game has evolved, the Rules and general nature of the game time. Rich in tradition and history, few sports have a heritage, like golf, that remain unspoiled and we continue to enjoy many of the early elements of can be traced back hundreds of years. -

September 2020 Issue: 7 Drive
SEPTEMBER 2020 ISSUE: 7 DRIVE THE MAGAZINE OF HIDDEN VALLEY GOLF CLUB In this month’s issue 1 BIG FLOP TOURNAMENT RESULTS BUYER BEWARE members will come to see and appreciate the From The President’s camaraderie that the golf club offers. While everything we do at HVGC orbits golf, the real Desk value many of us get is the fellowship, friendship and family aspect of our games, tournaments and social events. For me, as I am sure with many of you, I think of golf as a sport To put it mildly, this has that has gotten me through a lot been a memorable of highs and lows but when I summer at HVGC. really think about it, it's the people I am playing with that In September, I'd like to provide that support, guidance make it a point to ask and oftentimes mentorship. So everyone to take as much for our long time members, take sand as you can out onto a minute to introduce yourself to the course and fill divots. the new faces you see around the We all want the course to club in the coming weeks and be in better shape and months. They are the future of everyone has their ideas HVGC. And to the new members on how to make this all I can say is listen, learn and happen (those board most importantly participate. meetings don't go three Most of the time it might seem hours for nothing) but one like just another round of golf thing we can all do is take but after awhile you'll find that out a sand bottle or ten Eric Kranz when you need a hand, the members at and fill a fairways worth of our club are always happy to help. -

Buyer's Guide to 1967 Golf Clubs
BUYER'S GUIDE TO 1967 GOLF CLUBS PRO LINE EQUIPMENT WOODS ANGLO BURTON IRONS PRICE AVAILABLE PRICE AVAILABLE MODEL FEATURES (Set Of 3) IN STOCK MODEL FEATURES (Set of 8) IN STOCK CROOKSHANK Head offset to place striking $90-$105 Men's & CROOKSHANK Angled shaft extends to sole $188 Men's & ROYAL face in line with shaft promot- (approx.) Ladies' STAINLESS of club placing weight behind Ladies' rt. SCOTTISH ing later hit with square club- rt. & Ift. STEEL "sweet spot." only, face. Shockproof GEODETIC grips, True Temper shafts. PUTTERS UTILITY CLUBS COUNTER- Semi-blade with offset head. $25 Men's rt. SAND WEDGE For shots from sand. All listed Men's & POISE each. are Ladies' rt. PITCHING For shots near green. $23.50 for all WEDGE * each. listed. JIGGER Chipping club. WOODS DUNLOP IRONS PRICE AVAILABLE PRICE AVAILALBLE MODEL FEATURES (Set of 3) IN STOCK MODEL FEATURES (Set of 8) IN STOCK MAXFLI Pear-shaped heads of premier $81 Men's rt. MAXFLI Compact, sharply angled heads, $160 Men's rt. persimmon; weight concentrated slightly curved sole is weighty behind face insert. at bottom. CLASSIC Round-shaped heads made from $56.25 Men's & CLASSIC Heads forged from high-grade $114 Men's & fine persimmon blocks. Ladies' rt. carbon steel alloy. Ladies's rt PAUL HAHN Screwless face inserts, moisture $56.25 Men's rt. PAUL HAHN Hard chrome-plated compact $114 Men's rt. sealed persimmon heads. heads of carbon steel. BOB CHARLES Heads made of hardwood bonded $81 Men's Ift. BOB CHARLES Heads of high-grade carbon $160 Men's Ift. -

PGA Sports Academy Player Level
PGA Sports Academy Player Level 1 PGA Sports Academy Purpose/Mission: The PGA Sports Academy program is a collaborative framework based on research and best practices from PGA Professionals, PGA Education, allied associations and the Long Term Athlete Development (LTAD) standards for juniors adopted by the PGA World Alliance. The PGA Sports Academy’s focus is to develop core golfers and provide them with pathways to continue to play golf socially or competitively based on each individual’s desire. It is imperative that every parent/participant understands the process of LTAD in the PGA Sports Academy program so that they have a clear understanding of what the PGA Professional is trying to accomplish with each participant. PGA Professionals are strongly encouraged to distribute a copy of The PGA Sports Academy Parent Resource to parents before their child begins the PGA Sports Academy to help outline the curriculum and expectations for the program. Fun – First And Foremost Fun – First and Foremost is our junior golf mantra. We must make sure new golfers are engaged and have a fun, interactive experience. To educate and get juniors involved in golf is the goal, but keeping it fun is the primary focus. It’s crucial that instructors enjoy the experience— juniors will sense your love of the sport and hopefully become smitten for a lifetime. PGA Sports Academy Curriculum Overview: The PGA Sports Academy will help youth learn to play golf and have fun in the process. The PGA Sports Academy has three levels: Player, Sport and Champion. Player Level Objectives • Develop an understanding of the sport of golf; • Learn fundamental movement and motor skills and link them together into the golf swing; • Use ball-striking games such as baseball and hockey to develop hand-eye coordination; • Establish essential safety and etiquette. -

Golf Club Terminology
golf club terminology Attack Wedge Over time the difference between the average loft of a pitching wedge and a sand wedge has increased, creating a significant void between them. The attack wedge was created to fill that void; its loft is approximately halfway between the pitching wedge and sand wedge. Bounce Bounce refers to the shape of an iron’s sole. A club whose sole protrudes below the leading edge of the club is said to have positive bounce, while a club whose sole is level with the leading edge and parallel to the ground at address is said to have zero bounce. Positive bounce is useful for preventing the clubface from digging deeply into the turf, and is especially useful for playing explosion shots from sand because it helps the clubhead bounce upward and out of the sand instead of digging downward. Center of Gravity (CG) Center of Gravity, or “CG,” is the point in the clubhead where all lines of balance intersect, and where the entire mass is at equilibrium in all directions. CG position usually affects launch angle. Generally, the higher the CG (farther from the ground), the lower the launch angle. By strategically distributing the weight in the clubhead, club designers can position the CG lower and farther back in the clubhead to produce a higher launch angle, which generally results in more carry and greater distance. Clubface The area of the clubhead, be it a wood, hybrid, iron or putter, that’s used to strike the ball. CNC Milling Milling is a process of cutting metal to achieve a specific type of shape or surface.