DOCSLIB.ORG

Shipping Derivatives and Risk Management

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Shipping Derivatives and Risk Management Shipping Derivatives and Risk Management Amir H. Alizadeh & Nikos K. Nomikos Faculty of Finance, Cass Business School, City University, London palgrave macmiUan Contents About the Authors . xv Preface and Acknowledgements xvi Foreword xviii Figures xix Tables xxv Chapter 1: Introduction to Risk Management and Derivatives 1 1.1 Introduction 1 1.2 Types of risks facing shipping companies 3 1.3 The risk-management process 6 1.3.1 Why should firms manage risks? 7 1.4 Introduction to derivatives: contracts and applications 8 1.4.1 Forward contracts 9 1.4.2 Futures contracts 10 1.4.3 Swaps 12 1.4.4 Options 12 1.5 Applications and uses of financial derivatives 13 1.5.1 Risk management 13 1.5.2 Speculators 14 1.5.3 Arbitrageurs 14 1.5.4 The price discovery role of derivatives markets 15 1.5.5 Hedging and basis risk 16 1.5.6 Theoretical models of futures prices: the cost-of-carry model 18 1.6 The organisation of this book 20 Appendix 1 .A: derivation of minimum variance hedge ratio 23 Chapter 2: Introduction to Shipping Markets 24 2.1 Introduction 24 2.2 The world shipping industry 24 2.3 Market segmentation in the shipping industry 28 2.3.1 The container shipping market 30 2.3.2 The dry-bulk market 31 2.3.3 The tanker market 34 vi Contents 2.4 Shipping freight contracts 35 2.4.1 Voyage charter contracts 37 2.4.2 Contracts of affreightment 39 2.4.3 Trip-charter contracts 40 2.4.4 Time-charter contracts 41 2.4.5 Bare-boat or demise charter contracts 41 2.5 Definition and structure of costs in shipping 42 2.5.1 Capital costs 42 2.5.2 Operating costs 43 2.5.3 Voyage costs 43 2.5.4 Cargo-handling costs 44 2.6 Spot freight-fate formation 44 2.7 Time-charter rate formation 48 2.7.1 Time-charter equivalent of spot rates (TCE) 51 2.8 Seasonal behaviour of freight rates 52 2.9 The market for ships 55 2.9.1 Factors determining ship prices 55 2.9.2 The newbuilding market 56 2.9.3 The second-hand market 58 2.9.4 The scrap or demolition market 60 2.10 Summary and conclusions 63 Chapter 3: Statistical Tools for Risk Analysis and Modelling 65 3.1 Introduction 65 3.2 Data sources and data-collection methods 65 3.3 Descriptive statistics and moments of a variable 67 3.3.1 Measures of central tendency (location) 67 3.3.2 Measures of dispersion 69 3.3.3 The range 69 3.3.4 Variance and standard deviation 70 3.3.5 Coefficient of skewness 73 3.3.6 Coefficient of kurtosis 74 3.3.7 Coefficient of variation 75 3.3.8 Covariance and correlation 77 3.3.9 Comparison of risk across different vessel size and contracts 78 3.4 Time-varying volatility models 80 3.4.1 Rolling-window or moving-average variance 82 3.4.2 Exponentially weighted average variance (EWAV) 83 3.4.3 Realised volatility models 84 Contents vii 3.5 ARCH and GARCH models 85 3.5.1 The theory of ARCH models 85 3.5.1.1 GARCH models 86 3.5.2 Asymmetric GARCH models 88 3.5.3 GJR threshold GARCH model 90 3.5.4 Exponential GARCH model 90 3.5.5 Markov regime-switching GARCH models 94 3.5.6 The term structure of forward-curve and freight-rate volatility 97 3.5.7 Stochastic volatility models 99 3.5.8 Multivariate GARCH models 100 3.6 Forecasting volatility 102 3.6.1 Historical volatility forecast 102 3.6.2 Exponentially weighted average volatility (RiskMetrics) 103 3.6.3 GARCH models 103 3.7 Summary and conclusions 106 Chapter 4: Freight Market Information 107 4.1 Introduction 107 4.2 Baltic Exchange freight-market information 108 4.2.1 Baltic Capesize Index (BCI) 108 4.2.2 Baltic Panamax Index (BPI) 110 4.2.3 Baltic Supramax Index (BSI) 111 4.2.4 Baltic Handysize Index (BHSI) 111 4.2.5 Baltic Dry Index (BDI) 112 4.2.6 Baltic Clean Tanker Index (BCTI) 113 4.2.7 Baltic Dirty Tanker Index (BDTI) 115 4.2.8 Other indices 117 4.3 Calculation of the Baltic Indices and the role of the panellists 118 4.3.1 Route selection and route changes 120 4.3.2 Calculation of the Baltic Indices 120 4.4 The freight-futures market - historical developments 121 4.5 Summary and conclusions 123 Chapter 5: Forward Freight Agreements 125 5.1 Introduction 125 5.2 What is a forward freight agreement (FFA)? 125 5.2.1 Volume by sector and trade 127 viii Contents 5.3 How are forward freight agreements traded? 131 5.3.1 Trading FFAs in the OTC market 133 5.3.2 Contract documentation in the OTC market 134 5.3.2.1 The FFABA contract 135 5.3.2.2 ISDA® Master Agreement and Schedule 137 5.3.3 Credit risk and clearing 137 5.3.3.1 How clearing houses operate 138 5.3.3.2 Margining and marking to market 141 5.3.3.3 A marking-to-market example 143 5.3.4 Trading via a 'hybrid' exchange 145 5.4 Hedging using forward freight agreements 147 5.4.1 Hedging trip-charter freight-rate risk 148 5.4.2 Hedging using voyage FFAs 149 5.4.3 Time-charter hedge 152 5.4.4 Tanker hedge 157 5.4.5 Hedge-ratio calculation for tanker FFAs 157 5.5 Issues to consider when using FFAs for hedging 158 5.5.1 Settlement risk 158 5.5.2 Basis risk 160 5.6 Uses of forward freight agreements 164 5.7 Price discovery and forward curves 166 5.7.1 Baltic Forward Assessments (BFA) 169 5.8 Summary and conclusions 173 Appendix 5.A: FFABA 2007® Forward Freight Agreement contract 174 Chapter 6: Technical Analysis and Freight Trading Strategies 181 6.1 Introduction 181 6.2 Technical analysis 181 6.2.1 Chart analysis 182 6.3 Technical trading rules 186 6.4 Moving averages (MA) 186 6.4.1 Moving average crossover trading rule 186 6.4.2 Stochastic oscillators 18? 6.5 Filter rules 192 6.5.1 Moving average envelopes 193 6.5.2 Bollinger Bands 194 6.6 The momentum trading model 197 6.7 Spread trading in FFA markets 199 6.7.1 Tanker spread trading 201 6.7.2 Dry-bulk spread trading 203 Contents ix 6.8 Time-charter and implied forward rates 207 6.8.1 The relative value trading rule 211 6.9 Technical trading rules and shipping investment 211 6.10 Summary and conclusions 215 Chapter 7: Options on Freight Rates 217 7.1 Introduction 217 7.2 A primer on options 217 7.3 Properties of option prices 222 7.3.1 Boundary conditions for European call prices 222 7.3.2 Boundary conditions for European put prices 224 7.3.3 Put-call parity 224 7.3.4 Factors affecting the value of call and put options 225 7.4 Practicalities of trading options in the freight market 226 7.5 Risk-management strategies using options 227 7.5.1 An example of hedging using options 231 7.5.2 Hedging using a collar 232 7.5.2.1 Constructing a zero-cost collar in the dry-bulk market 234 7.6 Option-trading strategies 236 7.6.1 Bull spreads 236 7.6.2 Bear spreads 240 7.6.3 Ratio spreads 241 7.6.4 Box spread 243 7.6.5 Straddle combinations 244 7.6.6 Strangle combinations 245 7.6.7 Strips and straps 247 7.6.8 Butterfly spreads 248 7.7 Summary and conclusions 249 Appendix 7.A: FFABA 2007® Freight Options Contract 250 Chapter 8: Pricing and Risk Management of Option Positions 258 8.1 Introduction 258 8.2 Pricing freight options 258 8.2.1 Which approach is better for pricing freight options? 259 8.2.2 The Black-Scholes-Merton (BSM) model (1973) 261 8.2.3 The Black Model (1976) 263 x Contents 8.2.4 The Turnbull and Wakeman Approximation (1991) 264 8.2.5 Levy (1997) and Haug et al. (2003) Discrete Asian Approximation 265 8.2.6 Curran's Approximation 266 8.2.7 Applications for freight markets 267 8.2.8 An option-pricing example 269 8.3 Asian options with volatility term structure 271 8.4 Implied volatility 273 8.5 Pricing Asian options using Monte Carlo simulation 276 8.6 Risk management of option positions 281 8.7 Hedging a short-call position: an example 282 8.8 Option-price sensitivities: 'Greeks' 283 8.9 Delta (A) 284 8.9.1 Delta hedging 286 8.9.2 Delta hedging of Asian options 290 8.10 Gamma (r) 292 8.10.1 Gamma-neutral strategies 294 8.11 Theta(0) 295 8.11.1 The relationship between theta, delta and gamma 297 8.12 Vega (A) 298 8.13 Rho(P) 299 8.13.1 Interpretation of Greek parameters: reading the Greeks 300 8.14 Dynamic hedging in practice 300 8.14.1 Greeks and trading strategies 302 8.15 Summary and conclusions 302 Chapter 9: Value-at-Risk in Shipping and Freight Risk Management 303 9.1 Introduction 303 9.2 Simple VaR estimation 305 9.2.1 VaR of multi-asset portfolios 310 9.3 VaR estimation methodologies 312 9.3.1 Parametric VaR estimation 312 9.3.1.1 The sample variance and covariance method 313 9.3.1.2 The exponential weighted average variance and RiskMetrics method 313 Contents xi 9.3.1.3 GARCH Models and VaR estimation 313 9.3.1.4 Monte Carlo simulation and VaR estimation • 314 9.3.1.5 Recent advances in parametric VaR models 317 9.3.2 Nonparametric VaR estimation methods 319 9.3.2.1 Historical simulation 319 9.3.2.2 The bootstrap method of estimating VaR 321 9.3.2.3 The quantile regression method 322 9.4 VaR for non-linear instruments 322 9.4.1 Mapping VaR for options 323 9.4.2 Delta approximation 325 9.4.3 Delta-gamma approximation 325 9.5 Principal component analysis and VaR estimation 328 9.6 Backtesting and stresstesting of VaR models 333 9.7 Summary and conclusions 335 Appendix 9.A: Principal component analysis 336 Chapter 10: Bunker Risk Analysis and Risk Management 338 10.1 Introduction 338 10.2 The world bunker market 339 10.3 Bunker-price risk in shipping operations 341 10.4 Hedging bunker risk using OTC instruments 343 10.5 Hedging bunker prices using forward contracts 343 10.5.1 Long hedge using forward bunker contract 343 10.5.2 Short hedge using forward bunker contract 344 10.6 Bunker swap contracts 346 10.6.1 Plain vanilla bunker swap 347 10.7 Exotic bunker swaps 350 10.7.1 Differential swap 350 10.7.2 Extendable swap 351 10.7.3 Forward bunker swap 352 10.7.4 Participation swap 353 10.7.5 Double-up swap 354 10.7.6 Variable volume
Load more

Recommended publications
  • Up to EUR 3,500,000.00 7% Fixed Rate Bonds Due 6 April 2026 ISIN
    Up to EUR 3,500,000.00 7% Fixed Rate Bonds due 6 April 2026 ISIN IT0005440976 Terms and Conditions Executed by EPizza S.p.A. 4126-6190-7500.7 This Terms and Conditions are dated 6 April 2021. EPizza S.p.A., a company limited by shares incorporated in Italy as a società per azioni, whose registered office is at Piazza Castello n. 19, 20123 Milan, Italy, enrolled with the companies’ register of Milan-Monza-Brianza- Lodi under No. and fiscal code No. 08950850969, VAT No. 08950850969 (the “Issuer”). *** The issue of up to EUR 3,500,000.00 (three million and five hundred thousand /00) 7% (seven per cent.) fixed rate bonds due 6 April 2026 (the “Bonds”) was authorised by the Board of Directors of the Issuer, by exercising the powers conferred to it by the Articles (as defined below), through a resolution passed on 26 March 2021. The Bonds shall be issued and held subject to and with the benefit of the provisions of this Terms and Conditions. All such provisions shall be binding on the Issuer, the Bondholders (and their successors in title) and all Persons claiming through or under them and shall endure for the benefit of the Bondholders (and their successors in title). The Bondholders (and their successors in title) are deemed to have notice of all the provisions of this Terms and Conditions and the Articles. Copies of each of the Articles and this Terms and Conditions are available for inspection during normal business hours at the registered office for the time being of the Issuer being, as at the date of this Terms and Conditions, at Piazza Castello n.
    [Show full text]
  • (NSE), India, Using Box Spread Arbitrage Strategy
    Gadjah Mada International Journal of Business - September-December, Vol. 15, No. 3, 2013 Gadjah Mada International Journal of Business Vol. 15, No. 3 (September - December 2013): 269 - 285 Efficiency of S&P CNX Nifty Index Option of the National Stock Exchange (NSE), India, using Box Spread Arbitrage Strategy G. P. Girish,a and Nikhil Rastogib a IBS Hyderabad, ICFAI Foundation For Higher Education (IFHE) University, Andhra Pradesh, India b Institute of Management Technology (IMT) Hyderabad, India Abstract: Box spread is a trading strategy in which one simultaneously buys and sells options having the same underlying asset and time to expiration, but different exercise prices. This study examined the effi- ciency of European style S&P CNX Nifty Index options of National Stock Exchange, (NSE) India by making use of high-frequency data on put and call options written on Nifty (Time-stamped transactions data) for the time period between 1st January 2002 and 31st December 2005 using box-spread arbitrage strategy. The advantages of box-spreads include reduced joint hypothesis problem since there is no consideration of pricing model or market equilibrium, no consideration of inter-market non-synchronicity since trading box spreads involve only one market, computational simplicity with less chances of mis- specification error, estimation error and the fact that buying and selling box spreads more or less repli- cates risk-free lending and borrowing. One thousand three hundreds and fifty eight exercisable box- spreads were found for the time period considered of which 78 Box spreads were found to be profit- able after incorporating transaction costs (32 profitable box spreads were identified for the year 2002, 19 in 2003, 14 in 2004 and 13 in 2005) The results of our study suggest that internal option market efficiency has improved over the years for S&P CNX Nifty Index options of NSE India.
    [Show full text]
  • Economic Information Transmissions and Liquidity Between Shipping Markets: New Evidence from Freight Derivatives ⇑ G
    Transportation Research Part E 98 (2017) 82–104 Contents lists available at ScienceDirect Transportation Research Part E journal homepage: www.elsevier.com/locate/tre Economic information transmissions and liquidity between shipping markets: New evidence from freight derivatives ⇑ G. Alexandridis a, S. Sahoo a, I. Visvikis b, a ICMA Centre, Henley Business School, University of Reading, Whiteknights, Reading RG6 6BA, UK b World Maritime University, Fiskehamnsgatan 1, SE-211 18 Malmö, Sweden article info abstract Article history: Economic return and volatility spillovers of derivatives markets on a number of assets have Received 6 July 2016 been extensively examined in the general economics literature. However, there are only a Received in revised form 24 November 2016 limited number of studies that investigate such interactions between freight rates and the Accepted 5 December 2016 freight futures, and no studies that also consider potential linkages with freight options. This study fills this gap by investigating the economic spillovers between time-charter rates, freight futures and freight options prices in the dry-bulk sector of the international JEL Classification: shipping industry. Empirical results indicate the existence of significant information trans- C32 mission in both returns and volatilities between the three related markets, which we attri- G13 G14 bute to varying trading activity and market liquidity. The results also point out that, consistent with theory, the freight futures market informationally leads the freight rate Keywords: market, though surprisingly, freight options lag behind both futures and physical freight Freight derivatives rates. The documented three-way economic interactions between the related markets Options contracts can be used to enhance budget planning and risk management strategies, potentially Price discovery attract more investors, and thus, improve the liquidity of the freight derivatives market.
    [Show full text]
  • 11 Option Payoffs and Option Strategies
    11 Option Payoffs and Option Strategies Answers to Questions and Problems 1. Consider a call option with an exercise price of $80 and a cost of $5. Graph the profits and losses at expira- tion for various stock prices. 73 74 CHAPTER 11 OPTION PAYOFFS AND OPTION STRATEGIES 2. Consider a put option with an exercise price of $80 and a cost of $4. Graph the profits and losses at expiration for various stock prices. ANSWERS TO QUESTIONS AND PROBLEMS 75 3. For the call and put in questions 1 and 2, graph the profits and losses at expiration for a straddle comprising these two options. If the stock price is $80 at expiration, what will be the profit or loss? At what stock price (or prices) will the straddle have a zero profit? With a stock price at $80 at expiration, neither the call nor the put can be exercised. Both expire worthless, giving a total loss of $9. The straddle breaks even (has a zero profit) if the stock price is either $71 or $89. 4. A call option has an exercise price of $70 and is at expiration. The option costs $4, and the underlying stock trades for $75. Assuming a perfect market, how would you respond if the call is an American option? State exactly how you might transact. How does your answer differ if the option is European? With these prices, an arbitrage opportunity exists because the call price does not equal the maximum of zero or the stock price minus the exercise price. To exploit this mispricing, a trader should buy the call and exercise it for a total out-of-pocket cost of $74.
    [Show full text]
  • City Research Online
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by City Research Online City Research Online City, University of London Institutional Repository Citation: Kyriakou, I., Pouliasis, P. K., Papapostolou, N. C. and Andriosopoulos, K. (2017). Freight Derivatives Pricing for Decoupled Mean-Reverting Diffusion and Jumps. Transportation Research Part E: Logistics and Transportation Review, 108, pp. 80-96. doi: 10.1016/j.tre.2017.09.002 This is the accepted version of the paper. This version of the publication may differ from the final published version. Permanent repository link: http://openaccess.city.ac.uk/18168/ Link to published version: http://dx.doi.org/10.1016/j.tre.2017.09.002 Copyright and reuse: City Research Online aims to make research outputs of City, University of London available to a wider audience. Copyright and Moral Rights remain with the author(s) and/or copyright holders. URLs from City Research Online may be freely distributed and linked to. City Research Online: http://openaccess.city.ac.uk/ [email protected] Freight derivatives pricing for decoupled mean-reverting diffusion and jumps Ioannis Kyriakou,∗ Panos K. Pouliasis,† Nikos C. Papapostolou‡and Kostas Andriosopoulos§ Abstract We develop an accurate valuation setup for freight options, featuring an exponential mean- reverting model for the freight rate with distinct reversion scales for its jump and diffusion components. We calibrate to Baltic option prices and analyze the freight rate dynamics. More specifically, we observe that jumps dissipate faster than the diffusive deviations about the equi- librium level. We benchmark against practitioners’ model of choice, i.e., the lognormal model and variants, and find that our approach reduces the pricing error while preserving analytical tractability and computational competence.
    [Show full text]
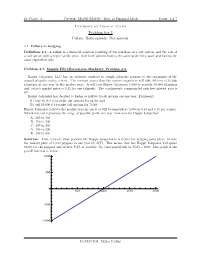
  • Problem Set 2 Collars
    In-Class: 2 Course: M339D/M389D - Intro to Financial Math Page: 1 of 7 University of Texas at Austin Problem Set 2 Collars. Ratio spreads. Box spreads. 2.1. Collars in hedging. Definition 2.1. A collar is a financial position consiting of the purchase of a put option, and the sale of a call option with a higher strike price, with both options having the same underlying asset and having the same expiration date Problem 2.1. Sample FM (Derivatives Markets): Problem #3. Happy Jalape~nos,LLC has an exclusive contract to supply jalape~nopeppers to the organizers of the annual jalape~noeating contest. The contract states that the contest organizers will take delivery of 10,000 jalape~nosin one year at the market price. It will cost Happy Jalape~nos1,000 to provide 10,000 jalape~nos and today's market price is 0.12 for one jalape~no. The continuously compounded risk-free interest rate is 6%. Happy Jalape~noshas decided to hedge as follows (both options are one year, European): (1) buy 10,000 0.12-strike put options for 84.30, and (2) sell 10,000 0.14-strike call options for 74.80. Happy Jalape~nosbelieves the market price in one year will be somewhere between 0.10 and 0.15 per pepper. Which interval represents the range of possible profit one year from now for Happy Jalape~nos? A. 200 to 100 B. 110 to 190 C. 100 to 200 D. 190 to 390 E. 200 to 400 Solution: First, let's see what position the Happy Jalape~nosis in before the hedging takes place.
    [Show full text]
  • Shipping Market Review – May 2021
    SHIPPING MARKET REVIEW – MAY 2021 DISCLAIMER The persons named as the authors of this report hereby certify that: (i) all of the views expressed in the research report accurately reflect the personal views of the authors on the subjects; and (ii) no part of their compensation was, is, or will be, directly or indirectly, related to the specific recommendations or views expressed in the research report. This report has been prepared by Danish Ship Finance A/S (“DSF”). This report is provided to you for information purposes only. Whilst every effort has been taken to make the information contained herein as reliable as possible, DSF does not represent the information as accurate or complete, and it should not be relied upon as such. Any opinions expressed reflect DSF’s judgment at the time this report was prepared and are subject to change without notice. DSF will not be responsible for the consequences of reliance upon any opinion or statement contained in this report. This report is based on information obtained from sources which DSF believes to be reliable, but DSF does not represent or warrant such information’s accuracy, completeness, timeliness, merchantability or fitness for a particular purpose. The information in this report is not intended to predict actual results, and actual results may differ substantially from forecasts and estimates provided in this report. This report may not be reproduced, in whole or in part, without the prior written permission of DSF. To Non-Danish residents: The contents hereof are intended for the use of non-private customers and may not be issued or passed on to any person and/or institution without the prior written consent of DSF.
    [Show full text]
  • Prevailing Ship Financing Methods Applied to Major Dry-Bulk Companies
    UNIVERSITY OF PIRAEUS DEPARTMENT OF MARITIME STUDIES M.Sc. in Maritime Studies SHIPPING FINANCE Prevailing ship financing methods applied to major dry-bulk companies Angeliki Christodoulou Thesis submitted to the department of maritime studies of the University of Piraeus as part of the requirements for the acquisition of the M.Sc. title with specialization in Shipping. Piraeus September 2015 © Copyright Angeliki Christodoulou 2015 All rights reserved “The individual conducting the present thesis bears the full responsibility to determine the right use of the data, a responsibility stipulated according to the following factors: the scope and nature of the use (commercial, non-profitable or educational), the nature of the data processed (part of text, tables, various charts and graphs, images or maps), the percentage and significance of the part used compared to the whole copyright text and the potential consequences of this use in the market or in the general value of the copyright text.” i Committee’s Approval “The present thesis has been unanimously approved by the Three-member Examination Committee appointed by the Special Purpose General Assembly of the Maritime Studies Department of the University of Piraeus in accordance with the Regulations governing the Master in Science in Shipping. The members of the Committee were: Eleftherios Thalassinos (Supervisor) Andreas Merikas Kwnstantinos Liapis The approval of the thesis by the Maritime Studies’ Department of the University of Piraeus does not indicate the acceptance of the writer’s own opinion.” ii ACKNOWLEDGEMENTS I would like to thank sincerely my supervisor, Professor Eleftherios Thalassinos, that without his valuable assistance I would have not been able to conduct this thesis.
    [Show full text]
  • 34-67752; File No
    SECURITIES AND EXCHANGE COMMISSION (Release No. 34-67752; File No. SR-CBOE-2012-043) August 29, 2012 Self-Regulatory Organizations; Chicago Board Options Exchange, Incorporated; Order Approving a Proposed Rule Change Relating to Spread Margin Rules I. Introduction On May 29, 2012, the Chicago Board Options Exchange, Incorporated (“Exchange” or “CBOE”) filed with the Securities and Exchange Commission (“Commission”), pursuant to Section 19(b)(1) of the Securities Exchange Act of 1934 (“Act”)1 and Rule 19b-4 thereunder,2 a proposed rule change to amend CBOE Rule 12.3 to propose universal spread margin rules. The proposed rule change was published for comment in the Federal Register on June 7, 2012.3 The Commission received no comment letters on the proposed rule change. This order approves the proposed rule change. II. Description of the Proposal An option spread is typically characterized by the simultaneous holding of a long and short option of the same type (put or call) where both options involve the same security or instrument, but have different exercise prices and/or expirations. To be eligible for spread margin treatment, the long option may not expire before the short option. These long put/short put or long call/short call spreads are known as two-legged spreads. Since the inception of the Exchange, the margin requirements for two-legged spreads have been specified in CBOE margin rules.4 The margin requirement for a two-legged spread 1 15 U.S.C. 78s(b)(1). 2 17 CFR 240.19b-4. 3 Securities Exchange Act Release No. 67086 (May 31, 2012), 77 FR 33802.
    [Show full text]
  • Revealed Preferences for Energy Efficiency in the Shipping Markets
    LONDON’S GLOBAL UNIVERSITY Revealed preferences for energy efficiency in the shipping markets Prepared for Carbon War Room August 2016 Authors Vishnu Prakash, UCL Energy Institute Dr Tristan Smith, UCL Energy Institute Dr Nishatabbas Rehmatulla, UCL Energy Institute James Mitchell, Carbon War Room Professor Roar Adland, Department of Economics, Norwegian School of Economics (NHH) Contact If you have any queries related to this report, please get in touch. James Mitchell +44 1865 514214 Carbon War Room [email protected] Dr Tristan Smith UCL Energy Institute +44 203 108 5984 [email protected] About UCL Energy Institute UCL Energy Institute delivers world-leading learning, research, and policy support on the challenges of climate change and energy security. Its approach blends expertise from across UCL, to make a truly interdisciplinary contribution to the development of a globally sustainable energy system. The shipping group at UCL Energy Institute consists of researchers and PhD students, involved in a number of on-going projects funded through a mixture of research grants and consultancy vehicles (UMAS). The group undertakes research using models of the shipping system (GloTraM), shipping big data (including satellite Automatic Identification System data), and qualitative and social science analysis of the policy and commercial structure of the shipping system. The shipping group’s research activity is centred on understanding patterns of energy demand in shipping and how this knowledge can be applied to help shipping transition to a low carbon future. The group is world leading on two key areas: using big data to understand trends and drivers of shipping energy demand or emissions and using models to explore what-ifs for future markets and policies.
    [Show full text]
  • Options Trading
    OPTIONS TRADING: THE HIDDEN REALITY RI$K DOCTOR GUIDE TO POSITION ADJUSTMENT AND HEDGING Charles M. Cottle ● OPTIONS: PERCEPTION AND DECEPTION and ● COULDA WOULDA SHOULDA revised and expanded www.RiskDoctor.com www.RiskIllustrated.com Chicago © Charles M. Cottle, 1996-2006 All rights reserved. No part of this publication may be printed, reproduced, stored in a retrieval system, or transmitted, emailed, uploaded in any form or by any means, electronic, mechanical photocopying, recording, or otherwise, without the prior written permission of the publisher. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold with the understanding that neither the author or the publisher is engaged in rendering legal, accounting, or other professional service. If legal advice or other expert assistance is required, the services of a competent professional person should be sought. From a Declaration of Principles jointly adopted by a Committee of the American Bar Association and a Committee of Publishers. Published by RiskDoctor, Inc. Library of Congress Cataloging-in-Publication Data Cottle, Charles M. Adapted from: Options: Perception and Deception Position Dissection, Risk Analysis and Defensive Trading Strategies / Charles M. Cottle p. cm. ISBN 1-55738-907-1 ©1996 1. Options (Finance) 2. Risk Management 1. Title HG6024.A3C68 1996 332.63’228__dc20 96-11870 and Coulda Woulda Shoulda ©2001 Printed in the United States of America ISBN 0-9778691-72 First Edition: January 2006 To Sarah, JoJo, Austin and Mom Thanks again to Scott Snyder, Shelly Brown, Brian Schaer for the OptionVantage Software Graphics, Allan Wolff, Adam Frank, Tharma Rajenthiran, Ravindra Ramlakhan, Victor Brancale, Rudi Prenzlin, Roger Kilgore, PJ Scardino, Morgan Parker, Carl Knox and Sarah Williams the angel who revived the Appendix and Chapter 10.
    [Show full text]
  • Strike Price
    Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways Applying Principles of Quantitative Finance to Modeling Derivatives of Non-Linear Payoffs Christopher Ting http://www.mysmu.edu/faculty/christophert/ Christopher Ting k: [email protected] T: 6828 0364 ÿ: LKCSB 5036 October 3, 2017 Christopher Ting QF 101 October 3, 2017 1/46 Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways Table of Contents 1 Introduction 2 Options’ Basics 3 Put-Call Parity 4 Overall Shape of Call 5 Box Spread Parity 6 Takeaways Christopher Ting QF 101 October 3, 2017 2/46 Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways Code of King Hammurabi, 1792 to 1750 BC Picture source: Code of Hammurabi Picture source: The Louvre Christopher Ting QF 101 October 3, 2017 3/46 Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways King Hammurabi’s 48-th Code If any one owe a debt for a loan, and a storm prostrates the grain, or the harvest fail, or the grain does not grow for lack of water; in that year he need not give his creditor any grain, he washes his debt-tablet in water and pays no rent for this year. From the perspective of a creditor, ¡ Underlying asset: grain ¡ Expiration: at harvest ¡ Delivery mode: physical ¡ Condition: if not (a storm prostrates the grain, or the harvest fail, or the grain does not grow for lack of water) Christopher Ting QF 101 October 3, 2017 4/46 Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways Discussion ¡ Is the 48-th Code fair to the farmer? ¡ Is the 48-th Code fair to the creditor? ¡ Why should the creditor lend to the farmer in the first place? Christopher Ting QF 101 October 3, 2017 5/46 Introduction Options’ Basics Put-Call Parity Overall Shape of Call Box Spread Parity Takeaways Publicly Listed Options ¡ Options used to be, and still is traded OTC.
    [Show full text]