SYLLABUS of BASIC EDUCATION 2021 Modern Actuarial Statistics-I – Exam MAS-I
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

STATISTICS APPLIED to PSYCHOLOGY I – Code 800146 Academic Year 2020-21
STATISTICS APPLIED TO PSYCHOLOGY I – Code 800146 Academic Year 2020-21 COURSE INFORMATION Undergraduate Studies: 0812 – Bachelor’s degree in Psychology (Studies Plan 2009-10) Type: Basic (compulsory) ECTS: 6.0 Module: Basic training Area: Statistics Year: First Semester: 1 LECTURER INFORMATION Name: Rocío Alcalá Quintana, PhD Mail: [email protected] Office number: 2121-O Office hours (fall semester): Tuesdays and Thursdays, from 15.30 to 18.00. SYNOPSIS COMPETENCIES General competencies GC6: Know and understand research methods and data analysis techniques. Transversal competencies TC1: Analysis and synthesis. TC2: Preparation and defence of properly reasoned arguments. TC3: Problem solving and decision making in Psychology. TC5: Looking for information and data interpretation on social, scientific and ethical topics related to the field of Psychology. TC6: Team work and collaboration with other professionals TC7: Critical thinking and self- analysis. TC8: Learning how to learn, skills for life-long learning. Specific competencies SC17: Be able to measure and obtain relevant data for the evaluation of interventions. SC18: Know how to analyse and interpret results of evaluations. SC19: Know how to appropriately and accurately provide feedback to recipients. TEACHING ACTIVITIES TEACHING ACTIVITIES Hours % of total Attendance credits Theory classes 45 30 % 100% Practical sessions 15 10 % 100% Students' work 82.5 55 % 0% Assessment 7.5 5 % 100% BRIEF DESCRIPTION: Basic concepts of measurement and types of variables. Introduction to Statistics. Data summarization and visualization. Measures of central tendency, variability, and skewness. Measures of association. Introduction to probability theory. Probability distributions of some continuous and discrete random variables. Sampling. PRE-REQUISITES Basic proficiency in secondary school maths is required to follow the course adequately. -

Math 234: Course Syllabus – Spring 2013
Math 234: Course Syllabus – Spring 2013 Course logistics: Time and Location: Tuesday & Thursday 3:30pm – 4:45pm, 251 Mercer St., CIWW 517 Instructor: Michael O’Neil Email: [email protected] Phone: 212-992-5874 Office: Room 1105A, Warren Weaver Hall Office hours: Thursday 11:00am – 1:00pm Course website: See NYU Classes Recitation time: Friday 2:00pm – 3:15pm, 25 W. 4th St., C-8 Teaching assistant: Alex RoZinov Email: [email protected] Course information: Description: This course is intended as a thorough mathematical introduction to the theory of statistics, intended to be taken after sufficiency in probability is obtained at the level of Math 233: Theory of Probability. Topics covered in this class will include: sampling theory, hypothesis testing, point (parameter) estimation, regression and linear least squares, the bootstrap, tests of significance, likelihood methods, and an intro to Bayesian statistics. The course will mainly focus on analytical approaches, but will contain computational aspects of statistics such as simulation, least squares, tests of significance, etc. Text: Mandatory, homework problems will be assigned from it: Bulmer, Principles of Statistics Suggested references: Rice, Mathematical Statistics and Data Analysis Wasserman, All of Statistics Casella & Berger, Statistical Inference (graduate level) Schaum’s Outline of Statistics Grading: The grade for the course will be determined based on weekly homework assignments, a midterm, and a final exam. The following rubric will be used: Homework 30% Midterm 30% Final 40% The lowest homework grade will be dropped. Homework is due at the beginning of class on the due date; in the interest of fairness, absolutely no late assignments will be accepted. -

IN STATISTICS Under Choice Based Credit System (CBCS)
SYLLABUS FOR B.SC. (HONOURS) IN STATISTICS Under Choice Based Credit System (CBCS) Effective from 2017-2018 The University of Burdwan Burdwan-713104 West Bengal 1 Outlines of Course Structures The main components of this syllabus are as follows: 1. Core Course 2. Elective Course 3. Ability Enhancement Course 1. Core Course (CC) A course, that should compulsorily be studied by a candidate as a core requirement, is termed as a core course. 2. Elective Course 2.1 Discipline Specific Elective (DSE) Course: A course, which may be offered by the main discipline/subject of study, is referred to as Discipline Specific Elective. 2.2 Generic Elective (GE) Course: An elective course, chosen generally from an unrelated discipline/subject of study with intention to seek an exposure, is called a Generic Elective Course. 3. Ability Enhancement Course (AEC) The Ability Enhancement Course may be of two kinds: 3.1 Ability Enhancement Compulsory Course (AECC) 3.2 Skill Enhancement Course (SEC) Details of Courses of B.Sc. (Honours) under CBCS Course Credit Marks 1 Core Course (14 papers) Theory + Theory +Tutorial 14×75= 1050 Practical 14× (5+1)=84 14×(4+2)=84 2 Elective Course (8 Papers) A. DSE 4×(4+2)=24 4×(5+1)=24 4´75= 300 (4 Papers) B. GE 4×(4+2)=24 4×(5+1)=24 4´75= 300 (4 Papers) 3 Ability Enhancement Course A. AECC (2 Papers) AECC1 (ENVS) 4×1=4 4×1=4 100 AECC2 (English/MIL) 2×1=2 2×1=2 50 B. SEC (2 Papers) 2×2=4 2×2=4 2´50= 100 Total Credit : 142 142 Total Marks = 1900 2 Semester wise Course Structures Semester Course Course Name of the Course Pattern -

2010 Amazon 100 Bestsellers in Applied Mathematics November 12, 2010 10:30 AM
2010 Amazon 100 Bestsellers in Applied Mathematics November 12, 2010 10:30 AM. 1. Freakonomics Rev Ed: (and Other Riddles of Modern Life) Steven D. Levitt, Stephen J. Dubner HC? [Kindle] 2. The Calculus Diaries: How Math Can Help You Lose Weight, Win in Vegas, and Survive a Zombie Apocalypse by Jennifer Ouellette 3. How to Measure Anything: Finding the Value of Intangibles in Business by Douglas W. Hubbard 4. The Visual Display of Quantitative Information, 2nd edition by Edward R. Tufte 5. Secrets of Mental Math: The Mathemagician's Guide to Lightning Calculation and Amazing Math Tricks by Arthur Benjamin, Michael Shermer 6. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches by John W. Creswell 7. How to Lie with Statistics by Darrell Huff 8. Secrets of Mental Math: The Mathemagician's Guide to Lightning Calculation and Amazing Math Tricks Michael Shermer [Kindle] 9. Cartoon Guide to Statistics by Larry Gonick, Woollcott Smith 10. Statistics for Dummies by Deborah Rumsey 11. Discovering Statistics Using SPSS (Introducing Statistical Methods) by Andy Field 12. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets by Nassim Nicholas Taleb 13. Freakonomics Rev Ed: (and Other Riddles of Modern Life) Steven D. Levitt, Stephen J. Dubner PB? [Kindle] 14. The Drunkard's Walk: How Randomness Rules Our Lives (Vintage) by Leonard Mlodinow 15. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets by Nassim Nicholas Taleb [Kindle] 16. Envisioning Information by Edward R. Tufte 17. Now You See It: Simple Visualization Techniques for Quantitative Analysis by Stephen Few 18. -

Download Schaum's Outline of Statistics and Econometrics
NEW CUSTOMER? START HERE. Schaum's Outline of Statistics and Econometrics, Second Edition, Dominick Salvatore, Derrick Reagle, McGraw-Hill Education, 2011, 0071755470, 9780071755474, 336 pages. The ideal review for your statistics and econometrics course More than 40 million students have trusted Schaum’s Outlines for their expert knowledge and helpful solved problems. Written by renowned experts in their respective fields, Schaum’s Outlines cover everything from math to science, nursing to language. The main feature for all these books is the solved problems. Step-by-step, authors walk readers through coming up with solutions to exercises in their topic of choice. Clear, concise explanations of all statistics and econometrics concepts Appropriate for the following courses: Statistics and Econometrics, Statistical Methods in Economics, Quantitative Methods in Economics, Mathematical Economics, Micro-Economics, Macro-Economics, Math for Economists, Math for Social Sciences . DOWNLOAD PDF HERE International economics , Dominick Salvatore, Jan 15, 1998, , 766 pages. Posodobljena in vsebinsko razširjena šesta izdaja svetovne uspešnice s področja mednarodnega gospodarstva vključuje mnoga nova poglavja, študije primerov, najnovejše podatke in .... Microeconomics Theory and Applications, Dominick Salvatore, 2003, Business & Economics, 724 pages. "This fully-revised text provides robust coverage of intermediate microeconomics within a global context. Building on the success of previous editions, the text presents a .... Schaum's Outline of Structural Steel Design , Abraham Rokach, 1991, Technology & Engineering, 187 pages. A revision guide for students of structural engineering aiming to provide a succinct description of the key features of structural steel design using LRFD. Among topics .... Statistical estimation of simultaneous economic relationships , Anirudh Lal Nagar, 1959, Business & Economics, 96 pages. -

STATISTICS APPLIED to PSYCHOLOGY I – Code 800146 Academic Year 2018-19
STATISTICS APPLIED TO PSYCHOLOGY I – Code 800146 Academic Year 2018-19 COURSE INFORMATION Undergraduate Studies: 0812 – Bachelor’s degree in Psychology (Studies Plan 2009-10) Type: Basic (compulsory) ECTS: 6.0 Module: Basic training Area: Statistics Year: First Semester: 1 LECTURER INFORMATION Name: Rocío Alcalá Quintana, PhD Mail: [email protected] Office number: 2121-O Office hours (fall semester): Tuesdays and Thursdays, from 15.30 to 18.00. SYNOPSIS COMPETENCIES General competencies GC6: Know and understand research methods and data analysis techniques. Transversal competencies TC1: Analysis and synthesis. TC2: Preparation and defence of properly reasoned arguments. TC3: Problem solving and decision making in Psychology. TC5: Looking for information and data interpretation on social, scientific and ethical topics related to the field of Psychology. TC6: Team work and collaboration with other professionals TC7: Critical thinking and self- analysis. TC8: Learning how to learn, skills for life-long learning. Specific competencies SC17: Be able to measure and obtain relevant data for the evaluation of interventions. SC18: Know how to analyse and interpret results of evaluations. SC19: Know how to appropriately and accurately provide feedback to recipients. TEACHING ACTIVITIES TEACHING ACTIVITIES Hours % of total Attendance credits Theory classes 45 30 % 100% Practical sessions 15 10 % 100% Students' work 82.5 55 % 0% Assessment 7.5 5 % 100% BRIEF DESCRIPTION: Basic concepts of measurement and types of variables. Introduction to Statistics. Data summarization and visualization. Measures of central tendency, variability, and skewness. Measures of association. Introduction to probability theory. Probability distributions of some continuous and discrete random variables. Sampling. PRE-REQUISITES Basic proficiency in secondary school maths is required to follow the course adequately. -

Statistics (Hons.) Syllabus W.E.F. 2008-09.Pdf
UNIVERSITY OF KALYANI SYLLABUS FOR THREE YEARS B.Sc. DEGREE COURSE (HONOURS) IN STATISTICS According to the New Examination Pattern Part – I, Part- II & Part- III WITH EFFECT FROM THE SESSION 2008 - 2009 University of Kalyani Syllabus of Statistics w.e.f. the session 2008-2009 Contents Honours Course Paper Topic Page No. Distribution of Marks and Question Pattern (i & ii) Part-I Paper-I Prob I (H-2) Mathematical Methods I (H-3) Paper-II Descriptive Statistics (H-4) Paper-III Practical (H-4) Part-II Paper- IV Prob II (H-6) Mathematical Methods II (H-7) Paper- V Sampling Distributions (H-8) Estimation and Testing (H-9) Paper-VI Practical (H-9) Part-III Paper- VII Economic Statistics (H-11) Demography (H-12) Indian Statistical System (H-12) Paper- VIII Analysis of Variance & Design of Experiments (H-13) Sampling Techniques (H-14) Paper- IX Sequential Analysis and Non-parametric inference (H-15) Large Sample Methods (H-15) Statistical Quality Control (H-16) Paper- X Practical (H-17) Paper- XI Practical (H-17) University of Kalyani Syllabus of Statistics (Honours) w.e.f. the session 2008-2009 Part - I : (Theo. 150+ Prac. 50) No. of Periods . Marks Gross Net(for course preparation) Paper – I: Prob I (3) 45 6 x 4 x 3 = 72 60 Mathematical Methods I (2) 30 6 x 4 x 2 = 48 40 (Linear Alg.+ Real Ana. I ) Paper- II: Descriptive Statistics (4) 75 6 x 4 x 4 = 96 80 _____ 150 Paper- III (Prac.): Based on Linear Alg. & Descriptive Statistics (2+2 =4) 50 6 x 4 x 4 = 96 80 ____________________________________ ___________ 13 200 6 x 4 x 13 = 312 260 Part – II : (Theo. -

Ebook Download the PSPP Guide (Basic Edition) an Introduction to Statistical Analysis 1St Edition Kindle
THE PSPP GUIDE (BASIC EDITION) AN INTRODUCTION TO STATISTICAL ANALYSIS 1ST EDITION PDF, EPUB, EBOOK Christopher Halter | 9780692313244 | | | | | The PSPP Guide (Basic Edition) An Introduction to Statistical Analysis 1st edition PDF Book Need an account? Relying on the p-value alone can give you a false sense of security. Least squares applied to linear regression is called ordinary least squares method and least squares applied to nonlinear regression is called non-linear least squares. Paired Samples t-Test Window View the output window. Bibcode : Natur.. We could also determine the effect size for an Independent Samples t-Test with the r2 calculation. Christopher Halter. Variable names must be less than 64 characters long. The test results in the graph visually represents the amount of information or variance that can be accounted for within a specific number of factors. These descriptive data points include five highest and lowest values, the percentile points, measures of central tendency, standard deviation, skewness, kurtosis, etc. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general. Output table for reading score by gender Next we will look at the variable entry dialogue window using reading scores as the dependent variable and SES as the fixed factor. Sampling theory is part of the mathematical discipline of probability theory. Often we take sample data to represent some larger population. Main article: Statistical inference. There are also other ways to contact the FSF. Navigate the dialogue box to select the file containing your data. We may have found that the primary home languages are English, Spanish, French, and Cantonese. -

STATISTICS (Revised in 2018)
SEMESTER POST - GRADUATE COURSE IN STATISTICS Department of Statistics, H.N.B.Garhwal Central University, Srinagar (Garhwal) M.A. / M.Sc. course in Statistics is meant for two years spread in four semesters. Each of the theory and practical paper consists of 100 marks. Four theory papers and two practicals will be undertaken in each semester. Eligibility: B.A. /B.Sc. with Mathematics. Preference to those who have Statistics as a subject at B.A. /B.Sc. level. (Revised in 2018) (Effective from the Academic Session 2019-2020) 1 Distribution of different courses and credits in various semesters: First Semester Course Code Title of the Paper Credit ST-101 Real Analysis and Complex Analysis 3 ST-102 Matrices 3 ST-103 Measure Theory and Probability 3 ST-104 Distribution Theory 3 SP-105 Practical I 3 SP-106 Practical II 3 Total 18 Second Semester Course Code Title of the Paper Credit ST-201 Statistical Inference 3 ST-202 Survey Sampling 3 ST-203 Design and Analysis of Experiment 3 ST-204 Linear Algebra 3 SP-205 Practical I 3 SP-206 Practical II 3 Total 18 Third Semester Course Code Title of the Paper Credit ST-301 Multivariate Analysis and Curve Fitting 3 Elective/Optional Any three papers out of the paper 3 X 3= 9 Papers Nos. ST-302 to ST-309 ST-302 Advanced Operations Research I ST-303 Statistical process and Quality control ST-304 Reliability theory ST-305 Research methodology and project work - I 2 ST-306 Statistical decision theory ST-307 Statistical Computing ST-308 Nonparametric and Semiparametric methods ST-309 Linear Models and Regression Analysis SP-310 Practical I 3 SP-311 Practical II 3 Total 18 Fourth Semester Course Code Title of the Paper Credit ST-401 Economic Statistics and Demography 3 Elective/Optional Any three papers out of the paper 3 X 3= 9 Papers Nos. -

Statistics.Pdf
SCHAUM'S OUTLINE OF TheoryandProblemsof STATISTICS This page intentionally left blank SCHAUM'S OUTLINE OF TheoryandProblemsof STATISTICS Fourth Edition . MURRAY R. SPIEGEL, Ph.D. Former Professor and Chairman Mathematics Department, Rensselaer Polytechnic Institute Hartford Graduate Center LARRY J. STEPHENS, Ph.D. Full Professor Mathematics Department University of Nebraska at Omaha . Schaum’s Outline Series McGRAW-HILL New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto Copyright © 2008, 1999, 1988, 1961 by The McGraw-Hill Companies, Inc. All rights reserved. Manufactured in the United States of America. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. 0-07-159446-9 The material in this eBook also appears in the print version of this title: 0-07-148584-8. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. For more information, please contact George Hoare, Special Sales, at [email protected] or (212) 904-4069. -
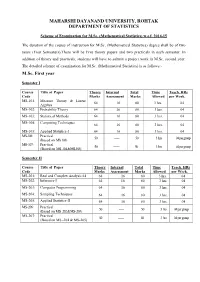
Scheme of Examination for M.Sc. (Mathematical Statistics) Wef 2014-15
MAHARSHI DAYANAND UNIVERSITY, ROHTAK DEPARTMENT OF STATISTICS Scheme of Examination for M.Sc. (Mathematical Statistics) w.e.f. 2014-15 The duration of the course of instruction for M.Sc. (Mathematical Statistics) degree shall be of two years (Four Semesters).There will be Five theory papers and two practicals in each semester. In addition of theory and practicals, students will have to submit a project work in M.Sc. second year. The detailed scheme of examination for M.Sc. (Mathematical Statistics) is as follows:- M.Sc. First year Semester I Course Title of Paper Theory Internal Total Time Teach. HRs Code Marks Assessment Marks Allowed per Week. MS-101: Measure Theory & Linear 64 16 80 3 hrs. 04 Algebra MS-102: Probability Theory 64 16 80 3 hrs. 04 MS-103: Statistical Methods 64 16 80 3 hrs. 04 MS-104: Computing Techniques 64 16 80 3 hrs. 04 MS-105: Applied Statistics-I 64 16 80 3 hrs. 04 MS-106: Practical 50 ------ 50 3 hrs 04 per group (Based on MS 103) MS- 107 : Practical 50 ------- 50 3 hrs 04 per group (Based on MS -104 & MS-105) Semester II Course Title of Paper Theory Internal Total Time Teach. HRs Code Marks Assessment Marks Allowed per Week. MS-201: Real and Complex Analysis 64 64 16 80 3 hrs. 04 MS-202: Inference-I 64 16 80 3 hrs. 04 MS-203: Computer Programming 64 16 80 3 hrs. 04 MS-204: Sampling Techniques 64 16 80 3 hrs. 04 MS-205: Applied Statistics-II 64 16 80 3 hrs. -

Spring 2017 Econ 3640-002 Probability and Statistical Inference
Spring 2017 Econ 3640-002 Probability and Statistical Inference This course fulfills QB general education requirement. Instructor: Sophie Wu Class meets: T/TH from 12:25 pm to 1:45 pm Classroom: ST 216 Email: [email protected] [email protected] Office hours: T/TH 3:00 pm – 4:20 pm or by appointment through email. Course Overview This course is designated to fulfill the QB general education requirement at the university. It aims to help students obtain a deep understanding of statistical theories and applications in the business world. This course will be divided into three sections. In the first section, we will primarily study the fundamental concept of descriptive statistics. Students are expected to have a clear understanding of how to find the central locations and determine the amount of variation of any set of data. In the second section, we will primarily focus on the probability theory, and how it links to the sampling distribution. In the third section, we will primarily study the statistical inference in the normal distribution, t-distribution, Chi-squared distribution and F distributions, etc. Students are expected to be familiar with the procedures of testing the validity of the hypotheses. By the end of this semester, students are expected to demonstrate qualitative literacy and problem solving abilities. Qualitative literacy includes the following aspects: (1) Interpretation: ECON 3640 teaches how to interpret different types of graphs (for example, pie chart, bar graph, histograms), numerical summaries of data (for example, proportion, mean, median, variance, standard deviation), statistical test results (for example, hypothesis tests about means, proportions).