DOCSLIB.ORG

Collision Attacks on AES-192/256, Crypton-192/256, Mcrypton-96/128, and Anubis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Collision Attacks on AES-192/256, Crypton-192/256, Mcrypton-96/128, and Anubis Hindawi Publishing Corporation Journal of Applied Mathematics Volume 2013, Article ID 713673, 10 pages http://dx.doi.org/10.1155/2013/713673 Research Article Collision Attacks on AES-192/256, Crypton-192/256, mCrypton-96/128, and Anubis Jinkeon Kang,1 Kitae Jeong,1 Jaechul Sung,2 Seokhie Hong,1 and Kyungho Lee1 1 Center for Information Security Technologies (CIST), Korea University, Anam-dong, Seongbuk-gu, Seoul 136-713, Republic of Korea 2 Department of Mathematics, University of Seoul, Jeonnong-dong, Dongdaemun-gu, Seoul 130-743, Republic of Korea Correspondence should be addressed to Kyungho Lee; [email protected] Received 19 July 2013; Accepted 22 August 2013 Academic Editor: Jongsung Kim Copyright © 2013 Jinkeon Kang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. At AES’00, a collision attack on 7-round reduced AES was proposed. In this paper, we apply this idea to seven SPN block ciphers, AES-192/256, Crypton-192/256, mCrypton-96/128, and Anubis. Applying our attacks on AES-192/256, we improve the attack result based on meet-in-the-middle attack (AES-192) and the attack result proposed in AES’00 (AES-256), respectively. Our attack result on Anubis is superior to known cryptanalytic result on it. In the cases of Crypton-192/256 and mCrypton-96/128, our attacks are applicable to 8-round reduced versions. The attack results on mCrypton-96/128 are more practical than known cryptanalytic results on them. 1. Introduction attack results on them. Rijndael was announced as the Advanced Encryption Standard (AES) in 2001. After DES, it Recently, meet-in-the-middle attack has received attention. isoneofthemostwidelyusedandanalyzedciphersinthe The attack procedure of meet-in-the-middle attack can be world. AES is a 128-bit block cipher and accepts key sizes of summarized as follows. Let M be the message space and K 128, 192,and256 bits. These versions of AES are called AES- thekeyspace.Supposethat and : M × K → M are 128/192/256 and the number of rounds for these versions two block ciphers and let = ∘. In this attack, an is 10, 12,and14, respectively. Our attacks on AES-192/256 69.2 attacker tries to deduce from a given plaintext/ciphertext require a computational complexity of 2 encryptions with −1 32 74 pair =() by trying to solve () = ().In 2 chosen plaintexts and 2 memory bytes, respectively. somecases,theequationisnottestedforallthebitsof Though our attacks on them are not applicable to the full the intermediate encryption value, but rather for only some AES-192/256, these are superior to the attack results of [1] of them. So far, many meet-in-the-middle attack results on (AES-192)and[3](AES-256), respectively. block cipher have been proposed [1, 2]. On the other hand, Crypton is a 128-bit block cipher submitted as a candidate Gilbert and Minier proposed a collision attack on 7-round for the AES proposal of NIST. This algorithm has a 12-round of AES in [3]. This attack is a type of meet-in-the middle SPN structure with 128/192/256-bit secret keys. According attack and exploits a 4-round distinguisher. In general, block to the length of the secret keys, we call them Crypton- cipher is completely deterministic, that is, if it is run again 128/192/256, respectively. Our attack is applicable to 8-round with the exact same input values, identical output values will reduced Crypton-192/256. To our knowledge, truncated dif- be produced. Similarly, the different input values result in ferential cryptanalysis on 8-round reduced Crypton-192/256 the different output values. However, it is possible that the has the best results on them, so far [8]. The attacks on an different input values result in the output values of which the 8-round reduced Crypton-192/256 need the computational 161.6 96 specific parts are the same. We call this case a collision. complexity of 2 encryptions with 2 chosen plaintexts 138 In this paper, we apply the main idea of [3]toseven and 2 memory bytes, respectively. Compared to the attack SPN block ciphers, such as AES-192/256 [4], Crypton [5], results of [8], our attacks decrease the data complexity but mCrypton-96/128 [6], and Anubis [7]. Table 1 shows our increase the computational complexity. 2 Journal of Applied Mathematics secret key, the number of rounds is 12 and 14,respectively. 4×4 S00 S01 S02 S03 Each internal state is treated as a byte matrix of size , 8 where each byte represents a value in GF(2 ) (see Figure 1). In round , input/output values and round key are S10 S11 S12 S13 denoted by , ,andRK,respectively(=1,...,12(AES- 0 192)or14 (AES-256)). A whitening key is denoted by RK . The round function of AES-192/256 applies the following S20 S21 S22 S23 four operations to the state matrix: (i) SubBytes (SB): applying the same 8×8invertible S- box 16 timesinparalleloneachbyteofthestate; S30 S31 S32 S33 (ii) ShiftRows (SR): cyclic shift of each row (the th row is shifted by bytes to the left); Figure 1: Internal state of AES-192/256 and Anubis. (iii) MixColumns (MC): multiplication of each column by 8 aconstant4×4matrix over GF(2 ); (iv) AddRoundKey (ARK): XORing the state with a 128- A 64-bit block cipher mCrypton was designed as a bit round key. reduced version of Crypton for a ubiquitous environment. It provides low-resource hardware implementation, which is TheSB,SR,MC,andARKtransformationsareapplied suitable for low-end devices such as RFID tags and wireless to each round except that MC is omitted in the last round. sensor network. Several security aspects related to RFID Besides, before the first round, an extra ARK is applied, tags and wireless sensor network have already been studied. which we call a whitening key step. For the more detailed mCrypton has 12 rounds and supports the 64/96/128-bit descriptions of AES-192/256, we refer to [4]. We omit the key secret keys. Our attack is applicable to mCrypton-96/128. schedules of them, as they do not affect our attacks. 81.6 We require the computational complexity of 2 encryptions 48 65 with 2 chosen plaintexts and 2 memory bytes. However, 2.2. Finding a 4-Round Distinguisher of AES. In our attack this is not the best result on them, since related-key impossi- on AES, we use a 4-rounddistinguisherofround2∼5. We 2 ble differential cryptanalysis on 9-round reduced mCrypton- consider an input value of round 2 in AES which is 96/128 was proposed in [9]. However, considering the attack constructed as follows: assumption of a related-key attack, our attacks are more 2 2 2 2 (i) ( , , , ):four8-bit variables; practical than it. 00 10 20 30 2 Anubis is a block cipher submitted to the NESSIE project (ii) :afixed8-bit constant (0≤≤3,1≤≤3). 128 and operates on data blocks of bits, accepting keys of 2 length 32 bits ( = 4,...,10).ItisaRijndaelvariant By using ,wecanconstructthefollowingequationson 3 ( = 0,...,3) that uses involutions for the various operations. Our attack .Here, means the entry of the coefficient (=0,...,3) is applicable to Anubis where the length of the secret key is matrix of MC : longer than 192 bits. We need the computational complexity 3 2 2 2 161.6 96 138 0 =0 ∘ SB [00]⊕1 ∘ SB [11]⊕2 ∘ SB [22] of 2 encryptions with 2 chosen plaintexts and 2 memory bytes. This result is superior to known cryptanalytic 2 2 ⊕3 ∘ SB [33]⊕RK0, results on this algorithm. The rest of this paper is organized as follows. In Section 2, 3 2 2 2 1 =0 ∘ SB [01]⊕1 ∘ SB [12]⊕2 ∘ SB [23] weproposecollisionattacksonAES-192/256.Collision attacks on Crypton-192/256 and mCrypton-96/128 are intro- 2 2 ⊕3 ∘ SB [30]⊕RK1, duced in Section 3.InSection 4,wepresentacollisionattack (1) on Anubis. In each section, we start with a brief description 3 2 2 2 =0 ∘ SB [ ]⊕1 ∘ SB [ ]⊕2 ∘ SB [ ] of the block cipher concerned. Finally, we give our conclusion 2 02 13 20 in Section 5. 2 2 ⊕3 ∘ SB [31]⊕RK2, 3 2 2 2 2. Collision Attacks on 7-Round Reduced 3 =0 ∘ SB [03]⊕1 ∘ SB [10]⊕2 ∘ SB [21] AES-192/256 2 2 ⊕3 ∘ SB [32]⊕RK3. First, we briefly present AES-192/256.Andthenweintroduce 3 3 3 3 collision attacks on AES-192/256.Notethattheattackproce- Note that each 0, 1, 2,and3 depends on only one 192 256 2 2 2 2 dure on AES- isthesameasthatonAES- .Thus,forthe 8-bit variable and one 8-bit round key: (00, RK0), (30, RK1), 192 256 2 2 2 2 simplicity of notations, we just call them AES- / AES. (20, RK2),and(10, RK3). Applying the above procedure repeatedly, as shown in (2), 5 2.1. AES-192/256. AES-192/256 are 128-bit block ciphers wecanobtainanequationonaninputvalue00 of round 5 by 192 256 2 2 2 2 with / -bit secret keys. According to the length of the using . Here, bold characters indicate (10,20,30) Journal of Applied Mathematics 3 5 2 2 2 2 2 00 =00 ∘ SB [00 ∘ SB (00 ∘ SB [00]⊕01 ∘ SB [11]⊕02 ∘ SB [22]⊕03 ∘ SB [33]⊕RK00) 2 2 2 2 2 ⊕01 ∘ SB (10 ∘ SB [01]⊕11 ∘ SB [12]⊕12 ∘ SB [23]⊕13 ∘ SB [I30]⊕RK11) 2 2 2 2 2 ⊕02 ∘ SB (20 ∘ SB [02]⊕21 ∘ SB [13]⊕22 ∘ SB [I20]⊕23 ∘ SB [31]⊕RK22) 2 2 2 2 2 3 ⊕03 ∘ SB (30 ∘ SB [03]⊕31 ∘ SB [I10]⊕32 ∘ SB [21]⊕33 ∘ SB [32]⊕RK33)⊕RK00] 2 2 2 2 2 ⊕01 ∘ SB [10 ∘ SB (00 ∘ SB [01]⊕01 ∘ SB [02]⊕2 ∘ SB [23]⊕03 ∘ SB [I30]⊕RK01) 2 2 2 2 2 ⊕11 ∘ SB (10 ∘ SB [02]⊕11 ∘ SB [13]⊕12 ∘ SB [I20]⊕13 ∘ SB [31]⊕RK12) 2 2 2 2 2 ⊕12 ∘ SB (20 ∘ SB [03]⊕21 ∘ SB [I10]⊕22 ∘ SB [21]⊕23 ∘ SB [32]⊕RK23) 2 2 2 2 2 3 ⊕13 ∘ SB (30 ∘ SB [ ]⊕31 ∘ SB [ ]⊕32 ∘ SB [ ]⊕33 ∘ SB [ ]⊕RK )⊕RK ] 00 11 22 33 30 11 (2) 2 2 2 2 2 ⊕02 ∘ SB [20 ∘ SB (00 ∘ SB [02]⊕01 ∘ SB [13]⊕02 ∘ SB [I20]⊕03 ∘ SB [31]⊕RK02) 2 2 2 2 2 ⊕21 ∘ SB (10 ∘ SB [03]⊕11 ∘ SB [I10]⊕12 ∘ SB [21]⊕13 ∘ SB [32]⊕RK13) 2 2 2 2 2 ⊕22 ∘ SB (20 ∘ SB [00]⊕21 ∘ SB [11]⊕22 ∘ SB [22]⊕23 ∘ SB [33]⊕RK20) 2 2 2 2 2 3 ⊕23 ∘ SB (30 ∘ SB [01]⊕31 ∘ SB [12]⊕32 ∘ SB [23]⊕33 ∘ SB [I30]⊕RK31)⊕RK22] 2 2 2 2 2 ⊕03 ∘ SB [30 ∘ SB (00 ∘ SB [03]⊕01 ∘ SB [I10]⊕02 ∘ SB [21]⊕03 ∘ SB [32]⊕RK03) 2 2 2 2 2 ⊕31 ∘ SB (10 ∘ SB [00]⊕11 ∘ SB [11]⊕12 ∘ SB [22]⊕13 ∘ SB [33]⊕RK10) 2 2 2 2 2 ⊕32 ∘ SB (20 ∘ SB [01]⊕21 ∘ SB [12]⊕22 ∘ SB [23]⊕23 ∘ SB [I30]⊕RK21) 2 2 2 2 2 3 4 ⊕33 ∘ SB (30 ∘ SB [02]⊕31 ∘ SB [13]⊕32 ∘ SB [I20]⊕33 ∘ SB [31]⊕RK32)⊕RK33]⊕RK00.
Load more

Recommended publications
  • Optimization of Core Components of Block Ciphers Baptiste Lambin
    Optimization of core components of block ciphers Baptiste Lambin To cite this version: Baptiste Lambin. Optimization of core components of block ciphers. Cryptography and Security [cs.CR]. Université Rennes 1, 2019. English. NNT : 2019REN1S036. tel-02380098 HAL Id: tel-02380098 https://tel.archives-ouvertes.fr/tel-02380098 Submitted on 26 Nov 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE DE DOCTORAT DE L’UNIVERSITE DE RENNES 1 COMUE UNIVERSITE BRETAGNE LOIRE Ecole Doctorale N°601 Mathématique et Sciences et Technologies de l’Information et de la Communication Spécialité : Informatique Par Baptiste LAMBIN Optimization of Core Components of Block Ciphers Thèse présentée et soutenue à RENNES, le 22/10/2019 Unité de recherche : IRISA Rapporteurs avant soutenance : Marine Minier, Professeur, LORIA, Université de Lorraine Jacques Patarin, Professeur, PRiSM, Université de Versailles Composition du jury : Examinateurs : Marine Minier, Professeur, LORIA, Université de Lorraine Jacques Patarin, Professeur, PRiSM, Université de Versailles Jean-Louis Lanet, INRIA Rennes Virginie Lallemand, Chargée de Recherche, LORIA, CNRS Jérémy Jean, ANSSI Dir. de thèse : Pierre-Alain Fouque, IRISA, Université de Rennes 1 Co-dir. de thèse : Patrick Derbez, IRISA, Université de Rennes 1 Remerciements Je tiens à remercier en premier lieu mes directeurs de thèse, Pierre-Alain et Patrick.
    [Show full text]
  • How Far Can We Go Beyond Linear Cryptanalysis?
    How Far Can We Go Beyond Linear Cryptanalysis? Thomas Baign`eres, Pascal Junod, and Serge Vaudenay EPFL http://lasecwww.epfl.ch Abstract. Several generalizations of linear cryptanalysis have been pro- posed in the past, as well as very similar attacks in a statistical point of view. In this paper, we de¯ne a rigorous general statistical framework which allows to interpret most of these attacks in a simple and uni¯ed way. Then, we explicitely construct optimal distinguishers, we evaluate their performance, and we prove that a block cipher immune to classical linear cryptanalysis possesses some resistance to a wide class of general- ized versions, but not all. Finally, we derive tools which are necessary to set up more elaborate extensions of linear cryptanalysis, and to general- ize the notions of bias, characteristic, and piling-up lemma. Keywords: Block ciphers, linear cryptanalysis, statistical cryptanalysis. 1 A Decade of Linear Cryptanalysis Linear cryptanalysis is a known-plaintext attack proposed in 1993 by Matsui [21, 22] to break DES [26], exploiting speci¯c correlations between the input and the output of a block cipher. Namely, the attack traces the statistical correlation between one bit of information about the plaintext and one bit of information about the ciphertext, both obtained linearly with respect to GF(2)L (where L is the block size of the cipher), by means of probabilistic linear expressions, a concept previously introduced by Tardy-Corfdir and Gilbert [30]. Soon after, several attempts to generalize linear cryptanalysis are published: Kaliski and Robshaw [13] demonstrate how it is possible to combine several in- dependent linear correlations depending on the same key bits.
    [Show full text]
  • Improved Meet-In-The-Middle Attacks on Round-Reduced Crypton-256
    Improved Meet-in-the-Middle Attacks on Round-Reduced Crypton-256 Yonglin Hao Department of Computer Science and Technology, Tsinghua Universtiy, Beijing 100084, China [email protected] Abstract. The meet-in-the-middle (MITM) attack has prove to be efficient in analyzing the AES block cipher. Its efficiency has been increasing with the introduction of various techniques such as differential enumeration, key-dependent sieve, super-box etc. The recent MITM attack given by Li and Jin has successfully mounted to 10-round AES-256. Crypton is an AES-like block cipher. In this paper, we apply the MITM method to the cryptanalysis of Crypton-256. Following Li and Jin's idea, we give the first 6-round dis- tinguisher for Crypton. Based on the distinguisher as well as the properties of Crypton's simple key schedule, we successfully launch MITM attacks on Crypton-256 reduced to 9 and 10 rounds. For 9-round Crypton-256, our MITM attack can recover the 256-bit key with a time complexity 2173:05, a memory complexity 2241:17. For the 10-round version, we give two MITM attacks. The basic attack requires a time complexity 2240:01 and memory complexity 2241:59. The time/memory complexity of the advanced MITM attack on 10-round Crypton is 2245:05=2209:59. Our MITM attacks share the same data complexity 2113 and their error rates are negligible. Keywords: Cryptanalysis, Crypton, MITM, Efficient Differential Enumeration Technique, Key- Dependent Sieve, Super-Box 1 Introduction The SPN-structural block cipher Crypton [1] was proposed by Lim in 1998 as a candidate algorithm for the Advanced Encryption Standard.
    [Show full text]
  • Stochastic Cryptanalysis of Crypton 123
    PublishedStochastic in Fast Software Cryptanalysis Encryption - FSEof 2000 Crypton - LNCS 1978 Marine Minier and Henri Gilbert France T´el´ecom R&D 38-40, rue du G´en´eral Leclerc 92794 Issy les Moulineaux Cedex9-France Tel:+33145294444 Abstract. Crypton is a 12-round blockcipher proposed as an AES can- didate by C.H. Lim in 1998. In this paper, we show how to exploit some statistical deficiencies of the Crypton round function to mount stocha- stic attacks on round-reduced versions of Crypton. Though more efficient than the best differential and linear attacks, our attacks do not endanger the practical security offered by Crypton. 1 Introduction Crypton [Li98] is a 12-round blockcipher which was submitted by C.H. Lim as one of the 15 candidates at the first Advanced Encryption Standard conference in August 1998. Crypton offers several interesting features. The encryption and decryption processes are strictly identical up to the key schedule (a quite re- markable property given the substitution/permutation structure of the cipher). Crypton is highly parallelizable and flexible, and thus well suited for efficient im- plementation on nearly any hardware or software platform. Moreover, Crypton provides some provable resistance against linear and differential cryptanalysis. The main cryptanalytic results obtained on Crypton so far are the analysis of the best differential and linear attacks by the algorithm designer [Li98], a transposition of the square attack to the 6-round Crypton by C. D’Halluin et al. [Hal99], the discovery of some weak keys by Vaudenay [Ba99], and statistical observations contained in an annex of [Ba99].
    [Show full text]
  • Security Systems Architecture on MAC Layer for with Reconfigurable A
    A Software-Radio Platform with Reconfigurable Architecture on MAC Layer for Security Systems por Ignacio Algredo Badillo Tesis sometida como requisito parcial para obtener el grado de DOCTORADO EN CIENCIAS EN LA ESPECIALIDAD DE CIENCIAS COMPUTACIONALES en el Instituto Nacional de Astrof´ısica, Optica´ y Electronica´ Diciembre 2008 Tonantzintla, Puebla Supervisada por: Dra. Claudia Feregrino Uribe, INAOE Dr. Rene´ Armando Cumplido Parra, INAOE °c INAOE 2008 El autor otorga al INAOE el permiso de reproducir y distribuir copias en su totalidad o en partes de esta tesis A Software-Radio Platform with Recon¯gurable Architecture on MAC Layer for Security Systems Ignacio ALGREDO-BADILLO December, 2008 ii Abstract The development, analysis and evaluation of architectures of high perfor- mance, as well as new methodologies of design hardware are useful tools in the area of security systems based on cryptography, where recently it is required flexibility to change di®erent functionalities. It is important to highlight two key points, on the one hand, the cryptographic algorithms utilize com- plex and iterative processes with many operations, and their application in communications networks causes a decreased speed of the data transmission. On the other hand, there is a great amount of communications networks, which establish standards or security architectures based on communication protocols. These last ones have functionalities that are independent of the algorithm, originating several possible combinations between di®erent types networks, protocols and algorithms. So, the flexibility is an important cha- racteristic because an ideal device of digital communications must be con- nected and establish interchange of data in any type of network.
    [Show full text]
  • AES); Cryptography; Cryptanaly- the Candidates
    Volume 104, Number 5, September–October 1999 Journal of Research of the National Institute of Standards and Technology [J. Res. Natl. Inst. Stand. Technol. 104, 435 (1999)] Status Report on the First Round of the Development of the Advanced Encryption Standard Volume 104 Number 5 September–October 1999 James Nechvatal, Elaine Barker, In 1997, the National Institute of Standards (MARS, RC6, Rijndael, Serpent and Donna Dodson, Morris Dworkin, and Technology (NIST) initiated a pro- Twofish) as finalists. The research results James Foti, and Edward Roback cess to select a symmetric-key encryption and rationale for the selection of the fi- algorithm to be used to protect sensitive nalists are documented in this report. National Institute of Standards and (unclassified) Federal information in The five finalists will be the subject of furtherance of NIST’s statutory responsi- further study before the selection of one or Technology, bilities. In 1998, NIST announced the more of these algorithms for inclusion in Gaithersburg, MD 20899-0001 acceptance of 15 candidate algorithms the Advanced Encryption Standard. and requested the assistance of the crypto- Key words: Advanced Encryption graphic research community in analyzing Standard (AES); cryptography; cryptanaly- the candidates. This analysis included an sis; cryptographic algorithms; initial examination of the security and encryption. efficiency characteristics for each al- gorithm. NIST has reviewed the results Accepted: August 11, 1999 of this research and selected five algorithms Available online: http://www.nist.gov/jres Contents 2.4.1.2 Other Architectural Issues ...........442 1. Overview of the Development Process for the Advanced 2.4.1.3 Software .........................442 Encryption Standard and Summary of Round 1 2.4.2 Measured Speed on General Platforms.........442 Evaluations ......................................
    [Show full text]
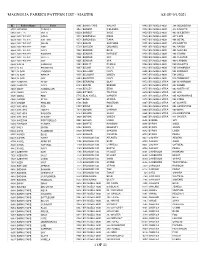
  • Magnolia Fabrics Pattern List - Master As of 9/1/2021
    MAGNOLIA FABRICS PATTERN LIST - MASTER AS OF 9/1/2021 ID Pattern Name Color 9365 BANKS TAPE WALNUT 8842 BRUSSELS 4920 388 MOONBEAM 8207 ABANDO TURKISH 9033 BARBOT ICELANDIC 8853 BRUSSELS 4920 413 ATLANTIC 6883 ABELLA MULTI 10229 BARBOT SAGE 8850 BRUSSELS 4920 463 MULBERRY 9386 ADLER TAPE CORAL 8573 BARONESS ROSE 8839 BRUSSELS 4920 467 CAPE 9339 ADLER TAPE COTTON 8571 BARONESS TIARA 8857 BRUSSELS 4920 468 METAL 9383 ADLER TAPE GRAIN 8974 BASKIN SAPPHIRE 8855 BRUSSELS 4920 479 GROTTO 9385 ADLER TAPE KIWI 5730 BAYLIEH ORLANDO 8851 BRUSSELS 4920 483 RAVEN 9384 ADLER TAPE NAVY 8223 BEADOR BLUE 8832 BRUSSELS 4920 495 GLACIER 9381 ADLER TAPE POWDER 8222 BEADOR HARVEST 8858 BRUSSELS 4920 496 STORM 9382 ADLER TAPE SILVER 8226 BEADOR SKY 8840 BRUSSELS 4920 498 PLASTER 9387 ADLER TAPE SKY 8225 BEADOR SPA 8835 BRUSSELS 4920 499 CARBON 6888 AIRLIA CARNIVAL 8961 BEIRUT PUMICE 8864 BRUSSELS 4920 500 VIOLETTE 10223 ALAS PRISMATIC 8267 BELAIR MULTI 8833 BRUSSELS 4920 505 SHAMROCK 7952 ALGAR LAGOON 7949 BELLAMY NAVY 8856 BRUSSELS 4920 506 EMERALD 7951 ALGAR RIPRAP 8955 BELMONT GREEN 8847 BRUSSELS 4920 508 SHELL 7954 ALGAR SKY 8954 BELMONT NAVY 8848 BRUSSELS 4920 510 TEABERRY 6892 AMORITA BEIGE 5268 BERNERO OLAY 8873 BRUSSELS STRIA 001 MUSHROOM 6895 AMORITA NAVY 5424 BERTIE BREEZE 8874 BRUSSELS STRIA 002 AMBER 8202 ANDY SANDOLLAR 8199 BEXLEY ETNA 8875 BRUSSELS STRIA 003 AMETHYST 8526 ANIKA NAVY 8900 BITTERN TRUFFLE 8870 BRUSSELS STRIA 004 SPA 8525 ANIKA RED 5745 BLACKWELL GARDEN 8871 BRUSSELS STRIA 005 AQUAMARINE 6080 ARBOR PEARL 8227 BLINK SPRING 8872 BRUSSELS
    [Show full text]
  • Advanced Encryption Standard
    ECE297:11Lecture7 Whyanewstandard? 1.Oldstandardinsecureagainstbrute-forceattacks 2.Straightforwardfixesleadtoinefficient implementations AdvancedEncryptionStandard K1 K2 K3 • TripleDES in out 3.Newtrendsinfastsoftwareencryption • useofbasicinstructionsofthemicroprocessor 4.Newwaysofassessingcipherstrength • differentialcryptanalysis • linearcryptanalysis Whyacontest? ExternalformatoftheAESalgorithm • Focustheeffortofcryptographiccommunity plaintextblock Smallnumberofspecialistsintheopenresearch 128bits • Stimulatetheresearchonmethodsofconstructing secureciphers AES key • Avoidbackdoortheories 128,192,256bits 128bits • Speed-uptheacceptanceofthestandard ciphertextblock Rulesofthecontest AESContestEffort Eachteamsubmits June1998 15Candidates Round1 Detailed Justification Tentative fromUSA,Canada,Belgium, Security France,Germany,Norway,UK, Isreal, Softwareefficiency cipher ofdesign results Korea,Japan,Australia,CostaRica description decisions ofcryptanalysis August1999 Round2 5finalcandidates Security Source Mars,RC6, Rijndael,Serpent, Twofish Source Test Hardwareefficiency code code vectors inC inJava October2000 1winner: Rijndael Belgium 1 AEScontest- FirstRound AES:Candidatealgorithms NorthAmerica (8) Europe(4) Asia(2) 15June1998 Deadlineforsubmittingcandidates 21 submissions, Canada: Germany: Korea: 15fulfilledallrequirements CAST-256 Magenta Crypton Deal August1998 1stAESConferenceinVentura,CA Belgium: Japan: USA: Presentationofcandidates Mars Rijndael E2 RC6 March1999 2ndAESConferenceinwRome,Italy Twofish France: Safer+ Australia(1)
    [Show full text]
  • Performance Comparison of the AES Submissions
    Performance Comparison of the AES Submissions Bruce Schneier∗ John Kelseyy Doug Whitingz David Wagnerx Chris Hall{ Niels Ferguson k Version 2.0 February 1, 1999 1 Introduction of the algorithms have different performance char- acteristics for different key lengths. The results are The principal goal guiding the design of any encryp- summarized in Table 1. tion algorithm must be security. In the real world, Nine algorithms|CAST-256, Crypton, DFC, however, performance and implementation cost are E2, Frog, HPC, Mars, RC6, and Serpent|are com- always of concern. Making the assumption that the pletely independent of key length. Two algorithms| major AES candidates are secure (a big assumption, Loki97 and Twofish—encrypt and decrypt indepen- to be sure, but one that is best dealt with in an- dent of key length, but take different times to set up other paper), the most important properties the al- different-size keys1. Twofish takes longer to set up gorithms will be judged on will be the performance a longer key, while Loki97 actually takes less time and cost of implementation. to set up a longer key than it does to set up a In this paper, we will completely ignore secu- shorter key. Four algorithms|DEAL, Magenta, Ri- rity. Instead, we will compare the performance of jndael, and SAFER+|encrypt and decrypt at dif- the leading AES candidates on a variety of common ferent speeds, depending on key length. platforms: 32-bit CPUs, 64-bit CPUs, cheap 8-bit In this paper, we will concentrate on key setup smart-card CPUs, and dedicated hardware.
    [Show full text]
  • Survey and Benchmark of Block Ciphers for Wireless Sensor Networks
    Survey and Benchmark of Block Ciphers for Wireless Sensor Networks Yee Wei Law, Jeroen Doumen and Pieter Hartel Faculty of Electrical Engineering, Mathematics and Computer Science University of Twente, The Netherlands {ywlaw, doumen, pieter}@cs.utwente.nl Abstract. Choosing the most storage- and energy-efficient block cipher specifically for wireless sensor networks (WSNs) is not as straightforward as it seems. To our knowledge so far, there is no systematic evaluation framework for the purpose. In this paper, we have identified the can- didates of block ciphers suitable for WSNs based on existing literature. For evaluating and assessing these candidates, we have devised a system- atic framework that not only considers the security properties but also the storage- and energy-efficency of the candidates. Finally, based on the evaluation results, we have selected the suitable ciphers for WSNs, namely Rijndael for high security and energy efficiency requirements; and MISTY1 for good storage and energy efficiency. 1 Introduction A wireless sensor network (WSN) is a network comprised of a large number of sensors that (1) are physically small, (2) communicate wirelessly among each other, and (3) are deployed without prior knowledge of the network topology. Due to the limitation of their physical size, the sensors tend to have storage space, energy supply and communication bandwidth so limited that every pos- sible means of reducing the usage of these resources is aggressively sought. For example, a sensor typically has 8∼120KB of code memory and 512∼4096 bytes of data memory. The energy supply of a sensor is such that it will be depleted in less than 3 days if operated constantly in active mode [1].
    [Show full text]
  • Cryptanalysis of Symmetric-Key Primitives Based on the AES Block Cipher Jérémy Jean
    Cryptanalysis of Symmetric-Key Primitives Based on the AES Block Cipher Jérémy Jean To cite this version: Jérémy Jean. Cryptanalysis of Symmetric-Key Primitives Based on the AES Block Cipher. Cryp- tography and Security [cs.CR]. Ecole Normale Supérieure de Paris - ENS Paris, 2013. English. tel- 00911049 HAL Id: tel-00911049 https://tel.archives-ouvertes.fr/tel-00911049 Submitted on 28 Nov 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Université Paris Diderot École Normale Supérieure (Paris 7) Équipe Crypto Thèse de doctorat Cryptanalyse de primitives symétriques basées sur le chiffrement AES Spécialité : Informatique présentée et soutenue publiquement le 24 septembre 2013 par Jérémy Jean pour obtenir le grade de Docteur de l’Université Paris Diderot devant le jury composé de Directeur de thèse : Pierre-Alain Fouque (Université de Rennes 1, France) Rapporteurs : Anne Canteaut (INRIA, France) Henri Gilbert (ANSSI, France) Examinateurs : Arnaud Durand (Université Paris Diderot, France) Franck Landelle (DGA, France) Thomas Peyrin (Nanyang Technological University, Singapour) Vincent Rijmen (Katholieke Universiteit Leuven, Belgique) Remerciements Je souhaite remercier toutes les personnes qui ont contribué de près ou de loin à mes trois années de thèse.
    [Show full text]
  • Cryptanalysis of Lightweight Block Ciphers
    Cryptanalysis of Lightweight Block Ciphers Mar´ıaNaya-Plasencia INRIA, France Sibenikˇ 2014 Outline I Introduction I Impossible Differential Attacks I Meet-in-the-middle and improvements I Multiple Differential Attacks I Dedicated attacks (examples) Outline I Introduction I Impossible Differential Attacks I Meet-in-the-middle and improvements I Multiple Differential Attacks Cryptanalysis of Lightweight Block Ciphers Lightweight Block Ciphers I Lightweight Block Ciphers designed for constrained environments, like RFID tags, sensor networks. I Real need ) an enormous amount of proposals in the last years: PRESENT, LED, KATAN/KTANTAN, KLEIN, PRINCE, PRINTcipher, LBLOCK, TWINE, XTEA, mCrypton, Iceberg, HIGHT, Piccolo, SIMON, SPECK, SEA, DESL... 1/30 Lightweight Block Ciphers I Cryptanalysis of lightweight block ciphers: a fundamental task, responsibility of the community. I Importance of cryptanalysis (especially on new proposals): the more a block cipher is analyzed, the more confidence we can have in it... I ...or know which algorithms are not secure to use. 2/30 Lightweight Block Ciphers I Lightweight: more 'risky' design, lower security margin, simpler components. I Often innovative constructions: dedicated attacks I Types of attacks: single-key/related-key, distinguisher/key- recovery, weak-keys, reduced versions. 3/30 Impossible Differential Attacks Classical Differential Attacks [BS'90] Given an input difference between two plaintexts, some output differences occur more often than others. ′ ′ X EK Y ∆X ∆Y ′′ ′′ X EK Y 4/30 Impossible Differential Attacks [K,BBS'98] I Impossible differential attacks use a differential with probability 0. I We can find the impossible differential using the Miss-in-the-middle [BBS'99] technique. I Extend the impossible differential backward and forward ) Active Sboxes transitions give information on the involved key bits.
    [Show full text]