The Effects of More Frequent Observations on Student Achievement Scores a Regression Discontinuity Design Using Evidence from Tennessee
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Revised August 12, 2021 | 85 National Sunshine Series 2021 Week I Special Classes
REVISED AUGUST 12, 2021 | 85 NATIONAL SUNSHINE SERIES 2021 WEEK I SPECIAL CLASSES HUNTER JUMPER FEI 3* WEEK $ 5,000 USHJA National $ Hunter Derby - JR/AM 2,500 Welcome Speed $25,000 Grand Prix $5,000 USHJA National Hunter Derby - Open $1,000 U/25 $10,000 1.35m Open Classic 2’-2’3” Child/Adult Hunter Derby $15,000 1.40m Open Classic 2’6”-2’9” Child/Adult Hunter Derby $2,500 JR/A-O/AM 1.35m Classic $ 1,000 A-O 3’6 Hunter Classic $5,000 JR/A-O/AM 1.45m Classic $1,000 A-O 3’3 Hunter Classic $1,500 JR/A-O/AM 1.25m Classic $1,500 Child Jumper High Classic $1,000 Junior 3’6 Hunter Classic $1,500 Adult Jumper High Classic $1,000 Junior 3’3 Hunter Classic $450 Child Jumper Low Classic $500 NAL Adult Hunter Classic $450 Adult Jumper Low Classic $500 NAL Child Hunter Classic 1.20m Silver Oak Jumping Tour $1,500 1.20m Open Classic $500 Pony Hunter Classic $250 .75m Non Pro Jumper Classic $250 .85m Non Pro Jumper Classic $250 .95m Non Pro Jumper Classic $250 1.05m Open Jumper Classic EQUITATION PCHA JR/AM Horsemanship 2’9” Medal Finals SCHSA Challenge Medal Finals 86 | REVISED AUGUST 12, 2021 2021 NATIONAL SUNSHINE SERIES TENTATIVE SCHEDULE - HUNTERS - WEEK I TUESDAY HUNTER RING 1 - 8 AM HUNTER RING 2 - 8 AM HUNTER RING 3 HUNTER RING 4 - 8 AM HUNTER RING 5 HUNTER RING 6 HUNTER RING 7 800. Clear Round Hunter (3’3”) 801. -

Centerboard Classes NAPY D-PN Wind HC
Centerboard Classes NAPY D-PN Wind HC For Handicap Range Code 0-1 2-3 4 5-9 14 (Int.) 14 85.3 86.9 85.4 84.2 84.1 29er 29 84.5 (85.8) 84.7 83.9 (78.9) 405 (Int.) 405 89.9 (89.2) 420 (Int. or Club) 420 97.6 103.4 100.0 95.0 90.8 470 (Int.) 470 86.3 91.4 88.4 85.0 82.1 49er (Int.) 49 68.2 69.6 505 (Int.) 505 79.8 82.1 80.9 79.6 78.0 A Scow A-SC 61.3 [63.2] 62.0 [56.0] Akroyd AKR 99.3 (97.7) 99.4 [102.8] Albacore (15') ALBA 90.3 94.5 92.5 88.7 85.8 Alpha ALPH 110.4 (105.5) 110.3 110.3 Alpha One ALPHO 89.5 90.3 90.0 [90.5] Alpha Pro ALPRO (97.3) (98.3) American 14.6 AM-146 96.1 96.5 American 16 AM-16 103.6 (110.2) 105.0 American 18 AM-18 [102.0] Apollo C/B (15'9") APOL 92.4 96.6 94.4 (90.0) (89.1) Aqua Finn AQFN 106.3 106.4 Arrow 15 ARO15 (96.7) (96.4) B14 B14 (81.0) (83.9) Bandit (Canadian) BNDT 98.2 (100.2) Bandit 15 BND15 97.9 100.7 98.8 96.7 [96.7] Bandit 17 BND17 (97.0) [101.6] (99.5) Banshee BNSH 93.7 95.9 94.5 92.5 [90.6] Barnegat 17 BG-17 100.3 100.9 Barnegat Bay Sneakbox B16F 110.6 110.5 [107.4] Barracuda BAR (102.0) (100.0) Beetle Cat (12'4", Cat Rig) BEE-C 120.6 (121.7) 119.5 118.8 Blue Jay BJ 108.6 110.1 109.5 107.2 (106.7) Bombardier 4.8 BOM4.8 94.9 [97.1] 96.1 Bonito BNTO 122.3 (128.5) (122.5) Boss w/spi BOS 74.5 75.1 Buccaneer 18' spi (SWN18) BCN 86.9 89.2 87.0 86.3 85.4 Butterfly BUT 108.3 110.1 109.4 106.9 106.7 Buzz BUZ 80.5 81.4 Byte BYTE 97.4 97.7 97.4 96.3 [95.3] Byte CII BYTE2 (91.4) [91.7] [91.6] [90.4] [89.6] C Scow C-SC 79.1 81.4 80.1 78.1 77.6 Canoe (Int.) I-CAN 79.1 [81.6] 79.4 (79.0) Canoe 4 Mtr 4-CAN 121.0 121.6 -
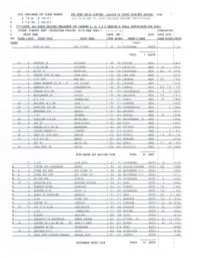
PHRF by Club (Challenge Cup)
2020 CHALLENGE CUP CLASS BREAKS GYA PHRF VALID LISTING (sorted by YACHT CLUB/NET RATING) page c A 15-72 B 75-111 (run as of MAR 18, 2020) (EXCLUDES EXPIRED CERTIFICATES) H C 114-150 D 153-213 A ****(NOTE: ALL BOATS SAILING CHALLENGE CUP CLASSES A, B, C & D REQUIRE A ORRez CERTIFICATE FOR 2020) L *CLASS: S=SPORT BOAT CF=CRUISER FURLING X="X-PHRF CERT." 1---------- 1 ICUMULATIVE I G RECOM CREW IBASE NET I CLUB IRACE DIST I CUP CLASS LIMIT YACHT TYPE YACHT NAME IRTNG RATNG I OWNER'S NAME ISPNK N/SPK ICERT# CLASS (last) 11 KING 40 ODR HOT TICKET 30 30 !HIGHTOWER AUS TN 11135 TOTAL AUS TN CF 9 EXPRESS 34 EPIPHANY 96 99 !HUNTER BBSC 3927 8 J-29 OB MH STICKMAN 114 114 !GRIFFITH BBSC 22 3910 CF 10 ELITE 37 MAVERICK 120 126 !HUTCHISON BBSC 387 41 2799 CF 11 TARTAN 3800 SD MOD TRUE GRIT 120 126 !VAN VOST BBSC 4123 7 J-80 ODR MUD BUG 132 129 !GWINNUP BBSC 596 1623 8 GOMAN EXPRESS 30 SD 1-57 IDA CLAIRE 150 147 !VACCARO BBSC 4134 CF 9 PEARSON 33-2 PANDEMONIUM 150 156 !DEMING BBSC 293 136 109 CF 9 TARTAN 34-2 SD VIXEN 141 165 !LAUDERBAUGH BBSC 16 11 3564 6 WAVELENGTH 24 AVOCET 168 168 IBALLASCH BBSC 155 1612 7 S-2 7 . 9 SHENANIGAN 171 171 !STACY BBSC 46 3892 CF 9 ERICSON 32-3 WK LADY J 162 177 !JOHNSEN BBSC 4023 CF 10 CATALINA 350 WK IRISH LADY 159 180 IEDENBOROUGH BBSC 11 3886 CF 9 BENETEAU 3 31 ADAGIO 153 183 I GWINNUP BBSC 4191 5 J-22 UNTAMED 177 183 !HUNTER BBSC 39 3790 CF 8 CATALINA 310 DK WHITS END 168 186 !WHITTEMORE , JR . -

2019 PHRF-LO Championship Standings-26
26 August 2019 Boat Name Class Club District Sail# FS NFS Score It’s a Conspiracy S2 9.1 BHYC GHPRF 40323 129 150 384.9 Midnight Express Goman Exp 30-2 SD HYC TORE 74169 145 165 348.2 Oz J 24 Oswego YC RDPRF 1731 164 182 346.5 Pandora II CS 33 BSBC GHPRF 3386 149 164 339.4 4 Tuna C&C 35-3 ABYC TORW 34435 127 144 338.2 Snowbird Niagara 26 OB BSBC GHPRF 100 185 200 330.8 Nights Watch C&C 27-5 National YC TORW 53 178 198 328.2 Magic C&C 35-2 DYC SSYRA 11335 142 167 319.4 Beyond Survival C&C 115 CF BC TORW 54266 65 91 310.3 Perry-Eh Evelyn 32-2 RHYC GHPRF 53337 105 132 309.4 Give’r J 88 CF SB National YC TORW CAN 84 85 120 302.7 Blast Beneteau 1st 10R CF MCC TORW CAN 42 87 112 300.2 Battlewagon J 35 BSBC GHPRF 210 72 93 299.4 Volga Beneteau Oceanis 34 MCC TORW CAN 1026 159 191 285.6 Carina Catalina 309 WK PCYC TORW 141 - 227 284.4 Blown Away Ranger 22 RHYC GHPRF 334 - 234 282.4 Caprice Capri 25 RHYC GHPRF 189 171 188 280.6 Jersey Girl Olson 911S PCYC TORW 42264 124 144 273.4 Sabotage Viper 830 CF SB RHYC GHPRF 106 41 63 272.2 Ariadna Beneteau 1st 36.7 EYC TORW 51975 80 98 271.0 Blaze J 30 Oswego YC RDPRF 43225 130 149 270.4 Xoomer Xpress X 35 National YC TORW 146 68 96 270.1 Serious C&C 33-2 OC GHPRF 74 132 153 267.2 Promises Promises Pearson 30 Crescent YC EYC 14148 165 186 266.2 Live Wire J 109 PCYC TORW 144 75 100 264.5 Mythos CS 36 Merlin WK PCYC TORW 6204 146 160 261.3 Nauti-Buoy Tanzer 22 MOD BSBC GHPRF 1923 223 243 260.7 Moongator S2 7.9 IB Sodus Bay YC RDPRF 100 171 189 257.7 Katbird Dufour 34 Performance RCYC TORW 54402 123 146 256.5 Peppermint Tanzer 22 NSC EYC 1568 222 242 255.4 Mr. -

2019 PHRF-LO Championship Standings-18 June 2019
18 June 2019 Boat Name Class Club District Sail# FS NFS Score Ariadna Beneteau 1st 36.7 EYC TORW 51975 80 98 195.3 Lively J 109 ABYC TORW 265 72 96 195.1 Maroca II CS 36 Merlin WK LSYC TORW 6226 - 160 179.5 High Tea J 112E MCC TORW 72 77 104 176.7 Live Wire J 109 PCYC TORW 144 75 100 173.7 Sea Ya Farr 39ML SB MCC TORW 50939 31 53 171.6 Suspect Perry 58 CF BHYC GHPRF 13667 -3 20 167.7 Mythos CS 36 Merlin WK PCYC TORW 6204 146 160 165.1 Katbird Dufour 34 Performance RCYC TORW 54402 123 146 164.5 Entourage Olson 911S Ericson LSYC TORW 50229 127 149 164.3 Byte Size Catalina 36 TM LSYC TORW 25132 141 161 159.1 Umi Taka C&C 35-3 ABYC TORW 32835 123 144 158.1 Mr. Ed IMX 38 PCYC TORW 51166 67 86 155.1 Upstart Jeanneau 3200 Sun Fast MOD CF BPYC TORE 629 87 114 153.0 Xoomer Xpress X 35 National YC TORW 146 68 96 152.2 The Cat Came Back J 120 CF ABYC TORW 51790 50 78 150.6 Jersey Girl Olson 911S PCYC TORW 42264 124 144 150.4 Doralla C&C 27-3 RCYC TORW 54048 190 210 148.5 Puffin C&C 30 SD MCC TORW 11778 173 191 140.9 Blew By U Islander 36 National YC TORW 13608 142 169 138.8 Screaming Eagle Beneteau 1st 42 TM EYC TORW 84442 85 107 138.7 Midnight Express Goman Exp 30-2 SD HYC TORE 74169 145 165 137.5 Give’r J 88 CF SB National YC TORW CAN 84 85 120 136.1 Hot Water J 133 SB MCC TORW 54375 22 51 131.8 Setanta Hanse 400 PCYC TORW 227 88 104 130.7 Worthy Pearl C&C 37 EYC TORW 51370 110 134 130.4 Still Knot Working C&C 27-5 EYC TORW 75 178 198 129.5 4 Tuna C&C 35-3 ABYC TORW 34435 127 144 129.0 Arriba Beneteau 1st 36.7 LSYC TORW 60189 78 96 124.2 Nights -
You Can Do It! 3 Top Charter Destinations: • Antigua • Dominica • Eleuthera
You Can Do It! 3 Top Charter Destinations: • Antigua • Dominica • Eleuthera BOAT REVIEWS: • New! Cruisers Yachts 390 • Jeanneau Sun Odyssey 349 Pacific Coast San Juan Islands October 2014 $6.95 CDN + CANADIANYACHTING.CA www.mainship.com a Feel the Quality… Experience the Value. A statement from Mr. David E. Marlow, Chairman and Owner of Marlow-Hunter, LLC continuous striving to be better expressed in in-mast furling and electric winches and you words that attempt to describe the passion have a boat that is much easier to sail and will and dedication of all our employees and out sail its competitors all things being equal owner subscribe to make the boat of your in virtually all conditions. Our goal is to get dreams come true… be it that daysailor or you on the water faster and safer, with more ocean voyager. comfort than ever before while aboard. SAFETY – OUR HIGHEST CONCERN EASE OF SAILING THROUGH INNOVATION All Marlow boats are constructed to NMMA Over the years Hunter and now Marlow- Hunter have introduced to the production (National Marine Manufacturing Association) certification using ABYC (American Boat and sailing industry unique innovations to make Yacht Council) standards and we are a fully sailing easier and has caused many other accredited CE Certified (Community of Europe) brands to follow, albeit at times lacking the functionality or thought of original design. manufacturer which means that we can and do build boats to be shipped anywhere in Features such as stern rail seats for clearing the cockpit and giving your family and guests the world meeting that country’s standards. -

11 Meter Od Odr *(U)* 75 1D 35 36 1D 48
11 METER OD ODR *(U)* 75 1D 35 36 1D 48 -42 30 SQUARE METER *(U)* 138 5.5 METER ODR *(U)* 156 6 METER ODR *(U)* Modern 108 6 METER ODR *(U)* Pre WW2 150 8 METER Modern 72 8 METER Pre WW2 111 ABBOTT 33 126 ABBOTT 36 102 ABLE 20 288 ABLE 42 141 ADHARA 30 90 AERODYNE 38 42 AERODYNE 38 CARBON 39 AERODYNE 43 12 AKILARIA class 40 RC1 -6/3 AKILARIA Class 40 RC2 -9/0 AKILARIA Class 40 RC3 -12/-3 ALAJUELA 33 198 ALAJUELA 38 216 ALBERG 29 225 ALBERG 30 228 ALBERG 35 201 ALBERG 37 YAWL 162 ALBIN 7.9 234 ALBIN BALLAD 30 186 ALBIN CUMULUS 189 ALBIN NIMBUS 42 99 ALBIN NOVA 33 159 ALBIN STRATUS 150 ALBIN VEGA 27 246 Alden 42 CARAVELLE 159 ALDEN 43 SD SM 120 ALDEN 44 111 ALDEN 44-2 105 ALDEN 45 87 ALDEN 46 84 ALDEN 54 57 ALDEN CHALLENGER 156 ALDEN DOLPHIN 126 ALDEN MALABAR JR 264 ALDEN PRISCILLA 228 ALDEN SEAGOER 141 ALDEN TRIANGLE 228 ALERION XPRS 20 *(U)* 249 ALERION XPRS 28 168 ALERION XPRS 28 WJ 180 ALERION XPRS 28-2 (150+) 165 ALERION XPRS 28-2 SD 171 ALERION XPRS 28-2 WJ 174 ALERION XPRS 33 120 ALERION XPRS 33 SD 132 ALERION XPRS 33 Sport 108 ALERION XPRS 38Y ODR 129 ALERION XPRS 38-2 111 ALERION XPRS 38-2 SD 117 ALERION 21 231 ALERION 41 99/111 ALLIED MISTRESS 39 186 ALLIED PRINCESS 36 210 ALLIED SEABREEZE 35 189 ALLIED SEAWIND 30 246 ALLIED SEAWIND 32 240 ALLIED XL2 42 138 ALLMAND 31 189 ALLMAND 35 156 ALOHA 10.4 162 ALOHA 30 144 ALOHA 32 171 ALOHA 34 162 ALOHA 8.5 198 AMEL SUPER MARAMU 120 AMEL SUPER MARAMU 2000 138 AMERICAN 17 *(U)* 216 AMERICAN 21 306 AMERICAN 26 288 AMF 2100 231 ANDREWS 26 144 ANDREWS 36 87 ANTRIM 27 87 APHRODITE 101 135 APHRODITE -

North American Portsmouth Yardstick Table of Pre-Calculated Classes
North American Portsmouth Yardstick Table of Pre-Calculated Classes A service to sailors from PRECALCULATED D-PN HANDICAPS CENTERBOARD CLASSES Boat Class Code DPN DPN1 DPN2 DPN3 DPN4 4.45 Centerboard 4.45 (97.20) (97.30) 360 Centerboard 360 (102.00) 14 (Int.) Centerboard 14 85.30 86.90 85.40 84.20 84.10 29er Centerboard 29 84.50 (85.80) 84.70 83.90 (78.90) 405 (Int.) Centerboard 405 89.90 (89.20) 420 (Int. or Club) Centerboard 420 97.60 103.40 100.00 95.00 90.80 470 (Int.) Centerboard 470 86.30 91.40 88.40 85.00 82.10 49er (Int.) Centerboard 49 68.20 69.60 505 (Int.) Centerboard 505 79.80 82.10 80.90 79.60 78.00 747 Cat Rig (SA=75) Centerboard 747 (97.60) (102.50) (98.50) 747 Sloop (SA=116) Centerboard 747SL 96.90 (97.70) 97.10 A Scow Centerboard A-SC 61.30 [63.2] 62.00 [56.0] Akroyd Centerboard AKR 99.30 (97.70) 99.40 [102.8] Albacore (15') Centerboard ALBA 90.30 94.50 92.50 88.70 85.80 Alpha Centerboard ALPH 110.40 (105.50) 110.30 110.30 Alpha One Centerboard ALPHO 89.50 90.30 90.00 [90.5] Alpha Pro Centerboard ALPRO (97.30) (98.30) American 14.6 Centerboard AM-146 96.10 96.50 American 16 Centerboard AM-16 103.60 (110.20) 105.00 American 17 Centerboard AM-17 [105.5] American 18 Centerboard AM-18 [102.0] Apache Centerboard APC (113.80) (116.10) Apollo C/B (15'9") Centerboard APOL 92.40 96.60 94.40 (90.00) (89.10) Aqua Finn Centerboard AQFN 106.30 106.40 Arrow 15 Centerboard ARO15 (96.70) (96.40) B14 Centerboard B14 (81.00) (83.90) Balboa 13 Centerboard BLB13 [91.4] Bandit (Canadian) Centerboard BNDT 98.20 (100.20) Bandit 15 Centerboard -

Massey Yacht Sales Hunter Sold Boat Report for May 2019
This is a monthly sold boat report. If you would like an expanded report please contact, Ed Massey at [email protected] or 941-725-2350 Massey Yacht Sales Hunter Sold Boat Report for May 2019 Date % of Year Listed US$ Listed Sold US$ Sold Date Location Mos to Sell Listed$ 46' Hunter 466 2004 174,500 Mar-18 161,750 May-19 NC, USA 15 93% 46' Hunter 466 2002 155,000 Mar-19 138,000 May-19 MD, USA 3 89% 46' Hunter 466 LE 2006 159,000 Mar-19 150,000 May-19 FL, USA 3 94% 46' Hunter Passage 456 2005 179,500 Mar-19 169,500 May-19 CA, USA 3 94% 45' Hunter 45 Deck Salon 2010 189,900 Jul-16 185,000 May-19 MI, USA 35 97% 45' Hunter 45 LEGEND 1987 59,500 Oct-18 55,000 May-19 MA, USA 8 92% 45' Hunter 45cc 2006 189,900 Dec-18 156,000 May-19 WA, USA 6 82% 41' Hunter 40.5 1997 79,500 Sep-18 65,000 May-19 CA, USA 9 82% 41' Hunter 410 2003 86,900 Nov-18 72,500 May-19 FL, USA 7 83% 41' Hunter 410 2002 99,900 Feb-19 90,000 May-19 MD, USA 4 90% 41' Hunter 410 1998 104,900 Dec-18 98,000 May-19 WA, USA 6 93% 40' Hunter 40 1985 42,500 Oct-18 42,000 May-19 MD, USA 8 99% 40' Hunter 40.5 1996 79,900 Oct-18 62,300 May-19 CA, USA 8 78% 40' Hunter 40.5 Wing Keel 1995 79,900 Jan-19 76,000 May-19 FL, USA 5 95% 38' Hunter 386 2003 85,000 Dec-17 75,000 May-19 NY, USA 18 88% 37' Hunter 37 1987 39,800 Aug-18 37,500 May-19 OH, USA 10 94% 37' Hunter 37' Cherubini Cutter 1979 12,000 Apr-17 12,000 May-19 KY, USA 26 100% 37' Hunter 376 1997 65,000 Mar-19 65,000 May-19 CT, USA 3 100% 37' Hunter 376 1997 62,900 Apr-19 58,000 May-19 CA, USA 2 92% 37' Hunter 376 1996 44,900 -
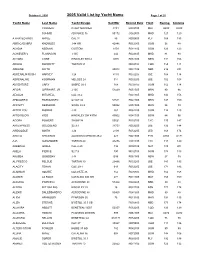
Valid List by Yacht Name Page 1 of 25
October 6, 2005 2005 Valid List by Yacht Name Page 1 of 25 Yacht Name Last Name Yacht Design Sail Nbr Record Date Fleet Racing Cruising CORREIA O DAY MARINER 3181 R032105 MAT U294 U300 SCHMID ADVANCE 36 50172 C062805 MHD 123 129 A FRAYED KNOT APPLE CAL 31 85 R050805 PLY 168 183 ABRACADABRA KNOWLES J 44 WK 42846 R052905 GOM 36 48 ACADIA KEENAN CUSTOM 1001 R041105 GOM 123 123 ACHIEVER V FLANAGAN J 105 442 R022605 MHD 81 90 ACTAEA CONE HINCKLEY B40-3 3815 R061305 NEW 144 156 ADAJIO DOHERTY TARTAN 31 N082105 COD 159 171 ADELINE SCITO 20914 N081105 NBD 216 231 ADRENALIN RUSH HARVEY J 24 4139 R052205 JBE 168 174 ADRENALINE KOOPMAN MELGES 24 514 R052205 JBE 102 108 ADVENTURE CARY SABRE 30-3 168 R032705 GOM 162 174 AEGIR GIERHART, JR. J 105 51439 R051505 MRN 90 96 AEOLUS MITCHELL CAL 33-2 R021305 MHD 144 156 AEQUOREAL RASMUSSEN O DAY 34 51521 R041005 MRN 147 159 AFFINITY DESMOND SWAN 48-2 50922 R051505 MRN 36 39 AFTER YOU MORRIS J 80 261 R062205 GOM 114 123 AFTERGLOW WEG HINCKLEY SW 43TM 43602 R041105 GOM 84 96 AGORA POWERS SHOW 34 50521 R032705 CYC 135 147 AIR EXPRESS GOLDBERG S2 9.1 31753 R052205 JBE 132 144 AIRDOODLE SMITH J 24 2109 R052205 JEB 168 174 AIRTHA SPIECKER ALERION EXPRESS 28-2 227 R021305 PTS U165 U171 AJA ALEXANDER TARTAN 40 41276 C081105 CYC 117 120 AKEEPAH GRAUL CAL 2-29 146 R050105 NHT 189 201 AKELA PIERCE S2 7.9 390 N032705 GOM 174 183 AKUBBA GOODDAY J 44 B96 R061905 NEW 27 39 AL FRESCO PELSUE TARTAN 30 20486 R052205 JBE 183 195 ALACITY TEHAN C&C 29-1 643 R052205 JBE 174 186 ALANNAH SQUIRE COLGATE 26 152 R070605 MHD 162 168 -
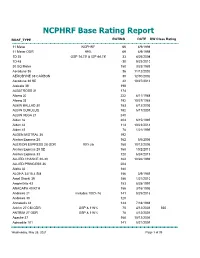
NCPHRF Base Rating Report
NCPHRF Base Rating Report BOAT_TYPE RATING DATE DW Class Rating 11 Meter NCPHRF 66 4/9/1998 11 Meter ODR 99% 69 4/9/1998 1D 35 OSP 14.75' & ISP 44.78' 33 4/26/2004 1D 48 -30 9/23/2010 30 SQ Meter 150 3/23/1989 Aerodyne 38 36 11/12/2002 AERODYNE 38 CARBON 30 12/30/2002 Aerodyne 38 SD 42 10/27/2016 Alajuela 38 198 ALBATROSS 31 174 Alberg 30 222 8/11/1988 Alberg 35 192 10/27/1988 ALBIN BALLAD 30 183 8/12/2003 ALBIN CUMULUS 192 5/17/2001 ALBIN VEGA 27 240 Alden 32 204 6/15/1995 Alden 44 114 10/23/2014 Alden 45 78 1/21/1999 ALDEN MISTRAL 36 192 Alerion Express 28 162 5/6/2006 ALERION EXPRESS 28 ODR 90% jib 168 10/12/2006 Alerion Express 28 SD 168 10/2/2013 Alerion Express 33 120 6/24/2019 ALLIED CHANCE 30-30 162 10/26/1994 ALLIED PRINCESS 36 204 Aloha 32 180 ALOHA 34/10.4 SM 156 3/9/1989 Amel Sharki 39 186 1/21/2010 Amphritrite 43 153 8/28/1991 ANACAPA 40 KTH 156 3/16/1995 Andrews 21 includes 100% hs 141 8/25/2016 Andrews 30 120 Annapolis 44 144 7/18/1988 Antrim 27 CM ODR OSP & 116% 75 4/12/2001 555 ANTRIM 27 ODR OSP & 116% 78 4/12/2001 Apache 37 168 10/12/2006 Aphrodite 101 141 5/21/2009 Wednesday, May 26, 2021 Page 1 of 39 BOAT_TYPE RATING DATE DW Class Rating Aquarius 21 288 1/21/2019 Archambault 27 w/ 12.2' spl & 105% hs 78 4/23/2015 Aries 31 258 Aries 32 234 6/29/1989 Atkin 38 183 4/8/1999 Azzura 310 57 12/7/1995 B 30 ludes square-top main & small 78 3/29/2021 B-25 141 7/1/1999 B-25 ODR 135 7/1/1999 Baba 30 240 Baba 35 SM 192 3/12/1998 Baba 40 144 2/16/1989 Baba 40 TM 138 6/18/1992 Bahama 25 252 Balboa 26 FK 222 Balboa 26 SK 228 BALBOA -

Race Analysis Report Detail for Non-Flying Sails Sorted by Club ID
Performance Handicap Racing Fleet Race Analysis Report Detail for Non-Flying Sails Sorted By Club ID 2015 - 2019 Report Parameters Year(s): 2015 To: 2019 Division: Non-Flying SailsClasses: All Classes Club: All Clubs Report is Sorted By: ClubID EventYear EventDesc BoatName Report Level Is: Detail Boats with St/Dev >50 Or St/Dev < -50 are Flagged Boats with ASP Diff >50 Or ASP Diff < -999 are Flagged Boats with Less Than3 Races are Flagged Boats with No Valid Certificate are Included Data Notes In Race Analysis Detail Clubs with combined racing are listed with a unique "Club" code Criteria used to determine if data would be included and used in BCTS (Boulevard Club Toronto Sailing Canoe Club) Summary Analysis BLUFFS (Cathedral Bluffs, Highland and Bluffers Park) BRNS (Brittania Nepean Sailing Clubs) STD DEVmust be < +/- 50 BSRH (Burlington Sailing Royal Hamilton) CALC DIFFmust be < + 50 CYCHH (Cresent YC Henderson Harbour) EAST (Eastern Area combined racing) Results that have been excluded are Flagged with * NLYY (Niagara on the Lake Youngstown) OAKV (Oakville YC and Oakville Yacht Squadrroon December 16, 2019 Page 1 of 52 Race Analysis Report (Detail) Calc# Std Calc Year Club Class Event Description Yacht NameOwner ASP ASP Races Dev Diff 2015 ABYC C&C 3/4 TON DIV 4 DOUBLE TIME ROBBINS, 174 166 20 16.4 -8 2015 ABYC ABBOTT 33 DIV 4 KOKANEE STEENBE 147 142 10 13.4 -5 2015 ABYC BENETEAU 1ST 36.7 SD DIV 4 LIONS DEN II HANNAH, 110 112 16 18 +2 2015 ABYC C&C 34 ** DIV 4 MINERVE CLOUTIE 167 173 18 24.8 +6 2015 ABYC C&C 35-3 DIV 4 QUICKSILVER