Reducing the Cost of Implementing Filters in Lora Devices
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Spatial Positioning with Wireless Chirp Spread Spectrum Ranging
JACOBS UNIVERSITY BREMEN Spatial Positioning with Wireless Chirp Spread Spectrum Ranging by Hamed Bastani A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Smart Systems School of Engineering and Science Defense date: 13 November 2009 ii Spatial Positioning with Wireless Chirp Spread Spectrum Ranging by Hamed Bastani thesis submitted in partial fulfillment for the degree of Doctor of Philosophy in Faculty of Smart Systems School of Engineering and Science Jacobs University Bremen APPROVED: Prof. Dr. Andreas Birk Supervisor, Dissertation Committee Head (Jacobs University Bremen, Germany) Prof. Dr. J¨urgenSch¨onw¨alder Dissertation Committee Member (Jacobs University Bremen, Germany) Dr. Holger Kenn Dissertation Committee Member (European Microsoft Innovation Center, Aachen, Germany) Electronic Version (10 Dec. 2009), Information Resource Center, Jacobs University. Declaration of Authorship This dissertation is submitted in partial fulfillment of requirements for a PhD degree in Smart Systems from the School of Engineering and Science at Jacobs University Bremen. The author declares that the work presented here is his own, to the best of his knowledge and belief, is written independently and has not been submitted substantially or as a whole at another University or institution for con- ferral of any other degree. The effort was done mainly while in candidature for a professional degree at this university. Where any part of this material has previ- ously been submitted in the form of a journal or conference contribution, it has been stated. Respecting the copyright boundaries, the author may use partially some parts of this thesis in the future for potential publications, investigations or improvements. -

On the Lora Modulation for Iot: Waveform Properties and Spectral Analysis Marco Chiani, Fellow, IEEE, and Ahmed Elzanaty, Member, IEEE
ACCEPTED FOR PUBLICATION IN IEEE INTERNET OF THINGS JOURNAL 1 On the LoRa Modulation for IoT: Waveform Properties and Spectral Analysis Marco Chiani, Fellow, IEEE, and Ahmed Elzanaty, Member, IEEE Abstract—An important modulation technique for Internet of [17]–[19]. On the other hand, the spectral characteristics of Things (IoT) is the one proposed by the LoRa allianceTM. In this LoRa have not been addressed in the literature. paper we analyze the M-ary LoRa modulation in the time and In this paper we provide a complete characterization of the frequency domains. First, we provide the signal description in the time domain, and show that LoRa is a memoryless continuous LoRa modulated signal. In particular, we start by developing phase modulation. The cross-correlation between the transmitted a mathematical model for the modulated signal in the time waveforms is determined, proving that LoRa can be considered domain. The waveforms of this M-ary modulation technique approximately an orthogonal modulation only for large M. Then, are not orthogonal, and the loss in performance with respect to we investigate the spectral characteristics of the signal modulated an orthogonal modulation is quantified by studying their cross- by random data, obtaining a closed-form expression of the spectrum in terms of Fresnel functions. Quite surprisingly, we correlation. The characterization in the frequency domain found that LoRa has both continuous and discrete spectra, with is given in terms of the power spectrum, where both the the discrete spectrum containing exactly a fraction 1/M of the continuous and discrete parts are derived. The found analytical total signal power. -

Towards Robust High Speed Underwater Acoustic Communications Using Chirp Multiplexing
Towards Robust High Speed Underwater Acoustic Communications Using Chirp Multiplexing Jiacheng Shi, Emrecan Demirors, and Tommaso Melodia Department of Electrical and Computer Engineering, Northeastern University, Boston, MA 02115 E-mail:{shijc, edemirors, melodia}@ece.neu.edu Abstract—Wide band chirp spread spectrum (CSS) has been studied in underwater acoustic (UWA) communications to guar- antee low bit error rates with low transmission rates. On the other hand, high speed transmission schemes for UWA, especially Orthogonal-Frequency-Division-Multiplexing (OFDM) technol- ogy, can reach Mbit/s data rates but at the expense of reliability. In this paper, we propose a new transmission scheme based on multiplexing information bits to (quasi-)orthogonal chirp signals, called Quasi-Orthogonal Chirp Multiplexing (QOCM). It can be easily implemented on reprogrammable hardware as an extension to OFDM architectures. We evaluated the performance of the proposed scheme with simulation and tank experiments. Results show that QOCM scheme is able to achieve one order of magnitude better performance than an OFDM scheme under severe Doppler effect posed by simulation in long distance water transmission. Moreover, we observe in water tank experiment that the QOCM scheme is resilient against to the Doppler effects induced by relative speeds up to 5 knots, which corresponds to 214.16 Hz 125 kHz a Doppler shift of at a center frequency of . Fig. 1: An example of M = 4 chirp subcarriers with N = Index Terms—Underwater acoustic communications, chirp multiplexing, robust. 8 samples per subcarrier and processing gain K = 2. The figure shows the frequency changes of each subcarrier over time index n. The information bits for this transmission are 0,1,1,0. -
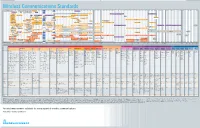
Wireless Communications Standards
Wireless Communications Standards 70 Tetrapol 520 764 Project 25 870 890 915 BeiDou B3 2400 ISM Band 2.4 GHz 2485 ISM Band 5 GHz 5725 ISM Band 5 GHz 5825 mmWave Band SUL Band 81 1268.52 BeiDou B1 1880 1930 1575.42 DECT 250 LR-WPAN 750 779 787 806 UL 825 TETRA 851 DL 870 902WLAN 928 BeiDou B2 LR-WPAN IEEE 802.11ah 1191.79 1695 1710 1995 2020 451 UL 456 461 DL 466 IRNSS L5 (E-)UTRA/FDD Band 70 2360 2483.5 3244 LR-WPAN 4742 FDD Band 72 1176.45 UL DL LR-WPAN, ZigBee 3.0, Thread, 6LoWPAN 380.2 UL 389.8 390.2 DL 399.8 747 DL 763 777 UL 793 863 879 896 960 1427 1518 1850 UL 1910 PCS 1900 1930 DL 1990 T-GSM 380 GSM 750 LR-WPAN LR-WPAN LR-WPAN IRNSS S 410.2 UL 419.8 420.2 DL 429.8 863 870 902 928 1427 1432 1710 UL 1785 1805 DL 1880 2492.028 FDD Band 76 DCS 1800 T-GSM 410 LPWAN LPWAN 3600 3800 1427 1432 880 UL 915 925 DL 960 (E-)UTRA/TDD Band 43 450.4 UL 457.6 460.4 DL 467.6 TDD Band 51 GLONASS L1 1850 1910 1930 1990 GSM 450 E-GSM 900 1602 (E-)UTRA/TDD Band 35 (E-)UTRA/TDD Band 36 GLONASS L3 824 UL 849 GSM 850 869 DL 894 1900 1920 478.8 UL 486 488.8 DL 496 1202.025 1525 DL 1559 1626.5 UL 1660.5 2496 2690 GSM 480 (E-)UTRA/TDD Band 33 (E-)UTRA/TDD Band 41 GLONASS L2 (E-)UTRA/FDD Band 24 2305 UL 2315 2350 DL2360 698 UL 716 728 DL 746 806 UL 821 T-GSM 810 851 DL 866 890 UL 915 935 DL 960 1246 1910 1930 2010 2025 (E-)UTRA/FDD Band 30 GSM 710 P-GSM 900 (E-)UTRA/TDD Band 37 (E-)UTRA/TDD Band 34 452.5 UL 457.5 462.5 DL 467.5 832 862 873 UL 915 918 DL 960 1432 1517 1880 1920 2300 2400 2570 2620 3400 3600 (E-)UTRA/FDD Band 31 SUL Band 82 ER-GSM 900 TDD Band -

AN1200.22 Lora™ Modulation Basics
AN1200.22 LoRa™ Modulation Basics APPLICATION NOTE AN1200.22 LoRa™ Modulation Basics Revision 2, May 2015 www.semtech.com P a g e | 1 ©2015 Semtech Corporation AN1200.22 LoRa™ Modulation Basics APPLICATION NOTE Table of Contents 1 Introduction .......................................................................................................................................... 4 2 Acronyms .............................................................................................................................................. 5 3 Spread Spectrum Communications ...................................................................................................... 6 3.1 Shannon – Hartley Theorem ......................................................................................................... 6 3.2 Spread-Spectrum Principles .......................................................................................................... 7 3.3 Chirp Spread Spectrum ................................................................................................................. 9 4 LoRa Spread Spectrum .......................................................................................................................... 9 4.1 Key Properties of LoRa Modulation ............................................................................................ 11 4.1.1 Bandwidth Scalable ............................................................................................................. 11 4.1.2 Constant Envelope / Low-Power ........................................................................................ -

Analysis, Simulation, and Implementation of Block Transform OFDM Xiaoliang Xue University of Wollongong
University of Wollongong Research Online University of Wollongong Thesis Collection University of Wollongong Thesis Collections 2011 Analysis, simulation, and implementation of block transform OFDM Xiaoliang Xue University of Wollongong Recommended Citation Xue, Xiaoliang, Analysis, simulation, and implementation of block transform OFDM, Master of Engineering - Research thesis, School of Electrical, Computer and Telecommunications Engineering, University of Wollongong, 2011. http://ro.uow.edu.au/theses/3437 Research Online is the open access institutional repository for the University of Wollongong. For further information contact Manager Repository Services: [email protected]. Analysis, Simulation, and Implementation of Block Transform OFDM A thesis submitted in partial fulfilment of the requirements for the award of the degree Master of Engineering by Research from UNIVERSITY OF WOLLONGONG by Xiaoliang Xue School of Electrical, Computer and Telecommunications Engineering October 2011 Statement of Originality I, Xiaoliang Xue, declare that this thesis, submitted in partial fulfillment of the requirements for the award of Master of Engineering - Research, in the School of Electrical, Computer and Telecommunications Engineering, University of Wollongong, is wholly my own work unless otherwise referenced or acknowledged. The document has not been submitted for qualifications at any other academic institution. Xiaoliang Xue 28 March, 2011 List of Abbreviations 1G First-generation 2G Second-generation 3G Third-generation 4G Fourth-generation -

Low Complexity Equalization of Orthogonal Chirp Division Multiplexing in Doubly-Selective Channels
sensors Article Low Complexity Equalization of Orthogonal Chirp Division Multiplexing in Doubly-Selective Channels Xin Wang, Zhe Jiang and Xiao-Hong Shen * School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China; [email protected] (X.W.); [email protected] (Z.J.) * Correspondence: [email protected] Received: 1 May 2020; Accepted: 29 May 2020; Published: 1 June 2020 Abstract: Orthogonal Chirp Division Multiplexing (OCDM) is a modulation scheme which outperforms the conventional Orthogonal Frequency Division Multiplexing (OFDM) under frequency selective channels by using chirp subcarriers. However, low complexity equalization algorithms for OCDM based systems under doubly selective channels have not been investigated yet. Moreover, in OCDM, the usage of different phase matrices in modulation will lead to extra storage overhead. In this paper, we investigate an OCDM based modulation scheme termed uniform phase-Orthogonal Chirp Division Multiplexing (UP-OCDM) for high-speed communication over doubly selective channels. With uniform phase matrices equipped, UP-OCDM can reduce the storage requirement of modulation. We also prove that like OCDM, the transform matrix of UP-OCDM is circulant. Based on the circulant transform matrix, we show that the channel matrices in UP-OCDM system over doubly selective channels have special structures that (1) the equivalent frequency-domain channel matrix can be approximated as a band matrix, and (2) the transform domain channel matrix in the framework of the basis expansion model (BEM) is a sum of the product of diagonal and circulant matrices. Based on these special channel structures, two low-complexity equalization algorithms are proposed for UP-OCDM in this paper. -

A Chirp Spread Spectrum Modulation Scheme for Robust Power Line Communication Stephen Robson and Manu Haddad, Member, IEEE
1 A Chirp Spread Spectrum Modulation Scheme for Robust Power Line Communication Stephen Robson and Manu Haddad, Member, IEEE Abstract—This paper proposes the use of a LoRa like chirp This paper proposes a PLC modulation scheme based on spread spectrum physical layer as the basis for a new Power Line the Chirp Spread Spectrum (CSS) scheme of the recently stan- Communication modulation scheme suited for low-bandwidth dardised LoRa physical layer [4]. The modification is designed communication. It is shown that robust communication can be established even in channels exhibiting both extreme multipath to combat the two major problems of extreme multipath and interference and low SNR (-40dB), with synchronisation require- low SNR. The former is resolved by subdividing the LoRa ments significantly reduced compared to conventional LoRa. symbol into a reduced set, thereby containing the multipath ATP-EMTP simulations using frequency dependent line and energy into a single symbol. The latter is resolved through the transformer models, and simulations using artificial Rayleigh use of statistical averaging of the modified signal over consec- channels demonstrate the effectiveness of the new scheme in providing load data from LV feeders back to the MV primary utive symbols. This trading off of data rate for performance substation. We further present experimental results based on a makes possible a communication scheme in which many LV Field Programmable Gate Array hardware implementation of feeder monitoring devices can communicate back to a primary the proposed scheme. substation at timescales of several seconds or minutes. Index Terms—PLC, LoRa, LV Monitoring. II. BACKGROUND A. Requirements for Robust Communication on the LV-MV I. -

Wireless Temperature and Humidity Presentation Slides
Wireless Monitoring for GxP & Controlled Environments Learn about Modern RF Communication using VaiNet as an example Paul Daniel Sr. GxP Regulatory Expert [email protected] © Vaisala Vaisala in Brief . We serve customers in weather and controlled environment markets . 80 years of experience in providing a comprehensive range of innovative observation and measurement products and services © Vaisala 2 Vaisala in Brief . We serve customers in weather and controlled environment markets . 80 years of experience in providing a comprehensive range of innovative observation and measurement products and services © Vaisala 3 Vaisala in Brief . We serve customers in weather and controlled environment markets . 80 years of experience in providing a comprehensive range of innovative observation and measurement products and services © Vaisala 4 Wireless Monitoring for GxP & Controlled Environments Learn about Modern RF Communication using VaiNet as an example Paul Daniel Sr. GxP Regulatory Expert [email protected] © Vaisala © Vaisala 6 Goals . Learn: Communication Technology Basics . Radio waves, Modulation, and Link Budgets . Explore: Internet of Things . LoRa® Technology . VaiNet Architecture . Connectivity for Monitoring . Ethernet, VaiNet, Wi-Fi, Bluetooth, ZigBee © Vaisala 7 Internet Evolution: Servers and Clients © Vaisala 8 Wired: Ethernet . Range: . Less than 100m . Power: . Available as PoE (Power over Ethernet) . Security: . Physical network access required . Reliability: . Wired full duplex connections are reliable . Flexibility: . Hard to move network drops . Investment: . One drop per sensor © Vaisala 9 Internet Evolution: Wireless © Vaisala 10 Wireless: Wi-Fi . Range: . Maximum 20m . Power: . High power required . Security: . Difficult to secure . Reliability: . Signal strength can change . Flexibility: . High flexibility . Investment: . Wi-Fi Access Points only © Vaisala 11 Internet Evolution: Things © Vaisala 12 Wireless: VaiNet . -

Analysis of Chirp Spread Spectrum System for Multiple Access
International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 1 Issue 3, May - 2012 Analysis of Chirp Spread Spectrum System for Multiple Access Rajni Billa Pooja Sharma Javed Ashraf M. Tech Scholar M. Tech Scholar Asst. Professor Department of Electronics Department of Electronics Department of Electronics and Communication and Communication and Communication AFSET, Faridabad, India AFSET, Faridabad, India AFSET, Faridabad, India E-mail: E-mail: E-mail: [email protected] [email protected] [email protected] Abstract 1. Introduction This paper evaluates the performance of an efficient Through the years, the Federal Communication chirp spread spectrum multiple access technique. The Commission (FCC) managed the spectrum allocations technique is motivated by the inherent interference on a request-by-request basis; the FCC has realized that rejection capability of such spread-spectrum type it had no more spectra to allocate [5], which gave rise system, especially in circumstances where immunity to spread spectrum techniques. With the rapid against Doppler shift and fading due to multipath development in wireless communication, spread propagation are important. Linear chirp of different spectrum techniques and spread spectrum systems have chirp rates and phases spreads the modulated signal, received quite some attention. As a future that creates a pseudo-orthogonal set of spreading communication systems a spread spectrum system has codes. An efficient system for spread spectrum multiple the advantage of inherent detection protection due to access can be made by combining linear chirp their noise-like spectra, interference rejection, modulation with polar signaling, which reduces the multipath suppression, code division multiple access, multiple access interference. -

Characterizing the Impact of Doppler Effects on Body-Centric Lora Links with SDR
sensors Article Characterizing the Impact of Doppler Effects on Body-Centric LoRa Links with SDR Thomas Ameloot 1,* , Marc Moeneclaey 2 , Patrick Van Torre 1 and Hendrik Rogier 1 1 IDLab, Department of Information Technology (INTEC), Ghent University-imec, Technologiepark-Zwijnaarde 126, B-9052 Ghent, Belgium; [email protected] (P.V.T.); [email protected] (H.R.) 2 Department of Telecommunications and Information Processing (TELIN), Ghent University, Sint-Pietersnieuwstraat 41, B-9000 Ghent, Belgium; [email protected] * Correspondence: [email protected]; Tel.: +32-9-331-4881 Abstract: Long-range, low-power wireless technologies such as LoRa have been shown to exhibit excellent performance when applied in body-centric wireless applications. However, the robustness of LoRa technology to Doppler spread has recently been called into question by a number of researchers. This paper evaluates the impact of static and dynamic Doppler shifts on a simulated LoRa symbol detector and two types of simulated LoRa receivers. The results are interpreted specifically for body-centric applications and confirm that, in most application environments, pure Doppler effects are unlikely to severely disrupt wireless communication, confirming previous research, which stated that the link deteriorations observed in a number of practical LoRa measurement campaigns would mainly be caused by multipath fading effects. Yet, dynamic Doppler shifts, which occur as a result of the relative acceleration between communicating nodes, are also shown to contribute to link degradation. This is especially so for higher LoRa spreading factors and larger packet sizes. Keywords: Internet of Things; LoRa; body-centric communication; software defined radio; doppler Citation: Ameloot, T.; Moeneclaey, M.; Van Torre, P.; Rogier, H. -

Towards an SDR Implementation of Lora: Reverse-Engineering
Towards an SDR implementation of LoRa: Reverse-engineering, demodulation strategies and assessment over Rayleigh channel Alexandre Marquet, Nicolas Montavont, Georgios Papadopoulos To cite this version: Alexandre Marquet, Nicolas Montavont, Georgios Papadopoulos. Towards an SDR implementation of LoRa: Reverse-engineering, demodulation strategies and assessment over Rayleigh channel. Computer Communications, Elsevier, In press, 10.1016/j.comcom.2020.02.034. hal-02485052 HAL Id: hal-02485052 https://hal.archives-ouvertes.fr/hal-02485052 Submitted on 19 Feb 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Towards an SDR Implementation of LoRa: Reverse-engineering, Demodulation Strategies and Assessment over Rayleigh Channel Alexandre Marquet, Nicolas Montavont, Georgios Z. Papadopoulos IMT Atlantique, IRISA, UBL, F-35576 Cesson S´evign´e,France. Abstract LoRa is a popular low-rate, Low-Power Wide Area Network (LPWAN) technology providing long range wireless access over unlicensed sub-GHz frequency bands to the Internet of Things (IoT). It has been used in many applications ranging from smart building to smart agriculture. LoRa is a patented modulation. However preliminary reverse-engineering efforts documented parts of it. In this article, we detail the different stages of LoRa transceivers: channel (de)coding, (de)whitening, (de)interleaving and (de)modulation with reverse-engineering in mind.