Zbwleibniz-Informationszentrum
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

香港物業管理公司協會有限公司the Hong Kong Association of Property Management Companies Limited
香港物業管理公司協會有限公司 The Hong Kong Association of Property Management Companies Limited 會員轄下物業資料 Date : 05-29-2019 Members Portfolios Property Registers 會員編號 F-0060/99 公司名稱: 冠威管理有限公司 Membership No.: Company Name: Goodwill Management Limited 總樓宇面積 單位面積 (平方呎) 類別 物業名稱及地點 物業地址 類別/座數 單位數目 Unit Size GFA 樓齡 管理年數 Type Properties Properties Address Type/No. of Blocks No. of Units Min/Max Sq. Ft. Age Yrs.Managed CAIA Tower 183 Electric Road North Point HK 515645.00 21.0 21.0 CDawning Views Plaza 23 Yat Ming Rd Fanling NT 96365.00 19. 11 19. 11 CFanling Centre Shopping Arcade 33 San Wan Road Fanling NT 151513.00 28. 5 28. 5 CFWD Financial Centre 308-320 Des Voeux Rd C HK 225851.00 24. 7 24. 7 CGolden Centre 188 Des Voeux Rd Central HK 156562.00 28. 2 28. 2 CGrand Waterfront Plaza 38 San Ma Tau Street Ma Tau Kok KLN 147481.00 12. 6 12.0 CGreen Code Plaza 1 Ma Sik Road Fan Ling NT 136533.00 4. 10 3. 9 CKolour.Tsuen Wan I 68 Chung On Street Tsuen Wan NT 394258.00 22. 8 22. 8 CKolour.Tsuen Wan II 67-95 Market St Tsuen Wan NT 156369.00 28. 5 21.0 CKolour.Yuen Long 1 Kau Yuk Road Yuen Long NT 152948.00 24. 5 24. 5 CKowloon Building 555 Nathan Rd Yau Ma Tei KLN 113384.00 31. 4 19. 6 CManhattan Plaza 23 Sai Ching St Yuen Long NT 48358.00 30. 1 20. 2 CManulife Financial Centre 223-231 Wai Yip St Kwun Tong KLN 1248389.00 11. -
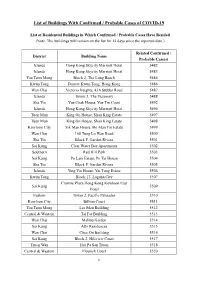
List of Buildings with Confirmed / Probable Cases of COVID-19
List of Buildings With Confirmed / Probable Cases of COVID-19 List of Residential Buildings in Which Confirmed / Probable Cases Have Resided (Note: The buildings will remain on the list for 14 days since the reported date.) Related Confirmed / District Building Name Probable Case(s) Islands Hong Kong Skycity Marriott Hotel 5482 Islands Hong Kong Skycity Marriott Hotel 5483 Yau Tsim Mong Block 2, The Long Beach 5484 Kwun Tong Dorsett Kwun Tong, Hong Kong 5486 Wan Chai Victoria Heights, 43A Stubbs Road 5487 Islands Tower 3, The Visionary 5488 Sha Tin Yue Chak House, Yue Tin Court 5492 Islands Hong Kong Skycity Marriott Hotel 5496 Tuen Mun King On House, Shan King Estate 5497 Tuen Mun King On House, Shan King Estate 5498 Kowloon City Sik Man House, Ho Man Tin Estate 5499 Wan Chai 168 Tung Lo Wan Road 5500 Sha Tin Block F, Garden Rivera 5501 Sai Kung Clear Water Bay Apartments 5502 Southern Red Hill Park 5503 Sai Kung Po Lam Estate, Po Tai House 5504 Sha Tin Block F, Garden Rivera 5505 Islands Ying Yat House, Yat Tung Estate 5506 Kwun Tong Block 17, Laguna City 5507 Crowne Plaza Hong Kong Kowloon East Sai Kung 5509 Hotel Eastern Tower 2, Pacific Palisades 5510 Kowloon City Billion Court 5511 Yau Tsim Mong Lee Man Building 5512 Central & Western Tai Fat Building 5513 Wan Chai Malibu Garden 5514 Sai Kung Alto Residences 5515 Wan Chai Chee On Building 5516 Sai Kung Block 2, Hillview Court 5517 Tsuen Wan Hoi Pa San Tsuen 5518 Central & Western Flourish Court 5520 1 Related Confirmed / District Building Name Probable Case(s) Wong Tai Sin Fu Tung House, Tung Tau Estate 5521 Yau Tsim Mong Tai Chuen Building, Cosmopolitan Estates 5523 Yau Tsim Mong Yan Hong Building 5524 Sha Tin Block 5, Royal Ascot 5525 Sha Tin Yiu Ping House, Yiu On Estate 5526 Sha Tin Block 5, Royal Ascot 5529 Wan Chai Block E, Beverly Hill 5530 Yau Tsim Mong Tower 1, The Harbourside 5531 Yuen Long Wah Choi House, Tin Wah Estate 5532 Yau Tsim Mong Lee Man Building 5533 Yau Tsim Mong Paradise Square 5534 Kowloon City Tower 3, K. -

香港物業管理公司協會有限公司the Hong Kong Association of Property Management Companies Limited
香港物業管理公司協會有限公司 The Hong Kong Association of Property Management Companies Limited 會員轄下物業資料 Date : 2016-01-08 Members Portfolios Property Registers 會員編號 F-0060/99 公司名稱: 冠威管理有限公司 Membership No.: Company Name: Goodwill Management Limited 總樓宇面積 單位面積 (平方呎) 類別 物業名稱及地點 物業地址 類別/座數 單位數目 Unit Size GFA 樓齡 管理年數 Type Properties Properties Address Type/No. of Blocks No. of Units Min/Max Sq. Ft. Age Yrs.Managed C AIA Tower 183 Electric Road North Point HK 515645.00 17. 8 17. 8 C Dawning Views Plaza 23 Yat Ming Rd Fanling NT 96365.00 16. 7 16. 7 C Fanling Centre Shopping Arcade 33 San Wan Road Fanling NT 151513.00 25. 1 25. 1 C FWD Financial Centre 308-320 Des Voeux Rd C HK 225851.00 21. 3 21. 3 C Golden Centre 188 Des Voeux Rd Central HK 156562.00 24. 10 24. 10 C Grand Waterfront Plaza 38 San Ma Tau Street Ma Tau Kok KLN 147481.00 9. 2 8. 8 C Green Code Plaza 1 Ma Sik Road Fan Ling NT 136533.00 1. 6 0. 5 C Kolour.Tsuen Wan I 68 Chung On Street Tsuen Wan NT 394258.00 19. 4 19. 4 C Kolour.Tsuen Wan II 67-95 Market St Tsuen Wan NT 156369.00 25. 1 17. 8 C Kolour.Yuen Long 1 Kau Yuk Road Yuen Long NT 152948.00 21. 1 21. 1 C Kowloon Building 555 Nathan Rd Yau Ma Tei KLN 113384.00 28.0 16. 2 C Manhattan Plaza 23 Sai Ching St Yuen Long NT 48358.00 26. -

Sai Wan Ho (Grand Promenade)
TRAFFIC ADVICE Service Adjustment of Cross Harbour Route No. 608 Kowloon City (Shing Tak Street) - Sai Wan Ho (Grand Promenade) Members of the public are advised that service of Cross Harbour Route No. 608 will be adjusted with effect from 2 December 2018 (Sunday). The service details after the adjustment are as follows: (i) Routeing: KOWLOON CITY (SHING TAK STREET) TO SAI WAN HO (GRAND PROMENADE): via Shing Tak Street, Fu Ning Street, Ma Tau Chung Road, Mok Cheo ng Street, To Kwa Wan Road, Shing Kai Road, Muk On Street, Muk Ning Street*, roundabout, Muk Ning Street*, Muk On Street, Shing Kai Road, Wang Chiu Road, Kai Cheung Road, Kai Fuk Road, Kwun Tong Bypass, Lei Yue Mun Road, Eastern Harbour Crossing, Island Ea stern Corridor, Man Hong Street, King's Road, Shau Kei Wan Road and Tai Hong Street. SAI WAN HO (GRAND PROMENADE) TO KOWLOON CITY (SHING TAK STREET): via Tai On Street, Shau Kei Wan Road, King's Road, Kornhill Road, King's Road, Healthy Street West, Tsat Tsz Mui Road, Tin Chiu Street, Java Road, Man Hong Street, Island Eastern Corridor, Eastern Harbour Crossing, Lei Yue Mun Road, Kwun Tong Bypass, Wang Chiu Road, Shing Kai Road, Muk On Street, Muk Ning Street*, roundabout, Muk Ning Street*, Muk On Street, Shing Kai Road, To Kwa Wan Road, Ma Tau Wai Road, San Lau Street, Chatham Road North, Ma Tau Wai Road, Ma Tau Chung Road, Ma Tau Kok Road and Shing Tak Street. (ii) Frequency and Operation Period: Mondays to Fridays (except Public Holidays): Depart from Kowloon City (Shing Tak Street): from 5:40 a.m. -

Group's Investments Distribution
GROUP’S INVESTMENTS DISTRIBUTION MAP Lo Wu CHINA Lok Ma Chau Sheung Shui Fanling 9 4 Tai Po Yuen Long NEW TERRITORIES 5 Shatin 8 Tsuen Wan 7 6 Tuen Mun Miramar Hotel & Investment KOWLOON Lai King Kowloon Tsing Yi Tong 4 3 4 Hong Kong Mong 2 International Airport Kok 1 Hunghom 3 2 3 2 3 42 Discovery Bay 1 2 Tung Chung Metro 1 Harbour View 1 Quarry 2 Central Bay Mui Wo LANTAU ISLAND 1 HONG KONG ISLAND Chai Wan 43-51A Tong Mi Road Investment Properties 1. Eva Court 36 MacDonnell Road, Mid-levels 2. Hollywood Plaza 610 Nathan Road, Mongkok 3. Kowloon Building 555 Nathan Road, Mongkok 4. Well Tech Centre First to Fifteenth Floors and Twentieth to Twenty-Ninth Floors, 9 Pat Tat Street, San Po Kong 5. Shatin Centre 2-16 Wang Pok Street, Shatin 6. City Landmark II 145-165 Castle Peak Road, Tsuen Wan 7. The Trend Plaza Heung Sze Wui Road, Tuen Mun 8. Block C Hang Wai Industrial Centre Pui To Road/Kin On Street/ Kin Wing Street/Kin Tai Street, Tuen Mun 9. Fanling Centre 33 San Wan Road, Fanling Hotel Investment and Operation 1. Newton Hotel Hong Kong 200-218 Electric Road, North Point 2. Newton Hotel Kowloon 58-66 Boundary Street, Mongkok Ma On Shan The Hong Kong and China Gas Company Limited* 1. International Finance Centre 1 Harbour View Street/8 Finance Street, Central 2. Grand Promenade 38 Tai Hong Street, Sai Wan Ho 3. The Grand Waterfront San Ma Tau Street, South Eastern Kowloon 4. -

TKO Bus Routes 2021-22 (Tentative)
2021 - 2022 [FOR REFERENCE ONLY] FIS TKO Campus (Return Schedules for Primary Students) *Bus routes and stops are subjected to change based on number of applicants **All schedules are depending on actual traffic conditions Bus 1B HK Parkview, Happy Valley Return Point RETURN TIME TKO Campus (approximate time +/- 10min) 2:30 1 80 Kennedy Road 3:00 2 3 Repulse Bay Road 3:12 3 HK Parkview (Hotel) 3:14 4 Green Lane (Wendy Apartments) 3:20 5 Wong Nai Chung Road: near Market Place 3:23 Bus 2 Midlevel Return Point RETURN TIME TKO Campus (approximate time +/- 10min) 2:30 1 11 Maganize Gap Road 3:00 2 1, 3, 12 Tregunter Path 3:03 3 23 Old Peak Road 3:06 4 9 Old Peak Road 3:08 5 8 Kotewall Road 3:15 6 6 Park Road 3:20 7 80-82 Bonham Road 3:25 8 High Street / Bonham Road 3:28 Bus 3A Kornhill, Fortress Hill, Tai Hang Return Point RETURN TIME TKO Campus (approximate time +/- 10min) 2:30 1 Kornhill (Block D, K) 2:55 2 Mount Parker Residences (front gate) 2:58 3 The Orchards (before traffic light) 3:03 4 Nam Fung Sun Chuen Block 4 3:04 5 238 King's Road (MacDonald) 3:12 6 City Garden Hotel (on Electric Road) 3:15 7 111 Mount Butler Road 3:25 8 70 Tai Hang Road 3:30 Page 1 of 5 Bus 3B North Point, Taikoo, Sai Wan Ho Return Point RETURN TIME TKO Campus (approximate time +/- 5min) 2:30 1 Kwun Tong Police Station (bus stop) 2:40 2 Grand Promenade 2:50 3 Taikoo Shing (HSBC) 2:57 4 Healthy Road West (across of Yoshinoya) 3:03 5 35 Cloud View Road 3:10 6 26 -32 Tin Hau Temple Road (Fly Dragon Terrace) 3:12 7 6 Tin Hau Temple Road 3:12 8 Hing Fat Street (Victoria -

M / SP / 14 / 152 PLAN No
24 150 ES T23 22 W 21 R D 2 9 20 A R D 3 D W m– CE E P R IN 11 £ß l D è 5 m– Choi Fook Estate 9 12 100 [˘ Choi Ying 7 KAI LAI ROAD WANG CHIU ROAD Estate 7 £û§ CHOI WAN ROAD 2.8.5 7 D 15 E⁄sW˘ 6 h Kowloon Bay Sports Ground m±³ Q ¶¶ 3 100 ¶ 4 13 m±ø I HEI o±_Ä O RO Shun Tin Estate CH AD Tak Bo Garden 2 4 50 15 H ¶~ m 8 »§ú m±ø 50 KAI LOK STREET » Choi Ha Estate 8 2.4.6 2 SHUN LEE TSUEN ROAD †»U§˜ 20 13 100 KAI SHUN ROAD Hong Kong OLYMPIC AVENUE 50 £ûH Auxiliary Police 14 EMSD q„u 6 6 MA TAU CHUNG ROAD 100 5 2.9.2 KAI CHEUNG ROAD @¥B ë C 5 150 H N –» 19 O I u ß⁄Y l H 40 l a ^²j¤ A ¤Y h 18 8 R 2 O 9 A D 30 E¤s 17 ıƒ KOWLOON BAY 2.9.1 [˘¶W⁄t {Á³ ]¡³¦\»t JORDAN VALLEY Kwun Tong High Level ”§‹ 39 KWUN TONG BYPASS Service Reservoir Garden LAM HING STREET 11 50 £ûw¼ KAI TAK TUNNEL (Service Reservoir under) WANG KWUN ROAD Œ»ifi Amoy Gardens 2 2.8.0 WAI YIP STREET º O D International Trade & ıƒ·ƒ¤ Exhibition Centre WANG CHIN STREET 3 22 Jordan Valley Swimming Pool 150 ⁄h »§ »§ 14 Bus Depot 20 21 100 _¥ ƶ³ w…˜ Sky Tower Telford Gardens 4 »§õ 54 6 »§} ß⁄Y⁄ 23 {` …fi WANG KWONG ROAD 12 150 LAM WAH STREET Lok Nga Court ⁄t 1 5 WANG KEE STREET SUNG WONG TOI ROAD D – »§i ¶ 25 26 C 3 H PAK TAI ST U KOWLOON CITY ROAD Lower Ngau Tau Kok Estate N ”« 2 LAM LOK ST W Fukien A Secondary School H »§a 4 wƒ R ¤Y {` 7 MOK CHEONG STREET O 52 A D 5 »§i ON WAH ST 6 100 49 100 7 `±® … On Kay WANG HOI ROAD 61 2.4.1 8 Lok Wah North Estate 9 SHEUNG YUET ROAD Court 10 24 90 KWUN TONG ROAD WANG CHIU ROAD 11 WANG TUNG ST 8 9 57 12 MA TAU KOK ROAD û¤Y »§· Yªaº 13 60 -

DDC Location Plan Apr-2015 Quarry Bay MTR Station Exit a Nam Cheong MTR Station Exit Training / Day Off Training / Day
WWF - DDC Location Plan Apr-2015 Mon Tue Wed Thu Fri Sat Sun 1 2 3 4 5 Team A Quarry Bay MTR Station Exit A Nam Cheong MTR Station Exit Training / Day Off Training / Day Off Training / Day Off Cheung Sha Wan Road, Lai Chi Kok Team B Yun Ping Road,Causeway Bay Training / Day Off Training / Day Off Training / Day Off (near Cheung Sha Wan Plaza) Wan Chai Pedestrian Footbridge Great George Street, Team C Citimall, Yuen Long Great George Street, Causeway Bay Great George Street, Causeway Bay (near Immigration Tower) Causeway Bay Wan Chai Pedestrian Footbridge Kornhill Road, Quarry Bay Team D Mei Foo MTR Station Exit A Mei Foo MTR Station Exit A Mei Foo MTR Station Exit A (near Immigration Tower) (near Jusco) Kornhill Road, Quarry Bay Tat Tung Road, Tung Chung Team E Tai Wai MTR Station Exit C Tai Wai MTR Station Exit C Tai Wai MTR Station Exit C (near Jusco) (near Bus Terminal) Tat Tung Road, Tung Chung Team F Long Ping MTR Station Exit B2 Long Ping MTR Station Exit B2 Long Ping MTR Station Exit B2 (near Bus Terminal) 6 7 8 9 10 11 12 Nathan Road, Prince Edward Ngau Tau Kok Road, Ngau Tau Kok Nathan Road, Tsim Sha Tsui Team A Training / Day Off Training / Day Off Great George Street, Causeway Bay (near Pioneer Centre) (near Municipal Services Building) (near St. Andrew Church) Kwai Fu Road, Kwai Chung Wai Man Road, Sai Kung Team B Training / Day Off Training / Day Off Kennedy Town MTR Station Exit C Quarry Bay MTR Station Exit A (near Kwai Chung Plaza) (near Bus Terminal) Connaught Place, Central Connaught Place, Central Connaught Place, Central -

Restaurant List
Restaurant List (updated 1 July 2020) Island Cafeholic Shop No.23, Ground Floor, Fu Tung Plaza, Fu Tung Estate, 6 Fu Tung Street, Tung Chung First Korean Restaurant Shop 102B, 1/F, Block A, D’Deck, Discovery Bay, Lantau Island Grand Kitchen Shop G10-101, G/F, JoysMark Shopping Centre, Mung Tung Estate, Tung Chung Gyu-Kaku Jinan-Bou Shop 706, 7th Floor, Citygate Outlets, Tung Chung HANNOSUKE (Tung Chung Citygate Outlets) Shop 101A, 1st Floor, Citygate, 18-20 Tat Tung Road, Tung Chung, Lantau Hung Fook Tong Shop No. 32, Ground Floor, Yat Tung Shopping Centre, Yat Tung Estate, 8 Yat Tung Street, Tung Chung Island Café Shop 105A, 1/F, Block A, D’Deck, Discovery Bay, Lantau Island Itamomo Shop No.2, G/F, Ying Tung Shopping Centre, Ying Tung Estate, 1 Ying Tung Road, Lantau Island, Tung Chung KYO WATAMI (Tung Chung Citygate Outlets) Shop B13, B1/F, Citygate Outlets, 20 Tat Tung Road, Tung Chung, Lantau Island Moon Lok Chiu Chow Unit G22, G/F, Citygate, 20 Tat Tung Road, Tung Chung, Lantau Island Mun Tung Café Shop 11, G/F, JoysMark Shopping Centre, Mun Tung Estate, Tung Chung Paradise Dynasty Shop 326A, 3/F, Citygate, 18-20 Tat Tung Road, Tung Chung, Lantau Island Shanghai Breeze Shop 104A, 1/F, Block A, D’Deck, Discovery Bay, Lantau Island The Sixties Restaurant No. 34, Ground Floor, Commercial Centre 2, Yat Tung Estate, 8 Yat Tung Street, Tung Chung 十足風味 Shop N, G/F, Seaview Crescent, Tung Chung Waterfront Road, Tung Chung Kowloon City Yu Mai SHOP 6B G/F, Amazing World, 121 Baker Street, Site 1, Whampoa Garden, Hung Hom CAFÉ ABERDEEN Shop Nos. -

Results Tertiary Education Student Group Champion: FUNG Hon
Water Conservation Design Competition - Results Tertiary Education Student Group Champion : FUNG Hon Chung, WONG Wing Yee First Runner -up : WONG Sai Wai Second Runner -up : HUANG Sheng Cheng Merit Awards : 1) WONG Sze Man, LUK Wing Ping, PANG Chiu Man, LAW Che uk Hei, WONG Chung Yin, WONG Yip Sun, CHAN Wai Kwan 2) CHEUNG Kin Sung, CHE UNG Chi Hon, CHEUNG Lee Ni, CHEUNG Wing Tak, LO Sing Fai, CHAN Wing Yuen 3) LAM Suet Yu, WONG Shu Wan Catering Services Group Champion : Winkey Development Limited / Treasure Lake Golden Banquet Restaurant First Runner -up : Med Star Café Second Runner -up : LH Group Merit Award : JW Marriott Hotel Hong Kong Property Management Group Champion : MTR Corporation Limited / The Palazzo First Runner -up : ARA Asset Management (Prosperity) L imited / Prosperity Place Second Runner -up : MTR Corporation Limited / The Grandiose Merit Awards : 1) Henderson Land Group Subsidiary Well Born Real Estate Management Limited / The Sherwood 2) Henderson Land Group Subsidiary Well Born Real Estate Manageme nt Limited / Grand Waterfront 3) Goodwell Property Management L imited / Sceneway Garden Commendation : 1) Henderson Land Group Subsidiary Well Born Real Estate Management Limited / The Beverly Hills 2) The Incorporated Owners of Garden Vista / Garden Vista 3) Goodwell Property Management L imited / Vista Paradiso 4) Hong Kong Housing Authority Lok Man Sun Chuen Estate O ffice / Lok Man Sun Chuen 5) Hong Kong Housing Authority The Pinnacle Management Office / The Pinnacle. -

Corporate 1 Template
Vigers Hong Kong Property Index Series • As a complement to the existing property information related to the Hong Kong property market • To better inform public of the ever-changing residential market as Vigers has selected residential districts or areas which will be impacted by the Objectives territories’ infrastructure project, i.e. the MTR network expansion • To continually get updates from the property market 2 Hedonic model of price measurement Assumption Asset’s value can be derived from the value of its different characteristics Home Price Dependence on the values that buyers have placed on both qualitative and quantitative attributes Hedonic Estimation of the implicit market value of each Regression attributes of a property by comparing sample home prices with their associated characteristics, on a monthly basis Logarithm of transaction price will be used as independent variable for the regression model, whilst logarithm of dependent variables, such as building’s age, floor numbers, floor areas, and regional, district and estate building names will be selected in the model as controls for quality mix, apart from the time dummy variables (which are the most important part of the model), being employed. Methodology 3 The “Vigers Hong Kong Property Price Index Series” provides a perspective to understand movements in the Hong Kong private housing prices, based on the types or locations of properties. By applying the “Hedonic Regression Model”, the Index Series calculate property price changes relative to a base period at January 2017 (Level 100). Every published index represents an average of its latest six individual monthly indexes. All property attributes such as Building Age, Floor Number, Net Floor Size and Estates / Districts used in these calculations are consistent. -

Office Address of the Labour Relations Division
If you wish to make enquiries or complaints or lodge claims on matters related to the Employment Ordinance, the Minimum Wage Ordinance or contracts of employment with the Labour Department, please approach, according to your place of work, the nearby branch office of the Labour Relations Division for assistance. Office address Areas covered Labour Relations Division (Hong Kong East) (Eastern side of Arsenal Street), HK Arts Centre, Wan Chai, Causeway Bay, 12/F, 14 Taikoo Wan Road, Taikoo Shing, Happy Valley, Tin Hau, Fortress Hill, North Point, Taikoo Place, Quarry Bay, Hong Kong. Shau Ki Wan, Chai Wan, Tai Tam, Stanley, Repulse Bay, Chung Hum Kok, South Bay, Deep Water Bay (east), Shek O and Po Toi Island. Labour Relations Division (Hong Kong West) (Western side of Arsenal Street including Police Headquarters), HK Academy 3/F, Western Magistracy Building, of Performing Arts, Fenwick Pier, Admiralty, Central District, Sheung Wan, 2A Pok Fu Lam Road, The Peak, Sai Ying Pun, Kennedy Town, Cyberport, Residence Bel-air, Hong Kong. Aberdeen, Wong Chuk Hang, Deep Water Bay (west), Peng Chau, Cheung Chau, Lamma Island, Shek Kwu Chau, Hei Ling Chau, Siu A Chau, Tai A Chau, Tung Lung Chau, Discovery Bay and Mui Wo of Lantau Island. Labour Relations Division (Kowloon East) To Kwa Wan, Ma Tau Wai, Hung Hom, Ho Man Tin, Kowloon City, UGF, Trade and Industry Tower, Kowloon Tong (eastern side of Waterloo Road), Wang Tau Hom, San Po 3 Concorde Road, Kowloon. Kong, Wong Tai Sin, Tsz Wan Shan, Diamond Hill, Choi Hung Estate, Ngau Chi Wan and Kowloon Bay (including Telford Gardens and Richland Gardens).