DOCSLIB.ORG

Snubber Circuits

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Snubber Circuits Lecture Notes Snubber Circuits William P. Robbins Dept. of Electrical and Computer Engineering University of Minnesota Outline A. Overview of Snubber Circuits B. Diode Snubbers C. Turn-off Snubbers D. Overvoltage Snubbers E. Turn-on Snubbers F. Thyristor Snubbers Snubbers -1 1 W.P. Robbins Overview of Snubber Circuits for Hard-Switched Converters Function: Protect semiconductor devices by: Types of Snubber Circuits • Limiting device voltages during turn-off transients 1. Unpolarized series R-C snubbers • Used to protect diodes and thyristors • Limiting device currents during turn-on transients 2. Polarized R-C snubbers • Limiting the rate-of-rise (di/dt) of currents through • Used as turn-off snubbers to shape the turn-on the semiconductor device at device turn-on switching trajectory of controlled switches. • Used as overvoltage snubbers to clamp voltages applied to controlled switches to safe values. • Limiting the rate-of-rise (dv/dt) of voltages across • Limit dv/dt during device turn-off the semiconductor device at device turn-off 3. Polarized L-R snubbers • Shaping the switching trajectory of the device as it • Used as turn-on snubbers to shape the turn-off turns on/off switching trajectory of controlled switches. • Limit di/dt during device turn-on Snubbers - 2 W.P. Robbins Need for Diode Snubber Circuit di Df Vd = d t L L σ + σ R Io s I t o i Df (t) D I Vd f Cs rr - Sw v (t) t Df Vd • Lσ = stray inductance • S w closes at t = 0 • Diode voltage di L σ without snubber Lσ • Rs - Cs = snubber circuit d t diLσ • Diode breakdown if V + L > BV d σ dt BD Snubbers - 3 W.P. Robbins Equivalent Circuits for Diode Snubber L σ • Simplified snubber - the capacitive snubber + R s L Diode cathode σ Vd snap-off anode - + + v Vd Cs Cs - - i Df t • Rs = 0 • Worst case assumption- • v = -v diode snaps off instantaneously Cs Df at end of diode recovery 2 d vCs vCs Vd • Governing equation - + = dt2 LσCs LσCs + + • Boundary conditions - vCs(0 ) = 0 and iLσ(0 ) = Irr Snubbers - 4 W.P. Robbins Performance of Capacitive Snubber Cbase • vCs(t) = Vd - Vd cos(ωot) + Vd sin(ωot) Cs 2 1 Irr • ω = ; C = L o base σ V LσCs d Cbase • Vcs,max = Vd 1 + 1 + Cs 5 4 V 3 Cs,max Vd 2 1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 C base C Snubbers - 5 s 5 W.P. Robbins Effect of Adding Snubber Resistance Snubber Equivalent Circuit Lσ i(t) d2i di i • Governing equation L + R + = 0 + - σ 2 s dt C R s dt s V v (t) d Df • Boundary conditions + V - I R Cs + di(0 ) d rr s - + i(0 ) = Irr and = dt Lσ Diode voltage as a function of time Vdf e-αt (t) = - 1 - sin(ω t - φ + ζ) ; R ≤ 2 R Vd η cos(φ) a s b R 2 s 1 -1 (2-x) η ωa = ωo 1- (α/ ωo) ; α = 2 L ; ωo = ; φ = tan σ LσCs 4 - ηx2 C R V L [I ]2 s s d σ rr -1 η = C ; x = R ; Rb = I ; Cb = 2 ; ζ = tan (α/ωa) b b rr Vd Snubbers - 6 W.P. Robbins Performance of R-C Snubber 3 • At t = tm vDf(t) = Vmax R s,opt C s = Cbase = 1.3 -1 R tan (ωa/α) φ - ξ base • t = ω + ω ≥ 0 m a a 2 V Vmax max • = 1 + 1 + -1 - x exp(- t ) η α m V Vd d Cs Rs 1 • η = and x = Cbase Rbase R s I rr 2 V Ls Irr Vd d • C = and R = base 2 base I 0 Vd rr 0 1 R s 2 R base Snubbers - 7 W.P. Robbins Diode Snubber Design Nomogram Wtot 2 3 L s I rr /2 WR 2 L s I rr /2 0 2 0 V 0 max for R = R V s s,opt 0 d 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 R s,op R base 0 0 1 2 3 Snubbers - 8 C / C s base 8 W.P. Robbins Need for Snubbers with Controlled Switches Step-down converter Switch current and voltage waveforms di Lσ L dt 1 L 2 I rr I o i sw V d di i Lσ V I sw + I o dt d o vsw S w L 3 - vsw t t t t t 3 t 5 6 o 1 4 • = stray inductances L1 , L 2 , L 3 Switching trajectory of switch • = Lσ L1 + L 2 + L3 idealized i sw switching t loci t 6 5 t turn-off o • Overvoltage at turn-off t1 due to stray inductance turn-on • Overcurrent at turn-on due to diode reverse recovery t 4 t 3 vsw Vd Snubbers - 9 W.P. Robbins Turn-off Snubber for Controlled Switches Turn-off D snubber i f I + D o F V d Ds Step-down converter with turn-off snubber S R s w i - C C s s Equivalent circuit during switch turn -off. I o D f • Simplifying assumptions 1. No stray inductance. V d I - i o sw 2. isw(t) = Io(1 - t/tfi) i sw C s 3. isw(t) uneffected by snubber circuit. Snubbers - 10 W.P. Robbins Turn-off Snubber Operation 2 Iot I o t • Capacitor voltage and current for 0 < t < t i (t) = and v (t) = fi Cs t Cs 2C t fi s fi Iotfi • For Cs = Cs1, vCs = Vd at t = tfi yielding Cs1 = 2Vd Circuit waveforms for varying values of Cs i i i sw sw sw I o i D i i f Df Df t t fi t fi fi i C s V d v Cs Snubbers - 11 Cs < C Cs = Cs1 C s > C s1 s W.P. Robbins 1 Benefits of Snubber Resistance at Switch Turn-on vsw t D I I rr f o o • D shorts out R R s s i I s D rr during Sw turn-off. f V d V • During Sw turn-on, d S I w Ds D reverse-biased and i o s sw R s C s Cs discharges thru Rs. I rr • Turn-on with Rs > 0 discharge t rr • Energy stored on Cs dissipated of C s in Rs rather than in Sw. • Turn-on with Rs = 0 vsw • Voltage fall time kept quite short. • Energy stored on Cs dissipated V I o d in Sw. i sw t t ri 2 • Extra energy dissipation in Sw 0 because of lengthened voltage t ri + t rr fall time. Snubbers - 12 W.P. Robbins Effect of Turn-off Snubber Capacitance 1 Energy dissipation W / total Wbase W 0.8 WR = dissipation in resistor 0.6 WT = dissipation in W / W R base 0.4 switch Sw WT / Wbase W 0.2 Iotfi Cs1 = 2Vd 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 Wtotal = WR + WT Cs / Cs1 i sw Wbase = 0.5 VdIotfi I o Cs < Cs1 RBSOA Switching trajectory Cs = Cs1 Cs > Cs1 V v d sw Snubbers - 13 W.P. Robbins Turn-off Snubber Design Procedure Selection of Cs • Minimize energy dissipation (WT) in BJT at turn-on • Minimize WR + WT • Keep switching locus within RBSOA Snubber recovery time (BJT in on-state) • Reasonable value is Cs = Cs1 • Capacitor voltage = Vd exp(-t/RsCs) • Time for vCs to drop to 0.1Vd is 2.3 RsCs • BJT must remain on for a time of 2.3 R C Selection of Rs s s Vd • Limit i (0+) = < I cap Rs rr Vd • Usually designer specifies I < 0.2 I so = 0.2 I rr o Rs o Snubbers - 14 W.P. Robbins Overvoltage Snubber L σ kV d + i D R s f I o ov w V d I V o d Sw Dov - Cov v s w t o fi • Step-down converter with overvoltage snubber comprised of Dov, Cov, and Rov. • Switch Sw waveforms without overvoltage snubber • t = switch current fall time ; kV = overvoltage on S • Overvoltage snubber limits fi d w overvoltage (due to stray diLσ Io Inductance) across Sw as it • kVd = Lσ = Lσ turns off. dt tfi kVdtfi • Lσ = Io Snubbers - 15 W.P. Robbins Operation of Overvoltage Snubber π LσCov i • D on for 0 < t < Lσ ov 2 L + σ R π LσCov Dov ov • t << fi 2 V d + C v - ov Cov - • Dov,Cov provide alternate path for inductor current as Sw turns off. • Switch current can fall to zero much faster than Ls current. • Df forced to be on (approximating a short ckt) by Io after Swis off. Snubbers - 16 W.P. Robbins Overvoltage Snubber Design Lο • Limit v to 0.1V = Io sw,max d Cov kVd tfi • Using L = in above equation yields Io € 2 kVdtfiIo 100k tfi Io • C = = ov 2 V Io(0.1Vd) d tfiIo • Cov = 200 k Cs1 where Cs1 = which is used 2Vd in turn-off snubber • Choose Rov so that the transient recovery of Cov is critically damped so that ringing is minimized. For a critically damped ω L L 1 o σ = σ circuit Q = 1 = . Rov Cov Rov 0.1Vd • Rov = Io € • Check that the recovery time of Cov (2.3L /Rov) is less € than off-time duration, toff, of the switch Sw.
Load more

Recommended publications
  • Snubber Considerations for IGBT Applications
    Snubber Considerations for IGBT Applications by Yi Zhang, Saed Sobhani, Rahul Chokhawala International Rectifier Applications Engineering 233 Kansas St., El Segundo, CA, 90245 USA Abstract - Snubber circuits can be used to protect fast Note that the fault current transients are more switching IGBTs from turn-on and turn-off voltage effectively protected by considerably slowing the rate transients. Snubbers are available in various of fall of fault current. Fault current turn-off protection configurations and a clear understanding of their through electronic gate control is convered in detail operation is necessary to make the appropriate elsewhere[1]. selection. This paper will discuss pros and cons of these circuits. Decoupling capacitors, RCD voltage Decoupling Capacitors clamp circuit, RCD charge-discharge snubbers are As mentioned earlier, the magnitude of transient voltage included in the discussion. depends on the trapped energy in the circuit stray inductance, also call “DC loop” inductance LS. As a Introduction preventive measure, steps should be taken to improve When a power device is abruptly turned off, trapped the circuit layout. Usage of laminated copper plates, energy in the circuit stray inductance is dissipated in minimizing the size of the “DC loop” and choosing the switching device, causing a voltage overshoot source capacitance with inherently low self inductance across the device. The magnitude of this transient are ways to lower stray inductance [2]. Decoupling voltage is proportional to the amount of stray capacitors, connected across the module’s bus inductance and the rate of fall or turn-off current. The terminals, as shown in Fig.1a, are found to be useful situation is at its worst for fast switching IGBT for low/medium current applications.
    [Show full text]
  • AN1048/D RC Snubber Networks for Thyristor Power Control
    AN1048/D RC Snubber Networks For Thyristor Power Control and Littelfuse.com Transient Suppression By George Templeton APPLICATION NOTE Thyristor Applications Engineer INTRODUCTION Edited and Updated RC networks are used to control voltage transients that ǒdVǓ DEVICE PHYSICS could falsely turn-on a thyristor. These networks are called dt s snubbers. Static dV turn-on is a consequence of the Miller effect The simple snubber consists of a series resistor and dt capacitor placed around the thyristor. These components and regeneration (Figure 1). A change in voltage across the along with the load inductance form a series CRL circuit. junction capacitance induces a current through it. This cur- Snubber theory follows from the solution of the circuit’s rent is proportional to the rate of voltage change ǒdVǓ . It differential equation. dt Many RC combinations are capable of providing accept- triggers the device on when it becomes large enough to able performance. However, improperly used snubbers can raise the sum of the NPN and PNP transistor alphas to unity. cause unreliable circuit operation and damage to the semi- conductor device. A Both turn-on and turn-off protection may be necessary A for reliability. Sometimes the thyristor must function with a I IA BP PE range of load values. The type of thyristors used, circuit V PNP configuration, and load characteristics are influential. I CJ I I 1 P J CP NB CJ Snubber design involves compromises. They include N C C I J CN I2 dv I G P cost, voltage rate, peak voltage, and turn-on stress. Practi- J dt B cal solutions depend on device and circuit physics.
    [Show full text]
  • Minimizing Switching Ringing at TPS53355 and TPS53353 Family Devices
    Application Report SLUA831A–July 2017–Revised November 2018 Minimizing Switching Ringing at TPS53355 and TPS53353 Family Devices Benyam Gebru ABSTRACT The system reliability of a high efficiency DC/DC converter with a fast slew rate is improved when switch node ringing is reduced. This document describes switching ringing reduction methods and lab bench test results with the 30-A TPS53355, and also applies to the pin compatible 20-A TPS53353. Both devices are well-suite for rack server, single board computer, and hardware accelerator applications that benefit from the fast transient response time of D-CAPTM control, or when multi-layer ceramic capacitors are undesirable for the output filter. Contents 1 Introduction ................................................................................................................... 2 2 Proper Measurement Method of Switch Ringing ........................................................................ 2 3 Minimize the Switch Ringing by Adding RC Snubber and Bootstrap Circuit......................................... 5 4 Practical Design.............................................................................................................. 8 5 Adding Bootstrap Resistor ................................................................................................ 11 6 Effects of Snubber on the Efficiency Performance .................................................................... 12 7 Summary ...................................................................................................................
    [Show full text]
  • Single and Dual RC Snubbers
    RC Snubbers Single and dual RC snubbers Description: A range of RC snubbers suitable for a broad range of circuit protection applications. The RC snubbers are mounted in a potted box with 6.3mm push on tabs for easy connection to the circuit. The devices have 80mm fixing centers so can be easily mounted alongside industry standard thyristor and diode modules. The range of RC snubbers are suitable for 50Hz/60Hz operation with resistive loads. Images shown are computer generated, for accurate package information please see product drawing Product Highlights Applications 80mm fixing centres Thyristor protection in AC and DC circuits Compact package Diode Protection 440Vrms rating (690Vrms available upon request) Output filters Component Data: Product Reference Maximum varistor energy (J) l voltage 10% 10% - - 10/1000us 2ms Configuration Resistance Value (Ohms) +/ Max. Power Dissipation (W) Capacitance Value (uf) +/ Maximum working voltage (Vrms) Dimension figure. Circuit configuration Varistor nomina (Vrms) ECLRC440 Single RC 56 10 0.22 440 N/A 1 A ECLRC440-2 Dual RC 56 10 0.22 440 N/A 2 B Humidity max. 50% RH @ 35 C / 90% RH @ 20 C Pollution degree: III Isolation: 2500Vrms / 1min Operation temperature: -25C to 80C Mounting position: Any Approx weight: 70grms (single) / 76grms (Dual) (1) The voltages shown are for general phase control applications in W1C circuits. (2) Typical voltage for general purpose rectifier circuits ATTENTION: for continuous operation near to 90 deg phase angle a larger power loss will occur, please consult the factory in these circumstances to see if the device is suitable for the application [email protected] Data can be changed without notice.
    [Show full text]
  • Lossless Active Snubber for Half-Bridge Output Rectifiers
    Europaisches Patentamt 19 European Patent Office Office europeen des brevets © Publication number: 0 614 267 A1 12 EUROPEAN PATENT APPLICATION (2j) Application number : 94301445.6 6i) Int. CI.5 : H02M 7/06 (22) Date of filing : 01.03.94 (§) Priority : 05.03.93 US 27031 @ Inventor : Tsai, Fu Sheng 105 Bartlett Street @ Date of publication of application : Northboro, Massachusetts 01532 (US) 07.09.94 Bulletin 94/36 Inventor : Dhaval, Dalai B. 70-9 Commons Drive Shrewsbury, Massachusetts 01545 (US) @ Designated Contracting States : DE FR GB IT (74) Representative : Goodman, Christopher et al Eric Potter & Clarkson © Applicant : DIGITAL EQUIPMENT St. Mary's Court CORPORATION St. Mary's Gate 146 Main Street Nottingham NG1 1LE (GB) Maynard, Massachusetts 01745 (US) @) Lossless active snubber for half-bridge output rectifiers. (57) A bridge-type primary switching circuit (12) is represented by a pulsed voltage source (VSW). The primary switched waveform is transformed to secondary circuit (14) using a transformer (T1) with the required turns ratio N and a cen- ter-tapped secondary winding (16). Half-bridge rectifier (18) formed by diodes (DR1) and (DR2) rectifies the secondary waveform and feeds the waveform through a low-pass filter (LF) and (CF) to obtain the desired DC output voltage. The snubber circuit (20) is represented by switch-diode-capacitor combinations (SA- DS1-CS1) and (SB-DS2-CS2) across each rec- tifier (DR1) and (DR2). Capacitances (CS1) and (CS2) are selected large enough such that their voltages remain essentially constant during a switching cycle. The controlled switches (SA) and (SB) are turned ON with a specific delay after the primary voltage reaches a magnitude close to the input voltage in order to allow the rectifier diodes (DR1) and (DR2) to be commu- tated.
    [Show full text]
  • SNUBBER Circuit
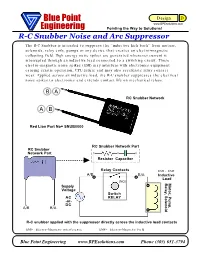
    Blue Point Design D www.BPEsolutions.com Engineering Pointing the Way to Solutions! R-C Snubber Noise and Arc Suppressor The R-C Snubber is intended to suppress the “inductive kick back” from motors, solenoids, relay coils, pumps or any device that creates an electro-magnetic collapsing field. High energy noise spikes are generated whenever current is interrupted through an inductive load connected to a switching circuit. These electro-magnetic noise spikes (EMI) may interfere with electronics equipment causing erratic operation, CPU failure and may also accelerate relay contact wear. Applied across an inductive load, the R-C snubber suppresses the electrical noise spikes to electronics and extends contact life on mechanical relays. B A RC Snubber Network A B Red Lion Part No= SNUB0000 RC Snubber Network Part RC Snubber Network Part Resistor Capacitor Relay Contacts EMI - EMF A/B B/A Inductive Load (NO) Relay, Solenoid Motor, Pump, Supply Voltage Switch AC RELAY -or- DC A/B B/A R-C snubber applied with the suppressor directly across the inductive load contacts EMI= Electro-Magnetic interference EMF= Electro-Magnetic Field Blue Point Engineering www.BPEsolutions.com Phone (303) 651-3794 Relay, Solenoid Motor, Pump, Blue Point Design D www.BPEsolutions.com Engineering Pointing the Way to Solutions! R-C Snubber Noise and Arc Suppressor APPLICATION The inductive load suppressors are effective in both AC and DC Power circuits Preferred Application Method R-C snubber should be applied with the inductive load suppressor directly across the inductive
    [Show full text]
  • RC Snubber Circuits
    Snubber Circuits For Power Electronics Rudy Severns 1 2 Snubber Circuits For Power Electronics Rudy Severns 3 Copyright © 2008 Rudolf Severns All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, mechanical, photo-copying, recording or otherwise, without prior written permission of Rudolf Severns. Legal notice: Great effort has been made to make the material presented in this book as accurate as possible. However, the author and publisher assume no responsibility or liability whatsoever on behalf of any Purchaser or Reader of these materials. It is the responsibility of the user to exercise good engineering judgment when using this material. A note from the author. Preparing a book like this takes well over 1000 hours of effort and a substantial investment by the author and publisher. Hopefully, this book will prove to be a useful contribution to the power electronics art. When such books are successful and provide some reasonable return to their authors, there is motivation to write more such books on other important subjects. The result is of benefit to all in our profession. Honesty is a fundamental requirement for any professional engineer and is expected of those in the profession or training for it. Your help is requested in not making copies of this work and distributing it to others or in accepting any such copy. 4 Table of contents PREFACE 7 ACKNOWLEDGEMENT 11 CHAPTER 1 13 An Overview Of Snubbers 13 What is a snubber? 21 Classifying snubbers
    [Show full text]
  • Power Stage Designer User's Guide (Rev. A)
    User's Guide SLVUBB4A–November 2017–Revised February 2018 Power Stage Designer™ Power Stage Designer™ is a Java® based tool that helps engineers speed up their power supply designs as it calculates voltages and currents of 20 topologies according to the user’s inputs. Additionally, Power Stage Designer contains a Bode plotting tool and a helpful toolbox with various functions for power supply design. This document describes how the different features of Power Stage Designer can be used and also explains the calculations behind these functions (for version 4 and higher). Contents 1 Topologies Window.......................................................................................................... 2 2 FET Losses Calculator ...................................................................................................... 4 3 Capacitor Current Sharing Calculator..................................................................................... 5 4 AC/DC Bulk Capacitor Calculator.......................................................................................... 7 5 RCD-Snubber Calculator for Flyback Converters ....................................................................... 8 6 RC-Snubber Calculator ..................................................................................................... 9 7 Output Voltage Resistor Divider.......................................................................................... 10 8 Dynamic Analog Output Voltage Scaling...............................................................................
    [Show full text]
  • Design of a Snubber Circuit for Low Voltage DC Solid-State Circuit Breakers
    This is a repository copy of Design of a snubber circuit for low voltage DC solid-state circuit breakers. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/171322/ Version: Published Version Article: Wang, Z. and Madathil, S. orcid.org/0000-0001-6832-1300 (2021) Design of a snubber circuit for low voltage DC solid-state circuit breakers. IET Power Electronics. ISSN 1755- 4535 https://doi.org/10.1049/pel2.12092 Reuse This article is distributed under the terms of the Creative Commons Attribution (CC BY) licence. This licence allows you to distribute, remix, tweak, and build upon the work, even commercially, as long as you credit the authors for the original work. More information and the full terms of the licence here: https://creativecommons.org/licenses/ Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ Received: 13 November 2020 Revised: 26 January 2021 Accepted: 15 February 2021 IET Power Electronics DOI: 10.1049/pel2.12092 ORIGINAL RESEARCH PAPER Design of a snubber circuit for low voltage DC solid-state circuit breakers Zhongying Wang Ekkanath Madathil Sankara Narayanan Department of Electronic and Electrical Abstract Engineering, The University of Sheffield, Sheffield, UK Solid-state circuit breakers (SSCBs) are designed to interrupt fault currents typically several orders faster than its electromechanical counterparts. However, such an ultrafast switch- Correspondence ing operation would produce a dangerous overvoltage which might cause damages to Zhongying Wang, Department of Electronic and SSCBs and other circuit elements in the system.
    [Show full text]
  • AC “Back to Back” Switching Device in Industrial Application
    energies Article AC “Back to Back” Switching Device in Industrial y Application Roberto Faranda 1 , Hossein Hafezi 2,* , Kishore Akkala 1 and Massimo Lazzaroni 3 1 Department of Energy, Politecnico di Milano, 20156 Milan, Italy; [email protected] (R.F.); [email protected] (K.A.) 2 School of Technology and Innovations, Electrical Engineering, University of Vaasa, 65200 Vaasa, Finland 3 Dipartimento di Fisica, Università degli Studi di Milano, 20133 Milan, Italy; [email protected] * Correspondence: hossein.hafezi@uwasa.fi This paper is an extended version of our paper published in 2018 IEEE International Conference on y Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; doi:10.1109/EEEIC.2018.8494482. Received: 13 May 2020; Accepted: 29 June 2020; Published: 9 July 2020 Abstract: In industrial applications, among several varieties of semiconductor devices available, a silicon-controlled rectifier (SCR) is often used in managing and protecting various systems with different applications. Hence, it is of the utmost importance to design a control system which can operate over a range of electrical loads without any modifications in its hardware and/or software. This paper analyzes and investigates in detail the power circuit effects on conduction delay and SCR functioning. Moreover, two different commonly used driving systems for SCR application have been introduced, discussed, and evaluated. Concerning driving systems, here, three aspects have paramount importance and are consequently taken into consideration, namely the driver system losses, the conduction delay, and in particular, some power quality indices.
    [Show full text]
  • Commonly Used Terms in SCR (Thyristor) Power Controllers
    Application Note 1005 Commonly Used Terms in SCR (Thyristor) Power Controllers INTRODUCTION Over the years AMETEK HDR has been asked many times to compile a list of commonly used terms associated with SCR (Thyristor) Power Controls. We have tried to think of the terms you hear most often. If there are any you would like to have added, just let us know. We hope this list helps. AMBIENT TEMPERATURE - the temperature in which an SCR Power Control is expected to operate, usually 0° to 50°C. ANODE - the negative power terminal of an SCR or Diode. CATHODE - the positive power terminal of an SCR or Diode. COMMAND SIGNAL - a variable input to an SCR Power Control that determines its output setting. It can be a current, voltage or potentiometer input. CSA - Canadian Standards Association’s mark for 3rd party certification of a product to Canadian Standards. cUL - Underwriters Laboratories’ mark for 3rd party certification of a product to Canadian Standards. CURRENT LIMITING - the means for limiting or setting the maximum current level applied to the load. Should be RMS for best results. CURRENT REGULATION - the means for regulating the current in an ever-changing load resistance or linearizing the input command signal to the output current. CURRENT TRANSFORMER - commonly referred to as a CT. It is used to sense the AC current. Its output is isolated and linear to the measured current, the output is normally 0-5A. di/dt - rate of rise of applied current to an SCR as it turns on. DIODE - a semiconductor that allows current to flow in only one direction.
    [Show full text]
  • Power MOSFET Selecting Mosffets and Consideration for Circuit Design Application Note
    Power MOSFET Selecting MOSFFETs and Consideration for Circuit Design Application Note Power MOSFET Selecting MOSFFETs and Consideration for Circuit Design Description This document explains selecting MOSFETs and what we have to consider for designing MOSFET circuit, such as temperature characteristics, effects of wire inductance, parasitic oscillations, avalanche ruggedness, and snubber circuit. © 2017 - 2018 1 2018-07-26 Toshiba Electronic Devices & Storage Corporation Power MOSFET Selecting MOSFFETs and Consideration for Circuit Design Application Note Table of Contents Description ............................................................................................................................................ 1 Table of Contents ................................................................................................................................. 2 1. Selecting MOSFETs .......................................................................................................................... 3 1.1. Voltage and Current Ratings .............................................................................................................. 3 1.2. Considerations for VGS......................................................................................................................... 3 1.3. Switching Speed .................................................................................................................................. 4 2. Considerations for MOSFET Circuit Design ..................................................................................
    [Show full text]