MATH 3170 Assignment #2 Solution (20 mark)
Questions marked: 3.8.10, 3.9.12, 3.10.9, 3.11.9
3.6.4
Let Xi = fraction undertaken of investment I (I = 1, 2, …, 9).
The LP formulation is: max z = 14X1 + 17X2 + 17X3 + 15X4 + 40X5 + 12X6 + 14X7 + 10X8 + 12X9 s.t. 12X1 + 54X2 + 6X3 + 6X4 + 30X5 + 6X6 + 48X7 + 36X8 + 18X9<=50 (Year 1) 3X1 + 7X2 +6X3 + 2X4 + 35X5 + 6X6 + 4X7 + 3X8 + 3X9<=20 (Year 2) All variables>=0.
Note that the question does not mention that the cash not used in Year 1 can be used in Year 2.
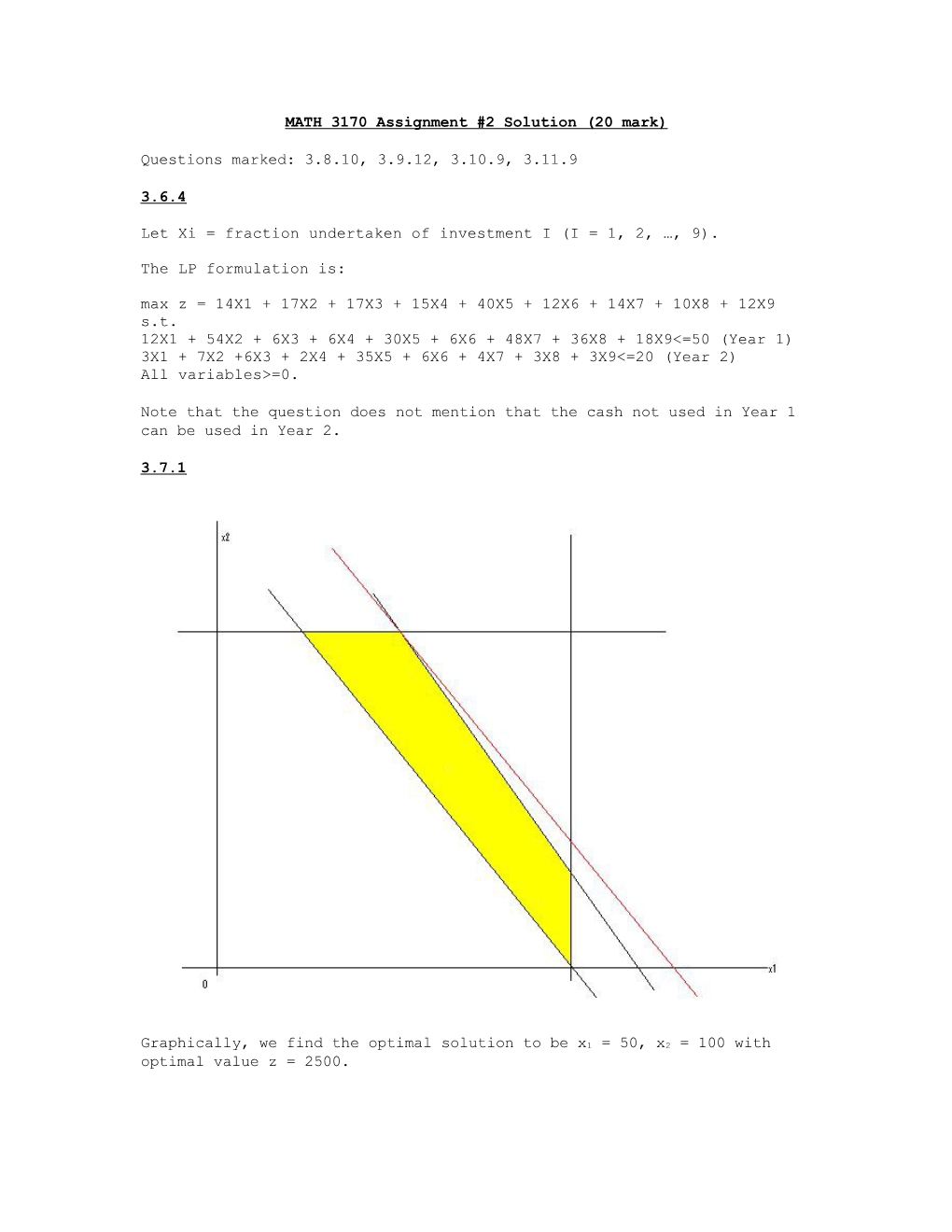
3.7.1
Graphically, we find the optimal solution to be x1 = 50, x2 = 100 with optimal value z = 2500. 3.8.10 (5 marks)
Let Mi = Tons of coal shipped from Mine i and Xij = Tons of coal shipped from Mine i to Customer j. Here is appropriate formulation in LINDO:
MIN 50 M1 + 55 M2 + 62 M3 + 4 X11 + 6 X12 + 8 X13 + 12 X14 + 9 X21 + 6 X22 + 7 X23 + 11 X24 + 8 X31 + 12 X32 + 3 X33 + 5 X34 SUBJECT TO 2) M1 <= 120 3) M2 <= 100 4) M3 <= 140 5) X11 + X21 + X31 = 80 6) X12 + X22 + X32 = 70 7) X13 + X23 + X33 = 60 8) X14 + X24 + X34 = 90 9) 0.08 M1 + 0.06 M2 + 0.04 M3 <= 15 10) 0.05 M1 + 0.04 M2 + 0.03 M3 <= 12 11) M1 - X11 - X12 - X13 - X14 = 0 12) M2 - X21 - X22 - X23 - X24 = 0 13) M3 - X31 - X32 - X33 - X34 = 0 END
Of course, all variables are nonnegative.
Constraint (9) comes from 0.08M1+0.06M2+0.04M3 <= 0.05(M1+M2+M3) but since we know M1+M2+M3 is simply the sum of all the Xij’s which is 80+70+60+90=300, the RHS is imply 0.05(300)=15. Establishing constraint (10) is similar.
You can do the above formulation without defining M1, M2 and M3 by simply replacing each Mi with the corresponding expression given in (11) to (13).
3.9.12 (5 marks)
Let A = hundreds of liters of A purchased and processed B = hundreds of liters of B produced from A and processed C = hundreds of liters of C from A D = hundreds of liters of D from processed C iS = hundreds of liters of i sold (i=B,C or D) CP = hundreds of liters of C processed iL = hundreds of liters of product i left unsold (i=B,C or D)
The correct LP formulation in LINDO is as follows:
MAX 12 BS + 16 CS + 26 DS - 9 A - CP SUBJECT TO 2) - CS - CP + C - CL = 0 3) - BS + B - BL = 0 4) - DS + D - DL = 0 5) BS <= 30 6) CS <= 60 7) DS <= 40 8) - 0.6 A - 0.4 CP + B = 0 9) - 0.4 A + C = 0 10) - 0.6 CP + D = 0 11) 3 A + CP <= 200 END
Of course, all variables are nonnegative. Note that there are many different ways to model this problem as an LP problem. The above formulation is just one of them.
3.10.9 (5 marks)
Let xi = number of workers who get quarter i off it = inventory of mixers at end of quarter t mt = mixers produced during quarter t
The LP formulation is: min z = 30(i1 + i2 + i3 + i4) + 30,000(x1 + x2 + x3 + x4) s.t. i1 = 600 + m1 - 4000, i2 = i1 + m2 - 2000 i3 = i2 + m3 - 3000, i4 = i3 + m4 - 10,000 m1500(x2 + x3 + x4), m2500(x1 + x3 + x4), m3500(x1 + x2 + x4), m4500(x1 + x2 + x3) All variables 0
3.11.9 (5 marks)
Let Pi = Fraction of project I invested in, Bt = Money borrowed at time t, Ct= ending cash position at time t max z = 5.5P1 +6P3-P2+1.03C2.5-1.035B2.5 s.t.
C0 = 2-3P1-2P2-2P3+B0 C.5=1.03C0-1.035B0-P1-.5P2-2P3+B.5 C1=1.03C.5-1.035B.5+1.8P1+1.5P2-1.8P3+B1 C1.5=1.03C1-1.035B1+1.4P1+1.5P2+P3+B1.5 C2=1.03C1.5-1.035B1.5+1.8P1+1.5P2+P3+B2 C2.5=1.03C2-1.035B2+1.8P1+.2P2+P3+B2.5 All Bt<=2 ALL VARIABLES >=0
The above formulation assumes that all debts with interest must be repaid in exactly 6 months.