Kinematics of Mobile Robot Platforms:
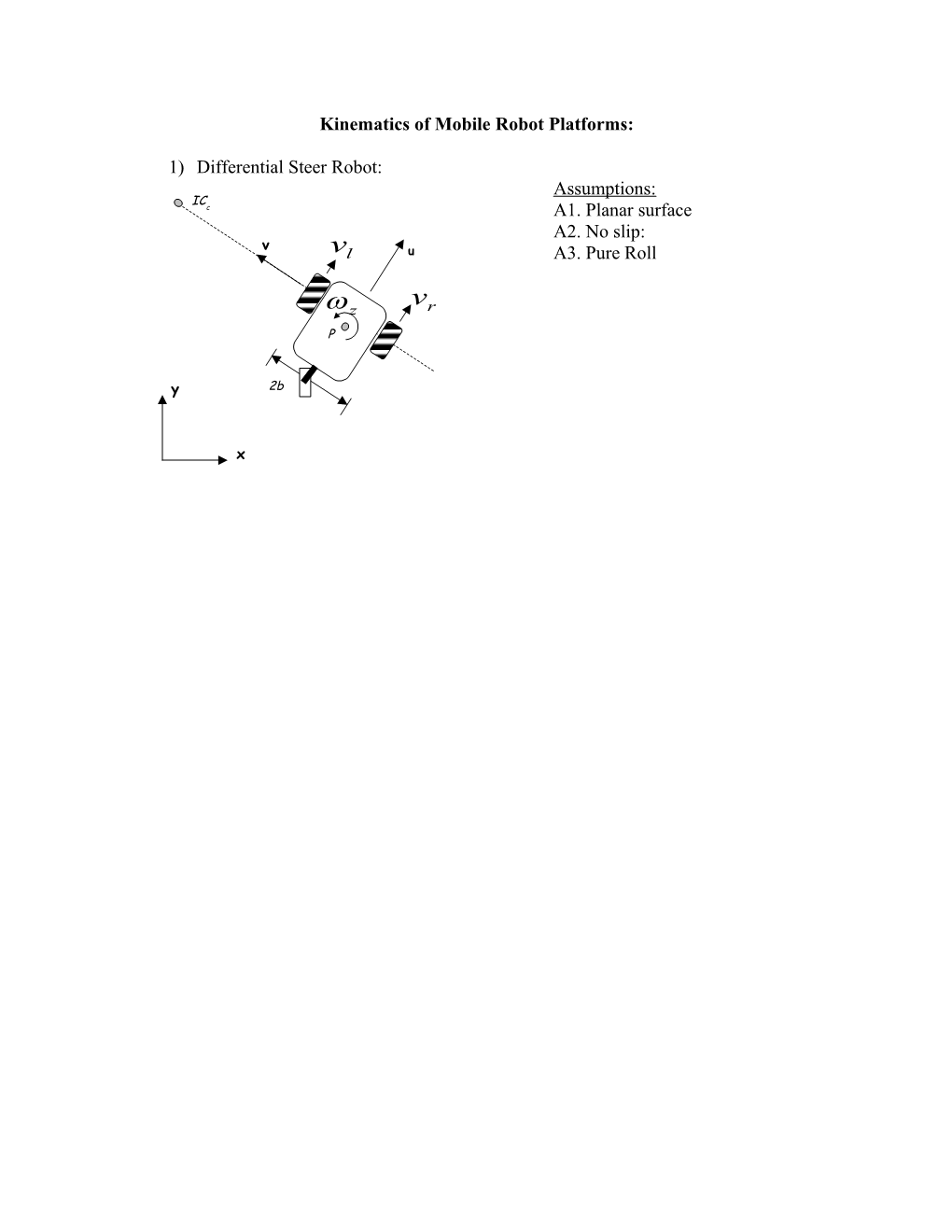
1) Differential Steer Robot: Assumptions: IC c A1. Planar surface A2. No slip: v vl u A3. Pure Roll v z r P y 2b
x 2) Tricycle Steer Robot: Assumptions A1. Planar Surface A2. No Slip A3. Pure Roll u
ICc v z P
y 2b
x 3. Skid-steer Robot: Assumptions:
ICc A1. Planar Surface
IC ˙ l l rll u
v V c ˙ r rr r z P
ICr
y 2b
x
Consider a model as shown in the figure below, consisting of 3 bodies, the chassis as the center body and the contact patch of each track as separate bodies connected to the chassis with prismatic joints. CP l x y RC b m CP C r
Y 2b b m l
X The prismatic joint motion is related to the wheel rotation through the following kinematics:
˙ ˙ (1) dl rl r and ˙ ˙ (2) dr l r r Now consider the model with instant centers identified for each of the three bodies: IC
IC l x y r Icl-A r A ICl r r C-A ICr C r C-B IC r r B Icl-B Y
X
The velocity of an arbitrary point on CPl, A is given as, ˙ (3) v A vC z rCA dl xˆ where rC-A is a vector from point C to A as shown in Fig. 3. Similarly, the velocity of an arbitrary point on CPr , B is given as, ˙ (4) v B vC z rCB d r xˆ where rC-B is a vector from point C to B as shown in Fig. 3. The velocity of points A and B can be described in terms of rotation about the instant centers associated with CPl, CPr respectively as, v r (5) A z ICl A v r (6) B z ICr B where rICl-A is a vector from the instant center of CPl to A and rICl-B, is a vector from the instant center of CPr to B as shown on the figure above. Combining equations 1, 3 and 5 for the left track, 2, 4, and 6 for the right track, and collecting terms through the distributive nature of addition in the cross product yields
0 v r r d˙ xˆ C z CA ICl A l (7) 0 v r r d˙ xˆ C z CB ICl B r (8) or ˙ r xˆ v r l l l C z ICl (9) ˙ r xˆ v r r r r C z ICr (10) T T Where rICl = (xic, ylic) , rICr = (xic, yric) , are vectors from the robot chassis centroid (C) to the instant T centers for CPl and CPr respectively and vC = (vx, vy) is the velocity of the robot at C. These equations are expanded into scalar components,
˙ vx z ylic r l l l (11) v y z xic 0 ˙ vx z yric r r r r (12) vy z xic 0 and then combined into the matrix expression,
vx ˙ J v J l 1 y 2 ˙ (13) r z where
1 0 ylic J 1 0 y 1 ric (14) 0 1 xic
l rl 0 J 0 r 2 r r (15) . 0 0 The direct kinematics of the tracked robot system is written in its usual form as,
vx ˙ v K l y eq ˙ (16) r z where
yricl rl ylic r rr 1 K J 1J x r x r eq 1 2 ic l l ic r r . (17) yric ylic l rl r rr 4: Vehicle with Trailer castors:
ICc u a 2 2 2 - 1
v 90- 2
co2
c a1
a + 90 3 1
y 1
co 1 x 1
Encoders report the orientation (1, 2) and rotation (1, 2) of each wheel. Based on these measurements, estimates (termed actual for the purposes of this paper) of the robot motion are given as:
T * * * * ˙ (1) Vu ,Vv , z f 1 , 2 , 1
With
* ˙ f1 1 , 2 , 1 Vu ˙ r sin a cos cos 1 1 2 1 3 2 1 co1 sin 1 a3 cos 2 sin 2 1 (2) * ˙ f 2 1 , 2 , 1 Vv ˙ r sin a cos sin 1 1 2 1 3 2 1 c1 co1 cos1 a3 cos 2 sin 2 1 (3) ˙ * ˙ 1r1 sin 2 1 f3 1 , 2 , 1 (4) a3 cos 2
Where
2 2 a3 c1u c2u c1v c2v
2 2 c1 co1 cos 1 c2 co2 cos 2 co1 sin 1 co2 sin 2 (5) and
atan 2c2v c1v ,c2u c1u
atan 2 co2 sin 2 co1 sin 1 ,c2 co2 cos 2 c1 co1 cos 1 (6)
The geometric parameters, c1, c2, co1, co2 are shown in Fig. 4 and c1u, c1v, c2u, c2v are the (u,v) coordinates along c1, c2.