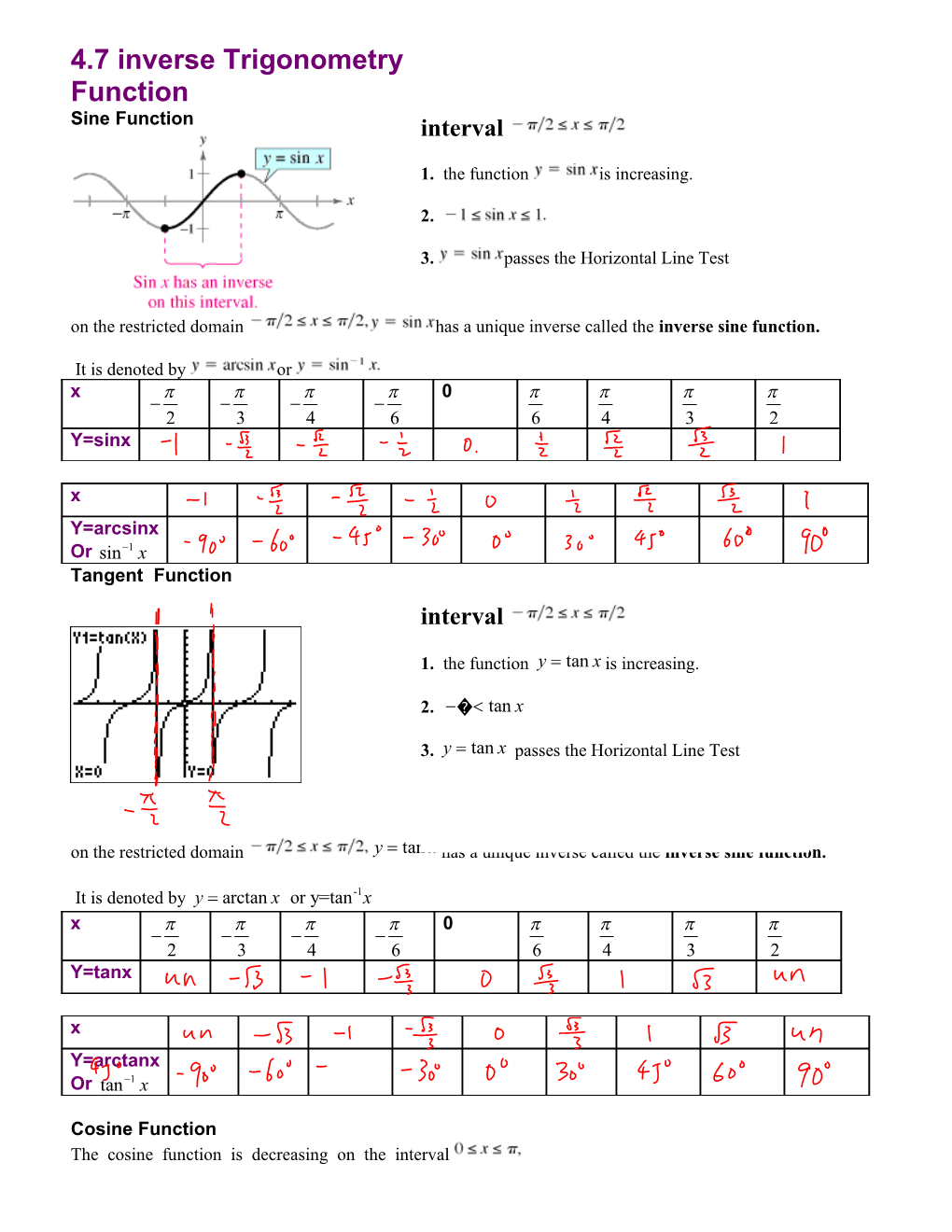
4.7 inverse Trigonometry Function Sine Function interval
1. the function is increasing.
2.
3. passes the Horizontal Line Test on the restricted domain has a unique inverse called the inverse sine function.
It is denoted by or x p p p p 0 p p p p - - - - 2 3 4 6 6 4 3 2 Y=sinx x Y=arcsinx Or sin-1 x Tangent Function interval
1. the function y= tan x is increasing.
2. -� < tan x
3. y= tan x passes the Horizontal Line Test
on the restricted domain y= tan x has a unique inverse called the inverse sine function.
It is denoted by y= arctan x or y=tan-1 x x p p p p 0 p p p p - - - - 2 3 4 6 6 4 3 2 Y=tanx x Y=arctanx Or tan-1 x
Cosine Function The cosine function is decreasing on the interval interval
1. the function y= cos x is decreasing.
2. -1# cosx 1
3. y= cos x passes the Horizontal Line Test
on the restricted domain has a unique inverse called the inverse cosine function.
It is denoted by y= arccos x or y=cos-1 x x 0 p p p p 2p 3p 5p p 6 4 3 2 3 4 6 Y=cosx x Y=arccosx Or cos-1 x Cotangent Function interval
1. the function y= cot x is decreasing.
2. -� < cot x
3. y= cos x passes the Horizontal Line Test on the restricted domain has a unique inverse called the inverse cosine function.
It is denoted by y= arccot x or y=cot-1 x x 0 p p p p 2p 3p 5p p 6 4 3 2 3 4 6 Y=cotx x Y=arccotx Or cot-1 x
Example 1 If possible, find the exact value.
c.
d.
e.
f.
g.
h.
i.
Example 2
Sketch a graph of y=arccotx Example 3 Use a calculator to approximate the value (if possible). a. b. c.
Properties If and then and
If and then and
If x is a real number and then and
Keep in mind that these inverse properties do not apply for arbitrary values of x and y. For instance,
In other words, the property is not valid for values of y outside the interval
EXAMPLE 4 Using Inverse Properties If possible, find the exact value.
=
d.
e.
f.
EXAMPLE 5 Find the exact value of
(a) and (b)
EXAMPLE 6 Write each of the following as an algebraic expression in x. a.
b.
c.
Summary: