High Performance Computing for Engineering Applications

ME964 High Performance Computing for Engineering Applications Midterm Project

For the midterm project, you will have to solve a collision detection problem: given an R ＃R R arbitrary number N of rigid spheres of radii Ri , i = 1, ,N with low i high distributed in the 3D space, find out which spheres are in contact/penetration with which other spheres. Once you find a pair of spheres that are in contact, for this contact instance compute: - absolute collision location on object A (a vector in 3 ) - absolute collision location on object B (a vector in 3 ) - collision normal unit vector from body B to A (a vector in 3 ) - object id for body A - object id for body B

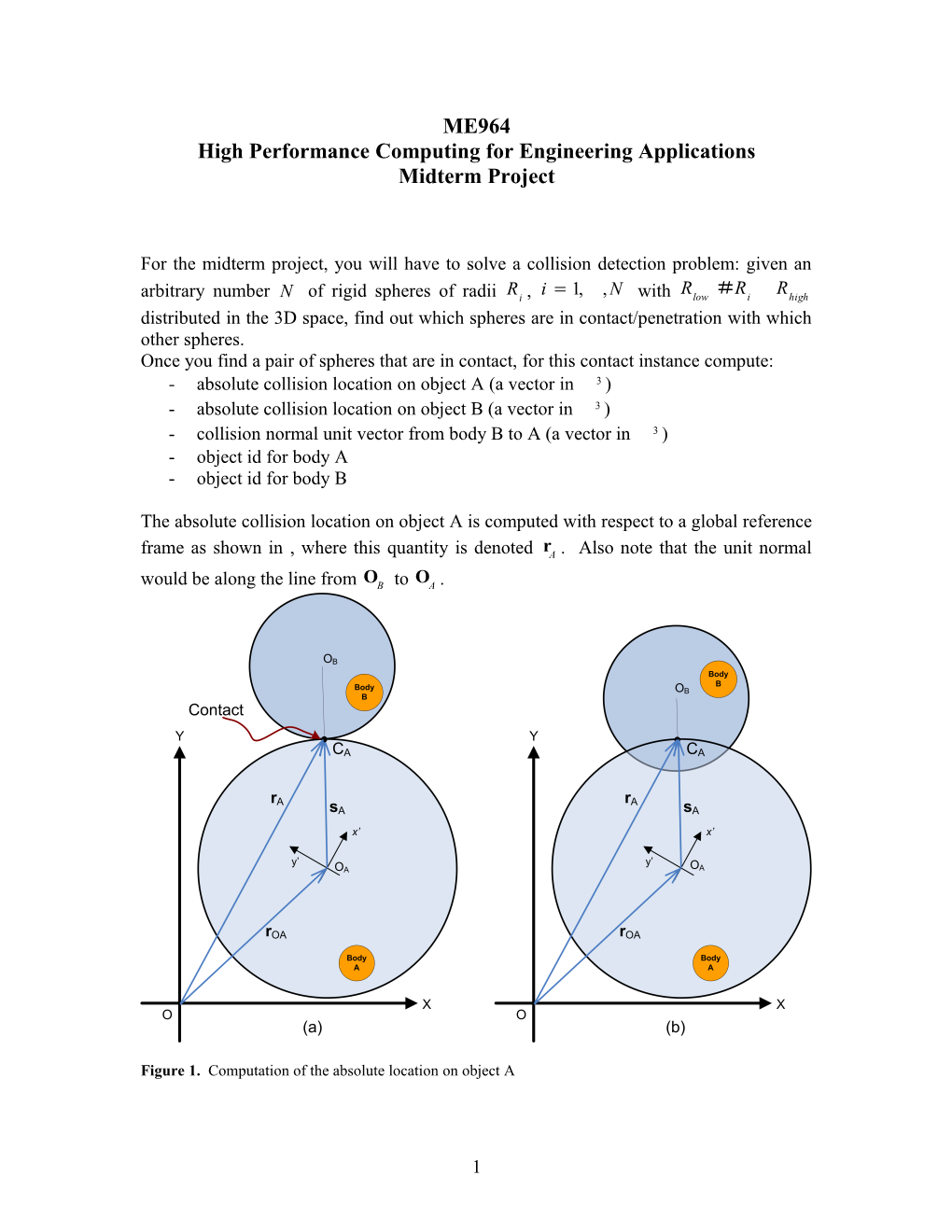
The absolute collision location on object A is computed with respect to a global reference frame as shown in , where this quantity is denoted rA . Also note that the unit normal would be along the line from OB to OA .

Figure 1. Computation of the absolute location on object A

1 In order to understand what Bullet does and to increase your chances of matching its behavior, below is listed a summary of possible collision cases: A: B:

A B A B A

(a) (b) (c) (d)

Figure 2. Possible contact scenarios

1. Sphere contacts sphere: one contact point (C A C B ), normal from center of B to center of A. This scenario is captured in (a).

2. Sphere interpenetrates sphere: two different points C A and C B . This scenario is captured in (b) as well as in Figure 2(a). 3. Sphere exactly on top of sphere, see Figure 2(b). 4. Sphere inside sphere see Figure 2(c). 5. Sphere inside sphere, not concentric, see Figure 2(d). 6. Spheres are not in contact, not shown

For this project: 1) Run the collision detection engine provided with the physics engine “Bullet” to verify the accuracy of your results. Using the Microsoft Developer Studio Solution provided, this process is automated to the extent to which you will get a message “Test Passed” or “Test Failed”. In order to pass the test, the following conditions must be satisfied: i) you should find the same number of contacts as “Bullet” does ii) you should find the same values for the absolute collision location on object A and B (see ) iii) you should find a contact normal that is within 10 from the Bullet normal NOTE: When you have a pair of bodies A and B, make sure you have the body A be of lower index. Specifically, when running the comparison with Bullet, please make sure that output is sorted by body A and then body B in increasing order.

2 2) Run a work analysis for your algorithm and Bullet, and compare their performance. Specifically, run a collision detection for 1024, 4096,…,1048576 bodies and do a regression analysis to gauge how your algorithm scales with the number of bodies. 3) Read Chapter 5 of the textbook Patterns for Parallel Programming by Timothy G. Mattson, Beverly A. Sanders, Berna L. Massingill. Drawing on material you read out of this book (chapters 3, 4, and 5), comment on the patterns that you used in designing the collision detection solution.

Grading:

. Solving the collision detection problem on the GPU but not passing the Bullet validation: 30% . Passing the Bullet validation: 10% . Running the regression analysis and understanding the scaling of both Bullet and your implementation: 20% . Report on the parallel programming patterns that you used in your design: 15% . PPT report and your presentation of the design and results (presentation will be made on Nov. 18): 25% . Running collision detection faster than Bullet: Priceless

Submission Policy: Submit your Developer Studio Solution along with the MS-Word doc report no later than November 9, 11:59 PM if you choose to implement a brute force approach, or by November 17, 11:59 PM if you implement a more sophisticated approach.

NOTE: The PPT report is due on November 17, 11:59 PM. Your presentation is slated for Nov. 18 during regular class hours. You will have a 10 minute time slot to make your presentation. The material and your presentation will account for 25%.