Entropy Concentration

Opdracht 10.

Koninkrijk.

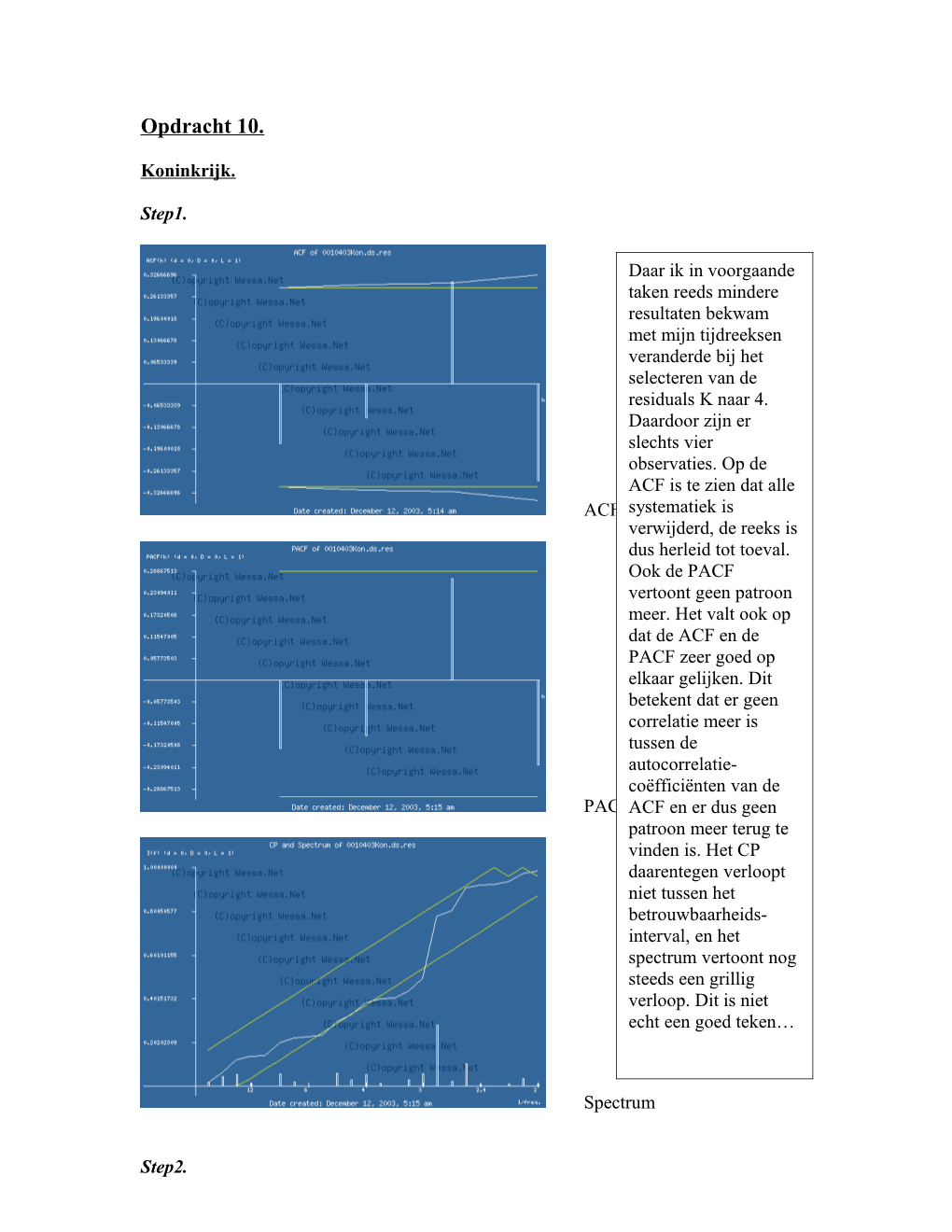
Step1.

Daar ik in voorgaande taken reeds mindere resultaten bekwam met mijn tijdreeksen veranderde bij het selecteren van de residuals K naar 4. Daardoor zijn er slechts vier observaties. Op de ACF is te zien dat alle ACF systematiek is verwijderd, de reeks is dus herleid tot toeval. Ook de PACF vertoont geen patroon meer. Het valt ook op dat de ACF en de PACF zeer goed op elkaar gelijken. Dit betekent dat er geen correlatie meer is tussen de autocorrelatie- coëfficiënten van de PACFACF en er dus geen patroon meer terug te vinden is. Het CP daarentegen verloopt niet tussen het betrouwbaarheidsinterval, en het spectrum vertoont nog steeds een grillig verloop. Dit is niet echt een goed teken…

Spectrum

Step2. Voor het histogram heb ik K op de maximum- waarde 32 gezet. We zien duidelijk dat er geen normaalverdeling inzit. Het rootogram toont het verschil tussen de werkelijke Histogram frequenties en de theoretische frequenties van het histogram van een normaalverdeling. Het rootogram voor K = 4 ziet er anders vrij goed uit, maar dit is relatief daar K = 4. De residu’s van deze tijdreeks zijn absoluut niet normaal verdeeld. RootogramOp de grafiek van de entropy concentration is eveneens niet echt een normaalverdeling te bemerken.

Entropy Concentration

Step3.

Skewness and Kurtosis - Ungrouped Data Skewness Measure Value Kurtosis Measure Value FISHER 3rd Cent. Mom. 126332016.51128 FISHER 4th Cent. Mom. 1925720553485.4 FISHER beta 1 0.029258078563798 FISHER beta 2 2.884513410145 FISHER gamma 1 0.17104993003155 FISHER gamma 2 -0.11548658985502 FISHER gamma 1 (S.E.) 0.35355339059327 FISHER gamma 2 (S.E.) 0.70710678118655 FISHER Test 1 0.48380226178718 FISHER Test 2 -0.16332270164518 FISHER Test 1 Probability 0.6242 FISHER Test 2 Probability 0.865

Trimmed Skewness and Kurtosis (small sample) - Ungrouped Data Probabilit Skewness Measure (small sample) Value Kurtosis Measure (small sample) Value Probability y

Trimmed Skewness (0/48) 0.1766 0.603 Trimmed Kurtosis (0/48) 0.0077 0.984

Trimmed Skewness (1/48) -0.0379 0.9124 Trimmed Kurtosis (1/48) -0.4595 0.5028

Trimmed skewness

Trimmed kurtosis

In de tabel is af te lezen dat de skewness 62% en de kurtosis 86% afwijkt van de perfecte normaalverdeling. De skewness zou nul moeten zijn, wat niet is (zie Step3.grafiek). De kurtosis’eerste waarde is wel ongeveer nul, en de grafiek daalt ook. De kurtosis meet de dikte van de staart van de normaalverdeling. De nul-lijn ligt bij beide grafieken wel binnen het betrouwbaarheidsinterval. Het gemiddelde van de residuwaarden van de tijdreeks ligt steeds tussen het betrouwbaarheidsinterval en schommelen rond de nul. De residuwaarden zijn dus niet significant verschillend van 0. Het valt verder op dat de Trimmed Mean een gladder verloop kent dan de Windsor Mean.

Central Tendency

Step4.

Variability - Ungrouped Data Variability Measure Value Interquartile Difference (Weighted Average at 1237.4295137609 Xnp) Observations 48

Percentiles - Ungrouped Data Empirical Empirical True Basic Weighted Weighted Empirical MS Excel Distribution Distribution Closest - Statistics % Average at Average at Distribution (old Function - Function - Observation Graphics Xnp X(n+1)p Function versions) Averaging Interpolation Toolkit 0.01 -858.4659 -876.3506 -1788.4705 -1788.4705 -1743.8986 0 -912.12 0 - 0.05 -1659.9711 -1618.8242 -1618.8242 -1574.2037 -1693.6367 -1652.4898 -1693.6367 1663.7117 0.15 -888.1083 -867.0384 -775.7355 -775.7355 -774.7973 -916.2015 -824.8986 -916.2015 0.25 -667.9341 -667.5005 -667.9341 -667.067 -666.6335 -667.9341 -666.6335 -667.9341 0.4 -354.6001 -352.8875 -351.175 -351.175 -352.0313 -355.4563 -353.7438 -351.175 0.5 84.2742 86.9764 84.2742 86.9764 86.9764 84.2742 86.9764 86.9764 0.6 280.0407 295.9459 287.7556 287.7556 291.8508 287.7556 300.041 287.7556 0.75 569.4954 616.0899 569.4954 600.5584 585.0269 569.4954 585.0269 631.6214 0.99 2136.4504 1173.3693 2394.6313 2394.6313 2141.8292 2394.6313 1221.262 0

Quartiles - Ungrouped Data Method Quartile 1 Quartile 2 Quartile 3 Weighted Average at Xnp -667.93407914533 84.274155230041 569.49543461561

Wanneer we naar de percentielen kijken zouden de waarden tegenover elkaar (bijvoorbeeld 0,75 en 0,25) in absolute waarde ongeveer dezelfde moeten zijn. Ik kan enkel vaststellen dat dit allesbehalve het geval is. Wanneer we bij de kwartielen het verschil nemen tussen het eerste en derde kwartiel, zouden we het interquartiele difference moeten bekomen. Dit klopt natuurlijk, maar het verschil is een vrij grote waarde. Om plaats/geheugen te besparen heb ik me beperkt tot enkele gegevens…

Step5.

Volgens mij zijn de residu’s van deze tijdreeks geen white noise. De resultaten zijn bij momenten iets te slecht…

Step6.

Deze stap volgt na de laatste analyse van mijneigen tijdreeksen, dus op het eind van de analyse van het Waals Gewest. Vlaams Gewest

Step1.

Deze tijdreeks gaf bij voorgaande opdrachten de slechtste resultaten van allemaal. De ACF en PACF vertonen geen patroon, en gelijken redelijk op elkaar. Het CP verloopt nog steeds zeer grillig en de spectrum vertoont vrij hoge pieken. PACF

Spectrum Step2.

Histogram

Rootogram

Concentration

Het histogram en rootogram geven niet weer dat er sprake zou zijn van een normaalverdeling, wat eveneens te zien is op de laatste grafiek. Step3.

Skewness and Kurtosis - Ungrouped Data Skewness Measure Value Kurtosis Measure Value FISHER 3rd Cent. Mom. -147316271.51489 FISHER 4th Cent. Mom. 2623701406628.3 FISHER beta 1 0.053120426009497 FISHER beta 2 4.7652733292092 FISHER gamma 1 -0.2304786888402 FISHER gamma 2 1.7652733292092 FISHER gamma 1 (S.E.) 0.35355339059327 FISHER gamma 2 (S.E.) 0.70710678118655 FISHER Test 1 -0.65189217519156 FISHER Test 2 2.4964734834632 FISHER Test 1 Probability 0.5092 FISHER Test 2 Probability 0.0124

Trimmed Skewness (0/48) -0.238 0.484 Trimmed Kurtosis (0/48) 2.1002 0.0018

Trimmed Skewness (1/48) 0.0826 0.8104 Trimmed Kurtosis (1/48) -0.136 0.8414

Trimmed Skewness (2/48) 0.0318 0.9282 Trimmed Kurtosis (2/48) -0.1246 0.8572

Trimmed skewness Trimmed kurtosis

De skewness en kurtosis verlopen bijzonder grillig. Ook is enkel de kurtosis Step4.significant verschillende van nul, doch kent ze geen constant dalend verloop zoals te zien is op de grafiek. Variability - Ungrouped Data Variability Measure Value Interquartile Difference (Weighted Average at 864.3 Xnp)

Percentiles - Ungrouped Data Empirical Empirical True Basic Weighted Weighted Empirical MS Excel Distribution Distribution Closest - Statistics % Average at Average at Distribution (old Function - Function - Observation Graphics Xnp X(n+1)p Function versions) Averaging Interpolation Toolkit 0.01 -1358.931 -1387.2421 -2831.1062 -2831.1062 -2140.9113 0 -1443.8642 0 - 0.05 -1310.6312 -1247.1063 -1247.1063 -1236.8863 -1362.6063 -1299.0813 -1362.6063 1316.4063 0.15 -890.2663 -881.9113 -845.7062 -845.7062 -845.3712 -901.4063 -865.2012 -901.4063 0.25 -406.8062 -388.8312 -406.8062 -370.8562 -352.8813 -406.8062 -352.8813 -406.8062 0.4 -185.6262 -163.4662 -141.3063 -141.3063 -152.3862 -196.7063 -174.5463 -141.3063 0.5 48.1938 50.0437 48.1938 50.0437 50.0437 48.1938 50.0437 50.0437 0.75 457.4937 458.3938 457.4937 458.0938 457.7937 457.4937 457.7937 458.6938 0.99 1990.5017 1175.3599 2398.6937 2398.6937 1999.0058 2398.6937 1223.3338 0

Quartiles - Ungrouped Data Method Quartile 1 Quartile 2 Quartile 3 Weighted Average at Xnp -406.80625 48.19375 457.49375

De analyse van deze cijfers is analoog naar de analyse gemaakt bij de tijdreeks Koninkrijk… Step5.

Wederom kom ik tot de conclusie dat de residu’s geen white noise zijn…

Step6. Zie later

Antwerpen.

Step1.

De ACF vertoont geen patroon meer, maar gelijkit ook niet echt op de waarden van de PACF. Het CP loopt buiten het BI en het spectrum geeft nog steeds grillige sprongen weer. Allemaal slechte tekens in ons ACF onderzoek of de residuals wel white noise zijn of niet.

PACF Spectrum

Step2.

Histogram

Rootogram Concentration

Enkele van bovenstaande grafieken vertelt ons dat er een normaal verdeling heerst. Zo geeft de output van het rootogram weer dat de reeks normaal verdeeld is, geen enkel staafje ligt buiten het BI. Op de onderste grafiek is eveneens een lichte normaalverdeling waar te nemen.

Step3.

Skewness and Kurtosis - Ungrouped Data Skewness Measure Value Kurtosis Measure Value FISHER 3rd Cent. Mom. -39421664.174204 FISHER 4th Cent. Mom. 207755189151.26 FISHER beta 1 0.1117456589572 FISHER beta 2 3.5924636465915 FISHER gamma 1 -0.33428380002208 FISHER gamma 2 0.59246364659148 FISHER gamma 1 (S.E.) 0.35355339059327 FISHER gamma 2 (S.E.) 0.70710678118655 FISHER Test 1 -0.94549736734569 FISHER Test 2 0.83787012422269 FISHER Test 1 Probability 0.3422 FISHER Test 2 Probability 0.4008

Trimmed Skewness (0/48) -0.3452 0.3124 Trimmed Kurtosis (0/48) 0.7954 0.238

Wegens een probleem met de software was het niet mogelijk de grafieken te kopiëren. Daarom volgt een schriftelijke beschrijving. Van de twee grafieken liggen de nul-lijnen binnen het BI. Bij beide grafieken is de eerste waarde niet nul, en zo kent de grafiek van de kurtosis geen dalend verloop zoals zou moeten.

Step4. We merken op dat het gemiddelde niet rond de nul-lijn hangt. Beide liggen boven deze nul-lijn. De trimmed mean is zoals gewoonlijk gladder dan de Winsorized mean. Bij gebrek aan geheugen heb ik de output van percentielen, kwartielen en variantie niet weergegeven, maar de uitleg is analoog naar voorgaande modellen…

Central Tendency Step5.

Door te veel negatieve resultaten kan ik niet oordelen dat de residu’s white noise zijn.

Step6.

Later… Waals Gewest.

Step1.

Het ACF en PACF vertonen geen patronen meer, en de eerste waarden gelijken erg op elkaar. Het CP verloopt niet volledig tussen het BI, maar is toch beter dan bij vorige modellen. Het spectrum geeft nog wel enkele hoge staafjes weer.

ACF PACF

Spectrum

Step2.

Histogram Rootogram

Concentration

De output van het rootogram geeft weer dat deze reeks normaal verdeeld is. Enkel het eerste staafje gaat buiten het BI. Op het histogram is deze normaalverdeling echter niet meteen duidelijk. Ook op de onderste grafiek kunnen we moeilijk een normaalverdeling onderscheiden.

Step3.

Skewness and Kurtosis - Ungrouped Data Skewness Measure Value Kurtosis Measure Value FISHER 3rd Cent. Mom. 248950.11087944 FISHER 4th Cent. Mom. 1162108864.7297 FISHER beta 1 0.0073157600665205 FISHER beta 2 2.7964261267623 FISHER gamma 1 0.085532216541608 FISHER gamma 2 -0.20357387323769 FISHER gamma 1 (S.E.) 0.35355339059327 FISHER gamma 2 (S.E.) 0.70710678118655 FISHER Test 1 0.24192164130595 FISHER Test 2 -0.28789693247756 FISHER Test 1 Probability 0.8026 FISHER Test 2 Probability 0.7718

Wederom ben ik er niet in geslaagd de grafieken te kopiëren, hij bleef enkel de kader kopiëren. Op beide grafieken ligt de nul-lijn binnen het BI. De eerste waarde van de skewness-grafiek is echter niet nul, die van de kurtosis grafiek wel. Deze kent ook een dalend verloop. Step4.

De uitleg voor de percentielen, kwartielen en varianties zijn analoog naar voorgaande modellen.

Step5.

De residu’s vormen geen white noise.

Step6.

Wegens problemen met Excel was het voor mij onmogelijk scatterplots te maken. Excel crashte wanneer ik een grafiek wou aanmaken, bijzonder frustrerend. Ik begrijp dat er natuurlijk geen punten voor dit deel van deze taak gegeven worden. Ik voorspel wel dat er geen enkel verband is tussen de residu’s van de reeksen, dit was eveneens niet het geval bij een voorgaande taak.

Het cumulatieve periodogram ligt binnen het Unemployment. betrouwbaarheidsinterval en het spectrum vertoont geen Step1. golfbewegingen meer. Op de ACF is te zien dat alle patronen zijn verwijderd, de reeks is dus herleid tot puur toeval. Ook de PACF vertoont geen proces meer. Het valt ook op dat de ACF en de PACF goed op elkaar lijken. Dit betekent dat er geen correlatie meer is tussen de autocorrelatiecoëfficiënten van de ACF en er dus geen trend meer terug te vinden is. Er zijn dus geen verdere processen aanwezig dan de reeds gevonden waarden van p, P, q en Q. ACF

Het histogram vertoont duidelijk een vrij goede normaalverdeling. Het rootogram toont het verschil tussen de werkelijke frequenties en de theoretische frequenties van het histogram van een normaalverdeling. Buiten de Spectrumwaarden bij time lag 27 en 36 liggen alle waarden eveneens binnen het betrouwbaarheidsinterval. De output van het rootogram gaf aan dat deze Step2. tijdreeks normaal verdeeld is. Op de grafiek van de Histogram entropy concentration is eveneens een verloop van een normaalverdeling op te merken. Rootogram

Entropy concentration

Skewness/kurtosis

Skewness and Kurtosis - Ungrouped Data Skewness Measure Value Kurtosis Measure Value FISHER 3rd Cent. Mom. 0.041742168639339 FISHER 4th Cent. Mom. 0.27093430277029 FISHER beta 1 0.08034973774986 FISHER beta 2 3.4840706966149 FISHER gamma 1 0.28346029307446 FISHER gamma 2 0.48407069661493 FISHER gamma 1 (S.E.) 0.12927912407657 FISHER gamma 2 (S.E.) 0.25855824815314 FISHER Test 1 2.1926223208828 FISHER Test 2 1.872192049848 FISHER Test 1 Probability 0.0278 FISHER Test 2 Probability 0.0602

Trimmed Skewness and Kurtosis (small sample) - Ungrouped Data Probabilit Skewness Measure (small sample) Value Kurtosis Measure (small sample) Value Probability y Trimmed Skewness (0/359) 0.2847 0.0264 Trimmed Kurtosis (0/359) 0.5078 0.0478 Trimmed Skewness (1/359) 0.2744 0.0332 Trimmed Kurtosis (1/359) 0.2562 0.3174 Trimmed Skewness (2/359) 0.2391 0.0644 Trimmed Kurtosis (2/359) 0.0154 0.9522

In de tabellen kunnen we aflezen dat de skewness slechts 2,78% en de kurtosis slechts 6,02% afwijkt van de perfecte normaalverdeling. De nul- lijn van de grafieken zou binnen het BI moeten liggen, maar dit is voor de reschterkant van de kurtosis grafiek niet het geval. Daarom is enkel de linkerzijde significant. De skewness blijkt alles behalve nul te zijn, wat niet echt een goed teken is. De kurtosis meet de dikte van de staart van de normaalverdeling.

Step3. Het gemiddelde van de residu’s ligt dicht bij de waarde nul, dit is positief. Verder merken we op dat de trimmed mean een gladder verloop kent dan de winsorized mean.

Step 4.

Variability

Variability - Ungrouped Data Variability Measure Value Interquartile Difference (Weighted Average at Xnp) 0.65286916002406

Quartiles

Quartiles - Ungrouped Data Method Quartile 1 Quartile 2 Quartile 3 Weighted Average at Xnp -0.33852680243119 -0.026767207103008 0.31434235759287 Percentiles

Percentiles - Ungrouped Data Empirical Empirical True Basic - Weighted Weighted Empirical MS Excel Distribution Distribution Closest Statistics % Average at Average at Distribution (old Function - Function - Observation Graphics Xnp X(n+1)p Function versions) Averaging Interpolation Toolkit 0.05 -0.8718 -0.8717 -0.8717 -0.8717 -0.8704 -0.8717 -0.8717 -0.8717 0.15 -0.5072 -0.5071 -0.5071 -0.5071 -0.5005 -0.5071 -0.5071 -0.5071 0.25 -0.3385 -0.3371 -0.3371 -0.3371 -0.3354 -0.3371 -0.3371 -0.3371 0.75 0.3143 0.3159 0.3159 0.3159 0.3148 0.3138 0.3159 0.3159 0.85 0.5357 0.5382 0.5382 0.5382 0.5361 0.5352 0.5382 0.5382 0.95 0.8915 0.9016 0.9016 0.9016 0.892 0.891 0.9016 0.9016 0.96 0.959 0.9661 0.962 0.962 0.9594 0.962 0.9647 0.9688 0.97 1.0537 1.1395 1.1373 1.1373 1.0569 1.0287 1.1458 1.1373 0.98 1.2206 1.2415 1.2293 1.2293 1.2216 1.2293 1.2323 1.2445 0.99 1.3459 1.4835 1.4094 1.4094 1.347 1.3018 1.5205 1.4094

Wanneer we de resultaten van de percentielen gaan spiegelen merken we op dat de waarden elkaar in absolute waarde benaderen, wat de bedoeling zou moeten zijn. Kijk bijvoorbeeld naar 5% (-0,8718) en 95% (0,8915). Wanneer we de waarde van het eerste kwartiel aftrekken van deze van het derde kwartiel komen we dicht bij de waarde nul uit.

Step5.

De residu’s zijn white noise.

Step6.

N.v.t.