Calculating Solar Temperature
Welcome to the use of CubeSats. The easy to build, launch and use mini-satellites. Today you will be using the data downloaded from CubeSat, through the successful SwissCube site, to calculate the temperature of the Sun (The big round thing that warms the Earth up).
This activity can be used over the period of a week, by recording multiple temperature readings every day to try and determine the way the SwissCube orientates itself. Or in a single session by just recording one set of data.
Go to http://swisscube-live.ch/Home/Position and follow these instructions:
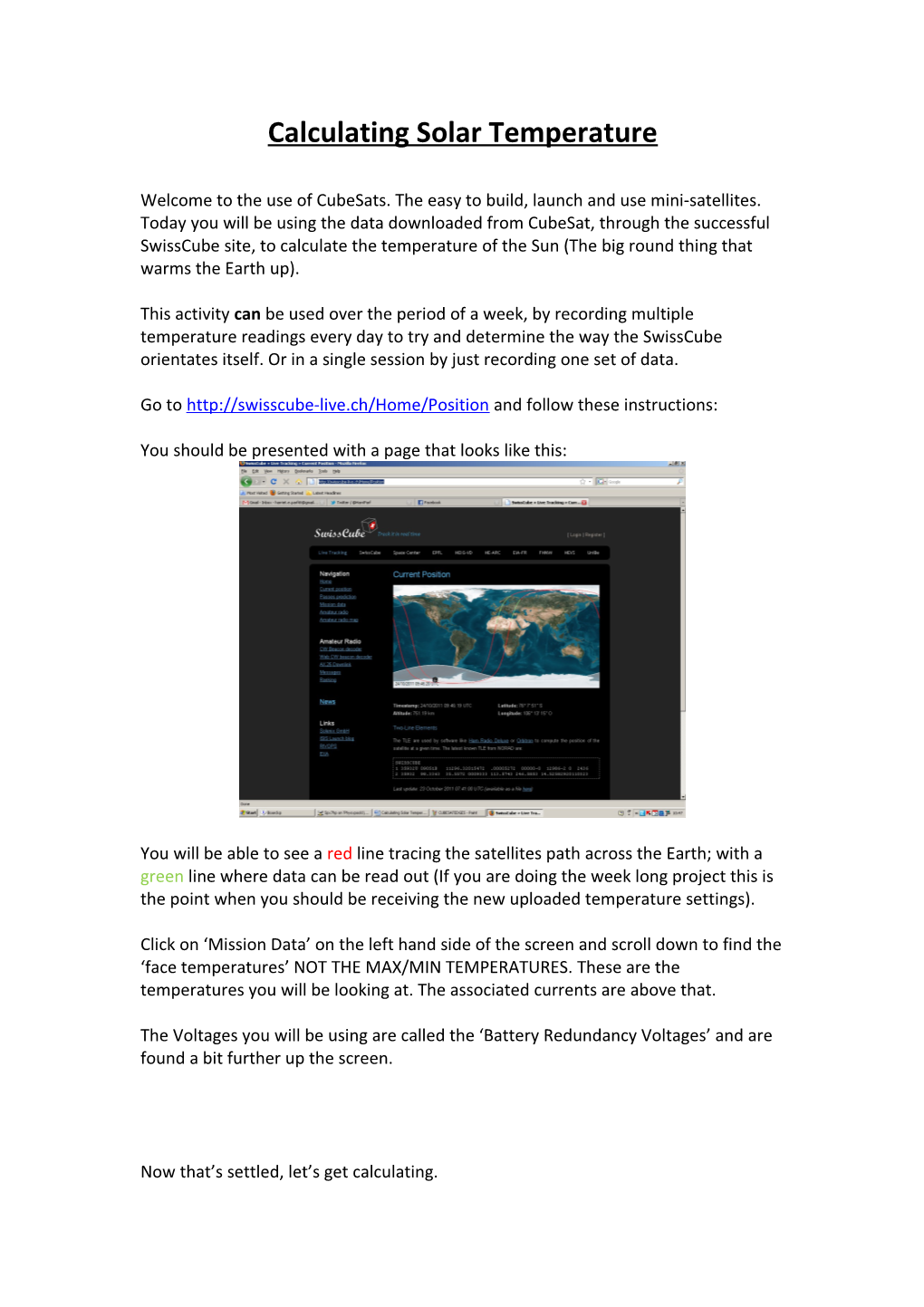
You should be presented with a page that looks like this:
You will be able to see a red line tracing the satellites path across the Earth; with a green line where data can be read out (If you are doing the week long project this is the point when you should be receiving the new uploaded temperature settings).
Click on ‘Mission Data’ on the left hand side of the screen and scroll down to find the ‘face temperatures’ NOT THE MAX/MIN TEMPERATURES. These are the temperatures you will be looking at. The associated currents are above that.
The Voltages you will be using are called the ‘Battery Redundancy Voltages’ and are found a bit further up the screen.
Now that’s settled, let’s get calculating. What is the SwissCube saying? 1. Find the temperature readings for each side of the SwissCube(It’s a cube so there will be 6) and convert them into Kelvin from Celsius. Record the Current for each reading too. (Only fill in the grey areas if you are completing the week long project – you may need more space!). Below is a diagram showing the edges and labelling of the CubeSats used by SwissCube.
Edge Temperature Temperature Current in Celsius in Kelvin (T in (I) Celcius + 273) mA X- X+ Y- Y+ Z- Z+ X- X+ Y- Y+ Z- Z+ X- X+ Y- Y+ Z- Z+ X- X+ Y- Y+ Z- Z+ Why use Kelvin? Where has this mysterious unit come from? Well, Kelvin is the International Standard for Temperature, meaning it can be used in equations with other parameters, such as Current, without having to go through any conversions. (If you are completing the week long project, make a note of the time you record the temperatures, and complete questions 2,5,6 and all the “onto the calculation” section each time you take a measurement)
2. From your recorded temperatures, identify the data set which is facing the Sun. (HINT: It’s probably going to be the hottest one)
Face: Temperature: Current:
3. Why do you think the temperature values keep changing? What would cause this? Answers: The satellite is spinning around itself whilst orbiting the Earth
4. Why do you think Solar Panels are more effective when facing the Sun?
Answers: The hotter it will be, the more current is produced and hence more power produced by the Solar Panel
5. The Solar Panels charge up a battery, what is the average voltage of this battery across all of your data? Answers: <5V
6. Hence, using the equation Power = Current x Voltage, calculate the power being received by the Solar Panel. Remember mA means the value is x10-3 (HINT: which Current value do you think you will need?)
Answers: 0.5W 7. If the Energy Received = Power ÷ Time, how much energy is received in 1 second, 10 seconds, 1 week and the duration the SwissCube is detectable by the ground station – about 10 minutes? (HINT: You only need to do the division once, then multiply for the rest) Answers: 1 second = (0.5J 8. In 1 second, a 2000W kettle uses 2000J. How does this compare with the Solar Panel? Answers: It produces a lot less power than what a kettle needs. On to the Calculation! The SwissCube’s you are using have 10cmx10cm Solar Panels on each side. They receive power to a value you calculated earlier. VALUES: D = 1.5x1011m, π = 3.14, σ = 5.7x10-8Js-1m-2K-4 1. Using the equation: Power received = Power Emitted *((π*Solar Panel area)/ (π*4*D2)), calculate the power emitted per meter squared on the Sun (ie, per Solar Panel area on the Sun). (HINT: you may want to draw a diagram) Answers: 4.5x1025W>Power Emitted>2.1x1025W 2. Using your value for Power Emitted, Use the following equation for the total power emitted and temperature of hot objects like the Sun. 2 4 Equation: Power Emitted = 4*π*rsun *σ*T (HINT: the random circle thing is called sigma, and is the Stefan-Boltzmann’s constant. The value is at the start of the section. Also, T4 is just TxTxTxT) Answers: any numbers from 2200K We call this equation a Blackbody equation. A Blackbody is another one of those things which doesn’t mean what it says. It’s not saying an object is black, it’s saying that it radiates all the energy that is incident upon it. Like when you wear black, you get hotter on a bright day. That’s because black clothes absorb all the visible wavelengths and hence more energy! Congratulations! You have calculated the temperature of the Sun! The true assumed value is 5,500K. What do you think is the reason that your answer is/could be different? Week-long Project Plot a graph with the SwissCube sides on the y-axis and the time on the x-axis. Try and draw step-by-step images of which side is facing the Sun on A3 paper. Can you work out what angle the SwissCube is at compared to the Sun? Try drawing a diagram to demonstrate it. (You may need your teachers help)