Atomic Physics

By C K Cheung Atomic Physics

Matter ----- composed of atoms and molecules. Atom ----- composed of ??????

J.J. Thomson Experiment (1897 )

Thomson’s ‘ plum – pudding ‘model of atoms:

electron 10 – 10 m +ve charged matter spread uniformly over the entire region

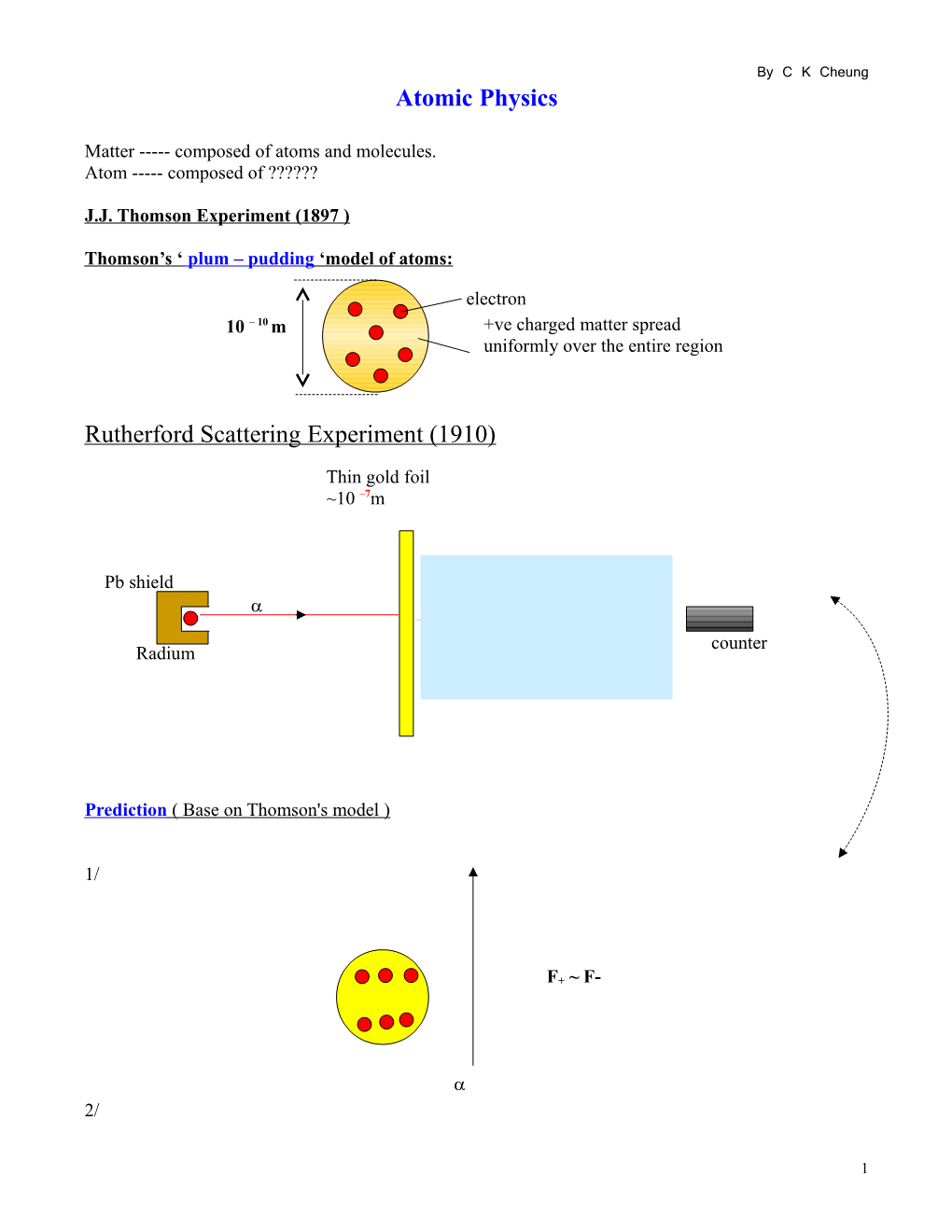
Rutherford Scattering Experiment (1910)

Thin gold foil ~10 –7m

Pb shield

 < 100 counter Radium

Prediction ( Base on Thomson's model )

F+ ~ F-

 2/

1 By C K Cheung

F+ ~ F+’ F- ~ F-‘

Hence, no matter where the  particles hit, they should be deflected only by a small angle. Experimental results: ..\powerpoint\atomic structure\Rutherford's expt..ppt

Thin gold foil ~10 –7m

 - < 100 counter Radium very few ( 1 in 8000 )

1/ many ( > 99.5 % ) of the  particles go straight through the foil and were deflected through very small angles ( < 100 ).

2/ very few ( ~ 1 in 8000 ) suffered deflections of more than 900.

Note: 1. gold is ductile 2. thin gold foil to avoid multiple collisions inside the foil.

2 By C K Cheung Rutherford’s model of atom

1/ Due to large-angle scattering of very few  particles  a small massive +ve core or nucleus.

2/ The –ve charge at relatively large distances from the nucleus so that their negative charge did not act as a shield to the +ve nucleus charge when the  particles penetrate the atom.

3/ The –ve charge in circular motion to balance the electrostatic attraction.

Rutherford’s model of atoms (1911 )

3 By C K Cheung Rutherford’s estimate of nucleus size

 Z u v = 0 R KEPE

Z = atomic no. ..\powerpoint\atomic structure\size of atom.ppt = no. of proton inside nucleus  KE = PE

1 2 1 (2e)(Ze)  mu  2 40 r

Ze2  r = 2 0mu

For closest approach: r = b

Ze2  b = 2 0mu

Take : Z = 79 e = 1.6x10 – 19 - 12 0= 8.86x10 – 27 m=6.7x 10 u = 2x10 7 ms - 1

 b ~ 10 –14 m

b R ~ ~ 10 – 15 m 2

4 By C K Cheung

Limitations of Rutherford’s model

By classical theories, all accelerating charged particles will emit radiation ( energy ). If Rutherford’s model is correct, the accelerating electrons will lose energy continuously, then they will be adhered to the nucleus and all atoms will finally be collapsed!

2/ Rutherford’s model does not predict the existence of discrete energy levels in atoms.

3/ Rutherford’s scattering experiment founded the high energy physics.

5 By C K Cheung

Bohr’s Theory of atoms (1913)

Consider an H atom:

1 (e)(e) mv 2  2 = 4 0 r r e2  v2 = ………………(1) 4 0mr

First Theory: Only those orbits occur for which the angular momenta of the planetary electron are integral h h multiples of or n( ) 2 2 h  mvr = n( ) 2 h  v = n( )…………………(2) 2mr

(2)  (1)

 n 2 h 2  e2  2 2 2  = 4 m r  4 0mr

 h2  r = 0 (n2 )  n2 me2

 r is in discrete values.

6 By C K Cheung

For H-atom,

 r = 0.529( n2) x 10 – 10 m

If n = 1,  r1 = 0.529 A

If n = 2,  r2 = 2.11 A = 4 r1

Also, the energy of the system:

1 (e)(e) PE = 4 0 r

1 1 e2 KE = mv2  m( ) 2 2 40mr

e2 Total energy = E = PE + KE = - 80r

me4 1  E = - 2 2 2  - ( 2 ) 8 0 h n n e.g.

For max. E  n = ______

For min. E  n = ______

7 By C K Cheung

Consider:

1 1 3 E12  - (  ) = 22 12 4 5 E23  36

 E12 > E23 > …………….

As n   E  0  continuous

Hence:

Formula:

1 En = - 13.6 ( ) eV n2

8 By C K Cheung

1 eV = ______J Second Theory

No electron radiates energy so long as it remains in one of the orbital energy states, and that radiation occurs only when an electron goes from a higher energy state to a lower one, the energy of the quantum of radiation = hf.

E = En2 – En1 = hf

me4 1 1 c (  )  hf  2 2 2 2 = h( ) 8 0 h n1 n2 

1 me4 1 1  wave number  ( )(  )  2 3 2 2  8 0 h c n1 n2

Rydberg constant R, R=1.0973x107m-1

9 By C K Cheung e.g. The diagram shown gives some levels of an atom. In the unexcited state the levels above - 10.4 eV are unoccupied. ( Given: h = 6.6x10 - 34 Js, C = 3x108 ms-1, e = 1.6x10 -19C)

- 1.6eV

- 3.7eV energy in eV

- 5.5eV

- 10.4eV

a/ What is the ionization energy of the atom?

Ionization energy = 0 – (-10.4) = 10.4 eV

b/ What change is taking place if radiation of wavelength 141 nm is emitted?

Ans.: - 1.6eV to - 10.4 eV

10 By C K Cheung e.g. a/ Find the energy required to excite a hydrogen atom from the ground state to the n = 4 state. 1 1 E = 13.6 (  )eV 12 4 2 1 1 = 13.6 (  )x1.6x10 19 C 12 4 2 = 2.04x10-18 J

b/ How many different possibilities of spectral line emission are there for the atom when the electron goes from n = 4 to the ground state ?

n=3  possible number of spectral n=2 lines = 6

11 By C K Cheung Evidence of energy levels

1/ Optical line spectra (optical ~ visible region) A particular line ( or a set of lines ) in an optical emission spectrum indicates the presence of a particular frequency emitted in a transition of e ( directly or in stages ) between energy levels

2/ X-ray spectra

Photoelectric Effect Source of variable & known frequency ( f ) vacuum A Emitter collector

Results of Experiment ( Laws of Photoelectric Emission )

1/ When the incident light is monochromatic, the number of photoelectrons emitted per second ( current I ) is proportional to the light intensity ( I’). Such an emission occurs effectively instantaneously. I/ A V, f = constant

I’/Wm -2

Wave theory: the incident light energy is uniformly distributed amongst the free electrons in the emitter, we should predict time delays of ~ 103 seconds.

12 By C K Cheung

2/ The KE of the emitted electrons varies from 0 to a maximum value. This definite maximum depends only on the frequency of the light, and not on its intensity. ..\powerpoint\atomic structure\photoelectric effect1.ppt

f = constant

V/V Vs 0

Vs: stopping potential 1 mv 2  eV 2 max s

Wave theory: we feel hotter in sunlight than that in moonlight,  K.E. of the emitted e should depend on light intensity.

13 By C K Cheung 3/ Electrons are not emitted when the light has a frequency lower than a certain threshold value fo. The value of fo varies from metal to metal.

I/A I’ = constant A B

f/Hz fo fo’

Wave theory: cannot predict the existence of fo!

Explanation

Planck’s Theory (1900) When radiation was emitted or absorbed, the emitting oscillator always showed a discrete sudden change of E, where E = hf.

Einstein’s Theory (1905) Extended Planck’s original idea by suggesting that E.M. wave could exhibit particle ( called photon ) behavior

1/ Electron emission is the result of a direct collision between an electron and a photon, so there is no time delay before emission starts ..\powerpoint\atomic structure\photoelectric effect2.ppt

14 By C K Cheung 2/ Light intensity   number of photon arriving per m2 per second  but not energy of individual photon .

I’ , f

2I’ , f

3/ fo depends on the material because each material requires a certain minimum energy ( called work function , W ) to free an electron.

W = hfo

15 By C K Cheung Formula:

1 mv 2 2

1  hf = W + mv 2 2 1 hf = hfo + mv 2  2  hf = hfo + eVs

This formula was verified by Millikan in 1916

h slope = e

f/Hz fo’