CONCEPT EXERCISES
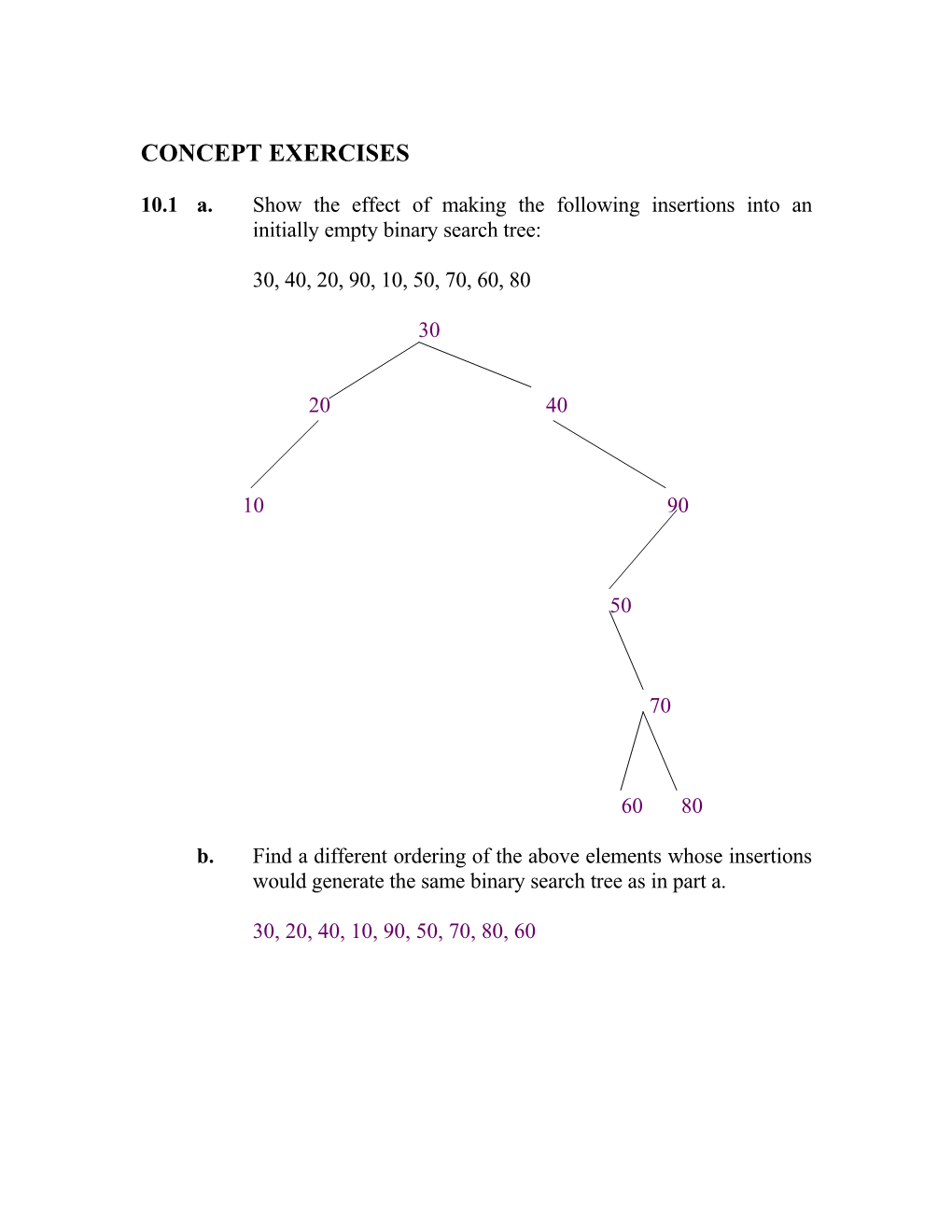
10.1 a. Show the effect of making the following insertions into an initially empty binary search tree:
30, 40, 20, 90, 10, 50, 70, 60, 80
30
20 40
10 90
50
70
60 80
b. Find a different ordering of the above elements whose insertions would generate the same binary search tree as in part a.
30, 20, 40, 10, 90, 50, 70, 80, 60 10.2 Describe in English how to remove each of the following from a binary search tree:
a. an element with no children
Simply remove the element and remove the corresponding subtree-link from the element’s parent (if the element is not the root).
b. an element with one child
Replace the parent-element link and the element-child link with a parent-child link.
c. an element with two children
Copy the element’s immediate successor into element, and then remove that immediate successor (by part a or part b).
10.3 a. For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into a BinarySearchTree object, the height of the tree will be linear in n.
Arrange the elements in increasing order, for example (or in decreasing order).
b. For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into a BinarySearchTree object, the height of the tree will be logarithmic in n.
The first element should be n / 2. Then half of the remaining elements will be in the left subtree, and half in the right subtree. The next element in the arrangement can be n / 4. Then half of the remaining elements in the left subtree of the whole tree will be in the left subtree of n / 4. The next element in the arrangement can be 3n / 4. The arrangement is
n / 2, n / 4, 3n / 4, n / 8, 3n / 8, 5n / 8, 7n / 8, n / 16, 3n / 16, … c. For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into an AVLTree object, the height of the tree will be logarithmic in n.
Any arrangement will do, because the height of an AVL tree is always logarithmic in n.
d. For any positive integer n, is it possible to arrange the integers 1, 2, …, n so that when they are inserted into an AVLTree object, the height of the tree will be linear in n? Explain.
No, because the height of an AVL tree is always logarithmic in n.
10.4 In each of the following binary search trees, perform a left rotation around 50.
a. 50
60
70
60
50 70
b. 30
20 50
40 80 70 100
30
20 80
50 100
40 70
c. 30
20 50
40 80
45 70 100
60 75 30
20 80
50 100
40 70
45 60 75
10.5 In each of the following binary search trees, perform a right rotation around 50.
a. 50
40
30
40
30 50 b. 60
50 70
40 55
30 45
60
40 70
30 50
45 55 c. 30
20 50
40 80
48 60 100 55 75
30
20 40
50
48 80
60 100
55 75
10.6 In the following binary search tree, perform a double rotation (a left rotation around 20 and then a right rotation around 50) to reduce the height to 2.
50
20 90
10 40
30 (after the left rotation around 20)
50
40 90
20
10 30
(after the right rotation around 50)
40
20 50
10 30 90
10.7 In the following binary search tree, perform a "double rotation" to reduce the height to 2:
50
20 80
70 100 60
(after the right rotation around 80)
50
20 70
60 80
100
(after the left rotation around 50)
70
50 80
20 60 100
10.9 Suppose we define maxh to be the maximum number of elements in an AVL tree of height h.
a. Calculate max3.
The maximum number of elements will be attained for a full AVL 3 tree. By the Binary Tree Theorem, max3 = 2 * 2 – 1 = 15.
b. Determine the formula for maxh for any h >= 0. Hint: Use the Binary Tree Theorem from Chapter 9.
h+1 maxh = 2 – 1 c. What is the maximum height of an AVL tree with 100 elements?
Since min9 = fib (12) – 1 = 143, the maximum height of an AVL tree with 100 elements must be less than 9. Since min8 = fib (11) – 1 = 88, the maximum height of an AVL tree with 100 elements is 8.
10.10 Show that the height of an AVL tree with 32 elements must be exactly
5. Hint: calculate max4 and min6.
Since max4 = 31, the maximum number of elements in any AVL tree of height 4 is 31. Since min6 = fib (9) – 1 = 33, the minimum number of elements in an AVL tree of height 6 is 33. So any AVL tree with 32 elements must have height 5.