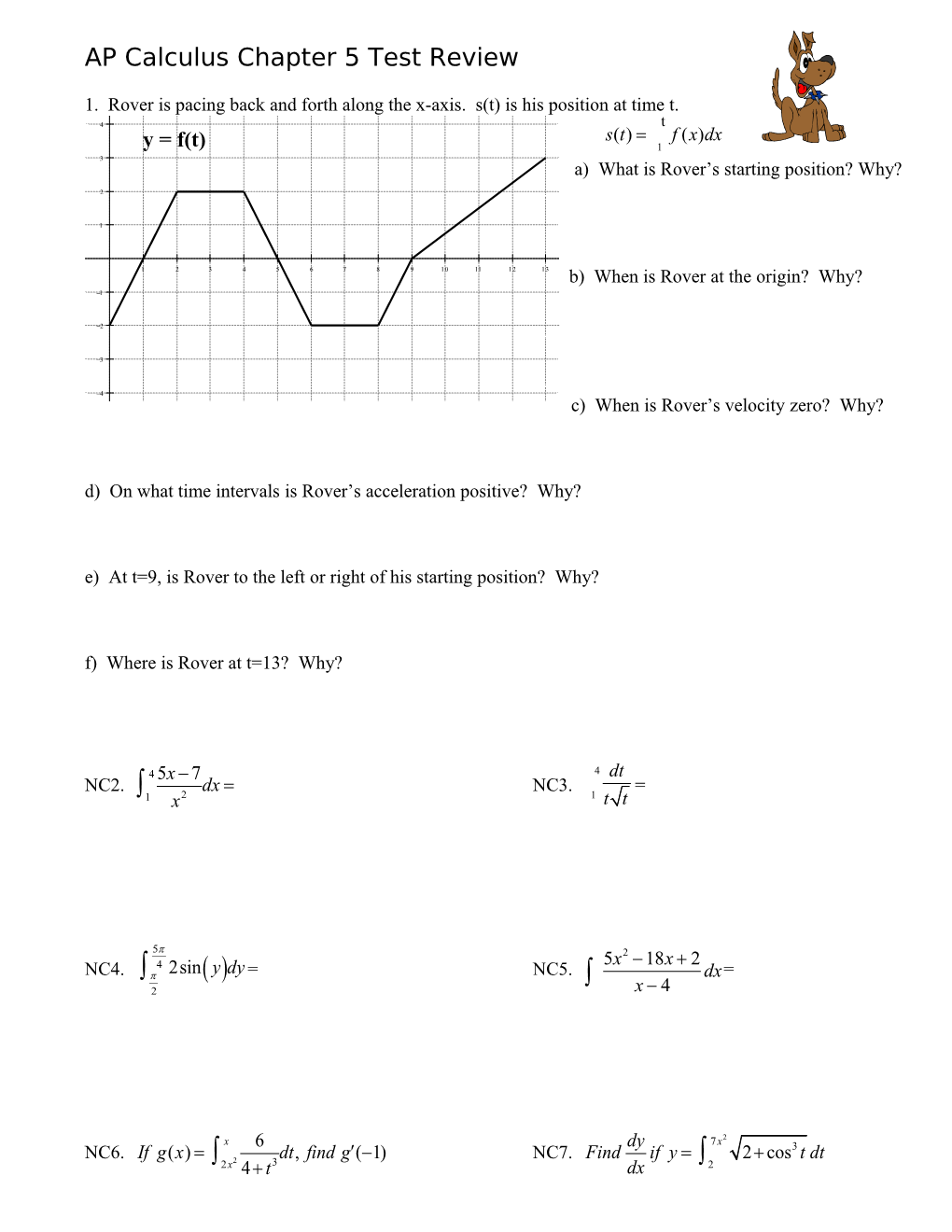
AP Calculus Chapter 5 Test Review

1. Rover is pacing back and forth along the x-axis. s(t) is his position at time t.  t s( t )= f ( x ) dx y = f(t) 1  a) What is Rover’s starting position? Why?

             b) When is Rover at the origin? Why? 





 c) When is Rover’s velocity zero? Why?

d) On what time intervals is Rover’s acceleration positive? Why?

e) At t=9, is Rover to the left or right of his starting position? Why?

f) Where is Rover at t=13? Why?

4 5x -7 4 dt NC2. dx = NC3. = ò 2 1 1 x t t

5p 5x2 -18x + 2 NC4. 4 2sin y dy = NC5. = ò p ( ) ò dx 2 x - 4

x 6 dy 7x2 NC6. If g(x) dt, find g¢( 1) NC7. Find if y 2 cos3 t dt = ò 2 3 - = ò + 2x 4+ t dx 2 8. A sled powered by a wound rubber band moves along a track until friction and the unwinding of the rubber band gradually slow it to a stop. A speedometer in the sled monitors its speed, which is recorded at 3-second 30 intervals during the 30-second run. Use a right Riemann Sum with 5 partitions to estimate v(t)dt and state ò0 the meaning of the integral in the context of this problem.

Time Speed (sec) (ft/sec) 0 5.3 3 5.25 6 5.04 9 4.71 12 4.25 15 3.66 18 2.94 21 2.09 24 1.11 27 0.47 30 0.0

15 9. Using the table above, estimate v(t)dt using trapezoids with 5 partitions. ò0

10. Find the total area of the shaded regions for y = 0.8x4 – 2x2 + 0.5. The left region is bounded on the right side by the minimum.

3 2 2 NC11. If f (x)dx = 6 and f (x)dx = 4, then (5- f (x)) dx = ò0 ò0 ò3